Abstract
Living beings display self-sustained daily rhythms in multiple biological processes, which persist in the absence of external cues since they are generated by endogenous circadian clocks. The period (per) gene is a central player within the core molecular mechanism for keeping circadian time in most animals. Recently, the modulation PER translation has been reported, both in mammals and flies, suggesting that translational regulation of clock components is important for the proper clock gene expression and molecular clock performance. Because translational regulation ultimately implies changes in the kinetics of translation and, therefore, in the circadian clock dynamics, we sought to study how and to what extent the molecular clock dynamics is affected by the kinetics of PER translation. With this objective, we used a minimal mathematical model of the molecular circadian clock to qualitatively characterize the dynamical changes derived from kinetically different PER translational mechanisms. We found that the emergence of self-sustained oscillations with characteristic period, amplitude, and phase lag (time delays) between per mRNA and protein expression depends on the kinetic parameters related to PER translation. Interestingly, under certain conditions, a PER translation mechanism with saturable kinetics introduces longer time delays than a mechanism ruled by a first-order kinetics. In addition, the kinetic laws of PER translation significantly changed the sensitivity of our model to parameters related to the synthesis and degradation of per mRNA and PER degradation. Lastly, we found a set of parameters, with realistic values, for which our model reproduces some experimental results reported recently for Drosophila melanogaster and we present some predictions derived from our analysis.
Introduction
Predictable environmental changes such as the daily variation in ambient lighting, temperature, nutrients, etc., have been critical for the temporal organization of most living beings. Organisms have developed endogenous circadian clocks, which generate most of the daily variations in their molecular biology, biochemistry, physiology and behavior with a period ∼ 24 h. These circadian rhythms are self-sustained and persist in the absence of external clues. Importantly, circadian clocks are entrained by periodic environmental cues and allow organisms to anticipate their physiology to these external changes [1].
Nearly all metazoans studied so far have at least one circadian oscillator within each cell, which is thought to enhance cellular fitness by temporally regulating key metabolic and physiological processes. At the single cell level, the circadian clockwork is based on a set of genes, called clock genes, whose protein products (clock proteins) are necessary components for the generation and regulation of circadian rhythms. Most clock genes are expressed in a circadian fashion as a consequence of their mutual interaction and regulation. The mechanism by which clock genes and proteins interact with one another is commonly called the molecular clock mechanism and is based on interconnected transcriptional-translational feed back loops (TTFL). By means of this mechanism, the clock genes also regulate downstream specific output genes (called clock-controlled genes, ccgs) in a circadian manner [2]. The period (per) gene is a central player within the core molecular mechanism for keeping circadian time in most animals. However, other clock components are also required to sustain the per feedback loop [3].
The complexity of the molecular circadian rhythmicity has been largely unraveled through experimental studies but also by the use of mathematical models, which are powerful tools able to yield and explain non-intuitive results [2, 4, 5]. Goldbeter [6] developed the first mathematical model for the Drosophila molecular circadian clock based on the negative feedback exerted by the PER protein over its own transcription. Similar kinetic models have subsequently been used by many authors to describe diverse aspects of molecular circadian rhythmicity such as the entrainment by light-dark cycles, responses to specific drugs, etc [5, 7–14]. Moreover, stochastic versions of these models were also developed in order to study the robustness of molecular rhythmicity with respect to molecular noise [9, 15, 16].
Experimental and theoretical studies have always considered transcription as the main mechanism by which it is possible to exert temporal control over gene expression [17, 18]. However, in recent years an increasing number of reports have stressed the importance of post-transcriptional mechanisms as an alternative level of gene expression regulation [19, 20]. Specifically, translational modulation is now recognized as a major post-transcriptional mechanism for the control of gene expression in a wide range of cellular conditions. This process allows a rapid fine tuning of protein levels, in both time and space, without requiring transcription of new mRNAs or post-translational regulation [21–24]. In addition, translational regulation of some clock components, like PER, have been recently described in flies and mammals. For instance, both, the protein TWENTY FOUR (TYF) and the non-canonical translation factor NAT1 enhance PER translation in flies [25, 26]; whereas in mammals, two different RNA-binding proteins, LARK and hnRNP-Q, bind independently to per1 mRNA, enhancing its translation [27, 28]. It is important to note that although the modulation of PER translation has been observed experimentally, this post-transcriptional regulatory process was never incorporated into mathematical circadian clock models. Furthermore, theoretical studies of the molecular circadian clock have never analyzed in detail how the translational kinetics affects the oscillatory properties of the circadian molecular clock.
Here we hypothesize that the effective kinetics of PER translation is the result of the fine modulation of PER synthesis by translational regulators (R). Accordingly, we posit that the regulation of PER translation involves changes in its translational kinetics, which ultimately affects the molecular clock dynamics. Therefore, the main goal of this work is to characterize how kinetically different mechanisms of PER translation affect the dynamical behavior of the molecular clock.
By using a single-cell model for the circadian molecular clock [6, 9, 29], we performed a systematic and novel study of how the oscillatory properties (period, amplitude and time delays -i.e.: time lags between the per mRNA and protein expression-) of a core circadian clock model are affected by the kinetics of PER translation. We propose a master clock model from which we can study different particular cases by specifying the values of translation-related parameters. This master clock model includes two kinetically different mechanisms of PER translation, one with a first order kinetics and the other with a Michaelis-Menten kinetics. Through the introduction of a Michaelis-Menten term, we have performed a deep characterization of whether, and to what extent, the introduction of nonlinearities in the translational kinetics affects the dynamical properties of the system, either when the translation occurs by a single kinetic mechanism (characterized only by the parameters of the Michaelis-Menten term) or by the sum of two kinetically different mechanisms. We have interpreted our model according to experimental observations and the results obtained as a consequence of the regulation of PER synthesis. We found that the emergence of self-sustained oscillations, as well as the period, amplitude, and time delays values depend on the kinetic parameters related to PER translation. Interestingly, under certain conditions, a PER translation mechanism with saturable kinetics introduces longer time delays than a mechanism ruled by a first-order kinetics. In addition, we found that the kinetic laws of PER translation significantly changed the sensitivity of our model with regard to parameters related to the per mRNA synthesis and PER degradation. Lastly, we found a set of parameters, with realistic values, for which our model reproduces some experimental results reported recently for Drosophila melanogaster [25, 26], and we present some predictions derived from this study.
The molecular circadian clock model
In this work we will mainly refer to the Drosophila melanogaster molecular clock, but the same principles (i.e.: TTFL mechanism) are shared with the mammalian molecular clock [2, 30]. In the Drosophila core feedback loop, the clock proteins CLOCK (CLK) and CYCLE (CYC) heterodimerize and bind to regulatory sequences (E-boxes) present in the promoter of target clock genes such as per, timeless (tim) and doubletime (dbt). These interactions promote the transcriptional activation of such clock genes, yielding their corresponding mRNAs. Once they are translated, the PER and TIM proteins start accumulating in the cytoplasm, about 6—8 h after their respective mRNAs. The DOUBLETIME (DBT) protein binds to PER and phosphorylates it, whereas TIM stabilizes the DBT-PER complexes, enabling the accumulation of DBT-PER-TIM complexes in the cytoplasm. Nuclear localization of such complexes is boosted by the phosphorylation of PER and TIM by CASEIN KINASE 2 (CK2) and SHAGGY (SGG), respectively. Within the nucleus, PER-TIM (and /or DBP-PER-TIM) complexes bind to CLK, promoting the release of the heterodimer CLK-CYC from the E-boxes. PER-TIM complexes therefore repress their own transcription by inhibiting the transcriptional activity of CLK-CYC. When PER levels decay because of degradation, CLK accumulates, the CLK-CYC heterodimer can bind to the E-boxes and a new loop begins [3]. Additional feedback loops such as the clk and cwo loops, are interlocked with the core loop, conferring robustness to the mechanism and supporting circadian rhythmicity in flies. Furthermore, kinases, phosphatases and other enzymes post-translationally modify clock proteins, which also modulate molecular circadian rhythmicity [3].
This conceptual model of how the Drosophila molecular clock is organized and works can be transformed into a mathematical model by the selection of suitable mathematical equations and parameter values in order to represent the biochemical processes involved [31]. Indeed, numerous mathematical models, based on the Goodwin oscillator, have been developed by many authors [5, 7–14, 32]. The complexity of these deterministic models has evolved according to the identification of new clock components and processes, which have generated very detailed models that attempt to mimic the exact behavior of the molecular clock [31, 32]. The main drawback of those very detailed models is the large number of parameters involved, many of which have experimentally unknown values [31, 32]. As discussed previously [33], a very detailed mathematical model does not guarantee good consistency between the results of the model and experimental data. On the other hand, less detailed mathematical models, such as the Goldbeter model [6] and its derivatives [9, 12, 14, 29], include core processes involved in the negative feedback exerted by a regulatory protein (PER) on the expression of its own gene, keeping the model as simple as possible. Indeed, in some cases, these less detailed mathematical models produced results more similar to what it is observed experimentally [33], and are more suitable for studying the underlying properties of the feedback loop systems [31, 32]. This is the focus of our work and, therefore, we based our study on a Goldbeter structure-based model because, to our judgement, this model describes quite rigorously the per mRNA and protein dynamics, with (relatively) few parameters [6].
We took as a starting point of our work the deterministic model for the Drosophila molecular clock proposed by Gonze and co-workers [9]. Gonze’s deterministic version has exactly the same functional form (terms and equations) as the original model published by Goldbeter in 1995 [6]. The differences between these two models are exclusively related to the parameters values, which we assumed that were improved in the more recent paper [9]. In our model (Fig. 1), most of the core processes involved in circadian rhythmicity were assumed to occur with kinetics identical to those described in previous reports [9, 29], except for PER translation. Thus, our model relies on the following assumptions discussed below.
Figure 1. Scheme of the ‘master’ model proposed in the present work.
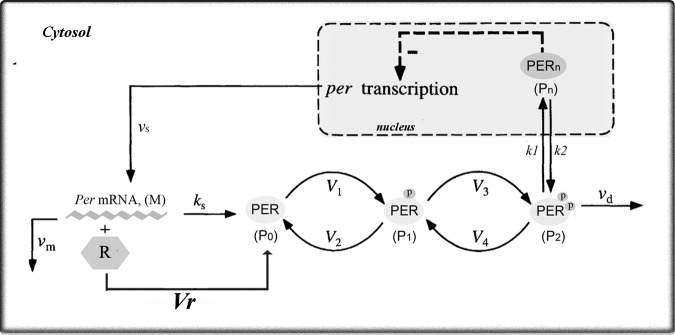
The model is based on a Goodwin oscillator in which the temporal variation of the concentrations of mRNA (M) and the various forms of clock protein, cytosolic (P0, P1, P2) or nuclear (Pn), are governed by the system of kinetics equations 1–5. The associated parameters with their specific values are indicated in S1 Table in S1 File. This scheme is similar to the one presented in [6].
per mRNA (M) is transcribed into the nucleus and transferred to the cytoplasm at a rate vs (nM h −1), where it decays in a Michaelis-Menten fashion with rate vm (nM h −1) and Michaelis constant K m (nM). In the cytoplasm, the per mRNA can be translated to produce the PER protein. The exact functional form of the PER translation is not known experimentally, except that it is modulated by some regulators that enhance the PER translation [25, 26]. Besides, since multiple regulators and factors are involved in the effective kinetics of protein synthesis, it is likely that this process occurs with nonlinear kinetics [34, 35]. Therefore, we have made the plausible assumption that the PER translation follows a Michaelis-Menten kinetics. We have chosen a Michaelis-Menten kinetics because it is one of the simplest ways to represent a biochemical-enzymatic reaction with nonlinear kinetics. Thus, by taking into account a Michaelis-Menten kinetics for the PER translation we have incorporated two new parameters to the model: the Michaelis constant Kr (nM) and the maximum rate of the translational process Vr (nM h −1). In classic enzymology the maximum rate Vmax is proportional to the concentration of the enzyme involved in the enzymatic reaction. Analogously, here the Vr parameter is proportional to the concentration of multiple translational regulators involved in PER translation, which we generically represent as R and are assumed constant across time. Therefore, the PER translation mechanism following a Michaelis-Menten kinetics is dependent on the R activity and for simplicity we named it as the R-dependent translation. In previous models the PER translation rate was assumed as proportional to the per mRNA concentration and characterized by the first-order rate constant ks (h −1) [6, 9, 29]. In our model we have maintained this translational mechanism, independent of the R activity, referred here as the R-independent translation.
Thus, our model takes into account two different mechanisms by which per mRNA can be translated: an R-independent (characterized by the first-order rate constant ks) and an R-dependent (with Michaelis-Menten kinetics) translation. We have added the R-dependent translation in our model, instead of replacing the R-independent step, mainly because considering the double mechanism allows us to obtain a master model from which we can study different particular cases by specifying the values of ks, Vr and Kr:
by setting ks = 0, the model considers that the R-dependent mechanism is the only one involved in PER translation;
by setting Vr = 0, the model takes into account that the R-independent translation is the only mechanism involved in PER synthesis. Specifically, when ks = 2 the model is exactly the same as the original model [9].
by setting Kr ≠ 0, Vr ≠ 0 and ks ≠ 0 we explored how the clock dynamic is affected when both translation mechanisms coexist, but have different weights within the system. We have analyzed the system with a double mechanism of PER translation because several experimental studies have recently revealed that some clock proteins (i.e., dPER in Drosophila and PER1 in mammals) could be translated by both cap-dependent and cap-independent mechanisms, although the relative contribution of such mechanisms to the overall translational process under normal conditions is still unknown experimentally [26, 36].
The proposed mathematical model also takes into account the PER post-translational modifications described in the literature [6, 9, 29]: PER (P0) is phosphorylated twice in a consecutive and reversible fashion, resulting in the mono-phosphorylated PER (P1) and the bi-phosphorylated PER (P2). The first phosphorylation/dephosphorylation step is modeled by a Michaelis-Menten mechanism with a maximum rate V1 (nM h −1) and a Michaelis constant K1 (nM) for the forward reaction and with a maximum rate V2 (nM h −1) and a Michaelis constant K2 (nM) for the reverse reaction. The same kinetics is assumed for the second phosphorylation/dephosphorylation step, with maximum rates V3 (nM h −1) and V4 (nM h −1), and Michaelis constants K3 (nM h −1) and K4 (nM h −1), respectively. Only biphosphorylated PER (P2) can be degraded with a Michaelis-Menten kinetics with maximum rate vd (nM h −1)and Michaelis constant Kd (nM). Nuclear translocation of the bi-phosphorylated PER is considered as a reversible step with first-order rate constants k1 (h −1) and k2 (h −1) for the forward and reverse processes, respectively. To simplify the model it was assumed that nuclear PER (Pn) itself is the repressor exerting the negative feedback on per expression. The feedback term is described by a Hill-like equation with Hill coefficient nH. The bigger the nH value, the more cooperative is the repression of per transcription.
In his pioneering work, Goldbeter had assumed allosteric kinetics for the repression of per transcription, with nH = 4 [6], but he also showed that non-cooperative kinetics, with nH = 1, can give rise to self-sustained oscillations. Forger and coworkers [11] suggested that there are non-allosteric interactions among E-boxes, and proposed a non-cooperative per transcription. Recently, Brown and collaborators have supported the idea that repression must be a cooperative process [37]. In this work we have therefore taken into account both cooperative and non-cooperative per repression mechanisms and we compared the results obtained in each case.
The total protein (Pt) is calculated as the sum of all PER species (Pt = P0 + P1 + P2 + Pn).
The differential equations of this model are:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
It is necessary to clarify here that the nonlinear terms appearing in the kinetic equations do not correspond to single reaction steps. Instead, these terms represent compact kinetic expressions obtained after application of quasi-steady-state hypotheses on enzyme substrate or gene-repressor complexes.
Summarizing, the model consists of a set of five ordinary differential equations describing the time evolution of five components of the molecular circadian clock: M, P0, P1, P2 and Pn. The system requires 20 parameters, whose values and definitions are listed in S1 Table in S1 File. Unless indicated otherwise, the value for most of the parameters are those listed in S1 Table in S1 File, which are the same than those reported in [9].
Results
The oscillatory behavior of the system
We used the deterministic version of the model proposed by Gonze and coworkers [9] as the starting point for our study. First, we characterized the effect of the R-dependent translation on the system dynamics, using similar conditions (i.e.: ks = 2 h −1) to those previously reported [9, 29]. In order to do this, we studied the dynamical behavior of the system when the R-dependent translation has a small contribution to the overall PER translation, that is, when the Vr and Kr parameters are very small compared to the ks value (i.e.: ks = 2 h −1, Kr = 10−2 nM and Vr = 10−2 nM h −1).
Fig. 2, A and B , shows the time evolution of M, Pn and Pt for nH = 4 and nH = 1, respectively. The system displayed sustained circadian oscillations in all the variables, regardless of the assumption of a cooperative (n = 4) or a non-cooperative (n = 1) repression of per transcription. The amplitudes of such oscillations were dramatically lower in the non-cooperative model and power spectrum analysis (S1 Fig. A and B in S1 File) revealed major differences in the oscillation period (τ between the cooperative τ ≈ 22.3 h) and the non-cooperative (τ ≈ 27.7 h) cases. S1 Fig. C and D in S1 File shows a parametric plot of the concentrations of M vs Pt, revealing a limit cycle trajectory, which was obtained regardless of the initial conditions for both cooperative and non-cooperative models. These results indicate that for a small contribution of the R-dependent translation to the overall translation, the system ruled by Equations 1 to 5 reaches a regime of self-sustained oscillations, regardless of whether the model assumes cooperativity or not. Thus, assuming a cooperative repression of per transcription favors the periodic behavior of the system, increasing the amplitude of the oscillations but shortening the period length, in agreement with the results of previous reports [6]. For the cooperative case (nH = 4), we have not found major differences in the period (τ ≈ 22.3 h) or the amplitude (a) of the oscillations between the model under the conditions presented in Fig. 2 A (ks = 2 h −1, Kr = 10−2 nM and Vr = 10−2 nM h −1) and the model under the conditions corresponding to the original model (i.e.: ks = 2 h −1, Kr = 0 nM and Vr = 0 nM h −1; [9], S2 Fig. A in S1 File). For the non-cooperative case (nH = 1), on the other hand, we found that the oscillation amplitude significantly decreased when the R-dependent translation was considered (S2 Fig. B in S1 File) while the period is practically unaffected (τ ≈ 27.7 h). Together, these results revealed that a small contribution of the R-dependent translation to the overall PER translation produced minor changes in the period of the molecular clock as compared to those obtained with the original model [9]. These conclusions are further supported by the evidence emerging from the comparison between the mRNA concentration ([M]) and the Kr value (0.01 nM). Fig. 2 A shows that the [M] value at the peak is much bigger than the Kr value ([M] ≈ 1.6 nM >> Kr) and therefore the Michaelian term can be reduced to a constant term, approximately equal to Vr. The effective PER translational kinetics (that is, the sum of the R-dependent and the R-independent terms) can be written as (ks + Z)[M], with << ks, which leads to an effective translational kinetics very close to that considered in the original paper [9]. On the other hand, when [M] becomes small and gets close to the Kr value (∼ 0.01 nM at the trough), the Michaelian term can be reduced to and the effective kinetics can be written as , which is equivalent to changing the ks value from 2 h −1 to 2.5 h −1 in the original model. The impact of such a change on the period length will certainly depend on the sensitivity of the model regarding the ks variation; our numerical results revealed that the inclusion of the Michaelis-Menten term (R-dependent mechanism), with those specific Kr and Vr values, only perturbs slightly the dynamics of the system, generating a first order effective PER translation kinetics very similar to that of the original model. This explains why for nH = 4 neither the period nor the amplitude changed drastically in the model considered in Fig. 2 A , as compared with the original [9]. For nH = 1, (Fig. 2 B and S2 Fig. B in S1 File), the [M] value (∼ 0.8 nM at the peak and ∼ 0.5 nM at the trough) is, at least, fifty times bigger than the Kr value. In this case we could also consider that [M ] >> Kr and infer that the effective translational kinetics is ultimately described by a first order law, very similar to the one presented in the original model. Therefore we would not expect any significant changes in the dynamical properties of the model considered in Fig. 2 B as compared with the original model. Although this seems to be true for the period length, our numerical results revealed that the oscillation amplitude changed significantly (∼ 17—19%) in our model as compared with the original one. This observation highlights, on one hand, that it is not always possible to intuitively predict the dynamical behavior of a system like the one presented here. On the other hand, this observation reveals that the changes in amplitude produced by the contribution of the R-dependent translation were indeed dependent on the Hill coefficient, with the differences being more evident for nH = 1 than for nH = 4. It is noteworthy that the Michaelis-Menten term, under the conditions of Fig. 2 B , impacts more on the peak-to-trough amplitude than on the period length.
Figure 2. Sustained oscillations generated by the PER model.
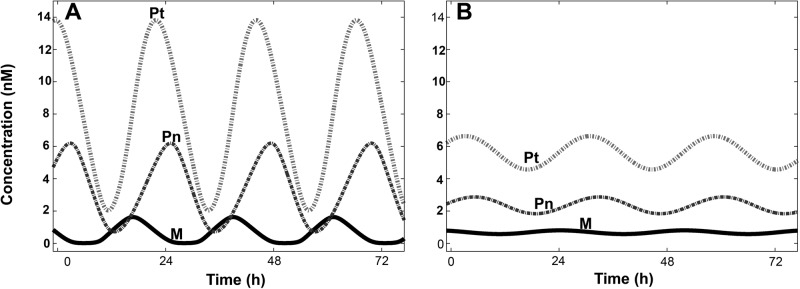
Temporal evolution of the variables M, Pn, and Pt, which represent the Per mRNA, nuclear PER and total PER, respectively. Repression of per transcription was assumed as a cooperative (A) or a non-cooperative (B) process. Parameter values are those listed in S1 Table in S1 File, except for the translation-related parameters, which, for this figure, acquired the following values: ks = 2 h −1, Kr = 10−2 nM and Vr = 10−2 nM h −1.
To further study the changes in period and amplitude when the R-dependent mechanism has a bigger contribution to the overall translational process, in the next section we show a detailed numerical characterization of the dynamics of our model for different combinations of ks, Vr and Kr parameter values.
Numeric characterization of oscillatory behavior as a function of the parameters related with PER translation
In order to study the dependence of the system dynamics on the translation-related parameters (ks, Vr and Kr), we numerically characterized the period (τ) and the amplitud (a) of the per mRNA (M) and total PER (P t) oscillations as functions of these parameters (Fig. 3, Fig. 4 and S5–S6 Fig. in S1 File).
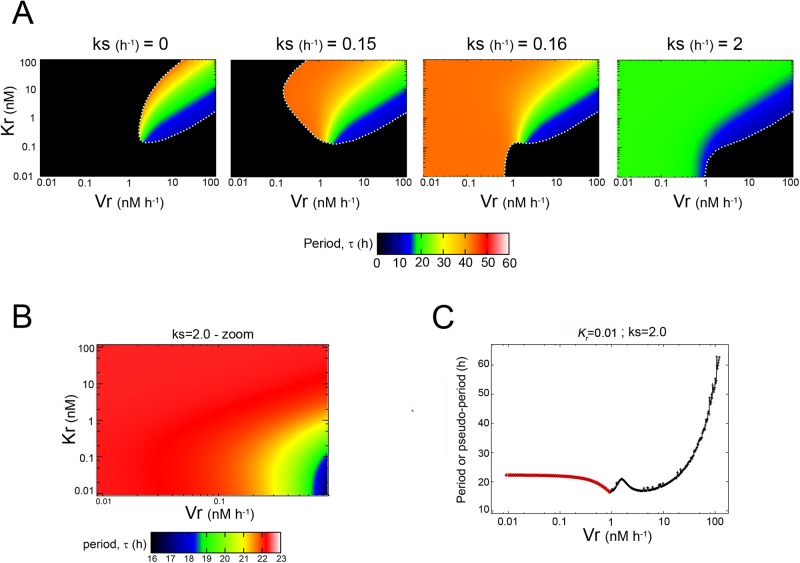
Figure 3. Dependence of the period (τ) with ks, Vr and Kr, for nH = 4.
(A) The τvalues are shown in pseudocolor within the Kr-Vr-parameter space for different values of the ks parameter from 0 (left) to 2 h −1 (right). Black areas indicate zones in which there are damped oscillations. A white dotted line was added in order to emphasize the transition between the two dynamical behaviors observed in our model. Note the changes in the oscillatory domain and the τ length with ks (the color key for τ is at the bottom of the plots). (B) An inset of the Kr-Vr-space shown in panel A for ks = 2 h −1 (right) shows the subtle changes in τ. Note that the key color was rescaled in order to display the differences in more detail. (C) Dependence of τ (red line) with Vr for a fixed value of Kr = 0.01 nM). Black line shows the pseudo-period value for damped oscillations. See the text for further details.
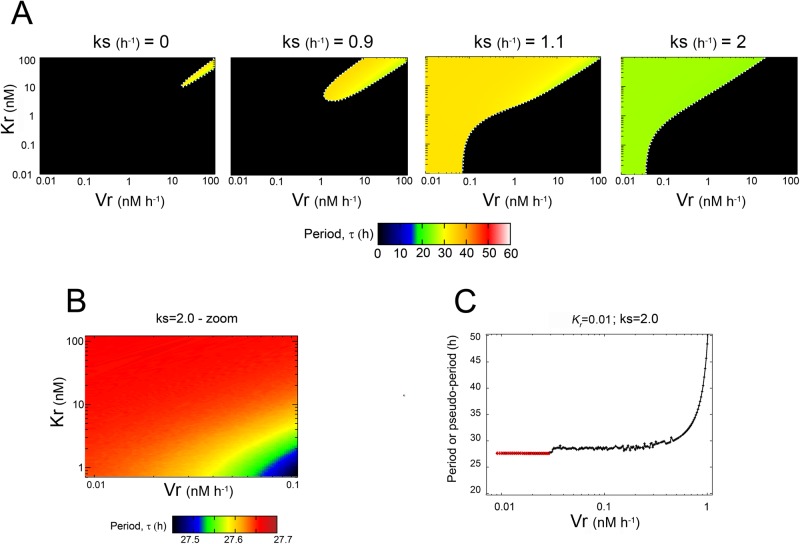
Figure 4. Dependence of the period (τ) with ks, Kr and Vr for nH = 1.
(A) The τ values are shown in pseudocolor within the Kr-Vr-subspace for different values of the ks parameter, from 0 (left) to 2 h −1 (right). Infradian (τ ≥ 28 h) are predominant for ks values < 2 h −1. For each ks value, the range of τ values is narrower than those observed for nH = 4 (the color key for τ is at the bottom of the plot). Black areas indicate zones in which there are damped oscillations. A white dotted line was added in order to emphasize the transition between the two dynamical behaviors observed in our model. (B) An inset of the Kr-Vr-space shown in panel A for ks = 2 h −1 (right) shows how τ changes within the circadian range; nevertheless the extent of τ change is smaller than that observed for nH = 4. Note that the key color was rescaled in order to display the differences in more detail (C) Dependence of τ (red line) with Vr for a fixed value of Kr = 0.01 nM. The black line shows the pseudo-period value for damped oscillations.
For the cooperative model (nH = 4), Fig. 3 A shows the phase diagrams in the Kr-Vr subspace, in which the τ values are shown in pseudocolors and each diagram corresponds to a different ks value. The ks variations were introduced in order to analyze the relative importance of the R-independent translation versus the R-dependent mechanism. We have systematically varied the ks values ranging from 0 to 2 h −1 and representative diagrams for specific ks values are presented in Fig. 3 A . For all the ks values considered, two major dynamic behaviors were observed depending on the Vr and Kr values: a region where the system oscillated in a sustained way (colored regions) and another region where the system decayed to a fixed point in an oscillatory manner (damped oscillations, black regions).
When the only mechanism involved in the PER translation was the R-dependent one (ks = 0 h −1), we found a small domain within the Vr-Kr subspace in which the system oscillated self-sustainedly with different τlengths, depending on the Vr-Kr parameter values. Circadian and close-to-circadian oscillations (green) emerged only in a region surrounded by the domains of ultradian (blue) and infradian (yellow to red) oscillations. In order to quantify the strength of saturation for the PER translation process taking place via the R-dependent mechanism, we numerically calculated the saturation index (I) values for each Kr-Vr combination within the oscillatory domain ([38], see details in the S1 File). S3 Fig. A in S1 File shows that a high proportion of the oscillatory domain presents small I values (between 0 and 0.5) and a small region exhibits large I values (between 0.5 and 0.8). However, the I values were never bigger than 0.8. We did not observe any correlation between the I values and the oscillation period. For Kr >>> [M], the I values were small (i.e.: right-top corner of S3 Fig. A in S1 File) and the system with an R-dependent translation (ks = 0 h −1) could trivially have the same behaviour than the original model introduced by Gonze ([9], ks = 2 h −1; Vr = 0 nM h −1), as long as Vr = 2Kr (green straight line plotted in S3 Fig. A in S1 File). Taken together, these results revealed that a PER translation process taking place exclusively via an R-dependent mechanism (Michaelis-Menten kinetics; ks = 0 h −1) was sufficient to obtain self-sustained oscillations within a specific Vr-Kr domain; within that domain it was possible to obtain different degrees of saturation by tuning the Kr and Vr parameter values.
When ks > 0 h −1, self-sustained oscillations emerged in Vr-Kr domains that increased with ks and spread out from the infradian oscillation region. Between ks = 0.15 h −1 and 0.16 h −1 the system exhibited a transition from a regime dominated by damped behavior to a regime dominated by self-sustained oscillations. In the latter regime, the shape of the oscillatory domain remained practically unchanged as ks increased, with only slight variations in the periodicity. We observed that as ks increased, the domains of infradian oscillations decreased in size. In particular for ks = 2 h −1 the infradian region disappeared and the subspace was dominated by circadian and close-to-circadian behavior. Fig. 3 B is an inset of the diagram shown in Fig. 3 A for ks = 2 h −1, which does not maintain the original color ranges exhibited in the corresponding full diagram because we wanted to highlight the subtle τ differences in more detail. This figure reveals that, for a fixed value of Kr, an increase in the Vr value produced a shortening of the τ length. This dependence of τ on the Vr value was observed regardless of the ks values examined, which was clearly represented by the pseudocolor variation in each map of Fig. 3 A , going from red (long τ to blue (short τ). We did not observe, for any of the specific ks and Kr values considered, any alteration of the pseudocolor gradient as Vr grew (that is, τ codified in red > τ codified in orange > τ codified in yellow > τ codified in green > τ codified in blue). This information can be also observed in Fig. 3 C (red line), in which we have plotted the τ values as a function of the Vr for a fixed value Kr = 0.01 nM. This figure also includes the pseudo-period values of the damped oscillations (black line) present in the black region of the diagram shown in Fig. 3 A for ks = 2 h −1 (see below). S3 Figs. B–D in S1 File show the I values within the Kr-Vr-diagrams for the other ks values shown in Fig. 3 A . We observed that the proportion of the oscillatory domain presenting large I values (i.e.: I ∼ 1) increased as we increased the ks value from 0.15 h −1 (S3 Fig. B in S1 File) to 0.16 h −1 (S3 Fig. C in S1 File), which means that the R-dependent translation becomes highly saturated in that region. This is likely to be related to the transition observed in the Kr-Vr diagrams, which changed from a regime dominated by damped behavior to a regime dominated by self-sustained oscillations (including the region of small Kr and Vr values). Nevertheless, when we further increased the ks value from 0.16 h −1 (S3 Fig. C in S1 File) to 2 h −1 (S3 Fig. D in S1 File) we observed that the region with small I values (between 0 and 0.5) becomes increasingly bigger. This is consistent with the fact that an increase of ks leads to an increase of the effective kinetics of PER translation, which reduces the overall mRNA concentration available to be translated by the R-dependent mechanism.
Fig. 4 shows a similar analysis but for the non-cooperative model (nH = 1). In this case (Fig. 4 A ), for all the ks values studied, the domains where self-sustained oscillations emerged were very small compared with those obtained with the cooperative model (Fig. 3 A ). Furthermore, in these domains only long circadian or infradian periods were observed. For ks = 2 h −1, the whole oscillatory domain presented circadian oscillations with τ values ≈ 27—28 h: there was a decrease in the period length as Vr increased, but for an identical increase in the Vr parameter, the τ length decreased less when nH = 1 than when nH = 4 (compare Fig. 3 B and Fig. 4 B ). Indeed, no ultradian periods were observed. Fig. 4 C also shows the changes in τ as Vr increases, for a fixed value of Kr = 0.01 nM (red line). Although the period appeared to be constant, it actually decreased slowly. The pseudo-period values (black line) corresponding to the damped oscillations (black region of the diagram shown in Fig. 4 A for ks = 2 h −1) have also been included. The analysis of the I values for nH = 1 (S3 Fig. E–F in S1 File) is similar to that for nH = 4. The only difference is that, for ks = 0 h −1 and ks = 0.9 h −1, the system was not saturated regardless of the Kr-Vr combination tested. This means that the Michaelis-Menten kinetics can be approximated by a first order kinetics, and the effective translational kinetics (sum of R-dependent and R-independent) could be written as , with , which would give trivially the same result than the original model with a change in ks.
The pseudo-period values shown in Fig. 3 C and Fig. 4 C were included in order to show that beyond the self-sustained oscillatory domain the system displays transient damped oscillations before reaching the steady state. Using linear stability analysis we have confirmed the existence of Hopf bifurcations along the transition lines between the non-oscillatory (dampened) and oscillatory domains (white dotted lines in Fig. 3 A and Fig. 4 A ; see the Supporting Information and S4 Fig. in S1 File). From the damped oscillations it was possible to measure pseudo-period values by numerically computing the average duration (time) between two consecutive peaks of the damped oscillations observed in PER concentration [39]. Near to the Hopf bifurcation point, these damped oscillations can exhibit pseudo-period values within the same range than the τ values corresponding to self-sustained oscillations on the other side of the transition lines.
The peak-to-trough amplitude (a) values for M and Pt were also calculated, codified in a pseudocolor key, and represented in phase diagrams in the Vr-Kr parameter subspace, both for cooperative and non-cooperative models (S5 Fig. and S6 Fig. in S1 File, respectively). In these figures we show the a diagrams for M and Pt at two different ks values, ks = 0 h −1 and ks = 2 h −1. We observed that, regardless of the value of the Hill coefficient considered, the amplitude range of M was larger for ks = 0 h −1 than for ks = 2 h −1, even when the latter produced a wider oscillatory domain. On the other hand, the amplitude range of Pt for nH = 4 remained the same for both values of ks, whereas for the non-cooperative model (nH = 1) the amplitude ranges of Pt changed slightly between the two ks values, being greater for ks = 0 h −1. In addition, we also observed that a cooperative repression of per transcription always enlarged the oscillation amplitude, regardless of the values of ks explored, which is in agreement with the results shown previously in Fig. 2. As a final remark it is important to note that the results and conclusions showed in this section hold as long as the values for the rest of the parameters of our model are the same as those listed in S1 Table in S1 File.
Characterization of the time lag between the per mRNA and PER protein expression profiles
A still open question about the molecular circadian clock is how the delay (denoted by δ) between the expression of per mRNA and protein is achieved. Long time lags between the mRNA and protein expression profiles of PER have been observed experimentally: the phase of PER expression is delayed about 6–8 h relative to the mRNA [40–42]. This time lag was mainly associated with the stability of mRNA and proteins, post-translational modifications, dimerization processes, nuclear translocation, etc [42–45]. However, it was also suggested that the translational regulation may also be contributing to the observed delays [40, 46]. To test this hypothesis, we have computed the time delay (δ) between the maximum expressions of per mRNA and nuclear PER (denoted by δn) and between the maximum expressions of per mRNA and total PER (denoted by δt) obtained with our model, for different ks, Kr and Vr values. These δ values are represented in pseudocolor within the Kr-Vr subspace for the cooperative and non-cooperative cases (Fig. 5 and S8, S14 and S16 Figs. in S1 File).
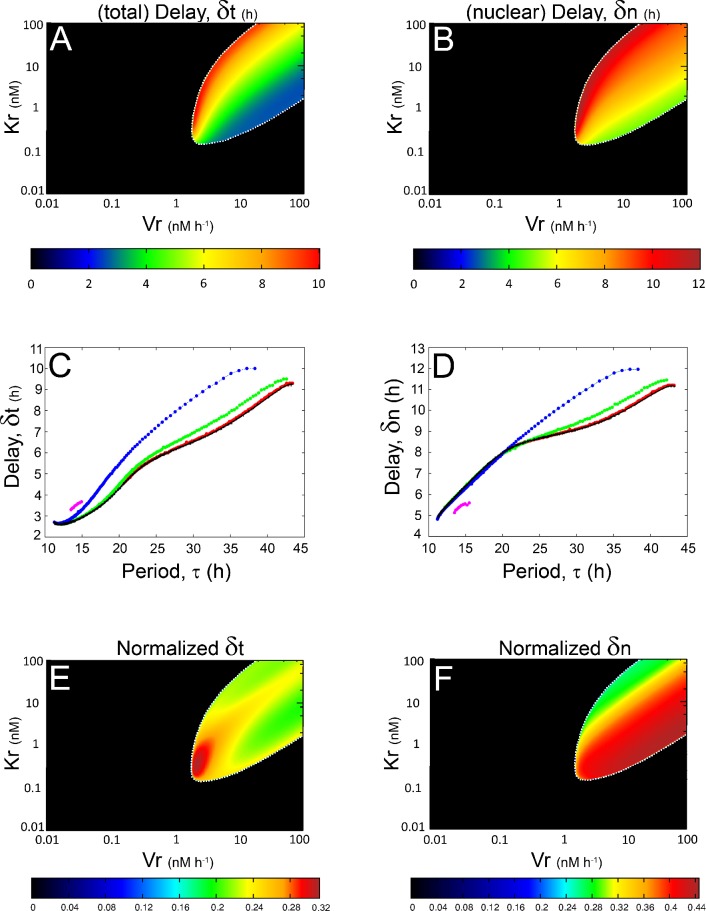
Figure 5. Analysis of the delays when PER translation is achieved by a single kinetic mechanism.
Total delay (A) and nuclear delay (B) diagrams within the Vr-Kr parameter subspace, for a cooperative model in which ks = 0 h −1. Total delay profile (C) and nuclear delay profile (D) diagrams as functions of the period τ. Each color line represents a fixed value of Kr, as follows: red = 100 nM; green = 10 nM; blue = 1 nM and magenta = 0.14 nM. For a better comparison we have included the profile δt versus τ for the model with a translational process achieved only by the R-independent mechanism (Vr = Kr = 0), which follows a first-order kinetics (black line). All these curves increase monotonically as τ increases. Figs. 5 E and F represent, respectively, the normalized total delay and nuclear delay diagrams within the Kr-Vr-subspace. The color key for each Kr-Vr-diagram is shown at the bottom of each plot. In those diagrams a white dotted line was added in order to emphasize the transition between the two dynamical behaviors observed in our model.
We started by examining the delays obtained with the original model, which assumed a first-order kinetics for the translational process [9]. This condition was achieved in our model by setting Vr = 0 nM h −1, ks = 2 h −1 and nH = 4. Under these conditions, the δn value was about 8.39 h and the δt value was about 5.11 h (S7 Fig. A in S1 File, arrows). S7 Fig. A in S1 File also shows a further characterization of the delays dependence on the ks parameter when the translational kinetics followed a first-order rate and nH = 4: a decrease of ks led to an increase of both δn and δt values. A similar profile was found for the variation of the oscillation period (τ) with ks (S7 Fig. C in S1 File). Furthermore, a monotonic relationship between delays and period was the prevailing trend observed for nH = 4 (S7 Fig. E in S1 File), in which the longer the period, the greater the delay. Minor exceptions to this behavior were found at each end of the δ t profile (i.e.: for very short or very long periods), where the δt values have changed little from one period to the other. We also observed a slowdown of the δn profile for very long periods. For nH = 1, the period monotonically decreased with ks, just as for nH = 4 (S7 Fig. D in S1 File). Nevertheless, the relationship between delays and ks was not monotonic (S7 Fig. B in S1 File), which clearly impacted on the delays-versus-period profiles: delays passed through a maximum as a function of the period length (S7 Fig. F in S1 File).
When PER translation was achieved only through an R-dependent mechanism (i.e.: ks = 0 h −1) and nH = 4, the delay values depended on the Vr and Kr values (Fig. 5 A and B ). For a fixed value of Kr, delays tended to decrease as Vr grew (S9 Fig. A and B in S1 File, rhombs), which qualitatively resembled the dependence of delays with ks previously observed in Fig. 6 A . However, a change in the Vr parameter produced smaller changes in the delays than those arising from similar changes in ks for the original model because the presence of the Kr parameter in the Michaelis-Menten mechanism produced opposing effects on the delays, which tend to increase as Kr grows (S9 Fig. C and D in S1 File, rhombs). Conversely, when nH = 1 the dependence of delays with Vr or Kr was not monotonic (S8 Fig. A and B in S1 File; see also S9 Fig. in S1 File, circles).
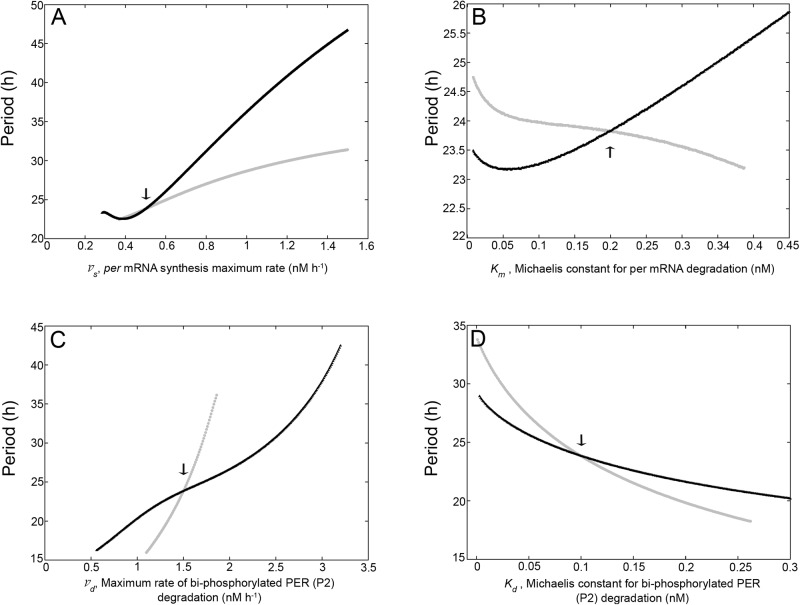
Figure 6. Profiles of the period (τ) as a function of several non-translation related parameters of the model.
Dependence of the period (τ) on: the maximum rate of per mRNA synthesis, vs (A); the Michaelis constant for per mRNA degradation, Km (B); the maximum rate of PER degradation, vd (C) and the Michaelis constant for PER degradation, Kd (D). We compared a model in which PER translation take place by an R-independent mechanism (first-order kinetics; ks = 1.48 h −1; Kr = 0 nM and Vr = 0 nM h −1; black curves) and a model in which PER translation take place by an R-dependent mechanism (Michaelis-Menten kinetics; ks = 0 h −1; Kr = 0.3 nM and Vr = 2.09 nM h −1; gray curves). Arrows indicate the values of the control parameters listed in S1 Table in S1 File.
Figs. 5 C and D (see also S11 and S12 Figs., B and C , in S1 File) show the relationships between delays and period for ks = 0 h −1 and nH = 4, which were qualitatively similar to those shown in S7 Fig. E in S1 File: the prevailing behavior observed was a monotonic relationship between delays and period, with slight deviations from this trend at each end of the δ t profile and in the region corresponding to very long τ of the δ n profile.
These results led us to ask how the delays arising from each translational mechanism considered here (i.e.: R-dependent vs R-independent) behave for a given (fixed) period of the molecular clock. In order to study this, we searched into the Kr-Vr parameter space shown in 5 Fig. (panels A and B) for a set producing oscillations with τ = 22.3 h, which is the period value reported for the original model [9]. For nH = 4 we found several combinations of the Vr and Kr parameter values that gave rise to oscillations with τ = 22.3 h, most of which yielded δn and δt values equal or longer than those obtained for the original model (S10 Fig. in S1 File). Indeed, for δt this result was independent of the τ fixed for comparison (5 Fig. C ; see also S11 Fig. B and C in S1 File). Notice that δt becomes longer as the PER translation becomes more saturated (compare the Kr isolines shown in 5 Fig. C with their I values shown in S3 Fig. A in S1 File).
Conversely, the δn versus τ profile exhibited two different behaviors: for oscillations with periods longer than 20 h the δn values obtained with an R-dependent translational mechanism were equal or longer than those obtained with an R-independent mechanism. On the other hand, for periods shorter than 20 h the R-dependent mechanism produced equal or shorter δ n’s than those obtained with an R-independent mechanism (5 Fig. D ; S12 Fig. B and C in S1 File). In contrast, for nH = 1 the relationship between delays and period was not monotonic (S8 Fig. C and D in S1 File see also S13 Fig. A and B in S1 File) and delays obtained from a model with an R-independent mechanism of translation (i.e.: Vr = 0 nM h −1) were equal or longer than those obtained with an R-dependent mechanism (i.e.: ks = 0 h −1), irrespectively of the τ fixed for comparison.
To further clarify the relationship between delays (δt and δn) and period (τ), we have normalized the delay values by the period length and characterized the normalized delay sensitivity regarding the Vr and Kr values (5 Fig. E and F ). For nH = 4 this analysis revealed changes in the delays that were independent of the period length, or, in other words, exclusively dependent on the parameters Vr and Kr. This effect seemed to be enhanced by the cooperative repression of per transcription (i.e.: nH = 4), because for nH = 1 the normalized delay values were more homogeneous than for nH = 4 (compare 5 Fig. E and F with S8 Fig. E and F in S1 File).
From these observations we can conclude that a translational regulation process which generates a PER translation rate of Michaelis-Menten type (R-dependent) will contribute with equal or longer delays (δt and δn) to the molecular clock than a mechanism in which the PER synthesis rate grows linearly with the per mRNA concentration (R-independent), as long as nH = 4 and the Kr-Vr parameter combination generates oscillations with periods longer than 20 h. We also observed that a saturated kinetics of PER translation enlarges the δ t values. These conclusions hold as long as the values for the rest of the parameters of our model are the same as those listed in S1 Table in S1 File.
Regarding the effect of the Hill coefficient (nH), we conclude that a non-cooperative transcriptional repression of per (nH = 1) tended to enlarge the delay values, irrespectively of the functional form of the translation kinetics considered here. For instance, for the original model (Kr = 0 nM, Vr = 0 nM h −1, ks = 2 h −1), a non-cooperative repression of per transcription resulted in longer delays (δn = 8.77 h and δt = 6.66 h) than those obtained with the cooperative model (nH = 4) (δn = 8.39 h and δt = 5.11 h) (S7 Fig. in S1 File, arrows) and the same qualitative result was obtained when the PER synthesis was achieved only by the R-dependent mechanism (S9 Fig. in S1 File). Furthermore, a non-cooperative transcriptional repression of per (nH = 1) tended to confine the diversity of delays observed within the Kr-Vr domain of self-sustained oscillations.
In addition, when we considered that PER translation was achieved by a combination of the two mechanisms proposed in our model (R-dependent plus R-independent), we observed that, by increasing ks, the delay distributions (both, the absolute and the normalized delays) became narrower than those observed for ks = 0 h −1 (S14 and S15 Figs. in S1 File). This result was independent of the nH value considered here (S16 and S17 Figs. in S1 File). As a final remark we note that the observed nontrivial phase shifts (delays) require of the coupling of the various components of the circadian clock. If, for instance, a sinusoidal per mRNA were used as an input signal, the introduction of a Michaelian term would not per se lead to a change of the delays. This can be seen by considering the uncoupled Eq. (2) and noticing that the maxima and minima of P0 coincide with the zeroes of the expression on the right-hand side, whose location is not changed by the presence of the Michaelian term.
Since assuming nH = 4 favored the periodic behavior of the system, facilitated the saturation of the R-dependent translational mechanism, increased the amplitude of mRNA oscillations and also increased the delays sensitivity to changes in the Vr and Kr values, we have continued our study considering that the repression of per transcription is a cooperative process.
Influence of other parameters on the period of oscillations
Previous studies have reported that the phosphorylations, protein stability and nuclear translocations are major period determinants in the molecular circadian clock [42, 44]. For instance, Goldbeter [6] has shown that the maximum rate of PER degradation is a key control parameter of the model that he proposed. On the basis of these antecedents, we studied the sensitivity of the oscillatory behavior of our model to changes in their parameter values. In particular, we were interested in determining whether or not the kinetics of PER translation modifies the sensitivity of the oscillatory behavior to changes in parameter values. We compared, therefore, the influence of the parameter variation on τ when the PER translation is assumed to occur by a single kinetic pathway, either with Michaelis-Menten kinetics (R-dependent mechanism; ks = 0 h −1) or with first-order kinetics (R-independent mechanism; Vr = 0 nM h −1 and Kr = 0 nM ). In order to conduct the comparison between these two conditions we established two similar systems, that is, systems exhibiting sustained oscillations with the same τ value, whose only difference was the kinetics of PER translation. Starting from our ‘master’ model, we looked for these two similar systems by exploring and specifying either the Kr-Vr subspace in one case, or the ks subspace in the other, while the rest of the parameter values were maintained as presented in S1 Table in S1 File. In constant darkness, the τ observed in the wild type (WT) Drosophila is close to 24 h (i.e.: τ = 23.8 h, [25]). Consequently, we decided to set the Kr and Vr values in one case, and the ks in the other case, in such a way that the τ value, in each system, was 23.8 h.
Therefore, we compared a model in which PER translation takes place by an R-independent mechanism (first-order kinetics; ks = 1.48 h −1; Kr = 0 nM and Vr = 0 nM h −1); and a model in which PER translation takes place by an R-dependent mechanism (Michaelis-Menten kinetics; ks = 0 h −1; Kr = 0.3 nM and Vr = 2.09 nM h −1, white dot within the Kr-Vr diagram shown in S3 Fig. A in S1 File, I ∼ 0.72). After establishing either the Kr and Vr or the ks values, we maintained them fixed. Then, we proceeded to determine how τ is altered when each parameter (other than ks, Vr, Kr and nH) is varied (one at a time) by ± 100% of their original value (S1 Table in S1 File). Results are shown in Fig. 6 and S18 Fig. in S1 File.
The black curves in Fig. 6 and S18 Fig. in S1 File correspond to the model in which the PER translation occurred by an R-independent mechanism, while the gray curves correspond to the model in which the PER translation occurred by an R-dependent mechanism. Arrows in 6 Fig. indicate the initial values of the control parameters (S1 Table in S1 File). For all the cases shown in Fig. 6 we observed that the τ profiles changed significantly as a consequence of the functional form of the translation kinetics. On the other hand, the cases shown in S18 Fig. in S1 File did not exhibit significant changes between the two conditions tested here.
Fig. 6 A shows the dependence of τon the Michaelis constant for per mRNA synthesis (v s). The model with an R-independent mechanism (black curve) exhibited a τ profile that initially decreased, v s value increased. On the other hand, in the model with Michaelis-Menten kinetics (gray curve), the τ length increased monotonically as vs increased. Leloup and Goldbeter [38] defined two different types of sensitivity, one related to the extent of τ variation derived from changes in the control parameter (i.e.: influence of each parameter on the period), and the other related to the size of the oscillatory domain (i.e.: higher sensitivity when the window for oscillations is relatively narrow). For simplicity, here we named these two sensitivities as type I and type II, respectively. On the basis of this information we observed that an R-dependent translation decreased the type I sensitivity (i.e.: the slope of the black curve was steeper than the slope of the gray curve), but slightly increased the type II sensitivity (notice that the vs range in which oscillations emerged was quite narrow when the model assumed an R-dependent translation).
Fig. 6 B shows the dependence of τ on the Michaelis constant for per mRNA degradation (Km). When PER translation was achieved by an R-independent mechanism (black curve), the τ initially decreased, then passed through a minimum and finally increased as the Km value increased. When PER translation was achieved by an R-dependent mechanism (gray curve), the τ profile monotonically decreased as Km increased. In this case, an R-dependent mechanism decreased the type I sensitivity (the absolute value of the gray-curve slope is smaller than the black curve slope) and increased the type II sensitivity (notice that the black curve continues to grow for Km > 0.45 nM).
Thus, for the vs and Km parameters, which are important to establish the steady levels of the per mRNA, the two types of sensitivity changed similarly. Interestingly, when vs and Km are control parameters and the PER translation follows an R-dependent mechanism, the decrease of the type I sensitivity can be interpreted as if the synthesis and degradation of per mRNA would have partially lost power to influence the oscillation period.
Fig. 6 C shows the dependence of τ on the maximum rate of PER degradation (vd). The τ profile derived from a model with an R-independent mechanism of PER translation (first-order kinetics; black curve), monotonically increased as vd increased. This was in agreement with the profile reported by Goldbeter [6]. The τ values also rose as vd increased for a model with an R-dependent mechanism (gray curve), but the range of vd values for which sustained oscillations emerged was smaller and the slope of the curve was steeper than those observed with an R-independent translational mechanism. Therefore, a Michaelis-Menten based mechanism of PER translation (R-dependent) increased both type I and type II sensitivities.
Fig. 6D shows the dependence of τ on the Michaelis constant for PER degradation (K d). The shape of the τ profiles did not change significantly between the two cases compared here: both profiles showed that τ monotonically decreased as Kd increased. Nevertheless, the τ profile derived from the model with an R-dependent translation (gray curve) exhibited a steeper slope than that obtained with the model where translation was achieved by an R-independent mechanism (black curve). In addition, the Kd range for which sustained oscillations emerged was shorter in the model with an R-dependent translation than in the model with an R-independent translation. Thus, in this case, an R-dependent mechanism increased the two types of sensitivity considered here. The results of Fig. 6 C and D revealed that an R-dependent translation increased the sensitivity of the oscillation period to changes in the PER degradation process.
Overall, these results suggest that an R-dependent translation leads to a change in the global sensitivity of the system, in which the synthesis and degradation of per mRNA becomes less decisive, but the PER degradation becomes more significant on the determination of the oscillation period. It is important to notice that these conclusions hold as long as the rest of the parameters (that is, those parameters not considered as control parameters for each sensitivity analysis) maintain the values listed in S1 Table in S1 File.
Testing our model with experimental results
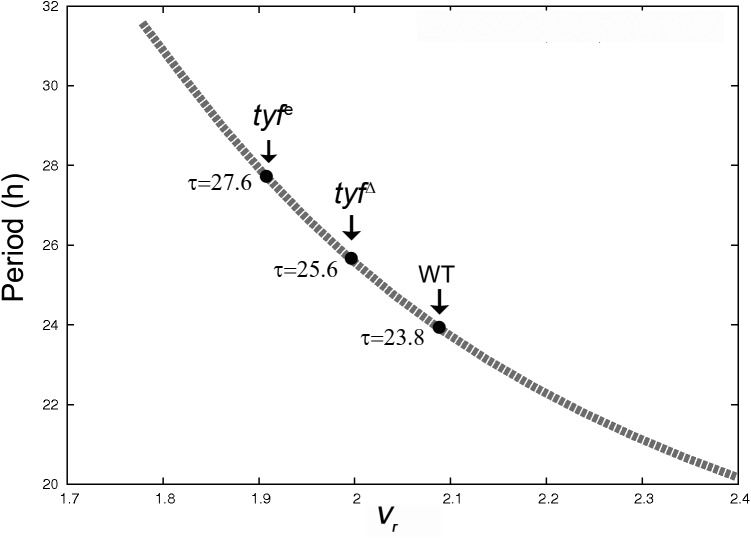
After the exhaustive characterization of our model introduced in the previous sections, we proceeded to validate it by comparing its results with experimental data. In flies, Lim and coworkers [25] reported a Drosophila strain which has mutated a gene named twenty four (tyf). This gene codifies for a protein (TYF) involved in the regulation of per mRNA translation. It seems that TYF forms a complex with PABP (a RNA-binding protein which binds to the poly(A) tail of mRNAs) and ATAXIN-2 (ATX2), which ultimately interacts with the per transcript and activates PER translation in pacemaker neurons to sustain robust rhythms [25, 47, 48]. These results highlight the role of TYF-PABP-ATX2 complexes for the proper PER translation in the Drosophila neural clockwork. Importantly, tyf mutants expressed oscillating PER levels in lateral clock neurons but the peak-to-trough amplitude was lower than in WT flies. Furthermore, the period of behavioral rhythms in tyf mutants is longer than in WT flies. Since the TYF-PABP-ATX2 complex can associate with per mRNA and enhance the PER translation, we posit that TYF-PABP-ATX2 effects on PER translation kinetics could be well represented by a translational process occurring with a Michaelis-Menten kinetics. To test this hypothesis, we used a version of our model that considers that PER translation is only achieved by an R-dependent mechanism (Michaelis-Menten kinetics; ks = 0 h −1). Here it is worth noting that, although in some conditions our model produces oscillations with τ = 22.3 h (Fig. 2 A and S1 A and S2 A Figs. in S1 File), this τ value does not correspond to the period observed in the WT Drosophila [25]. As shown in previous sections, we used this τ value only as a benchmark to conduct the characterization of our new version of the core clock model. Nevertheless, in order to see whether our simple model can account, at least qualitatively, for the experimental facts described above, it is important to show that it leads to circadian oscillations with τ = 23.8 h, which is the τ reported by Lim and coworkers for the (WT) Drosophila maintained in constant darkness [25].
Setting the translation-related parameters values at ks = 0 h −1, Kr = 0.3 nM and Vr = 2.09 nM h −1, (white dot within the Kr-Vr diagram shown in the S3 Fig. A in S1 File; I ∼ 0.72) and keeping the rest of the parameter values as listed in Table 1 in S1 File, our model exhibited sustained oscillations with τ = 23.8 h (Fig. 7 and Fig. 8 A ). The tyf hypomorphic mutants can be modeled as a system with smaller values of the Vr than WT flies because this parameter is related to the concentration of the TYF regulator (see discussion). Under these conditions, our model mimics the τ observed in the two tyf hypomorphic mutants reported by Lim and coworkers [25] (Fig. 7). Notice that τ became longer as the Vr parameter decreased, which is qualitatively similar to the experimental results stated above. Another qualitative similarity between the theoretical and the experimental results was the decrease in the peak-to-trough amplitude of PER levels (Fig. 8 A ) for the mutant flies. In addition, it is worth noting that our model predicted that the peak-to-trough amplitude a of the per mRNA for the mutants flies was lower than for WT flies, but the maximum levels of the per transcript were slightly higher (Fig. 8 A ). By comparing the temporal evolution of the per mRNA and total PER obtained with our model for the parameter values used in Fig. 7, we could roughly predict the time delays δt for WT and mutant flies (Fig. 8 B ). We observed that the δt (approximately 7.4 h) for the WT flies was shorter than those corresponding to the tyf Δ and the tyfe mutants (around 7.9 and 8.3 h, respectively, Fig. 8 B ). These general and qualitative observations regarding the delay could be tested in future experiments.
Figure 7. Comparison between theoretical and experimental results.
The dashed gray line shows the dependence of τ with the Vr parameter obtained with our model, for ks = 0 h −1, Kr = 0.3 nM h −1 and nH = 4. The periods of behavioral rhythms in wild type (WT) flies and tyf mutants (tyfe and tyf Δ) are also indicated with black points and arrows, according to [25]. See the text for further details
Figure 8. Circadian oscillations and delays in WT and tyf mutant flies.
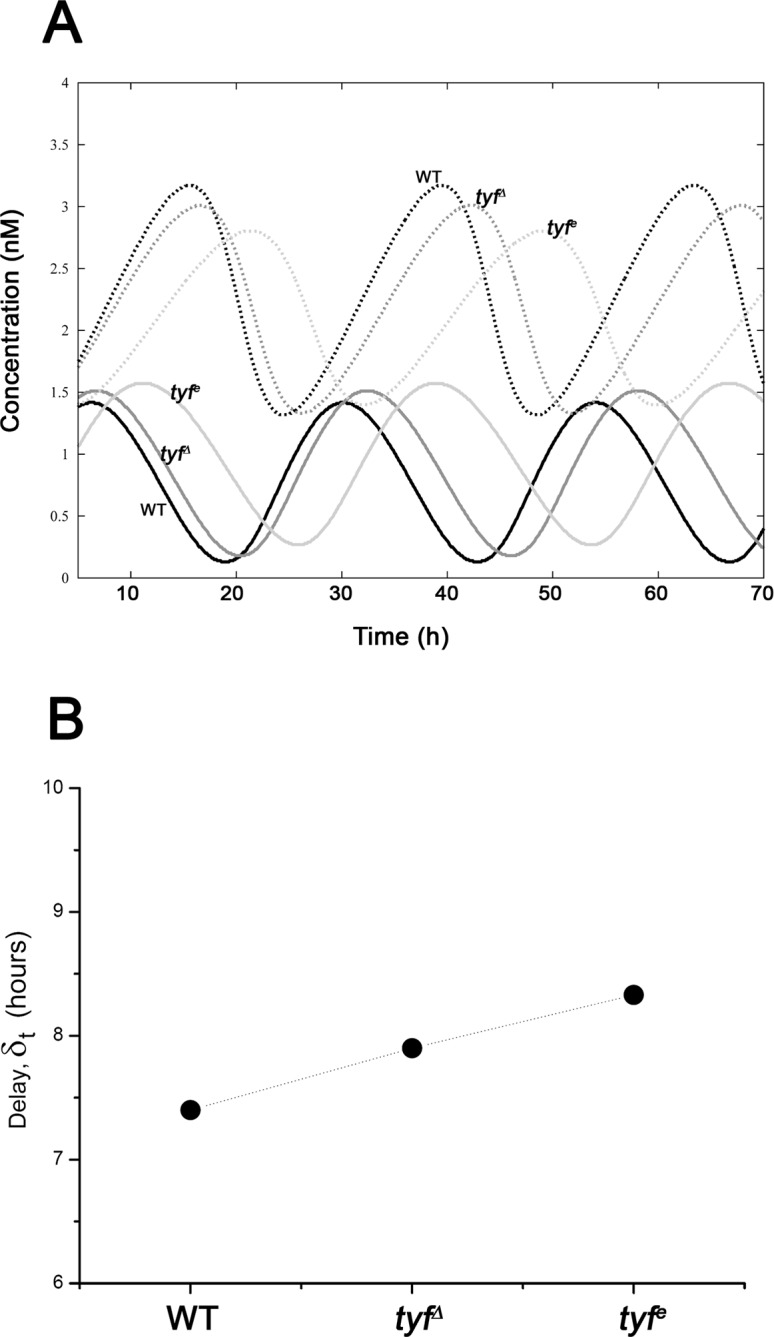
(A) Time evolution of the per transcript (solid lines) and total PER protein (dashed lines) in WT (black), tyf Δ (dark gray) and tyfe (light gray) flies. (B) Delay values (δt) of each fly strain. Results obtained with our model for ks = 0 h −1, Kr = 0.3 nM h −1 and nH = 4. Dotted line was plotted only for clarity purposes. See the text for further details.
Discussion
In this work we studied the dynamical behavior of a minimal circadian clock model in which, depending on the translation-related parameter values, the PER translation can be achieved either by a single translation mechanism (either with a first-order or a Michaelis-Menten kinetics) or through a double-translational mechanism (the sum of the first-order and Michaelis-Menten kinetics terms). This ‘master’ model enabled us to study and compare the effects of different translational kinetics on the dynamics of the molecular clock. Changes in the kinetics of PER translation may be one important consequence derived from the PER translational regulation. Although recent experimental findings have highlighted the role of translational regulation in the circadian dynamics [25, 26], this level of regulation was not considered in previous theoretical studies of the circadian clock.
PER translation by a single mechanism with Michaelis-Menten kinetics
Translational regulation is an important control point for shaping proteomes since it allows for more rapid changes in cellular protein concentrations than those achieved by transcriptional regulation [21, 49]. In mammalian cells, protein expression levels are primarily determined by regulation of translation and protein degradation [35]. In Drosophila, at least a 40% of the protein concentration is determined by these processes [50]. The kinetics of such biochemical processes are generally unknown and therefore, the choice of the kinetics laws and parameters to model these processes remains a challenge [44]. It is now recognized that the translation kinetics is a function of mRNA concentration as well as of other factors, such as the concentration of protein, tRNAs, ribosomes and translational regulators, among others. Similarly, protein degradation is also highly specific and tightly regulated. The involvement of multiple factors in the effective kinetics of both protein synthesis and degradation, suggests that these are nonlinear processes [34, 35]. In this regard, most of the previous models of the circadian clock assumed that the stationary concentration of total PER is mainly determined by its synthesis (considered as a first-order rate equation, dependent on the per mRNA levels) and degradation (modeled as a process that follows Michaelis-Menten kinetics) [6, 9, 29]. This description considers the nonlinearities related to the degradation process but not those related to translation. Although the assumption that the kinetics of PER synthesis follows a linear relationship with the amount of per mRNA has been satisfactory to model the molecular clock, we sought to determine how the clock dynamics is affected when nonlinearities in the translational process are included. Additionally, in recent years a growing number of reports have stressed the role of translational control mechanisms in the dynamics of circadian clocks [3, 20, 22, 23, 46]. In particular, several studies have pointed out that specific proteins act as enhancers of the Drosophila PER translation [25, 26, 47, 48]. According to these evidences, we considered that one simple way to take into account a nonlinear translational kinetics is by representing the PER translation as a process following a Michaelis-Menten kinetics. In addition to enhancing the global nonlinearity of the system without over-complicating the clock model, the saturable kinetics of Michaelis-Menten confers robustness to the biochemical oscillations by preventing the rates from increasing without limits [51]. Furthermore, a nonlinear saturable kinetics, such as the Michaelis-Menten, can roughly represent the kinetic consequence of a translational process regulated by one or multiple regulators acting either in a global and/or a specific fashion, which ultimately enhances the PER translation. Indeed, most models for the molecular clock have introduced nonlinearities (through a Michaelis-Menten kinetics) in other biochemical processes such as transcription, protein degradation and phosphorylation [43]. However the introduction of nonlinearities in the translational process has been rare. The only exception we know was the work of Kurosawa and Iwasa [52], which analytically proved (in circadian clock models with three or four variables) that the degree of saturation of enzyme kinetics affects the possibility of observing sustainable oscillations. They noticed that this effect varies systematically with the location of the reaction in the gene-protein network, and showed that large saturation indexes (I) for some reactions called in-loop (i.e.: PER translation, modification in the cytosol and transport to the nucleus) suppress the oscillation. Moreover, they also calculated the I values for each reaction step included in previous circadian clock models, and they showed that in those models the I values for in-loop reactions (like the PER translation) are small (between 0 and 0.5, see Fig. 5 within ref. [52]). We have numerically computed the saturation index for the PER translation reaction occurring through an R-dependent mechanism (see the Supporting Information and S3 Fig., A and E , in S1 File) and we also found that self-sustained oscillations emerged when the I values are small (between 0 and 0.5), which is consistent with the results of Kurosawa and Iwasa. Nevertheless, when nH = 4 our five-variable model showed that there is a small region within the Kr-Vr subspace in which self-sustained oscillations emerge even when the I values are larger than 0.5 (i.e.: I values between 0.5 and 0.8; S3 Fig. A in S1 File). This may suggest that in our five-variable model the saturation of PER translation does not necessarily imply an inhibition of the self-sustained oscillations.
Recently, the effect of Michaelis-Menten kinetics has been also discussed in the context of other cellular rhythms such as the activity of phosphofructokinase in glycolysis and cyclin-dependent kinases in the cell cycle [51], where it is shown and discussed how the Michaelis-Menten equation can be used to study the dynamical behavior of enzyme systems. Here we have shown that a PER translation process taking place exclusively via an R-dependent mechanism (Michaelis-Menten kinetics; ks = 0 h −1) was sufficient to obtain self-sustained oscillations within a specific Vr-Kr domain (Fig. 3 A ). Ultradian, circadian and infradian rhythms were observed, where the specific period, amplitude and delays depended on the specific values of the Vr and Kr parameters (Fig. 3 A , Fig. 6 and S4 Fig., A and B , in S1 File). These oscillatory properties also depended on the nH value (Fig. 4 A and S6, S8, S9 and S13 Figs. in S1 File) and other parameters of the model, therefore, the conclusions stated here hold as long as the values for the rest of the parameters of our model are the same as those listed in S1 Table in S1 File.
Extended clock models that incorporated the participation of tim and the formation of complexes between PER and TIM proteins revealed that the formation of the PER:TIM complexes favors sustained oscillations by introducing time delays in the negative feedback loop [7]. Qualitatively, this behavior is similar to that observed by a decrease of the Hill coefficient (nH) in core clock models, like the one presented here (S9 Fig. in S1 File). Recent work has highlighted the importance of studying how and to what extent the regulation of PER translation could contribute to those time delays observed experimentally [3]. Our study contributes to this point by showing that the specific kinetic function chosen to represent the translational kinetics would also affect significantly the time delays (Fig. 5 and S7–S17 Figs. in S1 File). Therefore, if the PER translational regulation involves a change in the translation kinetics, then it would also affect the time lags between the per transcript and protein expression profiles. Specifically, we showed that a PER translation taking place with a saturated Michaelis-Menten kinetics can contribute to the pace of the oscillator with longer delays than those produced by a first-order kinetics (Fig. 5), as long as nH = 4, the and the Kr-Vr parameter combination generates oscillations with periods longer than 20 h.
We remark that an increase in the delay follows a decrease in the Hill coefficient, independently of translation kinetics studied in this work (see S7 and S9 Figs. in S1 File). On the other hand, the presence of a Michaelian term in the translation could lead to an increase in the delays only if nH = 4, but not if nH = 1 (see Fig. 5 and S8 Fig. in S1 File). This suggest that the influence of the Hill coefficient on the delay goes beyond that of the translation kinetics. In addition, our results also indicate that the delay-shortening effect derived from an increase in the Hill coefficient can be compensated, at least in part, by changing the function describing the translation kinetics from first order to saturated Michaelis-Menten.
Previous studies showed that the dependence of τ on the PER degradation rate (vd) can adopt very different profiles depending on the kinetics of other processes, such as the per mRNA and protein degradation, PER phosphorylation-dephosphorylation and nuclear translocation [7, 53]. These results highlight the relevance of the nature of the kinetic functions describing the different biochemical processes on the clock properties. The results shown in Fig. 6 and S18 Fig. in S1 File revealed that the kinetic function describing the PER translational process also affected the dependence of τ on some of the non-translation related parameters of the model. Specifically, we observed that a saturable kinetics of PER translation changed the global sensitivity of the system, decreasing the sensitivity of the period to the synthesis and degradation of per mRNA, but increasing its sensitivity to PER degradation. Therefore, our results provide new information about how the kinetic laws of PER translation can modify the sensitivity of the oscillatory behavior of a core clock model to variations in their parameter values. These results have important implications if we assume that a regulatory process can act on the PER translation by changing its kinetic law. If that were the case, our results revealed that translational regulation may have strong implications for other biochemical process of the clock beyond translation itself. Another possibility would be to assume that the PER translational regulation proceeds without altering the kinetic laws but, instead, by changing the value of the translation-related parameters Vr and Kr. In this case, any alteration of the ‘normal’ regulation of PER translation must be reflected in such parameters. In this respect, the Drosophila TYF protein is a specific factor involved in the translational regulation of PER [25]. Hypomorphic mutations on the tyf gene result in a decreased expression of TYF, reducing the efficiency of PER translation. We have interpreted the effects of the tyf hypomorphic mutation as a decrease in the Vr parameter because such parameter is related to (but not solely determined by) the concentration of specific translational regulators, like TYF. By making this qualitative interpretation of our model, we observed that the period of tyf hypomorphic mutants is shorter than the one observed for WT flies (Fig. 7), which qualitatively agrees with the experimental observations [25]. A similar interpretation of our model can be applied to other recent studies, which reported new proteins involved in the PER translational regulation, such as NAT1 and ATAXIN-2 [26, 48]. Moreover, by interpreting that the tyf hypomorphic mutations will result in a decrease of the TYF levels and, therefore, in a decrease of the Vr parameter value of our model, we have made a qualitative prediction about the time delays expected for the flies carrying such mutations (Fig. 8).
PER translation by two independent mechanisms
Two main mechanisms of translation initiation have been described in Eukaryotes: the canonical cap-dependent and the apparently less frequent cap-independent mechanisms [54]. Transcripts can hypothetically use both mechanisms, but it is unclear to what extent each of these pathways contributes to the total protein expression. Indeed, it is likely that the relative efficiency of one translational mechanism as compared to the other depends on each specific mRNA and the cellular conditions being studied, among other factors [54, 55]. Additionally, recent experimental studies have suggested that PER in Drosophila and PER1 in mammals are translated not only by a cap-dependent mechanism but also by a cap-independent pathway [26, 36, 56]. Because some of the regulators involved in these two translation initiation mechanisms may be different, it is likely that they present different kinetic laws and, therefore, can be modeled as two independent pathways. In this work we studied whether a circadian clock model including a PER translation process consisting of two kinetically different pathways, led to self-sustained oscillations, and how the oscillatory properties of this system were modulated by the relative contribution of those mechanisms. It is worth to emphasize here that our work is the first to systematically study the dynamics of a circadian clock model with an overall translation process derived from two translational mechanisms with different kinetics. Our results showed that it is possible to obtain self-sustained oscillations, with a plethora of periodicities (including the circadian one) and amplitudes that depend on the specific values of the Kr, Vr and ks parameters. For nH = 4, the Vr-Kr domains, in which self-sustained oscillations exist, became larger as ks increased, which reflected an increase of the robustness of the system when the R-independent mechanism became more important. A similar behavior was observed when nH = 1, except for ks = 2, which exhibited a slight decrease in the self-sustained oscillatory domain. Nevertheless, the diversity of observed periods and delays decreased as ks grew, for both nH = 4 and nH = 1. In addition, for a fixed set of Vr and Kr parameter values, an increase in ks produced a shortening of the oscillation period, which was revealed by the progressive disappearance of infradian periods in the Kr-Vr diagrams as ks increased (compare the Kr-Vr diagrams for ks = 0.16 h −1 and ks = 2 h −1 in Figs. 3 A ).
It is well known that some drugs, like torin or rapamycin, cause inhibition of the canonical cap-dependent translation and shift translation toward a cap-independent activity [26, 28]. However, it is not clear yet whether and to what extent the cap-dependent and cap-independent initiation mechanisms of PER translation are relevant to the maintenance of the circadian period [26, 28]. In this context, mathematical models, like the one proposed here, may be useful to address these issues and to make reasonable predictions. For instance, it was shown that some translational regulators may be involved in the cap-independent translation of PER [28]. Therefore, it could be possible to draw a parallelism between the cap-independent/cap-dependent mechanisms and the R-dependent/R-independent mechanisms in our model, respectively.
This implies that the effect of torin or rapamycin on the cap-dependent translation may be represented in our model by abolishing or reducing the contribution of the R-independent mechanism to the overall translation, achieved by decreasing the value of the ks parameter. Under these conditions, at least one possible prediction emerging from our work is that treatment with those inhibitors will lengthen the period of the molecular clock (compare the Kr-Vr diagrams for ks = 0.16 h −1 and ks = 2 h −1 in Fig. 3 A ) and it is expected to be experimentally tested in future works.
Future directions and Concluding Remarks
More refined models of protein production could be also assumed in the future. For instance, an interesting approach could be to consider an oscillatory (circadian) regulation of PER translation, since recent studies in mammals revealed that translation is regulated by the circadian clock both globally (by translation initiation factors) and specifically (by RNA-Binding Proteins, micro RNAs and/or poly(A) tail length regulation) [20, 22, 27, 28].
It is worth noting that deterministic models of the circadian clock (as the one presented here) have been useful for the study of diverse aspects of circadian rhythmicity as long as the number of molecules involved in the oscillatory mechanism exceeds a few tens or hundreds of molecules. However, in some cellular conditions the number of molecules involved in the oscillatory mechanism may be small and deterministic models may reach their limits. In this situation the effect of the intrinsic molecular noise becomes important and it becomes necessary to resort to stochastic models. Previous stochastic models show that circadian oscillations are robust even at low numbers of molecules, although there is a threshold below which the noise obliterates the circadian rhythmicity [9, 57]. In addition, a variety of factors (such as the degree of cooperativity of repression, distance from the bifurcation point, the magnitude of the rate constants characterizing binding of the repressor to the gene, etc.) affects the robustness of the circadian oscillations in the presence of molecular noise. Thus, it would be interesting to explore the implications of assuming a nonlinear saturable kinetics for PER translation in stochastic models of the circadian clock, a problem that will be addressed in future works.
Our results have significant biological relevance because they characterized, for the first time, how different PER translational kinetics affects the generation and maintenance of circadian rhythms at molecular level. We showed that it is possible to modify significantly the period, amplitude, and delays of the self-sustained oscillations by changing the functional form of the PER translation kinetics, by changing the translation-related parameter values, or by considering the PER translation derived from two kinetically different pathways. We have interpreted the effective translational kinetics as the result of the regulation of PER synthesis, which might modify the translational functional term(s) and/or its kinetic parameters. Besides, our model provides results that are in qualitative agreement with experimental findings related to the PER translational regulation of the Drosophila molecular clock and supplies helpful information for interpreting and reassessing the significance of translational regulation in the molecular circadian clock.
Supporting Information
(DOC)
Acknowledgments
The authors thank CONICET (Argentina) for support.
Data Availability
All relevant data are within the paper and its Supporting Information files.
Funding Statement
The authors have no support or funding to report.
References
- 1. Mohawk JA, Takahashi JS (2011) Cell autonomy and synchrony of suprachiasmatic nucleus circadian oscillators. Trends in Neurosciences 34: 349–358. 10.1016/j.tins.2011.05.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Lowrey P, Takahashi J (2011) Chapter 6—genetics of circadian rhythms in mammalian model organisms. In: Brody S, editor, The Genetics of Circadian Rhythms, Academic Press, volume 74 of Advances in Genetics pp. 175–230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Hardin P (2011) Chapter 5—molecular genetic analysis of circadian timekeeping in drosophila. In: Brody S, editor, The Genetics of Circadian Rhythms, Academic Press, volume 74 of Advances in Genetics pp. 141–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Ukai H, Ueda HR (2010) Systems biology of mammalian circadian clocks. Annual Review of Physiology 72: 579–603. 10.1146/annurev-physiol-073109-130051 [DOI] [PubMed] [Google Scholar]
- 5. Mirsky H, Liu A, Welsh D, Kay S, Doyle F (2009) A model of the cell-autonomous mammalian circadian clock. Proceedings of the National Academy of Sciences 106: 11107–11112. 10.1073/pnas.0904837106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Goldbeter A (1995) A model for circadian oscillations in the drosophila period protein (per). Proceedings of the Royal Society of London Series B: Biological Sciences 261: 319–324. 10.1098/rspb.1995.0153 [DOI] [PubMed] [Google Scholar]
- 7. Leloup J, Goldbeter A (1998) A model for circadian rhythms in drosophila incorporating the formation of a complex between the per and tim proteins. Journal of Biological Rhythms 13: 70–87. 10.1177/074873098128999934 [DOI] [PubMed] [Google Scholar]
- 8. Gonze D, Leloup J, Goldbeter A (2000) Theoretical models for circadian rhythms in neurospora and drosophila. Comptes Rendus de l’Académie des Sciences—Series III—Sciences de la Vie 323: 57–67. 10.1016/S0764-4469(00)00111-6 [DOI] [PubMed] [Google Scholar]
- 9. Gonze D, Halloy J, Goldbeter A (2002) Robustness of circadian rhythms with respect to molecular noise. Proceedings of the National Academy of Sciences 99: 673–678. 10.1073/pnas.022628299 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Leloup J, Goldbeter A (2003) Toward a detailed computational model for the mammalian circadian clock. Proceedings of the National Academy of Sciences 100: 7051–7056. 10.1073/pnas.1132112100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Forger D, Peskin C (2003) A detailed predictive model of the mammalian circadian clock. Proceedings of the National Academy of Sciences 100: 14806–14811. 10.1073/pnas.2036281100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Lema M, Golombek D, Echave J (2000) Delay model of the circadian pacemaker. Journal of Theoretical Biology 204: 565–573. 10.1006/jtbi.2000.2038 [DOI] [PubMed] [Google Scholar]
- 13. Axmann I, Legewie S, Herzel H (2007) A minimal circadian clock model. Genome Informatics 18: 54–64. 10.1142/9781860949920_0006 [DOI] [PubMed] [Google Scholar]
- 14. Risau-Gusman S, Gleiser P (2012) Modelling the effect of phosphorylation on the circadian clock of drosophila. Journal of Theoretical Biology 307: 53–61. 10.1016/j.jtbi.2012.05.003 [DOI] [PubMed] [Google Scholar]
- 15. Forger DB, Peskin CS (2005) Stochastic simulation of the mammalian circadian clock. Proceedings of the National Academy of Sciences 102: 321–324. 10.1073/pnas.0408465102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Gonze D, Goldbeter A (2006) Circadian rhythms and molecular noise. Chaos: An Interdisciplinary Journal of Nonlinear Science 16: 026110–026121. 10.1063/1.2211767 [DOI] [PubMed] [Google Scholar]
- 17. Garbarino-Pico E, Green CB (2007) Posttranscriptional regulation of mammalian circadian clock output. Cold Spring Harbor Symposia on Quantitative Biology 72: 145–156. 10.1101/sqb.2007.72.022 [DOI] [PubMed] [Google Scholar]
- 18. Garbarino-Pico E, Nieto P, Guido M (2011) Circadian posttranscriptional regulation: Not only transcription and protein modifications are required for accurate biological clockwork. In: Golovkin L, Maliszkewicz A, editors, Circadian Rhythms: Biology, Cognition and Disorders, Nova Science Publishers, Inc., Human Anatomy and Physiology; pp. 247–276. [Google Scholar]
- 19. Keene JD (2007) Biological clocks and the coordination theory of rna operons and regulons. Cold Spring Harbor Symposia on Quantitative Biology 72: 157–165. 10.1101/sqb.2007.72.013 [DOI] [PubMed] [Google Scholar]
- 20. Kojima S, Sher-Chen E, Green C (2012) Circadian control of mrna polyadenylation dynamics regulates rhythmic protein expression. Genes and Development 26: 2724–2736. 10.1101/gad.208306.112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Gebauer F, Hentze M (2004) Molecular mechanisms of translational control. Nature Reviews Molecular Cell Biology 5: 827–835. 10.1038/nrm1488 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Jouffe C, Cretenet G, Symul L, Martin E, Atger F, et al. (2013) The circadian clock coordinates ribosome biogenesis. PLoS Biology 11: e1001455 10.1371/journal.pbio.1001455 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Reddy A, Karp N, Maywood E, Sage E, Deery M, et al. (2006) Circadian orchestration of the hepatic proteome. Current Biology 16: 1107–1115. 10.1016/j.cub.2006.04.026 [DOI] [PubMed] [Google Scholar]
- 24. Kojima S, Shingle D, Green CB (2011) Post-transcriptional control of circadian rhythms. Journal of Cell Science 124: 311–320. 10.1242/jcs.065771 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Lim C, Lee J, Choi C, Kilman V, Kim J, et al. (2011) The novel gene twenty-four defines a critical translational step in the drosophila clock. Nature 470: 399–403. 10.1038/nature09728 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Bradley S, Narayanan S, Rosbash M (2012) Nat1/dap5/p97 and atypical translational control in the drosophila circadian oscillator. Genetics 192: 943–957. 10.1534/genetics.112.143248 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Kojima S, Matsumoto K, Hirose M, Shimada M, Nagano M, et al. (2007) Lark activates post-transcriptional expression of an essential mammalian clock protein, period1. Proceedings of the National Academy of Sciences 104: 1859–1864. 10.1073/pnas.0607567104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Lee K, Woo K, Kim D, Kim T, Shin J, et al. (2012) Rhythmic interaction between period1 mrna and hnrnp-q leads to circadian time-dependent translation. Molecular and Cellular Biology 32: 717–728. 10.1128/MCB.06177-11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Nandi A, Vaz C, Bhattacharya A, Ramaswamy R (2009) mirna-regulated dynamics in circadian oscillator models. BMC Systems Biology 3: 45–61. 10.1186/1752-0509-3-45 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Dunlap J, Loros J, DeCoursey P (2004) Chronobiology: Biological Timekeeping. Sinauer Associates.
- 31. Beersma DG (2005) Why and how do we model circadian rhythms? Journal of Biological Rhythms 20: 304–313. 10.1177/0748730405277388 [DOI] [PubMed] [Google Scholar]
- 32. Roenneberg T, Chua EJ, Bernardo R, Mendoza E (2008) Modelling biological rhythms. Current Biology 18: R826–R835. 10.1016/j.cub.2008.07.017 [DOI] [PubMed] [Google Scholar]
- 33. Dibner C, Sage D, Unser M, Bauer C, d’Eysmond T, et al. (2008) Circadian gene expression is resilient to large fluctuations in overall transcription rates. The EMBO Journal 28: 123–134. 10.1038/emboj.2008.262 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. de Sousa Abreu R, Penalva L, Marcotte E, Vogel C (2009) Global signatures of protein and mrna expression levels. Molecular BioSystems 5: 1512–1526. 10.1039/b908315d [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Vogel C, Marcotte E (2012) Insights into the regulation of protein abundance from proteomic and transcriptomic analyses. Nature Reviews Genetics 13: 227–232. 10.1038/nrg3185 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Lee K, Kim S, Kim D, Kim S, Kim K (2012) Internal ribosomal entry site-mediated translation is important for rhythmic period1 expression. PLoS ONE 7: e37936 10.1371/journal.pone.0037936 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Brown S, Kowalska E, Dallmann R (2012) (re)inventing the circadian feedback loop. Developmental Cell 22: 477–487. 10.1016/j.devcel.2012.02.007 [DOI] [PubMed] [Google Scholar]
- 38. Leloup JC, Goldbeter A (2004) Modeling the mammalian circadian clock: Sensitivity analysis and multiplicity of oscillatory mechanisms. Journal of Theoretical Biology 230: 541–562. 10.1016/j.jtbi.2004.04.040 [DOI] [PubMed] [Google Scholar]
- 39. Hafner M, Koeppl H, Gonze D (2012) Effect of network architecture on synchronization and entrainment properties of the circadian oscillations in the suprachiasmatic nucleus. PLoS Comput Biol 8: e1002419 10.1371/journal.pcbi.1002419 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. So W, Rosbash M (1997) Post-transcriptional regulation contributes to drosophila clock gene mrna cycling. EMBO J 16–23: 7146–7155. 10.1093/emboj/16.23.7146 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Stanewsky R, Lynch K, Brandes C, Hall J (2002) Mapping of elements involved in regulating normal temporal period and timeless rna expression patterns in drosophila melanogaster. Journal of Biological Rhythms 17: 293–306. 10.1177/074873002129002609 [DOI] [PubMed] [Google Scholar]
- 42. Korencic A, Bordyugov G, Kosir R, Rozman D, Golicnik M, et al. (2012) The interplay of cis-regulatory elements rules circadian rhythms in mouse liver. PLoS One 7: e46835 10.1371/journal.pone.0046835 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Relógio A, Westermark P, Wallach T, Schellenberg K, Kramer A, et al. (2011) Tuning the mammalian circadian clock: Robust synergy of two loops. PLoS Compututational Biology 7: e1002309 10.1371/journal.pcbi.1002309 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Bordyugov G, Westermark P, Korencic A, Bernard S, Herzel H (2013) Mathematical modeling in chronobiology. In: Kramer A, Merrow M, editors, Circadian Clocks, Springer Berlin Heidelberg, volume 217 of Handbook of Experimental Pharmacology pp. 335–357. [DOI] [PubMed] [Google Scholar]
- 45. Dunlap JC (2006) Running a clock requires quality time together. Science 311: 184–186. 10.1126/science.1122839 [DOI] [PubMed] [Google Scholar]
- 46. Harms E, Kivimae S, Young M, Saez L (2004) Posttranscriptional and posttranslational regulation of clock genes. Journal of Biological Rhythms 19: 361–373. 10.1177/0748730404268111 [DOI] [PubMed] [Google Scholar]
- 47. Lim C, Allada R (2013) Ataxin-2 activates period translation to sustain circadian rhythms in drosophila. Science 340: 875–879. 10.1126/science.1234785 [DOI] [PubMed] [Google Scholar]
- 48. Zhang Y, Ling J, Yuan C, Dubruille R, Emery P (2013) A role for drosophila atx2 in activation of per translation and circadian behavior. Science 340: 879–882. 10.1126/science.1234746 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Gebauer F, Preiss T, Hentze M (2012) From cis-regulatory elements to complex rnps and back. Cold Spring Harbor Perspectives in Biology 4: 14 10.1101/cshperspect.a012245 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Laurent J, Vogel C, Kwon T, Craig S, Boutz J, et al. (2010) Protein abundances are more conserved than mrna abundances across diverse taxa. Proteomics 10: 4209–4212. 10.1002/pmic.201000327 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Goldbeter A (2013) Oscillatory enzyme reactions and michaelis menten kinetics. FEBS Letters 587: 2778–2784. 10.1016/j.febslet.2013.07.031 [DOI] [PubMed] [Google Scholar]
- 52. Kurosawa G, Iwasa Y (2002) Saturation of enzyme kinetics in circadian clock models. Journal of Biological Rhythms 17: 568–577. 10.1177/0748730402238239 [DOI] [PubMed] [Google Scholar]
- 53. Gerard C, Gonze D, Goldbeter A (2009) Dependence of the period on the rate of protein degradation in minimal models for circadian oscillations. Phil Trans R Soc 367: 4665–4683. 10.1098/rsta.2009.0133 [DOI] [PubMed] [Google Scholar]
- 54. Thompson S (2012) So you want to know if your message has an ires? Wiley Interdisciplinary Reviews: RNA 3: 697–705. 10.1002/wrna.1129 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Sonenberg N, Hinnebusch G (2009) Regulation of translation initiation in eukaryotes: Mechanisms and biological targets. Cell 136: 731–745. 10.1016/j.cell.2009.01.042 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Kim D, Woo K, Lee K, Kim T, Kim KT (2010) hnrnp q and ptb modulate the circadian oscillation of mouse rev-erb via ires-mediated translation. Nucleic Acids Research 38: 7068–7078. 10.1093/nar/gkq569 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Gonze D, Halloy J, Goldbeter A (2002) Deterministic versus stochastic models for circadian rhythms. Journal of Biological Physics 28: 637–653. 10.1023/A:1021286607354 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(DOC)
Data Availability Statement
All relevant data are within the paper and its Supporting Information files.