Figure 1.
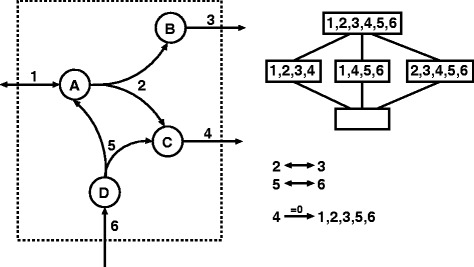
Example network with corresponding lattice and coupling relations. The network contains the set of metabolites and the set of reactions . We assume that all coefficients s mr of the stoichiometric matrix S belong to {0,+1,−1}. Thus, reaction 2 has the stoichiometry s A2=−1,s B2=s C2=1 and s D2=0. The set of irreversible reactions is . A possible flux vector satisfying the steady-state condition S v=0 is v=(0,1,1,2,1,1) with supp v={2,3,4,5,6}. The corresponding lattice contains the trivial element ∅ representing the vector v=0 and the minimal (non-trivial) elements {1,2,3,4},{1,4,5,6} and {2,3,4,5,6}. The maximal element is {1,2,3,4,5,6}, i.e., there is no blocked reaction. a) There are two pairs of partially coupled reactions, namely 2⇔3 and 5⇔6. Therefore, no knockout sets containing reaction 3 or 5 need to be analysed. The impact of a double knockout of {3,r} will be the same as for {2,r}. b) Reaction 1 is coupled to reaction 4. Thus, a double knockout of {1,4} will have the same effect as the simple knockout of 4. In both cases, all reactions {1,2,3,4,5,6} get blocked.
