Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2015 Jan 22;9:2. doi: 10.3389/fnins.2015.00002

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

Copyright © 2015 Vogginger, Schüffny, Lansner, Cederström, Partzsch and Höppner.

This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

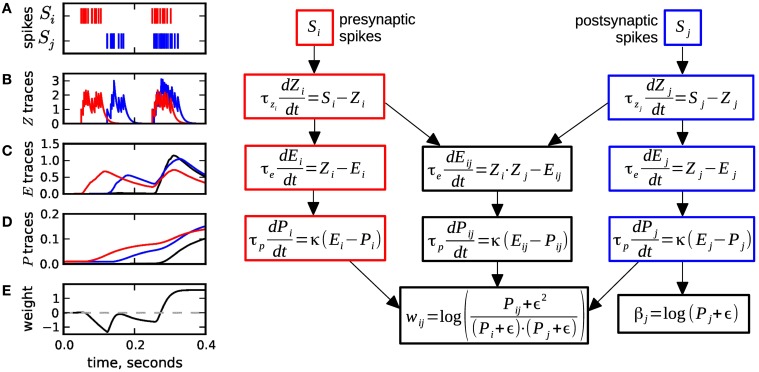
PMC Copyright notice

Equations and sample traces of the spike-based BCPNN learning rule. (A) Presynaptic (red) S_i and postsynaptic (blue) S_j spike trains serve as input to a BCPNN synapse. (B) The input spike trains are low pass filtered into the Z traces with time constants τ_{z_i},τ_{z_j}. (C) E traces compute the low-pass filter of Z traces with τ_e. The E_ij variable (black) tracks coincident pre- and postsynaptic activity. (D) E traces are passed on to the P traces and low-pass filtered with τ_p. (E) The P traces are used to compute the postsynaptic bias β_j and the synaptic weight w_ij, which can vary between positive and negative values. Usually, the dynamics get slower from B to D: τ_{z_i}, τ_{z_j} ≤ τ_e ≤ τ_p. Figure redrawn from Tully et al. (2014).