Evolution Alters the Enzymatic Reaction Coordinate of Dihydrofolate Reductase

Abstract

How evolution has affected enzyme function is a topic of great interest in the field of biophysical chemistry. Evolutionary changes from Escherichia coli dihydrofolate reductase (ecDHFR) to human dihydrofolate reductase (hsDHFR) have resulted in increased catalytic efficiency and an altered dynamic landscape in the human enzyme. Here, we show that a subpicosecond protein motion is dynamically coupled to hydride transfer catalyzed by hsDHFR but not ecDHFR. This motion propagates through residues that correspond to mutational events along the evolutionary path from ecDHFR to hsDHFR. We observe an increase in the variability of the transition states, reactive conformations, and times of barrier crossing in the human system. In the hsDHFR active site, we detect structural changes that have enabled the coupling of fast protein dynamics to the reaction coordinate. These results indicate a shift in the DHFR family to a form of catalysis that incorporates rapid protein dynamics and a concomitant shift to a more flexible path through reactive phase space.

Introduction

Enzymatic catalysis, defined as the degree to which an enzyme is able to accelerate the rate of a given chemical reaction,¹ remains to be fully understood. Enzymes are able to achieve rate enhancements in the range of 10¹⁵–10¹⁷ in comparison to uncatalyzed reactions,² exceeding those of any artificial catalysts by many orders of magnitude.³ Since the theory of transition state stabilization was introduced by Linus Pauling,⁴ enzymatic catalysis has been historically defined in terms of the ability of an enzyme to accommodate the electrostatic and geometric configuration of a chemical transition state.⁵ According to this theory, the rate enhancement of an enzyme-catalyzed reaction is proportional to the free energy difference between the enzymatic and unbound transition state,⁶ which is of course a truism. The real question is what is the physical origin of that free energy difference.

Over the course of an enzymatic cycle, the protein bulk of an enzyme can sample a myriad of conformations⁷ resulting in a complex hierarchy of dynamic transitions over a wide range of time scales.^8,9 One of the most widely studied enzymes with regard to the impact of protein dynamics on catalysis occurring on a time scale of microseconds to milliseconds is dihydrofolate reductase (DHFR).^10,11 This enzyme is essential for maintenance of the proper intracellular concentration of tetrahydrofolate, a coenzyme involved in the biosynthesis of purines, pyrimidines, and some amino acids.¹² DHFR catalyzes the reduction of dihydrofolate to tetrahydrofolate via a protonation step and a hydride transfer. Protonation of the N5 atom of dihydrofolate occurs by way of solvent exchange, whereas hydride transfer from the nicotinamide ring of the cofactor nicotinamide adenine dinucleotide phosphate (NADPH) to the C6 position of the substrate is directly catalyzed by the enzyme.²

In Escherichia coli DHFR (ecDHFR), the hydride transfer step is mediated by thermally averaged equilibrium fluctuations of the enzyme^8,13 that result in a small population of reactive conformations.^14,15 Several evolutionarily conserved residues distal from the active site of ecDHFR have been implicated as key loci in the motions allowing for hydride transfer.⁸ Mutation of these residues leads to a decrease in the catalytic rate by altering the probabilistic sampling of distinct enzymatic conformations.¹⁶ These ecDHFR motions are slow compared to the time scale of chemical transformation (femtoseconds), and thus can only impact the catalyzed reaction in a statistical manner.¹⁷ In contrast, it is possible that protein dynamics occurring on the femtosecond time scale, which is the same time scale as chemical bond vibrations, can dynamically couple to enzymatic barrier crossing.^1,3,18 In this manuscript, we will show that this is obtained in human DHFR (hsDHFR).

These fast protein motions, termed promoting vibrations (PVs), are types of nonequilibrium density fluctuations that propagate through specific structures within a protein.¹⁹ These motions act to dynamically modulate both the width and height of the chemical barrier, resulting in an increase in reaction rate.^1,3 Although PVs have been identified in the reaction coordinates of several enzymes,²⁰⁻²³ fast enzyme dynamics have been shown to have no effect on hydride transfer catalyzed by ecDHFR.²⁴ Furthermore, the network of coupled protein dynamics of ecDHFR is incapable of sustaining dynamic correlations between fast vibrational motions at distances greater than 4–6 Å.¹⁷ This characteristic of the dynamic landscape of ecDHFR obviates the possibility of the incorporation of fast motions of the protein bulk in the ecDHFR reaction coordinate,¹⁷ and previous work in our group confirms the absence of a PV in this enzyme.²⁵

Recently, interest has developed regarding the question of how evolution has altered the catalytic and dynamic properties of DHFR. A study of hsDHFR conducted by Wright and co-workers revealed that the human enzyme exhibits a dynamic landscape that is highly divergent from that of ecDHFR.²⁶ This effect was primarily observed in the dynamics of specific mobile loops of the enzyme, which exhibit smaller scale fluctuations in hsDHFR compared to those in ecDHFR, which is due to increased flexibility resulting from the incorporation of additional residues. Accompanying this change in dynamic landscape in the human enzyme is tighter active site packing. In hsDHFR, ligand flux is mediated by a twisting-hinge motion of the Met20 domain, whereas the opening and closing of the Met20 loop modulates ligand binding and unbinding in ecDHFR. The human enzyme also lacks conformational changes that differentiate the Michaelis complex and the product ternary complex in prokaryotic forms of DHFR, including ecDHFR. Because hsDHFR is approximately 10 times more susceptible to end-product inhibition, the authors conclude that the evolution of a new dynamic mechanism in hsDHFR might be an adaptation in response to the disparate relative concentrations of NADPH in relation to NADP⁺ that is observed in vertebrate versus prokaryotic cells (100:1 ratio in humans and 1:1 in E. coli).²⁶

Another relevant study conducted by Liu et al. showed that specific mutations along the evolutionary path from esDHFR to hsDHFR, also known as phylogenetically coherent events (PCEs), affect the binding properties and catalytic efficiency of the enzyme.²⁷ The locations of the PCEs discussed in this paper are shown in Figure 1 for the hsDHFR system along with a sequence alignment comparing the human and E. coli enzymes. The most recent of these PCEs, a PWPP modification of the Met20 region (21-PWNLPADL-27 in ecDHFR and 24-PWPPLRNE-31 in hsDHFR), prevents this loop from assuming an open conformation in the human enzyme and negatively impacts the catalytic rate when expressed individually in an E. coli chimera enzyme. Mutating two additional PCE regions (ecDHFR G51 to hsDHFR 62-PEKN-65 and a single L28F mutation) to humanlike sequences in an E. coli variant rectified the PWPP catalytic deficit,²⁷ and the end result is a measurable improvement in catalytic efficiency in hsDHFR compared to that of ecDHFR.

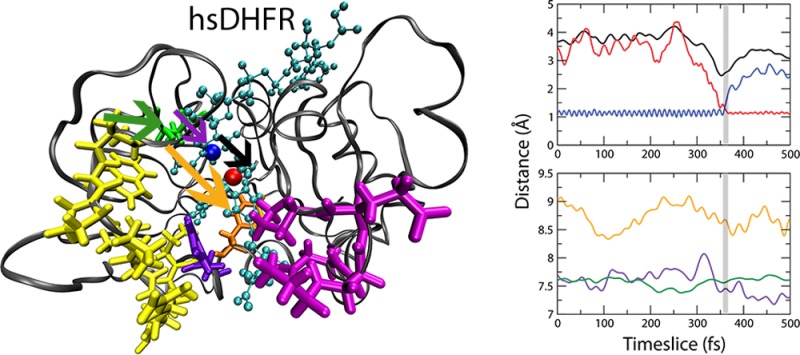
Figure 1.

Michaelis complex of hsDHFR showing the locations of the putative PV residues and a sequence alignment for the human and E. coli enzymes. The hsDHFR sequence is shown in bold. In the hsDHFR image, the bound ligands are cyan, the hydride donor is blue, and the hydride acceptor is red. PV residues are depicted as follows: I17 = green, F35 = orange, 24-PWPPLRNE-31 of the Met20 loop = yellow, F32 = violet, and 62-PEKN-65 = magenta. The backbone of the rest of the protein is gray. Regarding PCEs, the PWPP modification overlaps with the yellow residues; 24-PWPPLRNE-31, 62-PEKN-65 (magenta), and L28F (violet) mutational events are shown explicitly.

Considering the altered dynamic landscape of hsDHFR in combination with the effects of specific mutational events on DHFR catalysis, our group hypothesized that fast protein dynamics might be dynamically coupled to hsDHFR-catalyzed hydride transfer. In this work, we present the results of a transition path sampling (TPS)²⁸ study indicating the presence of a PV in the reaction coordinate of hsDHFR. The advantage of TPS is that it is completely unbiased, unlike other sampling methodologies such as umbrella sampling. It is also entirely rigorous, with the only approximations being the use of quantum mechanical/molecular mechanical (QM/MM) simulations and semiempirical treatment of the quantum region. We stress that the trajectories found via TPS are classical in nature; in other words, they do not include the effects of hydride tunneling or zero point energy. We feel that such inclusion would not effect our conclusions for two reasons. First, the promoting vibration, by compressing the donor and acceptor, causes the barrier to be both lower and thinner. Tunneling would only favor this effect. Second, for other hydride transfer enzymes, and alcohol dehydrogenase in particular, there is some indication that tunneling plays a small role.²⁹

To carry out the specific analyses discussed throughout this paper, we first generated a transition path ensemble (TPE) for the hsDHFR hydride transfer reaction consisting of 200 individual reactive trajectories. We produced these trajectories via a microcanonical TPS algorithm adapted for the study of enzymatic reactions²¹ that maintains an acceptance ratio of ∼25%. To obtain a transition state ensemble (TSE), or a set of atomic coordinates along the stochastic separatrix,³⁰ we calculated the commitment probability of every 10th trajectory in the hsDHFR TPE. We considered the time of barrier crossing to correspond to the time necessary for the committor to rise from 0.1 to 0.9, and we regarded the transition state of each trajectory to be the time slice with a committor value closest to 0.5. For comparison purposes, we also utilized an ecDHFR TPE and TSE calculated previously.²⁵

Methods

Simulation Details

We performed all steps for system setup using the program CHARMM^31,32 unless otherwise noted. To obtain initial atomic coordinates, we utilized the crystal structure of human DHFR in a ternary complex with the cofactors NADPH and folic acid, which is a substrate mimic. This structure was solved to a resolution of 1.20 Å by Wright et al. (PDB code 4M6K).²⁶ To create a reactive complex to study hydride transfer using the coordinates of folic acid, we changed the protonation states of N1, N8, and protonated C6 and generated atomistic parameters for this new ligand using the program DiscoveryStudio25. Also using this program, we added C-terminal residues Met1–Gly3, which were not resolved in the original crystal structure. We employed protonation states of all acidic and basic amino acids corresponding to said state at physiological pH as determined by CHARMM. To ready the complex for QM/MM simulation, we isolated the quantum mechanical region (the dihydronicotinamide and ribose group of NADPH and the majority of dihydrofolate, excluding the glutamate tail) as a separate residue, patched the boundary atoms to the classical regions using the command PRES, and constructed a distinct parameter file for this new residue. For this new residue, we used a nonstandard potential first calculated by Garcia-Viloca et al.¹² Following this step, we solvated the entire complex with an 85 Å-diameter sphere of TIP3 water models,³³ incorporated all crystallographic waters as TIP3 models, and neutralized the charge of the system with four potassium ions.

We conducted all molecular dynamics (MD) and QM/MM simulations presented in this work using version 35 of the program CHARMM.^31,32 For classical simulations, we implemented the CHARMM27 all-atom force field. During QM/MM, we simulated the quantum region using the AM1 potential³⁴ and treated the boundary atoms using the generalized hybrid orbital (GHO) method.³⁵ We conducted all integrations of forces for MD or QM/MM using time steps of 1 fs. The protocol we utilized to minimize, heat, and equilibrate the hsDHFR system was selected to mimic that implemented in our previous study on ecDHFR.²⁵ For minimization, we first constrained all atoms except TIP3P waters and potassium ions using a harmonic potential of 100 kcal mol^–1 Å^–1 and performed 100 steps of steepest descent (SD) followed by 100 steps of the adopted basis Newton–Raphson method (ABNR). Next, we constrained only the protein and ligand atoms with 100 kcal mol^–1 Å^–1 of harmonic force and conducted 100 steps of ABNR. Next, we performed iterative minimization cycles with the protein and ligand atoms constrained using force constants of 75, 50, and 25 kcal mol^–1 Å^–1, successively. Then, we conducted an unconstrained minimization using QM/MM for 100 steps of ABNR. To heat the system from 0 to 300 K, we incrementally added kinetic energy for a total of 30 ps while implementing decreasing constraint levels in the same manner as the described minimization protocol. Using QM/MM, we equilibrated the system at 300 K for 500 ps with zero applied constraints. This resulted in an energetically and structurally stable system.

Transition Path Sampling

We designated the initial and final states of the reaction by implementing the following order parameters: chemical species of the enzymatic reaction with a hydride–donor distance less than or equal to 1.5 Å and a hydride–acceptor distance greater than or equal to 1.5 Å were considered part of the reactant (dihydrofolate) basin, whereas species with a hydride–donor distance greater than or equal to 1.5 Å and a hydride–acceptor distance less than or equal to 1.5 Å were designated as part of the product (tetrahydrofolate) basin. Following the next step of the TPS algorithm, we connected the reactant and product basins via an initial, biased QM/MM trajectory of 250 fs for implementation of the CHARMM command RESD with the parameter that the hydride–acceptor distance was constrained to 1.25 Å by a harmonic force constant of 60 kcal mol^–1 Å^–1.

Using this initial constrained trajectory, we selected a random point of integration, or time slice, along the trajectory and perturbed the momentum of each atom in the system by adding a random value as determined by selection from a zero-mean Gaussian distribution multiplied by a scaling factor of 0.2. After rescaling these new momenta to conserve total energy and eliminate any net angular or linear momenta, we propagated the system both forward and backward for 250 fs in time to generate a resultant trajectory of 500 fs in total length. We utilized this process of randomly, iteratively perturbed time slices until we achieved an ensemble of 230 reactive or QM/MM trajectories that connected both designated configuration basins. We maintained a ratio of reactive to nonreactive trajectories (acceptance ratio) of approximately 25%. To ensure complete decorrelation from the original constrained reactive trajectory, we disregarded the first 30 generated trajectories in all of our analyses.

Committor Calculations

To determine the commitment probability^28,36 of a specific set of coordinates corresponding to a particular time slice along a reactive trajectory, we reinitialized the QM/MM dynamics at this point using random velocities derived from a Boltzmann distribution. All committors for individual time slices were calculated using 50 trajectories of 250 fs each. We considered the value of the number of these trajectories landing in the product basin divided by the total number of trajectories generated to be representative of the committor value of the time slice. In this respect, a point with a committor value of 1 would have a 100% chance of reaching the product basin, whereas a set of atomic coordinates and velocities with a committor of 0.5 would be equivalent to the transition state.

To determine the level to which a specific degree of freedom was necessary for the transition state formation of the enzymatic reactions of hsDHFR and ecDHFR, we conducted committor distribution analyses.^28,36 Using a transition state as the starting point, we conducted QM/MM simulations for a trajectory 1 ps in length while constraining the atoms of interest with a harmonic force constant of 2000 kcal mol^–1 Å^–1. For all constraints relevant to the atoms of the protein, we constrained with regard to both the hydride donor and acceptor and the β-carbon of the specific residues (α-carbon in the case of glycine). We calculated the committor value for every 50th slice of this constrained trajectory, giving 20 committor values for each transition state. For each committor distribution presented in this study, we used three transition states as starter points.

Kernel Principal Component Analysis

In principal component analysis (PCA), one must first determine the eigenvectors of the correlation matrix of the data; then, the variance of the data along these eigenvectors is proportional to the corresponding eigenvalues. If the eigenvalues of the first few eigenvectors are dominant, then they form a low-dimensional representation of the data. The limitation of PCA is that it implicitly linearizes data, which is not a good approximation for the distribution of transition states on the separatrix. To correct for the linearization assumption, we used kernel PCA (kPCA). In kPCA, a nonlinear transformation of the original data is made to a space where the PCA is valid, PCA is performed there, and then the results are transformed back to the original space. We found that quadratic polynomial transformation (XY)² led to the first eigenvector dominating the variance. The direction of the reaction coordinate is perpendicular to the separatrix; therefore, we found the residues that contributed the least to this dominant eigenvector. These residues are good candidates for contributing to the reaction coordinate.

Notably, all calculation methods and parameters reproduced the data from our original ecDHFR study to ensure that direct comparisons are appropriate.

Results

Identification of a PV in the Reaction Coordinate of hsDHFR

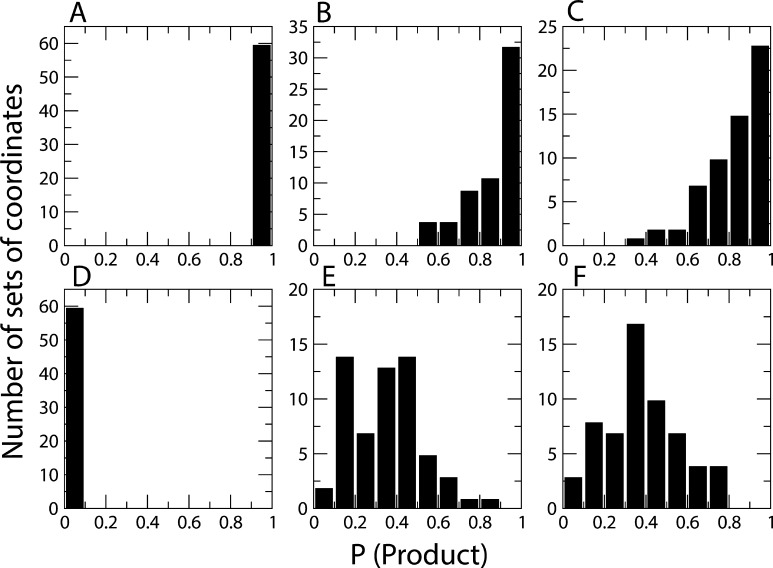
We utilized committor distribution analysis^28,36 to study the reaction coordinate of hsDHFR in comparison with that of ecDHFR. Committor distribution for an enzyme-catalyzed reaction is a rigorous computational method that is utilized to deduce the complete enzymatic reaction coordinate.³⁷⁻³⁹ The first step in this analysis is to use the coordinates of an extant transition state to initiate a constrained QM/MM trajectory. If the correct set of reaction coordinate variables is constrained, the resultant trajectory will remain on the separatrix. The next step is to run committor analysis using points along this new constrained trajectory to obtain a distribution of committor values. A correct selection of relevant degrees of freedom would yield a distribution peak at 0.5. Because of the complexity of the enzymatic reactions and the statistical nature of the calculation, it is expected that selection of an accurate enzymatic reaction coordinate will yield a broad distribution centered at 0.5. Incorrect selections of the reaction coordinate in an enzymatic system will generally result in distributions with a peak far from the 0.5 committor value.^37,39

Using this analysis, we found that a subpicosecond protein motion is dynamically coupled to the reaction catalyzed by hsDHFR. Committor distribution analysis is used to determine what motions are on the dividing surface (the stochastic separatrix), and what motions are orthogonal to it. The term dynamic coupling refers to degrees of freedom that are part of the reaction coordinate and occur on the same time scale as barrier passage. In other words, the promoting vibration modulates the barrier and does so on a time scale that is comparable to passage over the barrier (i.e., they are not adiabatically separable).

We observed that the minimal definition of the hsDHFR reaction coordinate required the inclusion of the positions of the following residues: I17, 24-PWPPLRNE-31, F32, F35, and 62-PEKN-65 (Figure 1). The residues 24-PWPPLRNE-31 include the PWPP modification of the Met20 loop; F32 and 62-PEKN-65 also correspond to previously reported PCEs in the DHFR protein family.²⁷ Evolutionarily analogous residues in ecDHFR (I14, 21-PWNLPAD-27, F31, and G51) were not part of the ecDHFR reaction coordinate. Figure 2 shows select committor distributions generated for both the hsDHFR and ecDHFR systems. To create each distribution, we utilized three transition states as starting points for the production of three constrained QM/MM trajectories 1 ps in length. We performed committor analysis on every 50th time slice of each new trajectory to obtain a set of committor values. We performed calculations while implementing constraints on the following variables: (1) the hydride–donor and hydride–acceptor distances (ecDHFR, Figure 2A; hsDHFR, Figure 2D), (2) the positions of the atoms for NADPH and dihydrofolate ligands (ecDHFR, Figure 2B; hsDHFR, Figure 2E), and (3) the positions of the ligand atoms in addition to the distances between the β-carbons (α-carbon in the case of glycine) of the putative PV residues and the hydride donor and acceptor (ecDHFR, Figure 2C; hsDHFR, Figure 2E).

Figure 2.

Histograms of committor distributions obtained with increasing numbers of constraints for the ecDHFR and hsDHFR systems. Graphs (A), (B), and (C) correspond to ecDHFR, whereas (D), (E), and (F) pertain to the hsDHFR system. Data shown in (A) and (D) were obtained while constraining only the distances between the hydride and the donor and acceptor, (B) and (E) illustrate the results of the committor distribution calculation while applying constraints to all atoms of the ligands, and (C) and (F) represent data derived while constraining the residues of the putative PV (I14, 21-PWNLPAD-27, F31, and G51 in ecDHFR; I17, 24-PWPPLRNE-31, F32, F35, and 62-PEKN-65 in hsDHFR).

In the hsDHFR system, increasing the number of constraints resulted in a committor distribution that peaked close to 0.5. Additionally, the incorporation of protein constraints was essential for achieving an adequate description of the hsDHFR enzymatic reaction coordinate. All of the distributions calculated for ecDHFR are centered far from 0.5, demonstrating that the constraints tested were not sufficient approximations of the enzymatic reaction coordinate. When only the atomic positions of the ligands were constrained, hsDHFR exhibited a marked improvement in the centering of the committor distribution, whereas ecDHFR did not. Because the ligands interact with a large portion of the protein in both DHFR systems, it is likely that constraining these atoms resulted in a general constraint on protein conformation. The gradual transition to a distribution that peaked closer to 0.5 suggests that the reaction coordinate in the hsDHFR system is a wider tube in configuration space (i.e., in protein structure). It must be reiterated that these differences are qualitative; however, it is clear that there are basic physical differences captured by the variation between panels C and F of Figure 2. It is also possible that there is a set of protein constraints that would imply direct coupling of ecDHFR protein motions to hydride transfer, but given the preponderance of evidence, that seems highly unlikely.

Disparities in Transition Path and Transition State Variation between ecDHFR and hsDHFR

We observed an increase in structural variation of the transition states in the TSE of hsDHFR when compared to those sampled by ecDHFR. First, we calculated the RMSD values for the position of only the ligand atoms at each transition state versus those of the average transition state to be 0.0779 and 0.221 Å in ecDHFR and hsDHFR, respectively. We then used the atomistic structures of the transition state conformations of the protein to perform this calculation and obtained RMSD values of 0.0594 and 0.154 Å for the transition state conformations of ecDHFR and hsDHFR, respectively. We also observed an increase in variation of the donor–hydride–acceptor angle at the transition state in hsDHFR compared to that of ecDHFR. Although the average value for this angle was similar for both enzymatic systems (151.92° and 151.00° in ecDHFR and hsDHFR, respectively), the standard deviation for this angle was greater in the human enzyme (3.2° and 73° in ecDHFR and hsDHFR, respectively). It is important to note that these RMSD values must be considered qualitative measures of transition state variation.

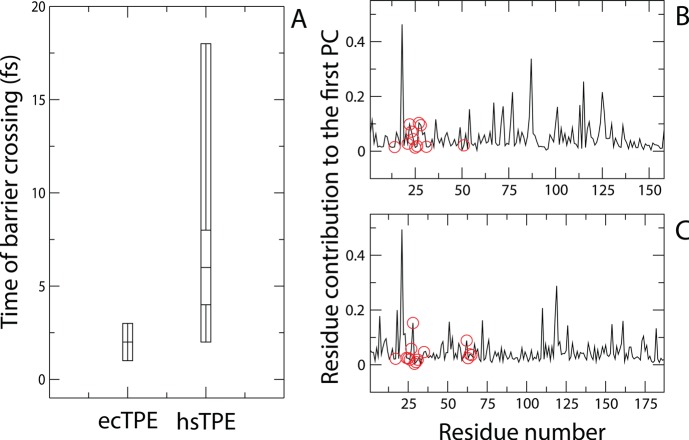
We also detected increased variability in the times of barrier crossing for the hsDHFR TPE in comparison to those calculated for the ecDHFR TPE. Figure 3A shows box plots representing the distributions of barrier crossing times exhibited by both the ecDHFR and hsDHFR systems. In ecDHFR, the distribution of committors calculated has a breadth of only 2 fs, whereas the corresponding distribution for the hsDHFR system spans 17 fs. These distribution differences are associated with a p value of less than or equal to 0.05. This result may be indicative of an increase in the ruggedness of the free energy landscape of the hsDHFR reaction compared to that of the reaction catalyzed by ecDHFR. The E. coli enzyme is clearly a much stronger funnel to a single path through the reactive phase space. These results demonstrate that the evolutionary changes allow for greater variation in paths through the reactive phase space in hsDHFR compared to that of the prokaryotic enzyme. Although it is unclear what exactly this may confer biologically, the physical observation is definitive. We can only speculate that this greater chemical path flexibility may allow for greater responsiveness to the variable chemical environments found in eukaryotic systems.

Figure 3.

Representations of changes in the TPEs and TSEs from ecDHFR to hsDHFR. (A) Box plots illustrating the differences in the distributions of barrier crossing times for the ecDHFR TPE (ecTPE) and hsDHFR TPE (hsTPE). Each distribution was calculated using barrier crossing times from 21 representative trajectories in each TPE. For the ecTPE, the shortest and longest times of barrier crossing were 1 and 3 fs, respectively. The values for the 2nd quartile, median, and 4th quartile were all 2 fs. In the hsTPE, the corresponding values were as follows: shortest time = 2 fs, 2nd quartile = 4 fs, median = 6 fs, 4th quartile = 8 fs, and the longest time = 18 fs. (B) kPCA calculation for the ecDHFR TSE, with putative PV residues at positions 14, 21–27, 31, and 51 indicated with red circles. (C) kPCA calculation for the hsDHFR TSE, with putative PV residues at positions 17, 24–31, 35, and 62–65 indicated with red circles.

To determine the contribution of the position of each residue to the variance in the hsDHFR and ecDHFR TSEs, we conducted kernel principal component analysis.⁴⁰ This technique presents a way to perform orthogonal transformation of a multidimensional surface, such as TSE, through nonlinear kernels. We have previously used this technique as a way to identify PV residues in the enzymatic reaction coordinate of human heart lactate dehydrogenase (LDH).³⁸ In LDH, the residues contributing the least to the first principal component (PC) were able to adequately approximate the enzymatic reaction coordinate. The results of this calculation for the ecDHFR TPE and hsDHFR TPE are displayed in Figure 3B and 3C, respectively. The residues of the putative PV are highlighted with red circles (I14, 21-PWNLPAD-27, F31, and G51 in ecDHFR; I17, 24-PWPPLRNE-31, F32, F35, and 62-PEKN-65 in hsDHFR). In hsDHFR, all but two of the PV residues corresponded to minima along the first PC, whereas the majority of these residues in ecDHFR did not.

Active Site Structural Differences in the Relevant hsDHFR PV

We found that a compressive motion between residues I17 and P35 correlates with a dynamic decrease in the hydride donor–acceptor distance and with the time of barrier crossing in the hsDHFR system. Figure 4 shows the time series representing specific dynamic distances during an exemplary trajectory along with the moment of chemical barrier passage (gray region: 354–361 fs). Breaking of the hydride–donor bond (red) and formation of the hydride–acceptor bond (blue) are shown in Figure 4A along with the donor–acceptor distance during the reaction (black). Figure 4B is a representation of specific distances between different aspects of the protein during the same example trajectory. The compression between I17 and P35 (orange) coincides with a smaller compressive fluctuation between I17 and the hydride acceptor (violet) following an excursion of P24 toward I17 (green). This fast motion of P24 toward I17 is the result of a density fluctuation propagating through the protein bulk, which was also the case for the previously identified PV in the reaction coordinate of human heart lactate dehydrogenase.²¹

Figure 4.

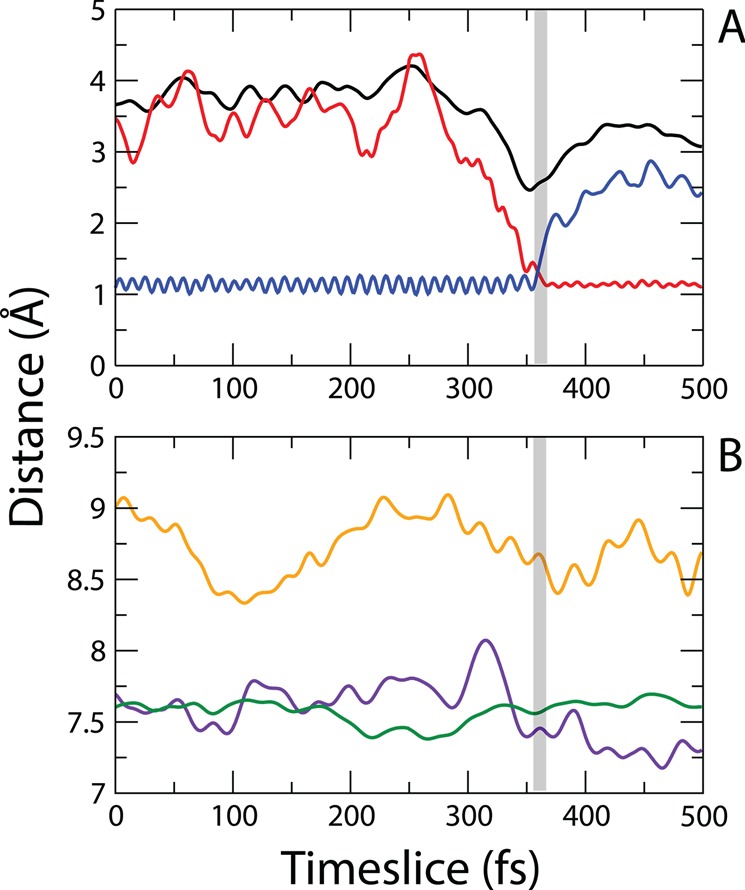
Distance time series of an exemplary reactive trajectory illustrating the dynamic contributions of specific residues to chemical barrier passage in hsDHFR. (A) Distances corresponding to the chemical reaction (red = hydride–acceptor, blue = hydride–donor, and black = donor–acceptor). (B) Dynamic distances within the protein (orange = I17(atom HE1)–F35(atom HD1), violet = I17(atom CB)–acceptor, and green = P24(atom CB)–I17(atom CB)). The gray region represents the time of barrier passage for this specific trajectory (354–361 fs).

We detected subtle structural changes between the active sites of ecDHFR and hsDHFR, which establish a physical link between the hydride donor–acceptor axis and the PV residues in hsDHFR. Figure 5 shows the position of PV residues near the active site in relation to the hydride donor–acceptor axis for both hsDHFR and ecDHFR. In hsDHFR, the hinges of the Met20 loop, P24 and G31, come into direct contact with I17 and F35, respectively, and these two amino acids are ideally situated on either end of the hydride donor–acceptor axis. The active site of ecDHFR is too loosely packed to support these specific contacts. In particular, the close van der Waals interaction between I17 and P24 in hsDHFR is not pronounced in the analogous residues of ecDHFR (I14 and P21). Tighter packing of the hsDHFR active site may be an important enabling factor for the incorporation of fast protein dynamics in the hsDHFR reaction coordinate.

Figure 5.

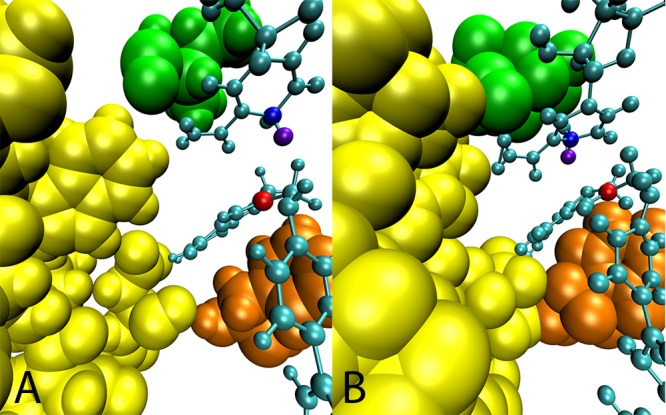
Structural differences between the ecDHFR and hsDHFR active sites. View of the equilibrated structure of the (A) ecDHFR and (B) hsDHFR system. The ligands are cyan, the hydrides are violet, the hydride donors are blue, and the hydride acceptors are red. Residues of the Met20 loop are yellow, I14/17 is green, and residue F31/35 is orange.

Discussion

The committor distribution analysis data presented here represent our best attempt at isolating the reaction coordinate of hsDHFR. We tried many combinations of candidate residues based on the kPCA output. Incorporating residues that also corresponded to important mutational events was key to our elucidation of the reaction coordinate. Even using kPCA guidance, elucidation of the reaction coordinate to the accuracy we obtained took many months of computer time.

We show that the subpicosecond protein motion in a specific set of residues is dynamically coupled to the reaction coordinate of hsDHFR. This conclusion is strongly supported by the results of our committor distribution analysis. Contradistinctively, there is no indication of a PV in the enzymatic reaction coordinate of ecDHFR, suggesting a change in the form of catalysis from the E. coli to human enzyme. It could be possible to experimentally validate this finding through kinetic studies of enzymes that are expressed utilizing heavy-isotope substitution throughout the protein matrix.⁴¹ If a PV is in fact dynamically coupled to the enzymatic reaction coordinate, a “heavy” enzyme would exhibit a decreased probability of barrier crossing, which would not be the case if there was no such coupling. This type of experiment is a possible candidate for future work.

Experimental²⁴ and theoretical⁴² evidence indicates that the enzymatic rate enhancement of ecDHFR is primarily governed by electrostatic effects, but electrostatics do not appear to be the sole factor responsible for catalysis in hsDHFR. As one of the key mutations differentiating ecDHFR from hsDHFR, PWPP modification of the Met20 loop has been implicated in electrostatic stabilization of the transition state for the ecDHFR-catalyzed hydride transfer reaction,¹² and the presence of this modification in a chimera E. coli enzyme results in a decreased hydride transfer rate.²⁷ Concurrent with this modification hindering the electrostatic-based catalysis of ecDHFR, this mutational event also led to a change in the conformational states of hsDHFR and a more tightly packed active site.^27,26 Combined with the other mutational events that separate the E. coli and human enzymes, this alteration of the Met20 loop allows for a mechanism of catalysis in the hsDHFR that includes rapid protein dynamics or a PV.

We also found that the stochastic separatrix, or TPE, of the ecDHFR-catalyzed reaction is more narrow in terms of the geometry of the transition state structures and the variability of reactive conformations as compared to the enzymatic reaction of hsDHFR. This finding is in agreement with our committor distribution results demonstrating a smaller degree of tolerance for changes in the enzymatic conformation of ecDHFR relative to hsDHFR in order to remain on the separatrix. Our inability to identify a definitive reaction coordinate for the ecDHFR-catalyzed reaction also indicates that perturbation of the ecDHFR transition state structure is more likely to result in deviation from the separatrix compared to doing so with the human enzyme. When considered within the context of the conformational landscape model of enzymatic reactions,^1,43,44 these results suggest that fast distance sampling along the reaction coordinate indicative of a PV could introduce a degree of finely grained ruggedness to the free energy landscape of an enzymatic reaction. Thus, it can be argued that dynamic coupling of protein motion to the reaction coordinate increases the likelihood of barrier crossing by decreasing the need for an optimal electrostatic and geometric arrangement of the active site. As an extension of this conclusion, the breadth of possible reactive conformations corresponding to a specific conformational basin appears to be greater for the hsDHFR enzymatic system than for the ecDHFR system.

An almost philosophical question relates to the selective pressure that caused such exquisite design of active sites when the chemistry is almost never rate limiting. This is a conundrum for enzymatic active sites in general, not just promoting vibrations. The results of this study indicate that possible selective pressure on the protein matrix, which was likely optimized after a static active site, was robustness to multiple phase space paths rather than optimization of the chemical rate, although this is purely speculation. Further work is needed to elucidate possible evolutionary pressures for enzymatic promoting vibrations.

The authors declare no competing financial interest.