Calibration for medium resolution off-axis electron holography using a flexible dual-lens imaging system in a JEOL ARM 200F microscope

Abstract

In this work the calibration of a medium resolution off-axis electron holography using a dual-lens imaging system in a JEOL ARM 200F is shown. The objective dual-lens configuration allows adjusting the field of view from 35 nm to 2.5 μm. Subsequently, the parameters used in phase shift reconstruction were calibrated considering biprism voltage versus fringe spacing (σ) and versus fringe width (W). The reliability of the transmission electron microscope performance using these parameters was achieved using gold nanoparticles of known size and adjusting the excitation voltage of the lenses.

1. Introduction

About two decades have passed since the introduction of aberration-corrected electron microscopy [1]. The ease of use of the improved atomic resolution became almost instantly a must for a large number of discoveries in nanotechnology, and thus the use of aberration corrected microscopy and related publications in nanotechnology have risen in parallel. As an initially unnoticed side effect, an equivalent technology jump has occurred in electron holography. The quality of electron holograms and the corresponding attainable reconstructed phase resolution is mainly improved by a high coherence of beam importantly improved in the field emission gun (FEG) instruments [2-3]. However, scientific contributions in the area of electron holography have not shown a corresponding consequential growth. Instead, the number of publications over the past two decades has fluctuated but overall remains constant. One of the key reasons for the lack of an increase in the use of the holographic technique is the absence of dedicated electron holography instruments (i.e.: a machine in which magnification of the sample can be varied without having to re-align the microscope). Additionally the necessary modifications to the optical settings of any conventional transmission electron microscope for holography are manual and time consuming and are incompatible with its standard optical settings. Thus the optical state for a holography setting remains difficult to reproduce and even uncalibrated in the sense that the effective magnification remains to be determined by the user on each occasion.

In this work we report and describe a reproducible routine for variable magnifications in off-axis electron holography using the flexible dual-lens system in a JEOL JEM ARM 200F. The method to be described allows a calibrated setup for predefine FOV ranging from 35 nm to 2500 nm, ideal for the characterization of materials in nanotechnology from where we can extract quantitative information such as, e.g., electrostatic fields [4-9], magnetic fields [10-16], non-stained biological samples [17-18], determination of the thickness and surface morphology in nanostructured materials [19-21], dopant profiles and strain measurement in semiconductor technology [22-29]. New developments in improving the reconstructed phase and to avoid Frensel fringes can be obtained by novel configurations as the double or triple biprims in the microscope as well as a modified Lorentz conditions by controlling the diffraction lens in the microscope [30-32].

2. Electron optics in off-axis electron holography

Transmission Electron Microscopy (TEM) can be best explained in terms of wave optics due to the wave-like behavior of electrons. An incident plane wave coming from the highly-coherent field emission electron source interacts with the sample. The transmitted electrons though the specimen are considered as the object exit wave, which contains key physical information about the sample. During the image formation process the intensity of the image is recorded (I = |ψ|²), the projected image contains information about the spatial distribution of the atoms into the sample; however, other contributions in the sample such as: electrostatic and magnetostatic external fields cannot be recovered from the direct intensity measurement. In this way, interferometry methods are a good solution for this phase recovery [26].

Electron holography is an interferometric technique possible to extract the amplitude and phase. Thus in electron holography two wavefronts interfere, one acting as a reference wave and the other as the object wave, as shown in Fig. 1., both waves are recorded on a dedicated sensor to produce an interferogram or hologram. In off-axis electron holography and the optical setup used in this paper (see Fig. 1) the object wave is defined as the electron wavefront passing through the sample and the reference wave is defined as the electron wavefront passing through nearby vacuum media. In off-axis electron holography, a specimen is located such that it does not fill completely the image plane as in the sketch of Fig. 1, thus only part of the electron wavefront passes through the specimen, the other part passes through the same nearby vacuum media as the reference beam. An electrostatic biprism is biased in order to combine the object and reference waves which overlap at an angle creating an interferogram that contains information about the amplitude and optical phase of the object. In this case the interferogram is also called a digital holographic interferogram, or hologram, with a characteristic width and fringe spacing. The interferometric process to achieve a high quality hologram is described as follow: There are four critical parameters that need to be considered to obtain high quality holograms: the width (W) of the interference fringes which determines the FOV, the fringe spacing (σ) that determines the lateral spatial hologram resolution, the fringe contrast and the electron dose which determines the phase noise or phase sensitivity. Fringe contrast is a parameter that defines the quality of a high-resolved phase. In this case the recording media (i.e. charge-coupled device (CCD) camera) of the holograms plays also an important role in the phase reconstruction, high dynamic ranges are directly related to the number of electrons detectable leading significant improvement in the fringe contrast and as a consequence a better signal to noise ratio in the reconstructed phase images [33-35].

Fig. 1.

Off-axis electron holography beam diagram

After the acquisition, the holograms are numerically analyzed to extract the amplitude and the phase of the image. After passing through the biprism the two waves interfere at the image plane, which is the location where the CCD sensor is, with an intensity given by [32],

$$I\left(\overrightarrow{r}\right)={\mid {\psi }_r+{\psi }_0\mid }^2=1+A_o{\left(\overrightarrow{r}\right)}^2+2A_o\left(\overrightarrow{r}\right)\cos (2\pi \Delta \overrightarrow{q}\cdot \overrightarrow{r}-{\phi }_o\left(\overrightarrow{r}\right))$$ (1)

As we describe above, $I\left(\overrightarrow{r}\right)$ contains information about both the object phase and amplitude, Where $A_0\left(\overrightarrow{r}\right)$ and ${\phi }_0\left(\overrightarrow{r}\right)$ are the amplitude and phase of the exit object wavefront, respectively, both of them are spatial coordinate dependents. The hologram is analyzed by the Fast Fourier Transform (FFT) given by,

$$\mathcal{F}\left(I\left(\overrightarrow{r}\right)\right)=\delta \left(\overrightarrow{k}\right)+\mathcal{F}\left(A_o{\left(\overrightarrow{r}\right)}^2\right)+\delta (\overrightarrow{k}+\Delta \overrightarrow{q})\ast \mathcal{F}\left(A_o\left(\overrightarrow{r}\right)e^{i{\varphi }_o\left(\overrightarrow{r}\right)}\right)+\delta (\overrightarrow{k}-\Delta \overrightarrow{q})\ast \mathcal{F}\left(A_o\left(\overrightarrow{r}\right)e^{-i{\varphi }_o\left(\overrightarrow{r}\right)}\right)$$ (2)

The terms in Eq. 4 are interpreted as follows: the first term corresponds to the contribution of electrons propagated without being affected by the sample, which is the contribution of the reference wave with amplitude 1. The second term corresponds to the standard non-holographic object image intensity. The third and fourth terms contain the phase and the amplitude of the wave, which can be recovered by the inverse Fourier transform taking one of the two last terms of the equation (2). These two terms in the Eq. (2) are called sidebands and they are complex conjugate terms one from each other. One of these two side bands of the FFT is spatially filtered and its inverse FFT can be computed to recover the phase and amplitude of the wave. The resulting reconstructed hologram is now displayed as a phase map that contains the data corresponding to the phase and amplitude of the object exit wavefront when compared to the plane reference wavefront whose phase is known. The phase map is said to be wrapped since it contains gray scale contours that have phase jumps with a period of 2 π. In order to fully quantify the phase map obtained from the inverse FFT, a procedure is followed to unwrap the phase to have a continuous phase map. There are a wide variety of commercial and home-made algorithms that can deal with the unwrapping [26,33]. The choice depends on the complexity and signal to noise ratio of the phase map. The aim of all the algorithms is rendered a smooth unwrapped phase map that will ease the quantification of the object optical phase and amplitude. In this work the phase unwrapping process was obtained by using HoloWorks v5.0.4 algorithm [33-34].

3. Experimental procedure

In previous work we have calibrated the dual-lens imaging system for one specific FOV, fixing the OL at 5.5V, in order to extract morphological information such as surface discontinuities and irregularities in gold decahedral nanoparticle surface [21]. Now, we are reporting the calibration of the whole range of operation for this instrument under dual-lens mode. The conventional setup for off-axis electron holography can be thought of as consisting of three parts, an illumination system, an imaging system, and a projection system [4]. For the microscope used, the illumination system consists of three condenser lenses C1, C2, and minilens (CM). The imaging system consists of two lenses: OL and OM coupled with an electron biprism, which is placed near the first image plane of the selected area aperture. The imaging operation consists of a virtual image formed by the objective lens and a real image formed in a fixed imaging plane by the objective minilens. The final virtual source position is the imaging position at the second focal point of the first lens through the second lens. A critical parameter for a variable field of view in this flexible dual-lens system is mainly the objective lens value which sets the magnification. In our configuration we have an additional objective minilens, which is used basically to adjust in a fine form the focus of the sample. Another important lens value is the projector lenses, which also has been changed sequentially to evaluate our FOV. Finally the crucial variable in electron holography is the biprism voltage (V_b), which determines the fringe spacing that is related to the spatial resolution and the illumination which determine the fringe contrast, which determine the phase resolution or “noise” described in previous section. The electron biprism consists of a 0.5–0.6 μm diameter platinum wire and an external DC voltage source that can provide a maximum output voltage of 320V. Below the imaging system, there is a projection system formed with 3 intermediate lenses and a projector lens which normally provide the proper image size (magnification) for the recording media. The microscope was operated at non-standard lens excitation, with C1 maximized and CM set to zero in order to increase the coherence of the electron beam by using an elliptical illumination. Then the first intermediate lens is set to zero. Under these operating conditions the projection system no longer provide enough magnification; however, additional magnification may be achieved by using the 2k × 2k GIF (Gatan Image Filter) camera that is located at the very bottom of the column.

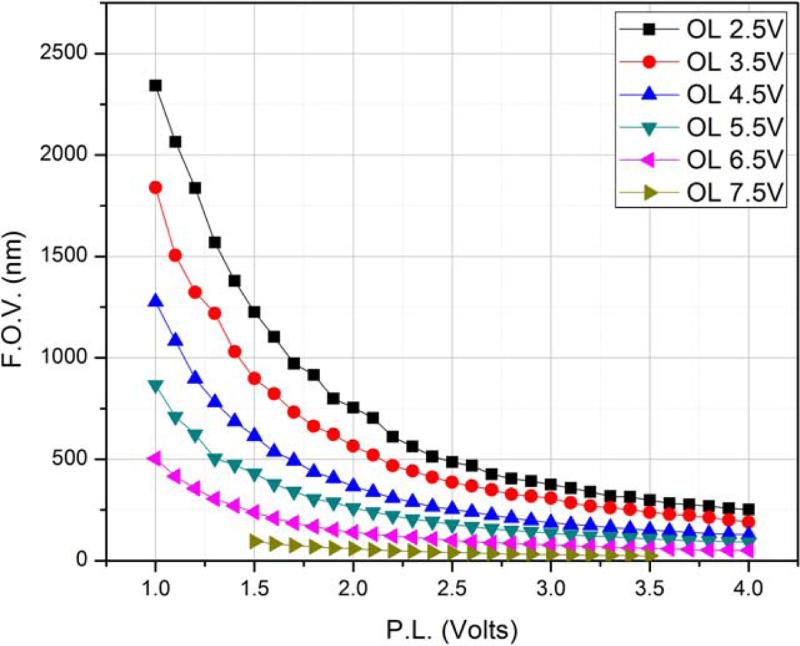
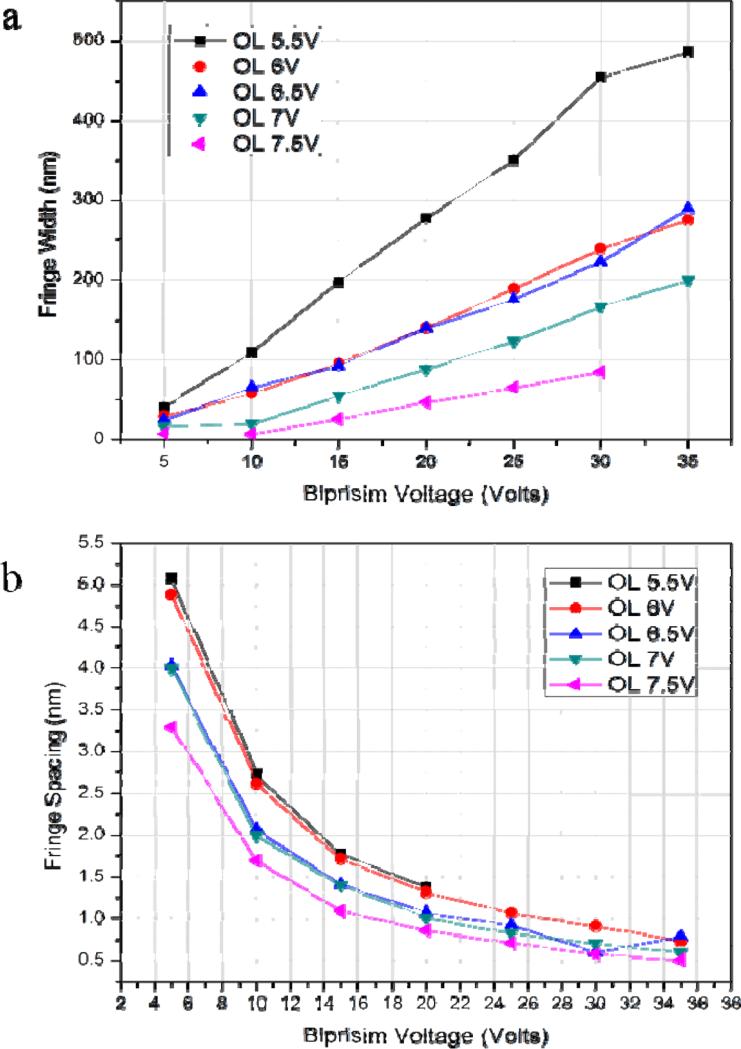
The procedure described in this work is a reproducible and reliable method for predefined field of views and could be used to characterize nanostructured materials of a wide range of size. The remanent hysteresis in the lenses of the microscope can be eliminated by a lens relaxation process applied previous to the experimental work. The dual-lens imaging system allows a variable magnification providing a wide range for the field of view. The calibration was achieved using gold nanoparticles of known size, a regular TEM image was recorded at different magnifications and it is used as calibration standard for the settings of the dual lens with different excitation in the. Using the dual-lens mode the image recorded needs to be recalibrated. In our configuration the GIF camera was used to collect the images using as the reference a gold particle taken in conventional TEM mode. In the top box of the Fig. 2, the calibrated image is registered and the particle size is measured. The first parameter to set in the microscope is the voltage of the main objective lens (OL) and it changes sequentially from 1 to 7.5 volts in steps of 0.5V. Once fixed the main OL value a fine focus adjustment by using the objective minilens can be done, which does not affect the FOV of the region of interest or the fringe contrast. The adjustment of the field of view was reached by changing the projector lens values, which has been plotted in the Fig. 3. It is important remark that the FOV can vary from tens of nanometers up to more than 2 microns, basically assuming that low OL values will be used for large FOVs and high OL values to nanometric scale less than 1 micron as can be observe in the tendency of the curves shown in Fig. 3. The interference fringes from the biprism were registered under the same lens values and using the width fringes in the maximum possible FOV recorded in the GIF camera. Therefore, the interference width and fringe spacing were determined and also graphed in the Fig. 4. In the Fig. 4a the fringe width versus biprism voltage is plotted, which has been adjusted in the whole area of the CCD camera. As complementary information the fringe spacing is graphically reported in the Fig. 4b also obtained versus the biprism voltages. In both figures 4a and 4b, the fringe quality number can be extracted and it has been listed in the last column of the Fig. 2. Experimental parameters FOV, fringe width (W) and fringe spacing (σ) for the different OL values are also included in the columns 4. All reference holograms included in the 3^rd column of the Fig. 2 were recorded at 15V.

Fig. 2.

Calibration chart of the FOV using the GIF camera and their corresponding interference width and fringe spacing under fixed PL and V_b values at different OL voltages.

Fig. 3.

FOV (nm) versus PL voltages at different OL excitation voltages.

Fig. 4.

(a)Fringe width (W) and (b)fringe spacing(σ) versus biprism voltage (V_b).

A fine tuning over the final hologram can be done by continuously altering some lenses such as CL3, OM and PL keeping the interference pattern with no important alterations and producing a fringe contrast fairly stable. A variation in CL3 results in a variation of the fringe contrast; all the values reported in the Table 1 have been taken with the optimum fringe contrast, which ranges from 15 to 30 %. The OM variation is not reflected in the quality of the hologram and the reconstructed phase. PL lens is fixed at the beginning of our experiment since it is crucial in the definition of the FOV and the fine tuning can be applied to adjust the fringe width in the FOV without affecting the quality of the hologram. In the Fig. 2 the fourth column shows the fringe quality number, which is important in the calibration process [22]. In this way, a summary of the work done for each lens is presented in the Table 1 using hexadecimal notation. The lenses values are the optimal conditions for the acquisition of high quality holograms for different FOV's at fixed biprism voltages, both included in Table 1 as well.

Table 1.

Optimum conditions for the Low Mag dual lens imaging system (The values of each lens is given in hexadecimal notation).

OL (volts)	1	2	2.5	3	3.5	4	4.5	5	5.5	6	6.5	7	7.5
CL1	6600	6600	6600	6600	6600	6600	6600	6600	6600	6600	6600	6600	6600
CL3	8EF0	9033	9033	BF13	8DA3	8E27	8DFA	8DFA	8DE0	8DB0	8FB6	8F36	8ED4
OL-C	2020	3A20	4735	5465	616E	6EAE	7BEE	88FE	961E	A333	B088	BD3E	CB8E
OM	BDE8	BF03	BF08	BDE8	BEF7	BEC0	BDD5	BD62	BACC	B9A8	B66C	B0FF	9F0E
IL2	9FFF	F210	F210	FBAF	FBAF	FBAF	FBAF	FBAF	FBAF	FBAF	FBAF	FBAF	FBAF
IL3	54A0	54A0	54A0	54A0	54A0	54A0	54A0	54A0	54A0	54A0	54A0	54A0	54A0
PL	85E0	85E0	9104	8C14	921F	9147	9430	8541	7DCC	7B71	83C1	716F	716F
Vb (volts)	21	19	19	17	19	19	16	20	22	27	23	39	37
FOV (nm)	1000	550	430	400	330	295	230	224	191	156	95	85	58

4. Results

The whole FOV range from 1-7 volts in OL was investigated and the images are available in the supplementary information (SI) described as follow: In order to have sufficient flexibility in the dual-lens system it is necessary to work using the low magnification mode. In this way, values of the OL can be changed systematically to calibrate the settings of the microscope. The first step to calibrate the electron holography system is to setup for different magnifications which are determined by the excitation voltage of the OL. Since the projector lens plays the main role in the FOV calibration, the FOV versus PL values were plotted for each OL excitation voltage. The corresponding graph is shown in Fig. 3. PL values range from 1 to 4 volts, in small steps 0.1V, with the smallest FOV for the largest OL values (e.g., 7.5V). Values from 1 to 7.5 volts in the OL were optimized with different voltages of the biprism (0 to 35V), the criterion of the optimization has been taken considering a minimum fringe contrast of 15% and filling the interference width to the FOV into the CCD. As a result of the calibration the fringe with and fringe spacing ranges are obtained and shown in figures 4a-b. Fringe width, fringe spacing and fringe contrast are described by the equation reported by Wang et al [4,22]. It can be observed from the behavior of the curves presented in Fig. 3 and 4 that at a fixed OL value, i.e. 7.5 V at a V_b = 20 V an interference width around 50-55 nm with high fringe contrast (30% from Fig. 5) is shown, that remains unchanged for PL values from 1.5-2.5 Volts.

Fig. 5.

Biprism holograms at different voltages: (a) 10 V, (b) 15V, (c) 20V and (d) 25V. (e) Fringe contrast versus biprism voltage at different fixed V_OL.

Using holograms with no object, called reference holograms, allows to obtain fringe contrast percentages as a function of the biprism voltage for all OL values. In Fig. 5a-d, reference images of the biprism were taken with values from 10 to 25 V in increments of 5 V. The fringe contrast percentage is plotted versus biprism voltage in the Fig. 5e. An optimized fringe contrast will result in a wide dynamic range values to obtain better phase resolution, which are related to the feasibility to extract information from the mean inner potential projected in the hologram. This wide range of gray scale values calls for a CCD camera sensor with large dynamic range. Higher fringe contrast may be achieved by using astigmatic illumination, this is an artifact that allows more coherence in one direction, but reduces the illumination. In the metallic nanoparticles included in the SI we have analyzed two types of particles: 1) gold decahedral nanoparticles and 2) Au@Pd core shell nanocubes. In the case of the gold particle we have shown superficial irregularities in the particles [21]. In the case of the core shell particle we show different reconstructed phases as function of the zone axis orientation of the faceted nanocubes, Fig. S2 and S3.

In table 2, we present a comparison of the operation ranges for different microscopes using the same dual lens imaging mode reported before in [4,22]. In these references the calibration were carried out for large field of views. In our work we are presenting shorter and larger FOVs than these references. Some difference in the available working ranges are observed, but the main difference would be at the operation procedure due to each instrument configuration. In the configuration reported in this work, the flexibility of lens manipulation is an alternative setup which can also be done to work under Lorentz conditions with a control of the diffraction lens in order to improve the phase and lateral resolution as reported in the reference [32] and which can be considered as future work.

Table 2.

Comparison between different microscopes using dual lens imaging system.

Microscope	Fringe Width	Fringe Spacing
JEOL ARM 200F	35-2,500 nm	0.5-5.5 nm
4 JEOL 2010F	50-1400 nm	0.8-7.5 nm
22 FEI Titan	700-900 nm	4-6 nm
	100-200 nm	0.5-1 nm

5. Conclusion

The reconstruction phase of the metallic nanoparticles included in this work shows the optimized parameters for off-axis electron holography in a JEOL ARM200F microscope using dual-lens mode, included in the SI. The calibration provides the optimal conditions for a wide range of field of view using different objective lens excitation and biprism bias voltages. The calibration of the parameters were achieved by using a gold nanoparticle of known size, in this way we report the interference width, fringe spacing and fringe contrast. The current calibration provides suitable conditions for quantitative analyses at nanoscale included in the supplementary material of this manuscript.

Highlights.

• We presented the off-axis electron holography calibration in dual-lens mode of a JEOL ARM 200F.

• We provide optimal conditions for a wide field of views varying the objective lens excitation.

• The calibration was made using Au-nanoparticles controlling fringe width,spacing and contrast.

• Application of electron holography to nanoparticles is also shown.