Manifold Diffusion for Exophytic Kidney Lesion Detection on Non-Contrast CT Images

Abstract

Kidney lesions are important extracolonic findings at computed tomographic colonography (CTC). However, kidney lesion detection on non-contrast CTC images poses significant challenges due to low image contrast with surrounding tissues. In this paper, we treat the kidney surface as manifolds in Riemannian space and present an intrinsic manifold diffusion approach to identify lesion-caused protrusion while simultaneously removing geometrical noise on the manifolds. Exophytic lesions (those that deform the kidney surface) are detected by searching for surface points with local maximum diffusion response and using the normalized cut algorithm to extract them. Moreover, multi-scale diffusion response is a discriminative feature descriptor for the subsequent classification to reduce false positives. We validated the proposed method and compared it with a baseline method using shape index on CTC datasets from 49 patients. Free-response receiver operating characteristic analysis showed that at 7 false positives, the proposed method achieved 87% sensitivity while the baseline method achieved only 22% sensitivity. The proposed method showed far fewer false positives compared with the baseline method which makes it feasible for clinical practice.

1 Introduction

Extracolonic findings on CT colonography (CTC) increase the chance of early detection of high-risk lesions with economic benefits[12]. Kidney lesions are one important extracolonic finding, belonging to C-RADS E2-E4 types[18]. Existing kidney lesion detection methods[9] take advantage of contrast in the intensity values of lesions on contrast-enhanced CT images. For CTC, however, intravenous contrast material is not given since it is not necessary for colonic polyp detection. On non-contrast CTC images, the intensity values of kidneys, lesions, and adjacent organs are similar as shown in Fig. 1a. Lack of texture cues makes the task of kidney lesion detection substantially challenging in the image domain.

Fig. 1.

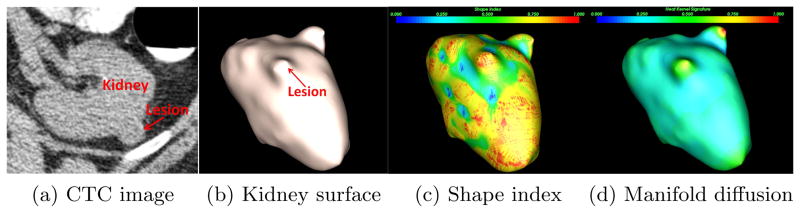
Kidney lesion detection on the non-contrast CT. (a) An exophytic lesion is located in the left kidney. (b) The lesion presents as a protuberance on the kidney surface. (c) Shape index fails to identify the lesion because it is noisily distributed on the kidney surface. Blue to red represents small to large values. (d) Manifold diffusion can accurately identify shape changes at the lesion location.

Exophytic kidney lesions are located at kidney edges, and they appear as protuberances on the kidney surface in Fig. 1b. We thus resort to shape analysis approaches to identify lesion-caused protuberances. Shape index[6] is a single-value measurement of local surface topology according to the principal curvature and widely applied to tumor detection in colon[17], breast[5], and bladder[8]. Fig. 1c shows the shape index distribution over the kidney model of Fig. 1b. Despite the fact that shape index values are large at lesion regions and small at flat or concave areas, almost all protrusion surfaces are in red in Fig. 1c, partly due to noise, which introduces many false positives. Geometric noises can be smoothed based on local curvatures[4]. However, over-smoothing easily causes lesion protuberances to vanish. To compensate for this issue, the heat kernel diffusion[14] is often used to extract global shape spectrums by treating models as manifolds in Riemanian space. Semantic geometry features are preserved by choosing small spectrums. Due to this beneficial property, Lai et al.[7] applied this approach to extract geometric features to perform supine and prone colon registration. Unfortunately, the high complexity of heat kernel smoothing makes it difficult to create simple feature descriptors for kidney lesion detection.

In this paper, we present a manifold diffusion method to create a compact, multi-scale heat kernel feature for detection and classification of exophytic kidney lesions. Fig. 1d illustrates our manifold diffusion response among the kidney surface. Note that the kidney lesion is located at the region with local maximum response (yellow) in comparison to its neighborhoods (green). In addition, diffusion response varies smoothly over the kidney surface, which is a desirable property to reduce false positives. Our kidney lesion detection framework is built on this diffusion process. Lesion candidates are extracted by the normalized cut algorithm on the vertex-weighted graph with the diffusion response as the weight. The multi-scale diffusion response is also discriminative to classify kidney lesions and reduce false positives. We validated our detection algorithm on CTC datasets from 49 patients and free response receiver operating characteristic analysis showed that the proposed method significantly outperformed shape index approach with high detection accuracy and low false positive rate.

2 Methodology

Kidneys are segmented from CTC image using our earlier work[10]. The marching cubes algorithm[11] is then applied to extract the kidney surface, which usually contains 35000–45000 vertices.

2.1 Manifold Diffusion

The kidney surface can be treated as a three-dimensional complete Riemannian sub-manifold M of ℝ³. A diffusion process on M is governed by the heat equation,

$$\left(\frac{\partial }{\partial t}+{\mathit{\Delta }}_M\right)u(x,t)=0$$ (1)

where Δ_M is the Laplace-Beltrami operator[16]. If M has boundaries and f(0, x) = δ_x : M → ℝ denotes an initial heat distribution on M, the solution u(x, t) is called the heat distribution at a point x at time t and lim_t→0 u(x, t) = f. Here, δ_x is the Dirac delta function. For any M, there exists a function k_t(x, y) : ℝ⁺ × ℝ³ × ℝ³ → ℝ, which leads to

$$u(x,t)={\int }_M{k}_t(x,y)f(y)dy$$ (2)

k_t(x, y) is called the heat kernel and measures the amounts of the heat transferred from x to y at time t. According to graph spectral theory[3], k_t(x, y) can be decomposed as

$$k_t(x,y)=\sum _{i\ge 0}{e}^{-{\lambda }_{i}t}{\varphi }_i(x){\varphi }_i(y)$$ (3)

Here, λ_i and ϕ_i are, respectively, the i^th eigenvalue and the i^th eigenfunction of the Laplace-Beltrami operator. The parameter t takes the scale role in the shape analysis as adjusting it can produce a family of k_t(x, y). However, local geometrical descriptor using k_t(x, y) is very complex because it involves both spatial and temporal variables. Instead, in this work, we set x = y and create a compact manifold diffusion process by collecting a set of auto-diffusivity functions {k_t(x, x)}_t>0, where k_t(x, x) means the remaining heat at a point x after time t. Fig. 2 illustrates our manifold diffusion response at different temporal scales. Fine scale response is maximized at the location of the small lesion protrusion (A) in Fig. 2a. The kidney surface with local maximum scale response is gradually shifted to large protrusions at lesions (B) and (C) in Fig. 2a, and eventually stops at two kidney tips because they are the most stable protrusions shown in Fig. 2d. Therefore, our manifold diffusion process at small temporal scales is a good fit for kidney lesion detection.

Fig. 2.

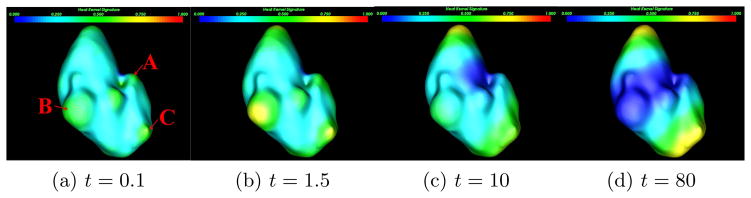
Manifold diffusion response at different temporal scales. Here, three kidney lesions marked as A, B, and C are used to illustrate multi-scale diffusion response on their detection.

Manifold diffusion response is also useful to create semantic shape descriptors for kidney lesion classification. First, the Laplace-Beltrami operator is intrinsically defined on the manifold M, and our feature descriptor established on this operator for lesion classification is thus invariant under isometric transformation. In other words, our feature descriptor is insensitive to the variability among kidney lesions. Second, it is a compact shape descriptor that can densely measure shape variance on the kidney surface. Third, the feature descriptor is very informative, as it keeps all information about the intrinsic geometry of the manifold[16]. Lastly, in contrast to conventional surface smoothing algorithms[4] that cause lesions to fade, the feature descriptor from manifold diffusion is built on the kidney surfaces with original resolutions.

2.2 Kidney Lesion Detection and Classification

After manifold diffusion is established, we exploit scale response to assign the vertex weight of the kidney surface graph. Because kidney lesions are highlighted at small temporal scales in Fig. 2, we choose a sequence of fine scale responses to allow for our framework to identify lesions with different sizes. In our implementation, we choose t ∈ {0.1, 0.3, 0.5, 0.8, 1.0, 1.2, 1.5} in Eq. 3. The kidney graph is then partitioned to search for sub-graphs with local maximum scale response, as kidney lesions typically stay in these regions. Fig. ?? summarizes the process of our kidney lesion detection, which consists of four main steps.

Step 1: Seed point determination

This step aims to find a sequence of vertices with local maximum diffusion response at each temporal scale level to facilitate graph partitioning. A seed point v_s is determined if it fulfills k_t(v_s, v_s) = arg max_v∈ring₍₃₎(k_t(v, v)), where ring means the neighbors of v on the graph[4]. The detected seed points are illustrated as green points in Fig. 3a.

Fig. 3.

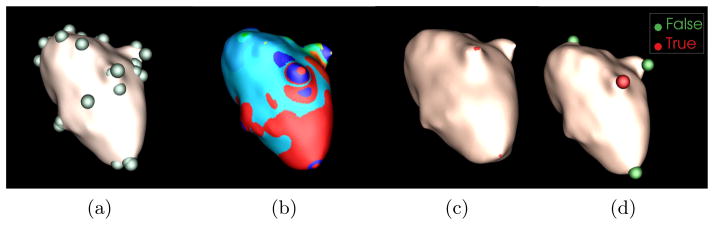
Process of kidney lesion detection contains four main steps. (a) Seed point determination, (b) graph partition, (c) kidney lesion candidate selection, and (d) lesion detection and classification.

Step 2: Graph partitioning

Because the kidney surface is represented as a graph, the normalized cut algorithm[15] is used to partition it. Let G = (E, V) be the graph with the edge set E and the vertex set V. The edge weight is assigned with the sum of scale response difference across a sequence of temporal scales.

$$d(v_1,v_2)={\left({\int }_{0.1}^{1.5}{(k_t(v_1,v_1)-k_t(v_2,v_2))}^2\right)}^{1/2},(v_1,v_2)\in E$$ (4)

A cut is to find a set of edges cut(A, B) = Σ_{v1∈A,v2∈B} d(v₁, v₂) to separate G into two disjoint sets A and B with similar scale response values. Normalized cut is computed as

$$\mathit{Ncut}=\frac{\mathit{cut}(A,B)}{\mathit{assoc}(A,V)}+\frac{\mathit{cut}(A,B)}{\mathit{assoc}(B,V)}$$ (5)

where assoc(A, V) = Σ_{v1∈A,v2∈V} d(v₁, v₂) and assoc(B, V) is similarly defined. Normalized cut is iteratively performed until no graph partitions contain two seed points. Fig. 3b shows the partition results where each sub-graph is represented as a color band.

Step 3: Candidate selection

A partition is regarded as a lesion candidate if its scale response is the local maximum and its area is less than a experimentally determined threshold, α = 400mm², because the partition includes parts of the lesion surface and the size of a lesion is limited. Fig. 3c illustrates the lesion candidates in red regions.

Step 4: Lesion detection and classification

We mapped the center point of the lesion candidates to the original CT image. A 10 × 10 × 10 sub-image centered at the mapped point is constructed for computing appearance features. Mean and standard deviation of intensity values as well as speeded up robust feature (SURF) descriptor[1] are used to describe the lesion appearance. Multi-scale manifold diffusion response is used to characterize lesion shape. We combine appearance and shape information to formulate the final feature vector and train the support vector machine classifier[2] using Gaussian radial basis function as the kernel. The final detection is shown in Fig. 3d. Here, red spheres represent true detections and green ones false positives.

2.3 Validation Datasets and Methods

The framework for kidney lesion detection was validated on non-contrast CTC images from 49 patients. The slice thickness was 1mm. 25 patients have at least one kidney lesion, and the total number of lesions is 50. 46 of them are situated on the kidney surface. All lesions are marked by an experienced radiologist as the groundtruth. 19 lesions are located in the left kidney, and the remaining 31 are in the right kidney. Their size range is 3.2–40.5mm. Retrospective analyses of these images were approved by our Office of Human Subjects Research. To better understand our approach, shape index is chosen as the baseline method for its popularity in tumor detection[5, 17, 8]. We follow the same detection strategy described above to find lesion candidates at graph regions with shape index value larger than 0.9.

3 Experimental Results

Our training dataset contains 15 patients and the testing set 34 patients. There were 14 true kidney lesions in the training set and 36 true kidney lesions in the test set. For the proposed method, there were 18 true detections (TP) (from 13 unique kidney lesions) and 128 false positives (FP) in the training set; 33 TP (31 unique) and 277 FP in the test set. For the baseline method based on shape index, there were 16 TP (7 unique) and 354 FP in the training set; 76 TP (18 unique) and 1080 FP in the test set. The proposed method generated 8 false positives per patient and the shape index generated 32 false positives per patient. Shape index also missed many lesions because the areas of their graph partitions are large than α at step 3 in the section 2.2.

In Fig. 4, we show the free-response receiver operating characteristic (FROC) curves on the test set with and without anatomical guidance. Fig. 4 shows that at 7 FPs, the sensitivity of the proposed method is 87% and the baseline method based on shape index is only 22%. These promising results demonstrated that our algorithm can accurately detect kidney lesions from non-contrast CTC images. Note that there were five true kidney lesions missed by the proposed method due to their locations (inside the kidney, not on the surface).

Fig. 4.

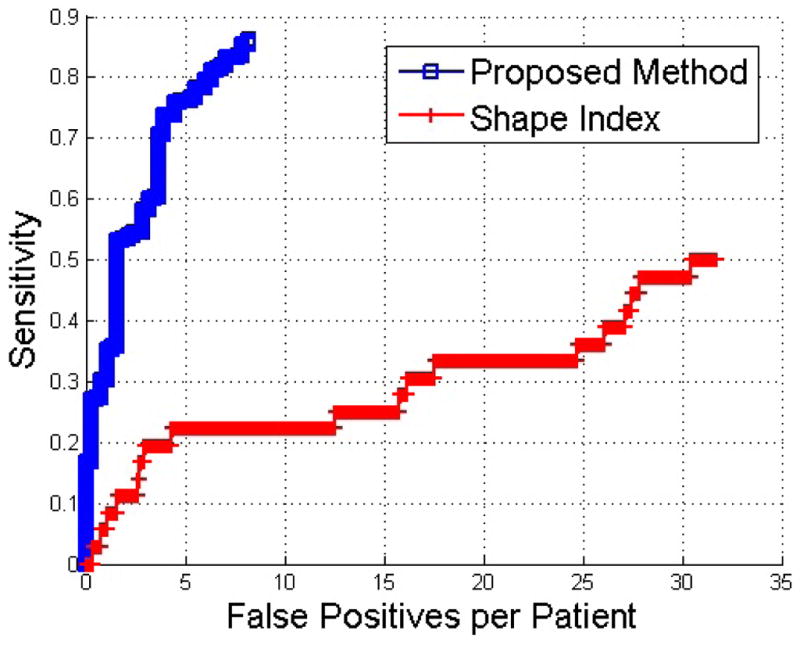
Comparison of FROC curves of the proposed method and the baseline detection method based on shape index.

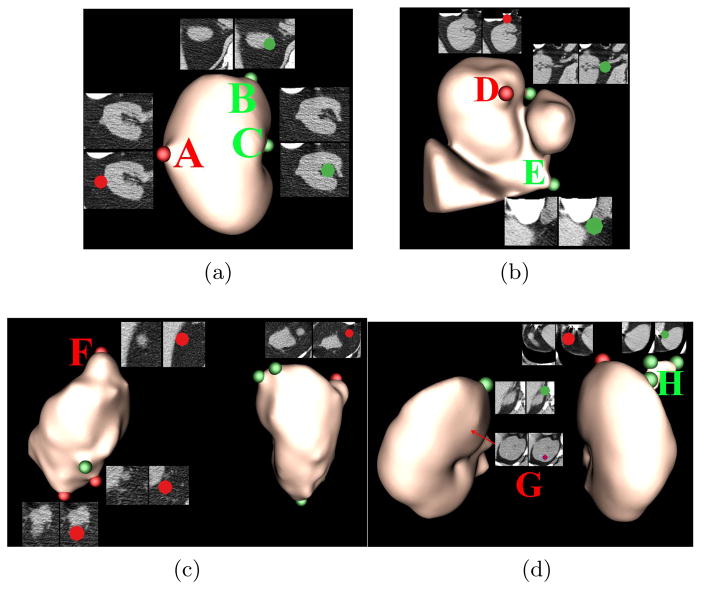
Fig. 5 illustrates kidney lesion detection on images of four patients with kidney lesions. In Fig. 5a, a kidney lesion was located in the left kidney. Our detection strategy identified it with two FPs. FP (B) stayed at the tip of kidney, similar to the lesion (F) in Fig. 5c. FP (C) was close to the renal vein, which was one of the main sources of false positives. Fig. 5b shows a challenging case as the left kidney was improperly segmented. However, our algorithm can still find lesion (D) with only two FPs. FP (E) was caused by the incorrect kidney segmentation. The patient in Fig. 5c has four lesions. Three of them were located in the left kidney, and the remaining one in the right kidney. Our detection algorithm accurately found all of them. There were two lesions in Fig. 5d. Our algorithm detected the one on the right kidney surface, while missed the Lesion (G) indicated by the red arrow internal to the left kidney because of no shape variance on the kidney surface. There were several FPs caused by the renal vein, such as (H). Nevertheless, experimental results demonstrated that our detection algorithm can accurately identify exophytic kidney lesions with a few FPs due to the renal vein, inaccurate kidney segmentation, and kidney tips.

Fig. 5.

Exophytic kidney lesion detection on four patient images. True detections are labeled in red and false detections in green. Sub-images are also extracted from the original CT to illustrate the detection. In Fig. 5b, inaccurate kidney segmentation contains part of liver (triangular object), and the inferior vena cava (round blob).

4 Conclusion and Future Work

In this work, we developed a novel manifold diffusion method and showed its application to detect exophytic kidney lesions. It treated kidney surfaces as manifolds in the Riemannian space and generated a heat diffusion process on the manifolds by only considering temporal scale changes. Therefore, our manifold diffusion was a compact process, which can assist in kidney lesion detection and classification. The experiments demonstrated that our algorithm outperformed shape index with high detection accuracy and low false positive rate.

In the future, we will be investigating the renal vein atlas to reduce false positives as well as identifying texture and shape characteristics of internal kidney lesions. We are also developing an automatic scale selection metric for manifold diffusion instead of fixing a set of scales. Moreover, we are comparing our method with other shape descriptors, such as shape-DNA[13] and heat kernel smoothing[14].