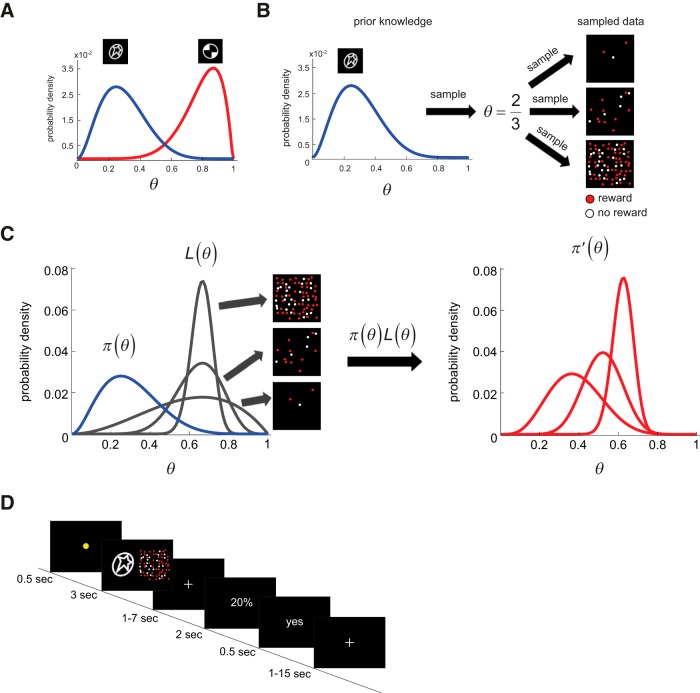
Figure 1.

Overview of Bayesian integration and experimental design. A, Prior distributions. Two probability density functions on a parameter θ that takes on the value between 0 and 1. In this study, θ was the reward probability associated with a lottery option, termed the “symbol lottery.” There were two density functions, each represented by a white-on-black icon shown above the peak of each distribution. These density functions served as prior distributions on θ. Subjects had to first learn each density function in the behavioral session (Session 1). B, Generating current sensory information (likelihood). In the integration task (Session 2), on each trial, a sample was drawn from the prior distribution corresponding to the icon displayed to determine the reward probability of the symbol lottery (θ). In this example, we assume that θ = 2/3 for convenience but, of course, it may take on any value between 0 and 1. The subjects did not know this value and had to estimate it. One source of information was the prior experience s/he had with the icon in the previous behavioral session. The other source was current sensory information about the true value of θ, which was generated by sampling with replacement based on θ. The sample was presented as randomly distributed dots (red and white dots that indicated reward and no reward respectively). There were three possible sample sizes (three dots, 15 dots, 75 dots) implemented in this study. C, Bayesian integration of prior and likelihood information. To optimally combine prior and likelihood information, an ideal Bayesian decision maker multiplies the prior distribution, π(θ), which represents prior beliefs, and the likelihood function, L(θ), which represents current sensory information about θ, resulting in the posterior distribution π′(θ). D, Trial sequence in the fMRI session (Session 2). Information about the symbol lottery was presented for 3 s and was followed by a variable 1–7 s interstimulus interval. After the interstimulus interval, the choice screen appeared. Information about the reward probability associated with the alternative lottery was revealed explicitly in numeric form and subjects had up to 2 s to make a choice between the symbol lottery and the alternative lottery with a button press.