Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2016 Jan 31.
Published in final edited form as: Neuroimage. 2014 Nov 26;106:154–160. doi: 10.1016/j.neuroimage.2014.11.040

Does Degree of Gyrification Underlie the Phenotypic and Genetic Associations between Cortical Surface Area and Cognitive Ability?

Anna R Docherty a,*, Donald J Hagler Jr b, Matthew S Panizzon c,d, Michael C Neale a, Lisa T Eyler c,f, Christine Fennema-Notestine c,b, Carol E Franz c,d, Amy Jak c,g, Michael J Lyons h, Daniel A Rinker c,b, Wesley K Thompson c, Ming T Tsuang c,d,g,i, Anders M Dale c,b,j, William S Kremen c,d,g
PMCID: PMC4313767  NIHMSID: NIHMS649293  PMID: 25433211

Abstract

The phenotypic and genetic relationship between global cortical size and general cognitive ability (GCA) appears to be driven by surface area (SA) and not cortical thickness (CT). Gyrification (cortical folding) is an important property of the cortex that helps to increase SA within a finite space, and may also improve connectivity by reducing distance between regions. Hence, gyrification may be what underlies the SA-GCA relationship. In previous phenotypic studies, a 3-dimensional gyrification index (3DGI) has been positively associated with cognitive ability and negatively associated with mild cognitive impairment, Alzheimer’s disease, and psychiatric disorders affecting cognition. However, the differential genetic associations of 3DGI and SA with GCA are still unclear. We examined the heritability of 3DGI, and the phenotypic, genetic, and environmental associations of 3DGI with SA and GCA in a large sample of adult male twins (N = 512). Nearly 85% of the variance in 3DGI was due to genes, and 3DGI had a strong phenotypic and genetic association with SA. Both 3DGI and total SA had positive phenotypic correlations with GCA. However, the SA-GCA correlation remained significant after controlling for 3DGI, but not the other way around. There was also significant genetic covariance between SA and GCA, but not between 3DGI and GCA. Thus, despite the phenotypic and genetic associations between 3DGI and SA, our results do not support the hypothesis that gyrification underlies the association between SA and GCA.

Keywords: gyrification, cortical folding, cognitive ability, heritability, twin, aging

1. Introduction

The formation of cortical folding is highly reproducible within species, with minor individual variations (Rakic, 2009). Yet the purposes of cortical folding across the lifespan are still unknown. The degree of gyrification of the human brain has historically been believed to reflect a need to increase SA without disproportionately increasing head size (e.g., Armstrong et al., 1995; Reillo et al., 2011). Various theories have been posited to explain patterns of cortical folding. It may, for example, be a way of improving connectivity by reducing distance between regions (for a review of gyrification and connectivity, see Zilles et al., 2013) or the reduction of axonal length between cortical areas (Van Essen, 1997; for a review see White & Hilgetag, 2011). It also seems likely that improved connectivity provides a means of allowing for increased cognitive capacity. Primate research seems consistent with this hypothesis. For example, studies of primates have indicated that larger brains have increased folding relative to smaller brains (e.g., Rilling & Insel, 1999), and among more recently evolved primates, convolution has been found to have increased at a faster pace than has brain size (Zilles, 1989). Consequently, degree of gyrification might reflect cognitive changes most distinctive to human primates, and may modulate intelligence in humans.

Folding, and consequent surface expansion of the cerebral cortex, appears to be an important factor in influencing mammalian cognitive abilities (for a review, see Sun & Hevner, 2014). Overall, there are converging lines of evidence consistent with differential expansion being a mechanism for gyrification; the idea of connectivity as the primary function of gyrification has generally not been supported (Sun & Hevner, 2014; Ronan et al.,2014; for studies modeling increased cortical thickness without gyrification, see Murre & Sturdy, 1995 and Ruppin et al, 1993). Of the small number of gyrification studies published to date, the phenotype has been studied largely in relation to neuropsychiatric disorders such as Alzheimer’s disease, autism, velocardial facial syndrome, and schizophrenia (Liu et al., 2012; Wallace et al., 2013; Schaer et al., 2013; Kates et al., 2009; Schaer et al., 2006; Palaniyappan et al., 2012; Nanda et al., 2013). Wallace et al. (2013) reported that while autism-spectrum cases did not differ from controls in SA, they exhibited significant posterior gyrification increases bilaterally. This group made the case that lack of gyrification-SA association may reflect developmentally dissociable phenotypes, and that gyrification increases could lead to certain cognitive abilities observed in people with autism-spectrum disorders. Gyrification has also been negatively associated with psychosis and 22q11 deletion syndrome (e.g., Palaniyappan et al., 2012; Nanda et al., 2013; Schaer et al., 2006), both genetic conditions notable for multiple cognitive deficits (reviews by Elvevag & Goldberg, 2000; Green et al., 2004; Eisenberg et al., 2010). An examination of Alzheimer’s disease cases found that global gyrification and sulcal width differentiated mild Alzheimer’s cases from healthy controls (Liu et al., 2012). Mild cognitive impairment has also been associated with greater than normal reductions in gyrification in late-life (Liu et al., 2013). The latter findings suggest that gyrification might be very relevant to cognitive aging.

Other research has examined the relevance of gyrification to normative aging. A study by Zilles et al. (1988) manually measured 3DGI postmortem in the brains of 61 adults ages 16– 91. This early study of a gyrification index, similar to the index derived currently using our MRI methods, manually measured degree of gyrification using multiple histological brain slices. Manual measurement of postmortem brain is very labor-intensive, and in that study it required the measurement of only every fourth slice of the brain. They found no significant relationship between 3DGI and age. Using different types of measures, Magnotta et al. (1999) observed reduced gyrification with age in the brains of 148 adults aged 18–82 years based on measures of sulcal and gyral curvature. Hogstrom and colleagues (2013) reported results from an MRI study of 322 adults ages 20–85, and found that 3DGI decreased with age (Hogstrom et al., 2013). This study used the same index of gyrification as in the present study, one that is based on the entire cortex.

Some research suggests that genetic factors have a strong influence on sulci and gyri during neurodevelopment (Piao et al., 2004). Evaluating gyral patterns in monozygotic (MZ) twins, Lohmann et al. (1999) observed that deeper and developmentally earlier sulci of the brain are more highly correlated between twins than are the surface sulci. They concluded that more superficial sulci, developing after birth, may be more affected by environmental influences.

These two early studies are limited by the fact that they each included only about 20 twin pairs. These are considered to be very small sample sizes for twin analysis, something that may substantially increase the risk of unreliable results (Neale & Cardon, 1992; Martin et al., 1978). In addition, Lohman et al. (1999) included only MZ twins. Without including dizygotic (DZ) twins, analyses cannot fully disentangle genetic influences from those due to the common environment (Neale & Cardon, 1992). The development of semi-automated techniques has made it possible for subsequent MRI twin studies to have substantially larger sample sizes. That, in turn, has made it possible to obtain more reliable estimates of the amount of variance in gyrification that is accounted for by genetic and environmental influences.

It is important to note, in addition, that our index of gyrification is different from the gyrification that has been examined in these twin studies. They were examining gyral patterns. In the present study, we examined degree of gyrification. The difference is analogous to shape versus volume of brain structures. Gyral patterns reflect the extent to which the patterns (or exact locations) are the same. We are measuring degree of gyrification such that one can have the same amount of gyrification without the gyri and sulci being in the same location. Heritability of the former is likely to be lower than heritability of the latter; it is probable that gyral patterns are less heritable than degree of gyrification.

In 515 middle-aged twins in the Vietnam Era Twin Study of Aging (VETSA; Kremen et al., 2006, 2013), we previously examined the genetic covariance among total SA, mean CT, and GCA (Vuoksimaa et al., 2014). SA, rather than CT, drove the phenotypic and genetic associations between cortex and GCA. As noted, previous research suggests that gyrification is positively phenotypically associated with cognitive ability and negatively phenotypically associated with Alzheimer’s disease and mild cognitive impairment. These findings raise the possibility that gyrification could be the underlying source of our observed SA-GCA relationships. We are unaware of any genetically informative studies of degree of gyrification or of the relationship between gyrification and cognitive ability. The goals of the present study were to: 1) estimate the heritability of gyrification; 2) examine the phenotypic and genetic associations between gyrification and SA, given that gyrification is related to SA; and 3) test whether gyrification underlies the relationship between SA and GCA.

2. Materials and Methods

2.1 Participants

Brain imaging and cognitive data at age 51–60 years were obtained for men enrolled in the Vietnam Era Twin Study of Aging (VETSA; Kremen et al., 2006, 2013). The VETSA sample is representative of community-dwelling U.S. men within their age range based on sociodemographic and health characteristics (Kremen et al., 2006, 2013; Schoeneborn and Heyman, 2009). All participants had been in prior military service at some time between 1965 and 1975, and most (~80%) had not been exposed to combat. In other words, these were Vietnam era, not necessarily Vietnam war, veterans. Of 534 who were scanned, 512 had analyzable 3DGI data: 132 MZ twin pairs, 92 DZ twin pairs, and 64 unpaired twins. Participants chose a study site at either the University of California San Diego or Boston University. If they chose to do the study at Boston University, participants were brought to Massachusetts General Hospital for scanning procedures. All participants gave written informed consent to participate. The Institutional Review Board at each participating institution approved the study protocol.

Representativeness of the VETSA sample has been reported in detail elsewhere (Kremen et al., 2006; 2013). Overall, the prevalence for health conditions is consistent with population data for American men in this age range as reported from the 2004–2007 National Health Interview Survey by the Centers for Disease Control and Prevention (Schoeneborn & Heyman, 2009). In this sample, years of education M(SD) = 13.8 (2.1), body mass index M(SD) = 28.8 (4.2), the Center for Epidemiological Studies of Depression Scale (CES-D; Radloff, 1977) current depression M(SD) = 8.2 (8.1), median = 6.0. In this sample, 24% were current smokers, 9% had diabetes, and 59% had hypertension. As cited previously, the VETSA MRI sample did not differ from the rest of the VETSA sample on any of these variables (Panizzon et al., 2008). The VETSA sample is also comparable to the general population in this age range with respect to AFQT score variance. The average AFQT score for this sample is equivalent to an IQ score of 104–5 (Kremen et al., 2011). Variances of brain measures in this sample are similar to other samples in the literature, including samples in other twin studies. Socio-economic status in this sample was normally distributed and heterogeneous, with the broadest range of scores possible (M = 5.5, SD = 1.8, sample range = 0–9). Demographic and psychiatric information is presented in Table 1.

Table 1.

Demographic Characteristics & Prevalence of Psychiatric Disorders (N = 512)

Mean Age (SD) 56.14(2.63)
Ethnicity (%)
  Latino/a 3
  Asian 0
  Native American/Islander <1
  African American 5
  White 88
Lifetime Diagnosis (%)
  Depressive Disorder 15
  Anxiety Disorder 6
  PTSD 5
  Alcohol or Drug Abuse/Dependency 2
  Schizophrenia <1
Open in a new tab

Note: SD = standard deviation. PTSD = Posttraumatic stress disorder.

2.2 GCA measure

GCA was measured with the Armed Forces Qualification Test (AFQT). This test is a 50-minute paper-and-pencil test that correlates highly (r = .84) with the Wechsler Adult Intelligence Scale IQ score (Lyons et al., 2009; McGrevy et al., 1974), and has strong test-retest reliability of .74 over 35 years (Lyons et al., 2009). The AFQT includes components assessing verbal ability (synonyms), visual-spatial processing (mentally folding and unfolding boxes), arithmetic, and reasoning about tools and mechanical relations. In this sample, the Armed Forces Qualification Test mean score was 63 (SD = 21), which corresponds to an IQ of 104–105.

2.3 Image acquisition and processing

A more detailed description of the MRI image acquisition and processing can be found in Kremen et al. (2010) and Eyler et al. (2012). Images were acquired on Siemens 1.5 Tesla scanners. Two sagittal T1-weighted MPRAGE sequences were employed with a TI=1000ms, TE=3.31ms, TR=2730ms, flip angle=7 degrees, slice thickness=1.33mm, voxel size 1.3×1.0×1.3mm. To increase signal-to-noise ratio, the MPRAGE acquisitions were rigid-body registered for motion correction and then averaged. The 3-dimensional cortical surface was reconstructed to measure thickness and areal expansion at each surface location (over 300,000 locations in total bilaterally). This was done using a semi-automated approach in the FreeSurfer software package (Dale and Sereno, 1993; Dale et al., 1999; Fischl et al., 1999). Continuous maps of the cortex were obtained by means of vertices in a standardized, spherical atlas space surface tessellation. This method provides estimates of the relative areal expansion and compression of each vertex in atlas space, in addition to vertex-wise estimates of thickness. Estimates of CT were based on the shortest distances between the gray-white boundary and the pial surface (Dale & Sereno, 1993; Dale et al., 1999; Fischl et al., 1999). Total SA was calculated as a sum of SA of all cortical vertices (excluding mid-brain vertices) (Eyler et al., 2012). 3DGI was calculated as the ratio between the total area of the pial surface -- excluding non-cortical vertices and summed across hemispheres -- and the summed area of outer brain surfaces for each hemisphere. Outer brain surfaces were created to enclose a filled mask generated from the pial surface, as described by Schaer et al. (Schaer et al. 2008, 2012). This method of calculating 3DGI provies a global measure of gyrification, but is similar in principle to the local gyrification index used by Hogstrom et al. (2013).

2.4 Statistical analysis

In order to determine the relative influence of genetic and environmental factors on 3DGI, we fit a trivariate (SA, 3DGI, GCA) model to the data. In the classical twin design, the variance of each phenotype is decomposed into the proportion of total variance attributed to additive genetic (A) influences, common or shared environmental (C) influences, and unique environmental (E) influences (Eaves et al., 1978; Neale and Cardon, 1992). The name ‘ACE model’ is derived from these three components of variance. Additive genetic influences are assumed to correlate 1.0 between MZ twins who generally share 100% of their genes, and .5 between DZ twins who on average share 50% of their segregating genes. Shared environment is assumed to correlate 1.0 between both members of a twin pair, regardless of twin zygosity. Unique environmental influences are assumed to be uncorrelated between the members of a twin pair. Measurement error is also included in the E term because it is also assumed to be uncorrelated between twins.

The proportion of a phenotype’s total variance attributable to additive genetic influences is considered the heritability of the phenotype. The significance of genetic or shared environmental influences was tested by fixing the parameter in question to zero, and then comparing the fit of the reduced model against the full model. No such test was performed for the unique environmental influences because this parameter must always be present in the model. No covariates were entered into the analyses. Model comparisons were performed using the likelihood-ratio chi-square test (LRT), calculated as the difference in the −2 log likelihood (−2LL) of the reduced model from that of the full model. Significant LRT values (p < .05) indicate a significant change in model fit relative to the comparison model.

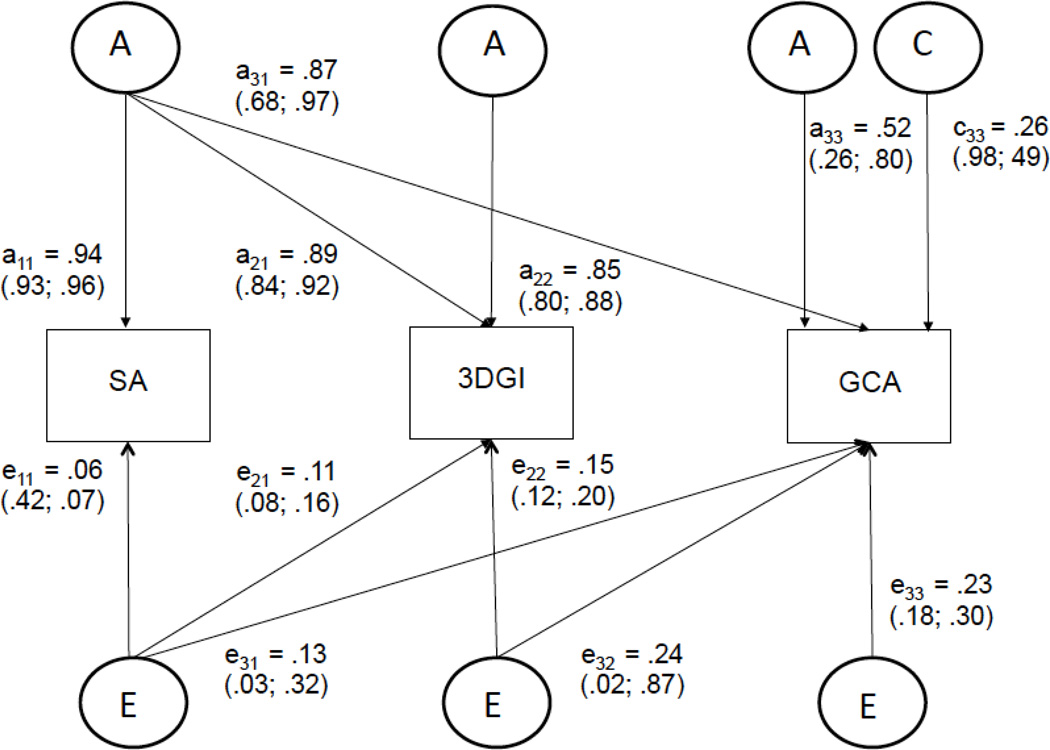
We also examined whether phenotypes share common genetic and environmental determinants with 3DGI. We examined genetic covariance and environmental covariance of 3DGI with SA and with GCA. As can be seen in Figure 1, a Cholesky model decomposes the total covariance between phenotypes into genetic (A) and environmental components (C and E) such that the summed standardized genetic and environmental covariances are equal to the phenotypic correlation.

Figure 1.

Figure 1

Open in a new tab

A path diagram depicting a trivariate Cholesky decomposition. Within twin pairs, covariance shared by the three phenotypes (shown in boxes) is generated by latent additive genetic (A), shared environmental (C), and unique environmental (E) components (shown in circles). The genetic correlation is the standardized genetic covariance (e.g., a11*a21 / √(a112 * (a212+a222)) (A), while the unique environmental correlation is the proportion of variance shared due to unique (unshared) environmental causes (e.g., e11*e21 / √(e112 * (e212+e222)) (E). All latent variables A have fixed variances of 1.0 (not shown). Presented here is the best fitting trivariate model of SA, 3DGI, and GCA. Numbers reflect the standardized estimates within the best fitting model along with 95% confidence intervals. This figure corresponds to model 4 in Table 3, in which the shared additive genetic variance between 3DGI and GCA is held to zero. Hence, there is no a32 path. There are also no C components for SA or 3DGI in this model because they were also set to zero in this best fitting model. For simplification of presentation, the model shows only one twin.

Genetic and environmental covariance estimates can also be used to derive the genetic and environmental correlations between the phenotypes. A genetic correlation (rg) is defined as the proportion of variance that two traits share due to genetic causes (A), while environmental correlation (rc or re) is the proportion of variance shared due to common (C) or unique environmental causes (E). A phenotypic correlation is defined as the total proportion of all genetic and environmental variance shared by two traits. Because genetic and environmental correlations can have opposing signs resulting in phenotypic correlations that are near zero, analyses were run regardless of the observed phenotypic correlation between the measures.

Because gyrification is a property of SA, the two are likely to be strongly related to one another. Therefore, it was essential to include both phenotypes in the same model. In a trivariate Cholesky model, the first factor influences all three variables of interest (Figure 1), while the second factor influences only the second and the third, and the third factor influences only the third variable. The models included SA, 3DGI, and GCA, in that order. Models were systematically tested to examine the worsening of the model fit caused by the removal of the various sources of variation; for example, examining the fit of the full model versus a model in which the genetic path between 3DGI and GCA is set to zero. This comparison tests whether removing the genetic path between 3DGI and GCA significantly diminishes the model fit or whether the 3DGI-GCA path is not important to the overall prediction of genetic variance in GCA. We additionally tested a nested model in which genetic path SA-GCA was set to zero. This comparison was to examine whether 3DGI contributes any genetic variance in GCA beyond what SA contributes to GCA.

The Akaike Information Criterion (AIC) provides an index of model fit based on the -2LL, in which the lowest and most negative value corresponds to the most parsimonious model. So in addition to examining the change in fit between models, we examined the AIC to determine which model was most parsimonious.

All analyses were performed using maximum-likelihood-based modeling software OpenMx (Boker et al., 2011). Structural brain measures were adjusted for the effects of age and scanner prior to the model fitting process. Adjustments for scanner are critical to account for the influence of hardware differences on structural measures (Han et al., 2006).

3. Results and Discussion

All of the results presented are based on the trivariate genetic analyses because they provide more precise estimates than univariate analyses.

3.1 Genetic and environmental influences on the brain measures

Variance components from the full trivariate model are presented in Table 2, indicating a significant proportion of variance in each phenotype attributable to genetic factors. Within the full trivariate analysis of SA, 3DGI, and GCA, heritability of 3DGI was 0.71 (95%CI 0.62; 0.79). Influences of shared environment were nonexistent at 0.0 (95%CI 0.00; 0.38).

Table 2.

Tests of Genetic and Shared Environmental Variance from the Full Trivariate Model

Variance components (95% CI)
a2 c2 e2
SA 0.98 (0.86;1.00) 0.08 (0.00;0.48) 0.24 (0.21;0.27)
3DGI 0.71 (0.62;0.79) 0.00 (0.00;0.38) 0.27 (0.24;0.30)
GCA 0.68 (0.45;0.87) 0.00 (0.00;0.68) 0.47 (0.41;0.53)
Open in a new tab

Note: a2 = additive genetic variance, c2 = shared environmental variance, e2 = unique, unshared environmental variance, SA = cortical surface area, 3DGI = local gyrification index, GCA = general cognitive ability.

Values in bold reflect statistical significance, while italicized values are not significant.

All statistics are based on the full trivariate model of SA, 3DGI, and GCA.

3.2. Phenotypic and genetic associations among the brain measures

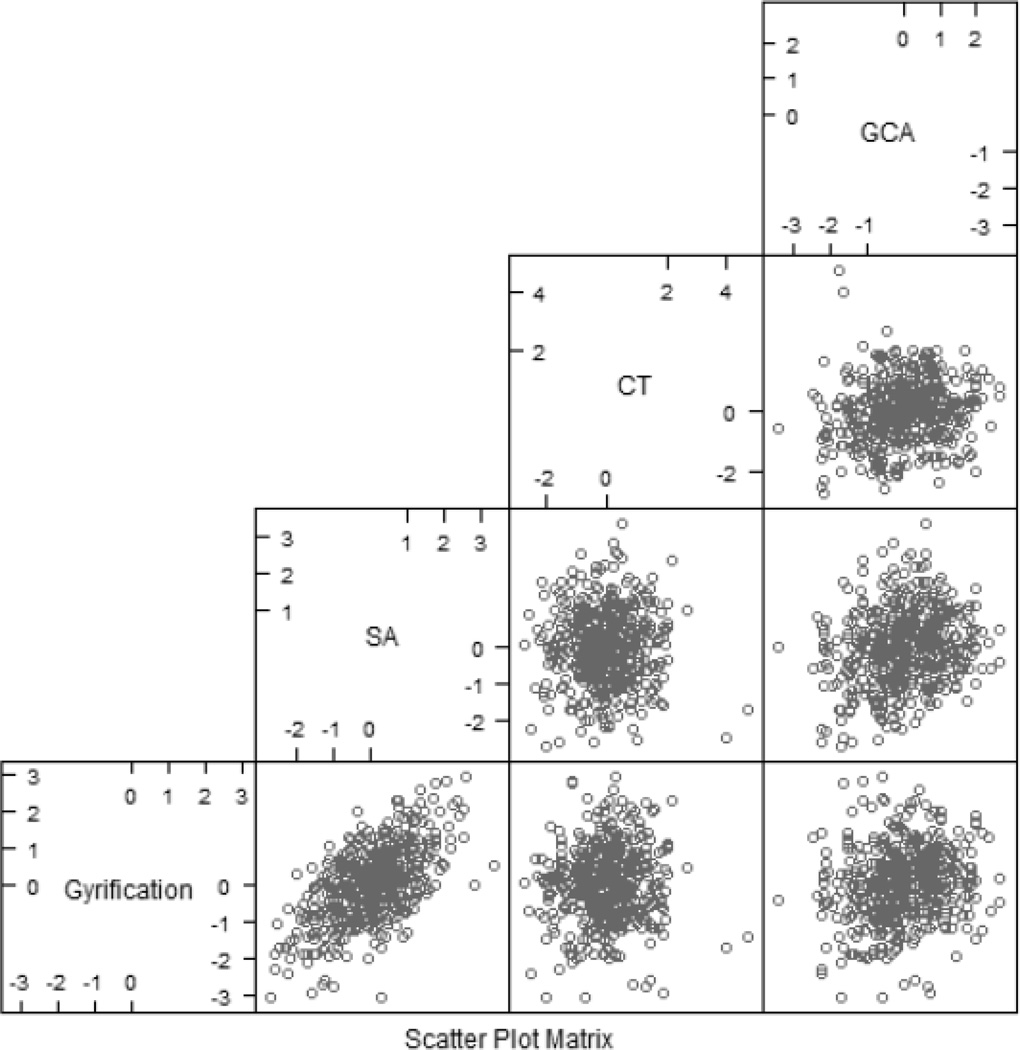
A scatterplot matrix of 3DGI, SA, CT, and GCA is presented in Figure 2.

Figure 2.

Figure 2

Open in a new tab

Scatterplot matrix showing values of gyrification, SA, CT, and GCA plotted against one another. All variables have been z-scored and adjusted for age and scanner. Along the bottom row are plots of gyrification with SA, CT, and GCA. The row above depicts plots of SA against CT and GCA. Finally, the topmost graph depicts CT plotted against GCA.

The 3DGI-SA phenotypic correlation was significant at 0.59 (95%CI 0.53; 0.65). The strong positive phenotypic correlation between 3DGI and SA was driven by shared genetic (rg = 0.56; [95%CI 0.46; 0.68]) as well as unshared environmental covariance (re = 0.29; [95%CI 0.23; 0.35]). We did not estimate common environmental correlations because the C estimates were zero for SA and 3DGI.

Because 3DGI is a property of SA and it was highly correlated with SA, we expected that like SA, 3DGI would not be related to cortical thickness. 3DGI and CT were not significantly correlated (rp = 0.04 [95%CI −0.05; 0.13]). CT was not examined further due to its lack of associations with 3DGI.

3.3. Phenotypic and genetic associations with cognitive ability

There was a significant positive phenotypic correlation between 3DGI and GCA (rp = 0.17 [95% CI 0.09; 0.26]) and a significant positive phenotypic correlation between SA and GCA (rp = 0.20 [95% CI 0.12; 0.29]). Given that 3DGI and SA were significantly phenotypically correlated with GCA and with each other, we estimated partial correlations to assess whether the phenotypic 3DGI-GCA correlation remained significant when accounting for SA, and whether the phenotypic SA-GCA correlation was reduced when accounting for 3DGI. The partial phenotypic correlation between 3DGI and GCA controlling for SA decreased the phenotypic correlation between 3DGI and GCA to 0.07 (p = ns). A partial correlation between SA and GCA after accounting for 3DGI decreased to 0.13 (p < .005). Thus, the latter correlation, between SA and GCA, remained significant even when accounting for 3DGI.

Table 3 presents the additive genetic, common environmental, and unique environmental correlations of GCA with both SA and 3DGI (these are presented on the upper diagonals shaded in grey). Standardized model estimates for each of the A, C, and E variance components are also presented in Table 2 as the unshaded values, on and below the diagonals, along with corresponding 95% confidence intervals.

Table 3.

Standardized Variance-Covariance Estimates (on and below Diagonal) and Correlations (above Diagonal in grey)
SA 3DGI GCA
Genetic
(A)		 SA .94
(.72; .96)		 .90
(.68; .99)		 1.0
(.12; 1.0)
3DGI .90
(.68; .99)		 .83
(.68; .88)		 .35
(−1.0; 1.0)
GCA 1.0
(.11; >1.0)		 .35
(−1.0; >1.0)		 .51
(.24; .78)
SA 3DGI GCA
Common
Environmental
(C)		 SA .01
(.00; .22)		 −.02
(−1.0; .21)		 −.20
(−1.0; .73)
3DGI −.02
(−.10; .21)		 −.02
(.10; .21)		 .41
(−.72; 1.0)
GCA −.20
(−1.0; .73)		 .02
(.00; .17)		 .41
(.00; >1.0)
SA 3DGI GCA
Unique
Environmental
(E)		 SA .06
(.04; .07)		 .11
(.07; .16)		 .13
(.03; .35)
3DGI .11
(.08; .16)		 .16
(.12; .21)		 .24
(.03; .79)
GCA .13
(.02; .34)		 .24
(.03; .79)		 .23
(.02; .30
Trivariate Model Comparisons
AIC −2LL DF Δ-2LL ΔDF P
1. Full Trivariate Model 383.08 3341.08 1479
2. AE-AE-ACE 374.76 3342.76 1484 1.68 5 0.892
3. SA-GCA = 0 383.91 3353.91 1485 11.15 1 <0.001
4. 3DGI-GCA = 0 372.88 3342.88 1485 0.11 1 0.73
Open in a new tab

Note: Three matrices divided by A, C, and E variance components. Values on and below the diagonals are variance and covariance estimates, in standardized form. Above the diagonals, shaded grey items reflect genetic and environmental correlations derived from the A, C, and E covariance matrices. The 95% confidence intervals are shown in parentheses; estimates are significant when the intervals do not include zero.

SA = cortical surface area, 3DGI = gyrification index, GCA = general cognitive ability.

Note: AIC = Akaike’s information criterion; −2LL = Negative 2 log-likelihood; DF = Degrees of freedom; Δ-2LL = Change in negative 2 log-likelihood; ΔDF = Change in degrees of freedom;

Model 1 reflects a full trivariate model in which A, C, and E are estimated for each of the three phenotypes.

Model 2 reflects a model in which A and E components are estimated for all variables, and C is estimated only for GCA (a slight improvement in fit). Models 3 and 4 reflect variations of model 2, in which the genetic correlation (path a) between SA or 3DGI and GCA is set to 0. Model comparison statistics reflect the fit of model 2 compared to model 1, and submodels 3 and 4 tested against of model 2. Model 4 (the best fitting model based on AIC) is also depicted in Figure 1.

3.4 Trivariate Model Comparisons

Trivariate models of SA, 3DGI, and GCA indicated that SA, but not 3DGI, accounted for a significant proportion of genetic variance in GCA. Table 3 presents statistics for the trivariate model comparisons. Model 1 in Table 3 was a full trivariate model examining A, C, and E components of each of the three phenotypes—SA, 3DGI, and GCA. Because there was virtually no shared environmental (C) variance in the two brain measures, as can be seen in Table 2, the full model was compared to a model in which the shared environmental variance components were removed from SA and 3DGI, but not removed from GCA (Model #2 in Table 3). Model 2 was compared with the full model. This model retained a good fit to the data.

Next, we fit a similar model to Model 2 in which one of the paths, the additive genetic path from SA to GCA, was held to zero (Model 3). Model 3 resulted in a significantly worse model fit compared to either of the prior two models. Finally, we fit a model in which the additive genetic path from 3DGI to GCA was held to zero (Model 4). Model 4 was also compared to Model 2. Model 4 did not reflect a significant reduction in fit to the data based on the change in - 2LL, and it also had the lowest AIC value. Therefore, we considered Model 4 to be the best fitting model, suggesting that 3DGI did not account for much of the shared genetic covariance between SA and GCA.

A diagram of the best fitting model (Model 4) is depicted in Figure 1. Here the A path (the genetic variance) from 3DGI to GCA is removed.

3.5 Summary

In a sample large enough to produce reliable heritability estimates, we showed that the degree of gyrification across the cortex as measured by the 3DGI is highly heritable. We are unaware of any previous reports of the heritability of degree of gyrification. Some prior reports based on small samples have suggested that the heritability of gyrification is somewhat lower than that of other brain structure measures, but those studies examined indices of gyrification pattern similarity, which one would expect to be less heritable than overall degree of gyrification.

We also found that there were relatively strong phenotypic and genetic associations between SA and 3DGI. These findings were expected given that 3DGI is, in part, a surface area measure. Nevertheless, the correlations of about .6 also indicate substantial phenotypic and genetic variance that is unique to each. In addition, the fact that evolutionarily there is a strong relationship between increased gyrification and increased cognitive capacity raised the possibility that the SA-GCA association that we previously reported might be driven primarily by gyrification. Although 3DGI was correlated with GCA almost as strongly as SA, partialling out the variance in SA resulted in a nonsignificant 3DGI-GCA correlation. In contrast, the SA-GCA correlation remained significant after partialling out 3DGI. Our results also suggested that genetic substrates of GCA vary as a function of genetic changes in SA, but less so as a function of genetic changes in 3DGI. Therefore, the idea that the SA-GCA correlation is mostly a function of 3DGI was not supported in the present study.

There have been few published studies examining a three-dimensional gyrification index in relation to cognitive ability in healthy individuals. The results of this study are consistent with research by Hogstrom et al suggesting a positive relationship between 3DGI and SA but a negative relationship of both with CT (Hogstrom et al., 2012). It is possible that stretching, or increase in SA at the expense of CT, is one way in which gyrification takes place over time. Future collection of gyrification data over multiple timepoints will be informative.

The debate about a possible association of gyrification with cortical thickness is still unresolved. Recently our group found research has suggested that genetic variance in GCA is more closely associated with SA than CT (Vuoksimaa et al., 2014). Previous research on CT and GCA is mixed, with approximately half of studies reporting positive results and half reporting negative results. Inconsistencies across these studies, moreover, do not appear to be associated with the age of the samples. Overall, fewer studies of SA and GCA exist than of CT and GCA, but SA studies have been more consistently positive (Vuoksimaa et al., 2014).

Some limitations should be noted with regard to this study. First, the current study used a global index of gyrification. Thus, with this measure it is not possible to ascertain whether gyrification within some predefined regions of interest are more relevant to GCA than others. Future studies using a local gyrification index (Schaer et al. 2008, 2012) or other measures such as sulcal depth may be able to address the issue of localizing areas of greater or lesser association between gyrification and cognition. Second, only male twins participated in this study, precluding any examination of sex differences. It is a strength, however, that the VETSA sample is an age-homogenous and a national, rather than a local, sample.

It is important to note that gyrification might be related to age. Although the recent reviews of twin structure do not suggest striking differences in heritability of cortical structures, it is possible that genetic and environmental variance differ at different stages of development. Middle-age is a time at which neurodegenerative processes become increasingly detectable, and so the estimated genetic factors may include those associated with cerebral health. Thus, we do not know if these results will generalize to other age groups. At almost any age some change is observed to be occurring, but heritability estimates in our sample are comparable to those of other age groups. Reviews of twin studies of brain structure have not found consistent differences in heritability estimates for young and middle-aged adults (Blokland et al., 2012). In a 5-year follow up of the VETSA sample we did not observe changes, though we will need additional longitudinal data to determine if genetic and environmental variance differentially affect degree of neurodegeneration. Both 3DGI and SA have been reported to decrease with age in a cross-sectional study (Hogstrom et al., 2012). Whether the phenotypic or genetic SA-GCA or 3DGI-GCA associations change in later life is a question that can be addressed in planned follow-up assessments.

In conclusion, we found that degree of gyrification was highly heritable, and both cortical SA and degree of gyrification were associated with GCA in midlife adults. The fact that degree of gyrification—which is a property of SA—may be associated with improved cortical connectivity, and that across species gyrification is associated with cognitive capacity led us to examine whether gyrification might be what was driving the phenotypic and genetic associations between SA and GCA. However, our findings did not support the notion that gyrification was the underlying reason that cortical SA was associated with GCA.

Acknowledgements

This work was supported by NIA grants R01 AG022381, AG018386, and AG022982 to WSK, and R01 AG018384 to MJL, and Academy of Finland grant 257075 to EV. This material was, in part, the result of work supported with resources of the VA San Diego Center of Excellence for Stress and Mental Health Healthcare System. The content is solely the responsibility of the authors and does not necessarily represent official views of the NIA, NIH, or VA. The Cooperative Studies Program of the U.S. Department of Veterans Affairs provided financial support for development and maintenance of the Vietnam Era Twin Registry. Numerous organizations provided invaluable assistance in the conduct of this study, including: Department of Defense; National Personnel Records Center, National Archives and Records Administration; the Internal Revenue Service; National Opinion Research Center; National Research Council, National Academy of Sciences; the Institute for Survey Research, Temple University. The authors gratefully acknowledge the continued cooperation and participation of the members of the VET Registry and their families, and the time and energy of many staff and students on the VETSA projects.

Glossary

AFQT

Armed Forces Qualification Test

CT

cortical thickness

GCA

general cognitive ability

GI

gyrification index

3DGI

3-dimensional gyrification index

SA

surface area

VETSA

Vietnam Era Twin Study of Aging

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Conflict of interest

Anders M. Dale is a founder and holds equity in CorTechs Laboratories, Inc., and also serves on its Scientific Advisory Board. The terms of this arrangement have been reviewed and approved by the University of California, San Diego, in accordance with its conflict of interest policies. All other authors report no potential conflicts of interest.

References

  1. Armstrong E, Schliecher A, Omran H, Curtis M, Zilles K. The ontogeny of human gyrification. Cerebral Cortex. 1995;5(1):56–63. doi: 10.1093/cercor/5.1.56. [DOI] [PubMed] [Google Scholar]
  2. Boker S, Neale M, Maes H, Wilde M, Spiegel M, Brick T, Fox J. OpenMx: An Open Source Extended Structural Equation Modeling Framework. Psychometrika. 2011;76(2):306–317. doi: 10.1007/s11336-010-9200-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Caviness VS., Jr Mechanical model of brain convolutional development. Science. 1975;189(4196):18–21. doi: 10.1126/science.1135626. [DOI] [PubMed] [Google Scholar]
  4. Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis. I. Segmentation and surface reconstruction. NeuroImage. 1999;9(2):179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
  5. Dale AM, Sereno MI. Improved Localizadon of Cortical Activity by Combining EEG and MEG with MRI Cortical Surface Reconstruction: A Linear Approach. J Cogn Neurosci. 1993;5(2):162–176. doi: 10.1162/jocn.1993.5.2.162. [DOI] [PubMed] [Google Scholar]
  6. Dominicus A, Skrondal A, Gjessing HK, Pedersen NL, Palmgren J. Likelihood ratio tests in behavioral genetics: problems and solutions. Behav Genet. 2006;36(2):331–340. doi: 10.1007/s10519-005-9034-7. [DOI] [PubMed] [Google Scholar]
  7. Eaves LJ, Last KA, Young PA, Martin NG. Model-fitting approaches to the analysis of human behaviour. Heredity (Edinb) 1978;41(3):249–320. doi: 10.1038/hdy.1978.101. [DOI] [PubMed] [Google Scholar]
  8. Eisen S, True W, Goldberg J, Henderson W, Robinette CD. The Vietnam Era Twin (VET) Registry: method of construction. Acta Genet Med Gemellol (Roma) 1987;36(1):61–66. doi: 10.1017/s0001566000004591. [DOI] [PubMed] [Google Scholar]
  9. Eisenberg DP, Jabbi M, Berman KF. Bridging the gene-behavior divide through neuroimaging deletion syndromes: Velocardiofacial (22q11.2 Deletion) and Williiams (7q11.23 Deletion) syndromes. NeuroImage. 2010;53(3):857–869. doi: 10.1016/j.neuroimage.2010.02.070. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Elvevag B, Goldberg TE. Cognitive impairment in schizophrenia is the core of the disorder. Crit Rev Neurobiol. 2000;14(1):1–21. [PubMed] [Google Scholar]
  11. Eyler LT, Chen CH, Panizzon MS, Fennema-Notestine C, Neale MC, Jak A, Kremen WS. A comparison of heritability maps of cortical surface area and thickness and the influence of adjustment for whole brain measures: a magnetic resonance imaging twin study. Twin Res Hum Genet. 2012;15(3):304–314. doi: 10.1017/thg.2012.3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Fischl B, Sereno MI, Dale AM. Cortical surface-based analysis. II: Inflation, flattening, and a surface-based coordinate system. Neuroimage. 1999;9(2):195–207. doi: 10.1006/nimg.1998.0396. [DOI] [PubMed] [Google Scholar]
  13. Green MF, Nuechterlein KH, Gold JM, Barch DM, Cohen J, Essok S, Marder SR. Approaching a consensus cognitive battery for clinical trials in schizophrenia: the NIMH-MATRICS conference to select cognitive domains and test criteria. Biol Psychiatry. 2004;56(5):301–307. doi: 10.1016/j.biopsych.2004.06.023. [DOI] [PubMed] [Google Scholar]
  14. Han X, Jovicich J, Salat D, van der Kouwe A, Quinn B, Czanner S, Fischl B. Reliability of MRI-derived measurements of human cerebral cortical thickness: the effects of field strength, scanner upgrade and manufacturer. NeuroImage. 2006;32(1):180–194. doi: 10.1016/j.neuroimage.2006.02.051. [DOI] [PubMed] [Google Scholar]
  15. Henderson WG, Eisen S, Goldberg J, True WR, Barnes JE, Vitek ME. The Vietnam Era Twin Registry: a resource for medical research. Public Health Rep. 1990;105(4):368–373. [PMC free article] [PubMed] [Google Scholar]
  16. Hogstrom LJ, Westlye LT, Walhovd KB, Fjell AM. The structure of the cerebral cortex across adult life: age-related patterns of surface area, thickness, and gyrification. Cereb Cortex. 2013;23(11):2521–2530. doi: 10.1093/cercor/bhs231. [DOI] [PubMed] [Google Scholar]
  17. Hogstrom LJ, Westlye LT, Walhovd KB, Fjell AM. The structure of the cerebral cortex across adult life: age-related patterns of surface area, thickness, and gyrification. Cereb Cortex. 2013;23(11):2521–2530. doi: 10.1093/cercor/bhs231. [DOI] [PubMed] [Google Scholar]
  18. Kremen WS, Thompson-Brenner H, Leung YM, Grant MD, Franz CE, Eisen SA, Lyons MJ. Genes, environment, and time: the Vietnam Era Twin Study of Aging (VETSA) Twin Res Hum Genet. 2006;9(6):1009–1022. doi: 10.1375/183242706779462750. [DOI] [PubMed] [Google Scholar]
  19. Kremen WS, Prom-Wormley E, Panizzon MS, Eyler LT, Fischl B, Neale MC, Fennema-Notestine C. Genetic and environmental influences on the size of specific brain regions in midlife: the VETSA MRI study. NeuroImage. 2010;49(2):1213–1223. doi: 10.1016/j.neuroimage.2009.09.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Kremen WS, Panizzon MS, Xian H, Barch DM, Franz CE, Grant MD, Toomey R, Lyons MJ. Genetic architecture of context processing in late middle age: More than one underlying mechanism. Psychology and Aging. 2011;26:852–863. doi: 10.1037/a0025098. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Liu T, Lipnicki DM, Zhu W, Tao D, Zhang C, Cui Y, Jin JS, Sachdev PS, Wen W. Cortical gyrification and sulcal spans in early stage Alzheimer's disease. PLoS One. 2012;7(2) doi: 10.1371/journal.pone.0031083. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Liu T, Sachdev PD, Lipnicki D, Jiang J, Cui Y, Kochan NA, Wen W. Longitudinal changes in sulcal morphology associated with late-life aging and MCI. NeuroImage. 2013;74:337–342. doi: 10.1016/j.neuroimage.2013.02.047. [DOI] [PubMed] [Google Scholar]
  23. Lohmann G, von Cramon DY, Steinmetz H. Sulcal variability of twins. Cereb Cortex. 1999;9(7):754–763. doi: 10.1093/cercor/9.7.754. [DOI] [PubMed] [Google Scholar]
  24. Lyons MJ, York TP, Franz CE, Grant MD, Eaves LJ, Jacobson KC, et al. Genes determine stability and the environment determines change in cognitive ability during 35 years of adulthood. Psychological Science. 2009;20(9):1146–1152. doi: 10.1111/j.1467-9280.2009.02425.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Magnotta VA, Andreasen NC, Schultz SK, Harris G, Cizadlo T, Heckel D, Flaum M. Quantitative in vivo measurement of gyrification in the human brain: changes associated with aging. Cereb Cortex. 1999;9(2):151–160. doi: 10.1093/cercor/9.2.151. [DOI] [PubMed] [Google Scholar]
  26. Martin NG, Eaves LJ, Kearsey MJ, Davies P. The power of the classical twin study. Heredity (Edinb) 1978;40(1):97–116. doi: 10.1038/hdy.1978.10. [DOI] [PubMed] [Google Scholar]
  27. McGrevy DF, Knouse SB, Thompson RA. Relationships among an individual intelligence test and two air force screening and selection tests. San Antonio, TX: Personnel Research Division, Air Force Human Resources Laboratory, Brooks Air Force Base; 1974. Technical Report AFHRL-TR-74-25. [Google Scholar]
  28. Murre JM, Sturdy DP. The connectivity of the brain: multi-level quantitative analysis. Biol Cybern. 1995;73(6):529–545. doi: 10.1007/BF00199545. [DOI] [PubMed] [Google Scholar]
  29. Nanda P, Tandon N, Mathew IT, Giakoumatos CI, Abhishekh HA, Clementz BA, Keshavan MS. Local Gyrification Index in Probands with Psychotic Disorders and Their First-Degree Relatives. Biol Psychiatry. 2013 doi: 10.1016/j.biopsych.2013.11.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Neale MC, Cardon LR. Methodology for genetic studies of twins and families. Dordrecht, The Netherlands: Kluwer Academic Publishers; 1992. [Google Scholar]
  31. Palaniyappan L, Liddle PF. Aberrant cortical gyrification in schizophrenia: a surface-based morphometry study. J Psychiatry Neurosci. 2012;37(6):399–406. doi: 10.1503/jpn.110119. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Piao X, Hill RS, Bodell A, Chang BS, Basel-Vanagaite L, Straussberg R, Dobyns WB, Walsh CA. G protein-coupled receptor-dependent development of human frontal cortex. Science. 2004;303(5666):2033–2036. doi: 10.1126/science.1092780. [DOI] [PubMed] [Google Scholar]
  33. Radloff LS. The CES-D scale: A self-report depression scale for research in the general population. Appl. Psychol. Meas. 1977;1:385–401. [Google Scholar]
  34. Rakic P. Evolution of the neocortex: a perspective from developmental biology. Nat Rev Neurosci. 2009;10(10):724–735. doi: 10.1038/nrn2719. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Reillo I, de Juan Romero C, Garcia-Cabezas MA, Borrell V. A role for intermediate radial glia in the tangential expansion of the mammalian cerebral cortex. Cereb Cortex. 2011;21(7):1674–1694. doi: 10.1093/cercor/bhq238. [DOI] [PubMed] [Google Scholar]
  36. Rilling JK, Insel TR. The primate neocortex in comparative perspective using magnetic resonance imaging. J of Human Evolution. 1999;37(2):191–223. doi: 10.1006/jhev.1999.0313. [DOI] [PubMed] [Google Scholar]
  37. Ronan L, Voets N, Rua C, Alexander-Bloch A, Hough M, Mackay C, Fletcher PC. Differential tangential expansion as a mechanism for cortical gyrification. Cereb Cortex. 2014;24:2219–2228. doi: 10.1093/cercor/bht082. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Ruppin E, Schwartz EL, Yeshurun Y. Examining the volume efficiency of the cortical architecture in a multi-processor network model. Biol Cybern. 1993;70(1):89–94. doi: 10.1007/BF00202570. [DOI] [PubMed] [Google Scholar]
  39. Schaer M, Schmitt JE, Glaser B, Lazeyras F, Delavelle J, Eliez S. Abnormal patterns of cortical gyrification in velo-cardio-facial syndrome (deletion 22q11.2): an MRI study. Psychiatry Res. 2006;146(1):1–11. doi: 10.1016/j.pscychresns.2005.10.002. [DOI] [PubMed] [Google Scholar]
  40. Schaer M, Cuadra MB, Tamarit L, Lazeyras F, Eliez S, Thiran JP. A surface-based approach to quantify local cortical gyrification. IEEE Trans Med Imaging. 2008;27(2):161–170. doi: 10.1109/TMI.2007.903576. [DOI] [PubMed] [Google Scholar]
  41. Schaer M, Cuadra MB, Schmansky N, Fischl B, Thiran JP, Eliez S. How to measure cortical folding from MR images: a step-by-step tutorial to compute local gyrification index. J Vis Exp. 2012;59:e3417. doi: 10.3791/3417. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Schoeneborn CA, Heyman KM. National Health Statistics Reports. Vol. 16. Hyattsville, MD: National Center for Health Statistics; 2009. Health characteristics of adults aged 55 years and over: United States, 2004–2007. [PubMed] [Google Scholar]
  43. Self SG, Liang KY. Large sample properties of the maximum likelihood estimator and the likelihood ratio test on the boundary of the parameter space. Journal of the American Statistical Association. 1987;82:605–611. [Google Scholar]
  44. Steiger JH, Shapiro A, Browne MW. On the multivariate asymptotic distribution of sequential chi-square statistics. Psychometrika. 1985;50(3):253–264. [Google Scholar]
  45. Sun T, Hevner RF. Growth and Folding of the mammalian cerebral cortex: from molecules to malformations. Nat Rev Neurosci. 2014;15(4):217–232. doi: 10.1038/nrn3707. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Van Essen DC. A tension-based theory of morphogenesis and compact wiring in the central nervous system. Nature. 1997;385(6614):313–318. doi: 10.1038/385313a0. [DOI] [PubMed] [Google Scholar]
  47. Vuoksimaa E, Panizzon MS, Chen CH, Fiecas M, Eyler LT, Fennema-Notestine C, et al. The genetic association between neocortical volume and general cognitive ability is driven by surface area rather than thickness. Cerebral Cortex. 2014 doi: 10.1093/cercor/bhu018. Epub ahead of print. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Wallace GL, Robustelli B, Dankner N, Kenworthy L, Giedd JN, Martin A. Increased gyrification, but comparable surface area in adolescents with autism spectrum disorders. Brain. 2013;136(6):1956–1967. doi: 10.1093/brain/awt106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Wu H, Neale MC. Adjusted confidence intervals for a bounded parameter. Behav Genet. 2012;42(6):886–898. doi: 10.1007/s10519-012-9560-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Wu H, Neale MC. On the likelihood ratio tests in bivariate acde models. Psychometrika. 2013;78(3):441–463. doi: 10.1007/s11336-012-9304-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Zilles K, Armstrong E, Schleicher A, Kretschmann HJ. The human pattern of gyrification in the cerebral cortex. Anat Embryol (Berl) 1988;179(2):173–179. doi: 10.1007/BF00304699. [DOI] [PubMed] [Google Scholar]
  52. Zilles K, Palomero-Gallagher N, Amunts K. Development of cortical folding during evolution and ontogeny. Trends Neurosci. 2013;36(5):275–284. doi: 10.1016/j.tins.2013.01.006. [DOI] [PubMed] [Google Scholar]

RESOURCES