Fig. 2.
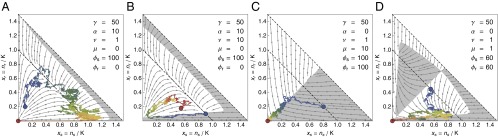
Control of a tumor cell population. (A–D) The optimal control profile under perfect information about and for different parameters of the cancer model. In the white areas, (no drug), whereas in the gray areas, (with drug). The arrows indicate the deterministic flow. All profiles were calculated via Eq. 9 with generations and with an absorbing boundary at . The sample trajectories were simulated with and controlled according to these profiles. The coloring of the trajectories shows the temporal evolution from blue to red. (A) When selection against resistance is stronger than driver emergence, , the optimal protocol is to wait until resistant cells are cleared from the system before the drug is applied. (B) For higher driver emergence rates, the drug is applied earlier, which can lead to cycles. (C) For drug-sensitive and drug-addicted cells with high mutation , the control in the symmetric case is a simple majority rule and very effective. (D) For smaller mutation , the optimal strategy first homogenizes the tumor before trying to remove it.
