A model for time to fracture with a shock stream superimposed on progressive degradation: the Study of Osteoporotic Fractures

Abstract

Osteoporotic hip fractures in the elderly are associated with a high mortality in the first year following fracture and a high incidence of disability among survivors. We study first and second fractures of elderly women using data from the Study of Osteoporotic Fractures (SOF). We present a new conceptual framework, stochastic model and statistical methodology for time to fracture. Our approach gives additional insights into the patterns for first and second fractures and the concomitant risk factors. Our modeling perspective involves a novel time-to-event methodology called threshold regression which is based on the plausible idea that many events occur when an underlying process describing the health or condition of a person or system encounters a critical boundary or threshold for the first time. In the parlance of stochastic processes, this time to event is a first hitting time of the threshold. The underlying process in our model is a composite of a chronic degradation process for skeletal health combined with a random stream of shocks from external traumas, which taken together trigger fracture events.

1. Introduction

Osteoporotic hip fractures in the elderly are associated with a high mortality in the first year following fracture and a high incidence of disability among survivors. A first hip fracture is often followed by a second hip fracture, with most of the second fractures occurring on the opposite hip to the first. Chapurlat et al. [1] used data from the Study of Osteoporotic Fractures (SOF) to investigate second fractures. Their statistical modeling and analysis made use of a stratified proportional hazards methodology to identify relevant risk factors for second fractures. We have revisited the same data set with a different conceptual framework and a new statistical model and analysis in order to gain additional insights into the patterns for first and second fractures and the concomitant risk factors. Our modeling perspective involves a novel time-to-event methodology called threshold regression which we describe in Section 3.

2. The Study of Osteoporotic Fractures

The Study of Osteoporotic Fractures (SOF) is an ongoing longitudinal study that recruited 9,704 white women, who were at least 65 years old, from community-based listings by mailings between September 1986 and October 1988 to four metropolitan clinic centers in the United States (Baltimore, Maryland; Portland, Oregon; Minneapolis, Minnesota; and the Monongahela Valley, Pennsylvania) [2]. Standardized interviews and clinical examinations were conducted approximately every two years to prospectively collect risk factors for osteoporosis. The data include anthropometric measurements, bone mineral density (BMD) measurements, cognitive and physical functions, falls, vision, lifestyle characteristics, family and medical histories, and other risk factors for osteoporotic fractures. Additionally, between 1997 and 1998, 662 African American women were recruited to this original cohort. Follow-up rates of participants exceeded 98% as efforts were made every quarter to ascertain fractures, falls or change in address by postcard or telephone. The events of interest were incident and second hip fractures. Hip fractures were confirmed by review of radiographs [2, 3].

Our analyses excluded 662 African-Americans recruited at year 10 of the SOF study because their risk of fracture is low (2.5 times lower than white women [4]) and a shorter follow-up due to late recruitment may result in a smaller number of women with incident hip fractures. Other exclusion criteria include women who were unable to walk without assistance, women with bilateral hip replacements, and women who reported hip fractures prior to enrollment.

First hip fractures

Risk factors for first hip fractures are well-characterized [5–14]. These include age, body mass index (BMI), weight change since 25 years old, parental history of fracture, previous fracture at age less than 50 years, total hip and femoral neck BMD, fall and faint histories, co-morbidities like rheumatoid arthritis, Parkinson’s disease, diabetes, stroke and hyperthyroidism, use of medications like hormone replacement therapy, long-acting benzodiazepine (sleep medication) and glucocorticoids (steroids), use of supplements such as vitamin D and calcium, and lifestyle factors such as walk for exercise, consumption of alcohol, caffeine and tobacco smoking.

Second hip fractures

Although risk factors for first hip fractures are well characterized, epidemiologic knowledge of risk factors for the prevention of a second hip fracture is lacking. Studies that have examined risks for a second hip fracture have identified old age, low bone mass, dementia, dizziness, impaired depth perception, impaired mobility, previous falls and poor self-rated health as important factors [1, 15–25].

3. The Conceptual Setting

The conceptual setting for our analysis can be sketched as follows. Each subject has a stochastic process Y (t) that describes his or her skeletal strength Y as a function of time t. Process Y (t) is an overlay and interplay of (1) a chronic degradation process D(t) representing slow and largely irreversible physiological deterioration of the skeleton and (2) a medication process M(t) representing intermittent medical treatment with diets, therapies, medications, and even lifestyle interventions. We assume that the skeletal health process is a linear combination of components D(t) and M(t), as follows:

$$Y(t)=Y(0)-D(t)+M(t)$$ (1)

Value Y (0) = y₀ is taken as the subject’s baseline skeletal strength at time t = 0. The deterioration and medication processes are assumed to start at zero at baseline (time 0), that is, D(0) = M(0) = 0. In addition to process Y (t), we postulate that the subject is exposed to an independent external stochastic process V (t) that represents a stream of random external shocks to the skeleton, of varying force, caused by accidental falls and other physical traumas experienced by the subject over time.

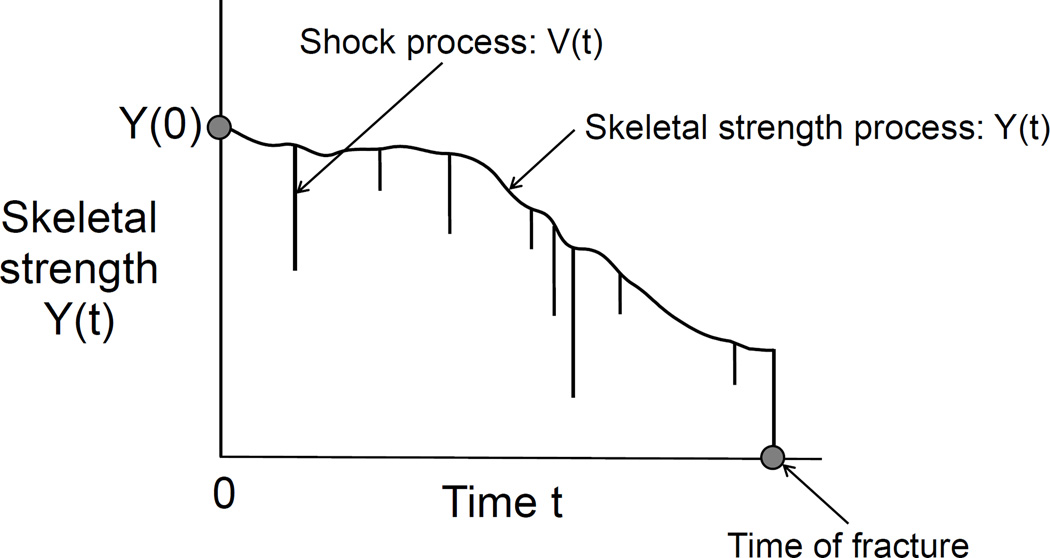
Figure 1 illustrates the imagined sample path for a typical subject. The adjective ‘imagined’ is used because the full process is unobservable, although parts of it can be intermittently inferred from data, such as the SOF data set. The sample path in this figure shows the overlay of the skeletal strength process Y (t) and the shock process V (t). The subject experiences a fracture on the first occasion after baseline when the sample path passes through the zero level. This event is marked by a dot in the figure and occurs at the first moment that a shock exceeds the patient’s skeletal strength and therefore triggers the fracture event. The figure shows why time-to-fracture, denoted later by S, involves the notion of a first hitting time (FHT) and, hence, the need for threshold regression (TR) methods. Threshold regression is based on the plausible idea that many events occur when an underlying process describing the health or condition of a person or system encounters a critical boundary or threshold for the first time. In the parlance of stochastic processes, this time to event is a first hitting time of the threshold. TR methods can take account of covariates, such as age, co-morbidities, medications, and the like, that may strongly influence the time course of the individual sample path. In TR regression, regression structures can be given to any or all parameters of the model, including the initial or starting level of the process, the stochastic process itself, the threshold or boundary, and even the time scale of the process. See Lee and Whitmore [26, 27] and Lee et al. [28] for an overview of threshold regression methodology, some applications, and a study of its connection to proportional hazards regression.

Figure 1.

A conceptual stochastic process model for skeletal strength, an external shock process and time to fracture.

4. The Model

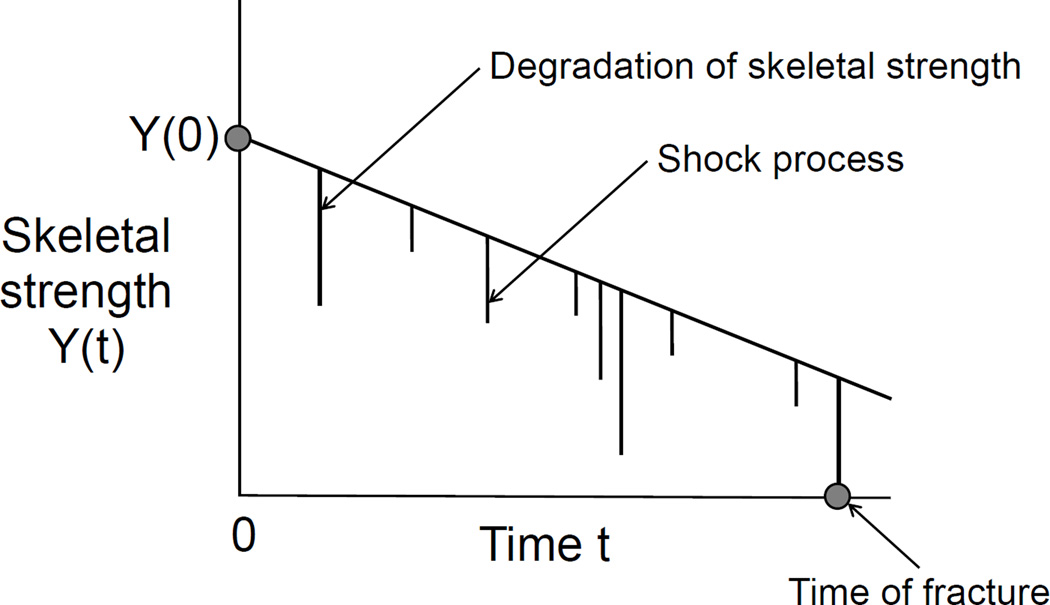
Figure 2 shows a simplified version of the full conceptual model that we will apply in this setting. In this simplified version, the intrinsic skeletal strength of an elderly subject declines steadily from its initial level Y (0). The subject then experiences a stationary random stream of shocks V (t). The first shock that arrives and exceeds the intrinsic skeletal strength produces a fracture. Statistical theory that we present shortly shows that the time to this fracture can be modeled by an exponential-like distribution that we call the TR degradation-shock model. The fracture event, of course, alters the time course of health for the subject. It may precipitate complications that cause death or, if not death, may produce a completely new health context because of medications, limited functionality, medical treatment, life style changes, etc. In this post-fracture state, the skeletal health process proceeds in an altered state. Again, the superposition of chronic degradation, medication, and shock processes produce an altered sample path for the subject. A subsequent shock may produce a second fracture. The context is dynamic and complex but a simple formulation imagines that the arrival time of the next fracture, if it is to occur, will again have this same TR degradation-shock distribution but with new parameter values.

Figure 2.

Pictorial representation of the time to skeletal fracture as a first hitting time for a composite stochastic process consisting of a stream of random shocks superimposed on a progressive degradation process for skeletal strength.

For our application here, we represent chronic degradation of the skeleton by a deterministic exponential decay path. Specifically, we assume that skeletal strength has an initial level y₀ at the outset of the study and then experiences chronic degradation over time according to an exponential trend at a constant rate λ. The mathematical function for the degradation path is

$$y(t)=y_0\text{exp}(\lambda t).$$ (2)

Skeletal strength declines if λ < 0, in which case skeletal strength y(t) approaches the zero level asymptotically. In this situation, chronic skeletal strength weakens steadily over time and approaches the fracture point but never reaches it because y(t) remains positive. A shock is required to drive skeletal strength to zero and trigger a fracture. A downward exponential degradation trend is depicted in Figure 2. The figure illustrates how a shock finally produces a fracture when the combined degradation and shock process first hits zero strength. We now outline our model.

The shock stream is taken as a stochastic process {V (t)} that consists of a dense sequence of independent draws from a common probability distribution. Specifically, the probability that all shocks in process {V (t)} which occur in time interval (t, t + dt) will be of size υ or smaller is given by G(υ)^dt. Here G(υ) denotes the cumulative distribution function for the maximum shock size experienced during any unit of time and dt is an infinitesimal positive increment. In formal notation, P[max_u∈(t,t+dt] V (u) ≤ υ] = G(υ)^dt. A hip fracture is avoided in any time interval (0, s] if no shock occurs that exceeds skeletal strength during the interval; in other words, if max_u∈(t,t+dt] V (u) ≤ y(t) for all t ∈ (0, s]. Employing the assumption of independent outcomes over all differential time increments in (0, s] and recalling that the log-probability of a joint outcome of independent events is the sum of the respective log-probabilities of the constituent events, it follows that the log-probability that no fracture will occur in interval (0, s] is given by:

$$\text{ln}\overline{F}(s)=\text{ln}P(S>s)={\int }_0^s\text{ln}G[y(t)]dt$$ (3)

This function is the log-survival time for the fracture event.

A realistic and tractable result for (3) is obtained if ln G(υ) has the following reciprocal power form:

$$\text{ln}G(\upsilon )=-{\left(\frac{\alpha }{\upsilon }\right)}^{\beta }\text{for}\alpha >0,\beta >0$$ (4)

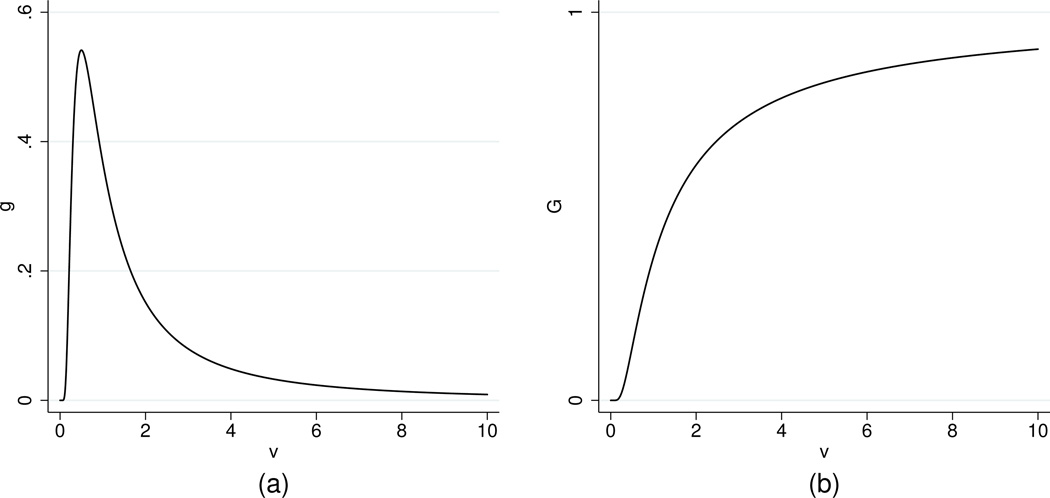
This distribution is the Fréchet extreme-value distribution, which has the general behavior that we are seeking for a shock model [29]. Figure 3 shows the probability density function g(υ) and cumulative distribution function G(υ) for a demonstration case of the shock distribution in (4).

Figure 3.

Plots of the probability density and cumulative distribution functions for the shock distribution with α = 1 and β = 1: (a) g(υ) = (1/υ²) exp(−1/υ), (b) G(υ) = exp(−1/υ).

We now present the log-survival function (3) for an exponential degradation trend, which has a simple closed mathematical form. Substituting y(t) = y₀ exp(λt) into (3) and reducing the expression gives:

$$\text{ln}\overline{F}(s)=\text{ln}P(S>s)=\frac{1}{\beta \lambda }{\left(\frac{\alpha }{y_0}\right)}^{\beta }[\text{exp}(-\beta \lambda s)-1]$$ (5)

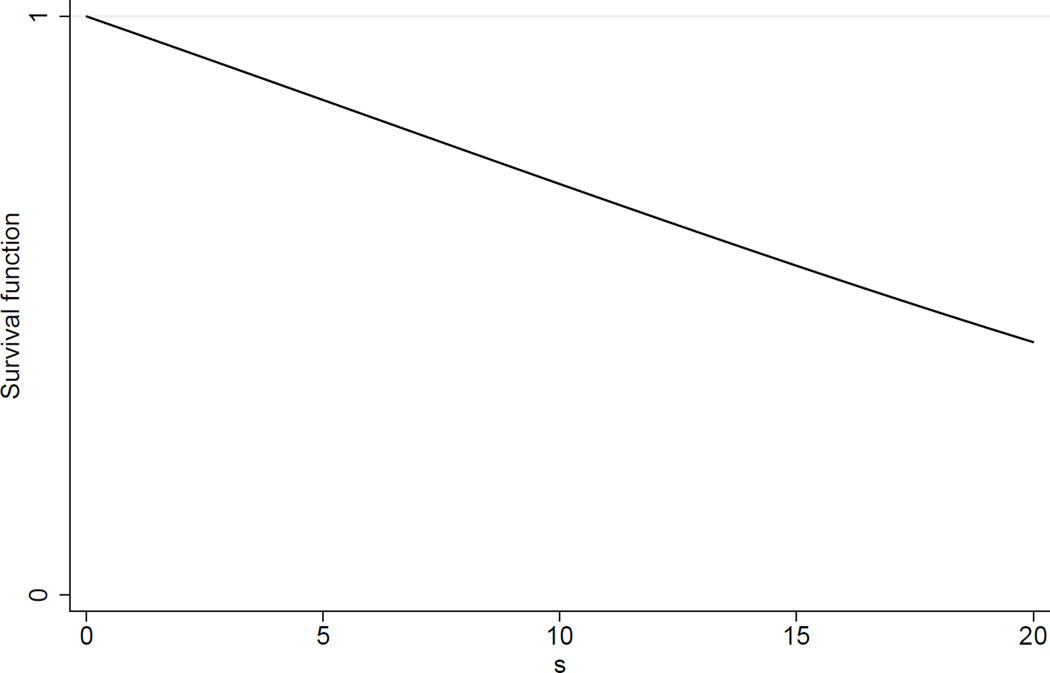
Figure 4 shows a plot of the survival function for a demonstration case of the fracture model.

Figure 4.

Plot of the survival function F̅(s) = exp[(1 − e^0.035s)/1.225], corresponding to parameter values α = 1 and β = 1 for the shock distribution and a degradation curve starting at initial strength y₀ = 35 with rate parameter λ = −0.035.

If the degradation path is rising away from the threshold at zero with λ > 0 then there is a positive probability that the subject will never have a fracture. This probability is given by

$$\text{ln}P(S=\infty )=-\frac{1}{\beta \lambda }{\left(\frac{\alpha }{y_0}\right)}^{\beta }\text{if}\lambda >0.$$ (6)

In the special case where λ = 0, there is no progressive degradation, and the time to fracture has an exponential survival function F̅(s) = exp(−ζs) with hazard rate ζ = − ln G(y₀) = (α/y₀)^β.

Finally, it is helpful to consider the form of the log-hazard function for our model. Letting h(s) denote the hazard function, we have

$$\text{ln}h(s)=\beta [\text{ln}(\alpha )-\text{ln}(y_0)-\lambda s].$$ (7)

The log-hazard is seen to be rising, constant, or falling with s according to whether λ is negative, zero, or positive.

5. Application to First and Second Fractures in the SOF Study

Model estimation

Our time-to-fracture data are conventional right-censored time-to-event data. We employ the maximum likelihood method to estimate our model using the formulas for the log-survival function in (5) and the log-hazard function in (7). The optimization required in our estimation employs the gradient maximum likelihood subroutine ml in Stata 12.0 (Stata Corporation, College Station, TX, USA). This routine also produces estimated asymptotic standard errors for parameters based on an estimated Hessian matrix for the likelihood function.

The censored time-to-fracture data only allow us to estimate two of the four parameters of our TR degradation-shock model. To connect the parameters to covariates, we choose a logarithmic link function ln(y₀) for the initial skeletal strength and an identity link function for the degradation rate parameter λ. The covariates are enumerated in the next subsection. Parameters α and β of the shock process are each set to 1, without loss of generality. To see why all four parameters cannot be estimated, refer to the mathematical form of the log-survival function (5). When initial skeletal health y₀ is given a logarithmic link function and rate parameter λ is given an identity link function, we see from the mathematical form that changing the value for α would only change the intercept of the regression function for ln(y₀). Likewise, changing the value for β would only change the regression coefficients of ln(y₀) and λ by a fixed multiple.

Covariates

Given risk factors for hip fractures identified in the literature, we chose to examine the following potential predictors: age; total hip and femoral neck BMD; fall and faint histories; depth perception; body mass index (BMI); co-morbidities associated with impaired mobility, namely, hyperthyroidism, stroke, Parkinson’s disease, rheumatoid arthritis, and diabetes; use of vitamin D and calcium supplements; estrogen therapy; weight change; smoking; and exercise. The specific covariates selected from the SOF Study to cover these risk factors appear in Table 1. A number of potential covariates could not be considered because they had large numbers of missing values.

Table 1.

Covariates from the SOF Study used for the investigation of first and second fractures.

Variable in regression	Variable label
thyroid	Doctor ever told you have high thyroid?
stroke	Doctor ever told you have had a stroke?
Parkinson	Doctor ever told you have Parkinson’s disease?
arthritis	Doctor ever told you have arthritis?
diabetes	Doctor ever told you have diabetes?
#faint	Number of times fainted in last 12 months
#fall	Number of falls in last 12 months
bmi	Body mass index (kg/m2)
age	Age at visit 2 (baseline visit)
hipBMD	Total hip BMD (g/cm2)
fnBMD	Femoral neck BMD (g/cm2)
vitamin D	Currently taking Vitamin D once per week
Tums	Currently taking Tums once per week
estrogen	Currently taking estrogen pills
mndepth	Mid near depth perception
lndepth	Low near depth perception
wt-change	Weight change since 25 years old (kgs)
smoke	Smoking status (never, past, current)
exercise	Take walks for exercise?

First fractures

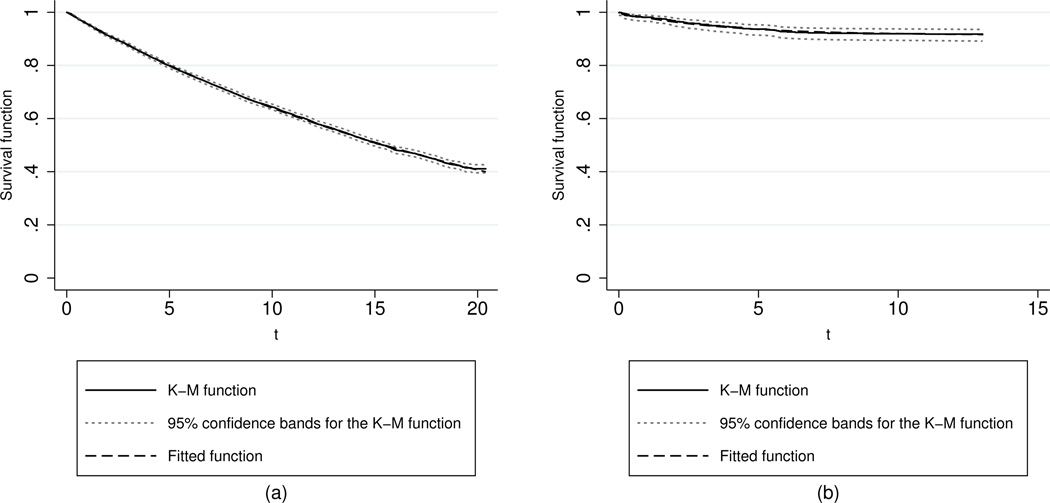
We have applied the TR degradation-shock model in (5) to the SOF data for first fractures. As an initial check on fit, we have estimated the model without covariates. Panel (a) of Figure 5 shows an overlay of the Kaplan-Meier and fitted survival functions, together with 95% confidence bands for the Kaplan-Meier function. The fit is so close that the curves are almost indistinguishable. Moreover, the TR regression output for the fitted model (without covariates) shows that the λ parameter does not differ significantly from zero (P-value= 0.668) and, hence, a pure exponential survival distribution provides a reasonably good fit to the data. Recall that the exponential model is a special case of the TR degradation-shock model being proposed here. Shortly, we add covariates to this model and find a revised version of the fitted model in which significant differences do appear for subpopulations of patients, including some material departures from the pure exponential model.

Figure 5.

Plots of the Kaplan-Meier and fitted survival functions, as well as the 95% confidence bands for the Kaplan-Meier function for (a) first and (b) second fracture times based on the TR degradation-shock model without covariates. The fitted model for second fractures has a large proportion of subjects who will not experience a second fracture (a large cure rate).

The TR output for first fractures in the SOF study based on the exponential degradation-shock model is shown in Table 2. The full regression model started with the covariates in Table 1 for each of parameters ln(y₀) and λ. Covariates were then subjected to backward elimination by successive culling of the covariate with the largest P-value. Culling proceeded until all P-values were smaller than 0.10.

Table 2.

Threshold regression output for first fractures in the SOF study based on the degradation-shock model in (5).

1st fracture	Coefficient estimate	SE	P-value
Regression for baseline log-skeletal strength ln(y0):
stroke	−0.317	0.104	0.002
Parkinson	−0.457	0.220	0.037
arthritis	−0.126	0.038	0.001
diabetes	−0.349	0.073	< 0.001
#fall	−0.013	0.007	0.063
age	−0.016	0.006	0.010
hipBMD	2.029	0.286	< 0.001
fnBMD	1.632	0.339	< 0.001
vitaminD	−0.081	0.037	0.028
estrogen	0.375	0.099	< 0.001
lndepth	−0.119	0.050	0.016
Intercept	2.005	0.500	< 0.001
Regression for degradation rate λ:
age	−0.003	0.001	0.001
estrogen	−0.037	0.010	< 0.001
wt-change	−0.001	< 0.001	0.001
Intercept	0.179	0.060	0.003

Note: The top section of output gives the fitted regression model for baseline log-skeletal strength ln(y₀). The bottom section gives the fitted regression function for degradation rate λ. The sample size is 6,948.

The top section of Table 2 gives the fitted regression model for log-skeletal strength ln(y₀). The indicators for stroke, Parkinson’s disease, arthritis and diabetes all have significant negative effects, although the P-value for Parkinson is weak at 0.037. All of these key diseases tend to reduce skeletal strength. The P-value for #fall is not significant at the usual 0.05 level. Covariate age has the anticipated negative association with skeletal strength. The two BMD measures, hipBMD and fnBMD, are both statistically significant with regression coefficients that are large and positive. These two variables are highly correlated (r = 0.86), which is not surprising, but it is apparent that their signals are sufficiently strong and separate that they overcome this collinearity. Both variables are subject to measurement error but each conveys independent information about skeletal strength and, hence, both contribute significantly to the TR regression model. Using a sample size analogy, the two BMD readings are the equivalent of having two sample measurements rather than one. The finding suggests that clinicians should consider both BMD readings in judging current skeletal strength. It is consistent with the recommendation of assessing BMD at the femoral neck, total hip and lumbar spine for diagnosis of osteoporosis (T-score at any site of −2.5 or below) as this is a treatment threshold based on the 2013 U.S. National Osteoporosis Foundation (NOF) Clinician’s Guide to Prevention and Treatment of Osteoporosis [30]. Moving on to the next covariate, we find that indicator variable vitaminD has a weak P-value (0.028). Its negative coefficient may be a case of confounding by indication. The estrogen indicator has a large positive effect. The indicator for the depth perception covariate lndepth has a weak P-value (0.016).

The bottom section of Table 2 gives the fitted regression function for the rate of decline λ. The regression coefficient for age (in years) in this latter regression function is significant and negative. The negative sign indicates that older subjects tend to experience a higher rate of progressive deterioration in skeletal strength, which is a plausible finding. Interestingly, whereas current use of estrogen gives a subject better skeletal strength, the significant negative coefficient of the estrogen indicator for the rate parameter suggests that this initial gain is lost with the passage of time. There are two explanations for this effect, both raised by the medical literature [1, 31–32]. The first explanation is that the beneficial effect of estrogen therapy declines with continued use. The second explanation, and the more plausible in our view, is that some subjects on estrogen at baseline discontinue using it because of the recognized risks for cardiovascular disease and breast cancer that are posed by its long-term use. Discontinuation of the therapy reduces those risks but exposes subjects to elevated risk of fracture with time; hence, the negative coefficient for estrogen in the rate parameter regression. The next insight from the bottom section of Table 2 is that larger weight change since age 25 (variable wt-change) tends to accelerate the decline of skeletal strength. Finally, although the intercept term for parameter λ is positive, the aggregate negative influences of the covariates is sufficient to make the estimated rate parameter λ negative in 88 percent of cases. The estimates of λ vary from −11.1% to 1.6% per year.

Second fractures

The TR degradation-shock model in (5) has also been applied to SOF data for second fractures. Again, as an initial check on fit, we have estimated the TR degradation-shock model without covariates. Panel (b) of Figure 5 shows an overlay of the Kaplan-Meier and fitted survival functions. As for first fractures, the model’s fit is so close that the curves are almost indistinguishable. Moreover, the TR regression output for the fitted model (without covariates) shows that the λ parameter is significantly positive (0.265) and differs significantly from zero (P-value< 0.001). The positive estimate of λ yields a survival distribution with a large cure rate component, estimated at 91.4%. In other words, it appears that only 8.6% of subjects would go on to eventually have a second fracture. Even though the fitted models in Figure 5 are estimated without covariates, the fits are strikingly good. The inclusion of significant covariates will explain some of the remaining wiggles in the fit. The fact that the fit of the TR degradation-shock model to second fractures yields a substantial cure rate is an intriguing finding that we return to discuss after fitting the model with covariates.

Threshold regression output for second fractures in the SOF study based on the TR degradation-shock model in (5) is shown in Table 3. Again, parameters α and β have been set to 1 in this application. As with first fractures, the full regression model started with the covariates in Table 1 for each of parameters ln(y₀) and λ. Covariates were then subjected to backward elimination by successive culling of the covariate with the largest P-value. Culling proceeded until all P-values were smaller than 0.10. The top section of output gives the fitted regression model for log-skeletal strength ln(y₀). All of the covariates (bmi, fnd and mndepth) remaining in the regression function for ln(y₀) have significant and material positive effects on skeletal strength. Note that for second fractures, it is only the femoral neck BMD that enters the regression function as a significant predictor of baseline skeletal strength. The bottom section gives the fitted regression function for the rate of decline λ. The regression coefficient for bmi in this latter regression function is −0.0240 and is marginally significant (P-value= 0.057). The estimated values of λ are positive for all but the 15 most obese subjects who have the highest values of bmi. This coefficient indicates that obese patients experience progressive deterioration in skeletal strength with respect to a second fracture.

Table 3.

Threshold regression output for second fractures in the Study of Osteoporotic Fractures based on the degradation-shock model in (5).

2nd fracture	Coefficient estimate	SE	P-value
Regression for baseline log-skeletal strength ln(y0):
bmi	0.139	0.070	0.049
fnBMD	5.562	2.146	0.010
mndepth	0.881	0.326	0.007
Intercept	−3.035	1.728	0.079
Regression for degradation rate λ:
bmi	−0.024	0.013	0.057
Intercept	0.829	0.319	0.009

Note: The top section of output gives the fitted regression model for baseline log-skeletal strength ln(y₀). The bottom section gives the fitted regression function for degradation rate λ. The sample size is 519.

Model checking

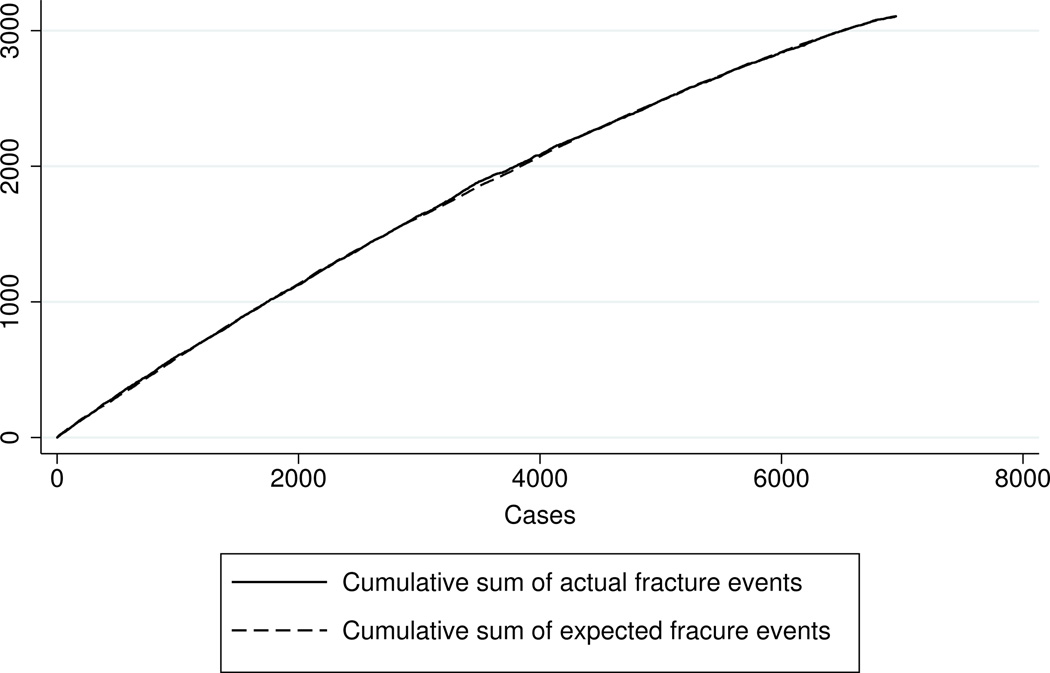
We have made a number of graphical checks on the goodness of fit and discriminating power of our regression models. The analysis makes use of martingale residuals of the form r_i = f_i − e_i, where f_i is an indicator variable for observed fracture or not (f_i = 1 or 0) and e_i is an unbiased estimate of f_i calculated from the model for the given covariates of patient i, i = 1,.…, n. Our graphical analysis plots the ordered pairs (f_i, e_i) against a selected covariate of interest. Figure 6 shows one plot that illustrates the model’s fit with respect to skeletal strength y₀ for first fractures. Recall that ln(y₀) is a linear combination of several significant risk factors for first fracture as shown in the top section of Table 2. The horizontal scale of the graph is the rank of the patient when patients are ordered by their fitted values of y₀. The vertical scale represents cumulative sums. One curve corresponds to the cumulative sum of actual fracture events, i.e., the cumulative count of f_i. The other curve is the cumulative sum of the estimates e_i. The plot reveals both the calibration and predictive power of the fitted model. The extent to which the two curves track each other is an indication of the calibration of the regression model with respect to the covariate being examined (y₀ in this case); in other words, the extent to which the estimates are unbiased across different levels of the covariate. The distance between the two curves corresponds to the cumulative sum of the martingale residuals. In Figure 6 it can be seen that the actual and estimated curves for y₀ track each other so closely that they are almost indistinguishable. Thus, the model is well calibrated with respect to skeletal strength. The extent to which the curves bend or arch toward the upper left-hand corner of the graph measures the extent to which the ordering variable is predictive of first fracture. A sharp bend would indicate strong predictive power; a nearly linear plot, little predictive power. Figure 6 shows only a modest bend and, hence, tells us that the covariates estimating skeletal strength in our regression model, although statistically significant, offer only modest predictive power.

Figure 6.

A plot showing the calibration and predictive power of the model for first fracture. The curves compare the cumulative sum of actual and expected fractures, based on martingale residuals, when patients are ranked by their estimated skeletal strength y₀.

Simulation study

The performance of the proposed maximum likelihood estimators has been assessed through a simulation study. The range of parameter values for ln(y₀) and λ are roughly those encountered in our study for first fractures. Censoring times are taken to be independent and uniformly distributed over the interval from 0 to 20 years. Using 1,000 replications, for both small and large samples (100 and 1,000, respectively), the results for parameter estimates, standard errors and coverage probabilities show very satisfactory performance (data not shown). In particular, the estimated bias is uniformly small and the empirical coverage probabilities are very close to their 95% nominal value, under various degrees of censoring. As expected, the results become better when the sample size increases.

6. Discussion and Concluding Remarks

In our application, we chose to give regression structures to parameters ln(y₀) and λ and to fix α and β at 1 because only two of the four model parameters can be estimated from censored time-to-fracture data. To elaborate on the implications of these choices, we mention that parameters of the shock process can be estimated if we are prepared to fix parameters of the degradation process. To illustrate with a simple example, if we fix initial skeletal strength y₀ at 1 and estimate ln(α) using the same covariates as shown for ln(y₀) in Table 3, the same regression function is obtained except for the regression coefficients of ln(α) having the opposite sign of those for ln(y₀). This correspondence follows from equation (5) where the survival function is seen to depend on α and y₀ only through the ratio α/y₀. In terms of logarithms, the ratio becomes ln(α) − ln(y₀). Hence, if one of these parameters is fixed at 1 (so its logarithm is zero), the other shows the same variation with covariates but with opposite sign. Hence, by fixing initial health level y₀ at 1, we shift the effects of these covariates to the shock distribution in a mirror-image fashion. In all likelihood, pushing the covariate effects from one parameter to another does not describe the actual causal forces at work – reality is somewhere in the middle. For instance, among the covariates bmi, fnBMD and mndpth in the top section of Table 3, higher femoral neck BMD likely strengthens the skeleton directly while better mid-near depth perception tends to lower the incidence of shocks because vision is better. Higher body mass index has a mixed effect because it may be associated with greater skeletal strength but also is seen to accelerate degradation of strength through the rate parameter λ.

Second fractures present the interesting result that a large proportion of patients (over 90 percent) seem immune to experiencing a second fracture. Because the parameters of the shock process (α and β) have been arbitrarily fixed, the immune proportion (a so-called cure rate) is produced by a degradation rate parameter λ that is positive, implying that skeletal strength improves with time. On the surface, this result seems implausible. But it must be kept in mind that our skeletal strength measure is a latent construct. Because initial strength y₀ and its rate of change λ are free parameters that are estimated, while the shock parameters α and β are fixed to 1 in advance, the unit of measure of the skeletal strength scale is essentially calibrated by the shock process. It is reasonable to assume that most patients who experience a first fracture will take remedial steps to avoid a second fracture. These steps might include such actions as taking prescribed medications, receiving physical therapy and changing diet to improve bone strength or at least to slow its degradation. The list of actions might also include life style changes such as being more cautious in ambulation, using walking aids, correcting eye sight, and generally avoiding exposures to large shocks or traumas. Of course, the array of remedial actions chosen by patients and the effectiveness of these actions in providing greater protection will vary from one patient to another so their propensity for fractures will vary.

The TR degradation-shock model is a new and promising model for understanding skeletal fractures in elderly women. It is novel and sensible in the way it forms a composite of two distinct forces that are at play in this phenomenon, namely, chronic progressive degradation of the skeleton with aging and exposure of the body to shocks and traumas of varying timing and magnitude. Our current TR degradation-shock model treats the degradation component as deterministic whereas in reality it may be a stochastic process like the shock process. Further advances are needed in both modeling and data gathering for a real statistical understanding of osteoporosis, which remains a debilitating disease that many people will still experience in old age.