Abstract
Abstract: Better understanding of bacteria environment interactions in the context of biofilm formation requires accurate 3-dimentional measurements of bacteria motility. Digital Holographic Microscopy (DHM) has demonstrated its capability in resolving 3D distribution and mobility of particulates in a dense suspension. Due to their low scattering efficiency, bacteria are substantially difficult to be imaged by DHM. In this paper, we introduce a novel correlation-based de-noising algorithm to remove the background noise and enhance the quality of the hologram. Implemented in conjunction with DHM, we demonstrate that the method allows DHM to resolve 3-D E. coli bacteria locations of a dense suspension (>107 cells/ml) with submicron resolutions (<0.5 µm) over substantial depth and to obtain thousands of 3D cell trajectories.
OCIS codes: (090.1995) Digital holography, (100.2980) Image enhancement, (100.6890) Three-dimensional image processing, (180.6900) Three-dimensional microscopy
1. Introduction
It has attracted significant interests recently in resolving key processes involved in biophysical interactions between bacteria and their constantly changing environment [1–6]. These processes include three-dimensional (3-D) bacterial locomotion, swarming behaviors and transport dynamics near complex boundaries such as surfaces or interfaces with heterogonous topology, roughness, and energy landscape, which often occur in a wide range of spatial and temporal scales, ranging from sub-microns to millimeters and from microseconds to hours. Observations of these highly 3-D dynamic processes and interactions require tools capable of resolving these fine spatiotemporal scales in a 3-D volume.
The optical microscope has traditionally been employed to study cell morphology. In a conventional optical microscope, as the power and lateral resolution increase, the depth of field decreases, e.g. to 12μm at 10X and to 2μm at 40X [7], which limits one’s ability in resolving micro-/nano-scales structures over a large depth. Employing tomographic principle to image micro-structures aligned in 3-D thick sample and to extend the depth of field, several techniques has been developed. Greenberg and Boyde [8] first employed multiple angle illumination and a single lens to collect projections at multiple viewing angles, which allows them to extend the depth of field to 150μm. The technique has been further extended to confocal scanning microscopy [9], transmission electron microscopy [10], and later soft x-ray microscopy [11] as well as Electron Microscopy [12]. However, since these techniques require the sample to be stained or “frozen” in crystalline structures, they are not suitable for imaging live cells and quantifying their dynamic interactions.
Confocal microscopy [13] using point source illumination and a spatial filter eliminates the out-of-focus light in a specimen thicker than the focal depth and hence can reach super resolutions exceeding diffraction limits. Combining with scanning techniques, the confocal microscopy have transformed into 3D imaging standards, which include confocal laser scanning microscopy [14,15], and spinning disk confocal scanning microscopy [16]. Albeit the high spatial resolutions, slow temporal resolution limits the applications to quasi-stationary processes. Circumventing this limitation, Berg [17] has developed a 3D tracking microscope to provide Lagrangian observation of a single bacterium in 3D. The microscope can achieve tracking accuracy of 1 bacterial diameter and tracking range of 1mm in all directions. It has been successfully applied to chemotaxis study of E. coli bacteria [18] and later bacterial motility close to a solid surface [19]. Although this technology had revolutionary impacts on our ability in studying bacterial motility, robust statistics from individually collected 3D trajectories is a tedious and time consuming task.
Being an inherent 3-D recording technique and its ability in recording series of holograms digitally and reconstructing holograms numerically, digital holography paves the way for studying many dynamic phenomena [20]. However, the limited spatial resolution of the earlier digital holography systems [20] that are composed of lens-less recording cameras and the laser optics have proven difficult to observe micro-scale particles over substantial depth [20]. To circumvent the recording resolution limitation, Xu et al. has developed lens-less digital holography with a point illumination to visualize intra-cellular structure of a marine diatom [21]. Later, the technique has been implemented in a submersible to track marine particulates [22] with limited success. Using partial coherent illumination and multiple projections, Ozcan et al. [23–27] have developed several portable devices to screen and detect cells based on partial coherent holography. Amid numerous variations, their fundamental system consists of a large format sensor as the substrate, over which the cells are flowing, and a point source with partial coherence [28] that illuminates the shallow suspension from multiple angles. With the advantage of high resolution digital camera and strong near field scattering, they have successfully resolved cells with resolutions of ~1μm. However, the drawbacks of lens-less systems are the shallow sample depth (<20μm) with low concentration of sample cells (<105 cells/ml) and complicated post data analysis, since the magnification of the hologram in lens-less holography depends on axial distance of the object and the source of the reference beam from the hologram [20].
The simple and straightforward inline Digital Holography Microscopy (DHM [7],) has proven to be more versatile and robust. In this method, the sample is illuminated by a collimated coherent light source and the holograms are imaged by a lens or a microscope objective. Sheng et al. has demonstrated that the recorded image is a magnified hologram [7]. It has been show that it has substantially improved the spatial resolution while maintaining large measurement depth [7]. Several other DHM systems based on Mach-Zenhnder interferometry [29–34] and phase shifting interferometry [35–38] have been developed. Among them, Rappaz et al. [34] have successfully measured micro-scale surface morphology of a metastasized ovarian cancer. Although these methods have demonstrated unique capabilities, their primary applications focus on single stationary cell or particles in suspension with low concentrations. Resolving both kinematic and morphological information of many cells concurrently may be difficult with the aforementioned DHM methods.
A simple in-line DHM developed by Sheng et al. [7] has been consistently tracking thousands of particles and micro-organisms simultaneously in a dense suspension under environmental conditions and revealed key microbial processes based on robust statistics [7,39–49], in measuring 3-D flow fields around free swimming micro-organisms or small fish [41,50], and in measuring 3D turbulent wall bounded flows [51–53]. The technique has proven to reach the spatial resolution of 200nm over substantial depth [7]. Amid the success in planktons and solid particles, imaging moving bacteria in a 3-D volume has proven to be difficult. Major difficulties lie in recording quality bacterial holograms, since: (i) The contrast of the index of refraction of bacteria ( [54]) to that of the water ( ) is small, i.e., the light scattered from a bacterium is much weaker that from a solid particle with equivalent diameter. Recording the interference pattern generated by a single bacterium cell is not trivial; (ii) Small size of cell, typically 1-2 μm, reduces the scattering efficiency substantially; (iii) As the scattering of particle decreases, the intrinsic noise of the coherent light source becomes stronger than those scattered from bacterial cells. These contribute to lower SNR of the recorded holograms and render reconstruction of 3-D bacteria images difficulty.
In this paper, we present the first of its kind DHM technique with a novel de-noising algorithm that is capable of tracking bacteria over substantial depth in a dense suspension (107 cells/ml) over long period of time (>10min) with high temporal (up to 3000 fps) and spatial resolution (<0.5 μm). The de-noising algorithm is described in §2, followed by the details about microfluidic experiments in §3. The results on de-noising efficacy, spatial resolutions, and its impact on 3D bacterial motility measurement are provided in §4, before we briefly conclude in §5.
2. Methods and methodology
2.1. Brief background on digital holographic microscopy
Inline Digital Holography Microscopy (DHM) has recently been successfully used in providing 3D image of micro-organisms with high spatial resolution [41,46,55], tracking their 3-D movement and behavior within a dense suspension [7,39,40,49,56], and measuring flow around the free swimming organisms [41,50,57]. Here an in-line approach for DHM is used, in which the sample is illuminated by a collimated laser beam and the hologram formed outside of the sample volume is recorded. The optical field at the hologram plane, i.e. the interference between the undisturbed reference wave, , and the scattering from the micro-organisms , is described as , and the intensity distribution of interference patterns, i.e. the recorded hologram, is . The first term represents the intensity generated by the reference beam. The second and third terms represent the interference patterns between scattered and reference light, of which the 3D information of particles, i.e. shape and 3D location, is recorded. The second term registers the virtual image and the third encodes the real image. The interference of the objective wave produces speckle noises, which contributes to the granular background image of the holographic reconstruction. It has been shown that the last term reduces the signal to noise ratio (SNR) when the scattering of particles is strong and the density of particles is high [58,59]. Differing from lens-less digital holographic microscopy, current DHM records the interference pattern via a microscope objective (a system sketch is shown in Fig. 1 and variants of system are shown in Sheng et al. [51]). Sheng et al. [7] have shown that the image recorded is in fact a magnified hologram, , where is the magnification, is the irradiance of the original hologram, and is the DHM recording. Several groups have demonstrated that inline DHM can reach ~2μm in all directions over substantial depth [7,20,39,40,56]. In this paper, we will further demonstrate that DHM with the proposed de-noising method can resolve 3-D bacterial motions with spatial resolution down to 0.2μm in the lateral directions and 0.5 μm in the depth direction.
Fig. 1.
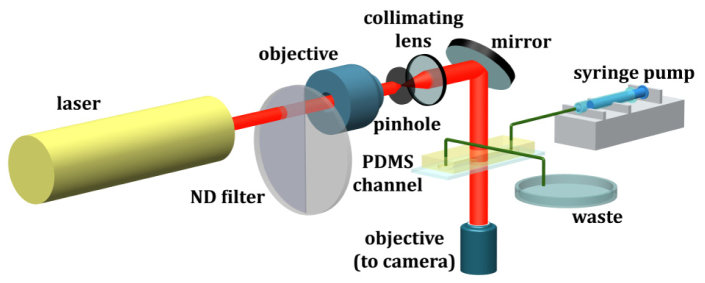
Setup of Digital Holography Microscopy (DHM) and microfluidics platform.
The original 3D optical field containing the scattering of particles needs to be reconstructed from the recorded hologram. Conventionally, this 3-D field is reconstructed optically by illuminating a hologram with a conjugate reference wave, and is scanned atdifferent depths by a digital camera [42,50,60,61]. In DHM, the reconstruction and subsequent scanning are performed numerically: To obtain a 2-D optical field, , at a distance to the hologram plane, z, the recorded hologram, , is convoluted with an impulse response function, . This impulse function represents the diffraction and propagation of light from a point source in a homogeneous medium. It can be approximated as either Kirchhoff-Fresnel or Rayleigh-Sommerfeld solutions (Details in [20]). In practice, Fresnel kernel with paraxial approximation, where is the wave number and is the wave length, is often used owing to its simplicity. The reconstructed optical fields at the distance, z, to the hologram plane, can then be obtained.
2.2. Noise in bacterial hologram recorded by digital holographic microscopy
Observing submicron scale object of a diameter less than 1 using DHM is non-trivial. Tracking these objects in 3D with sufficient resolution capable of resolving both 3-D position and the shape is no small task. For those cells with low contrast of index of refraction such as E. coli bacteria, to the best of our knowledge, there are no existing methods that can successfully track them simultaneously in dense suspensions in 3D with the resolution presented in this paper. It is primarily because the presence of background noises overwhelms the scattering generated by the bacteria. It is known that the intensity of the light scattered form particles strongly depends on the size and the contrast of the index of refraction between the particle and the medium. Since the index of refraction of a bacteria ( [54],) is close to that of the medium ( ), the intensity of the light scattered from a bacterium is much smaller than that from a solid particle with the same size. To separate and remove the noise from the holographic interference signal of bacteria, we must first understand the noise and bacterial scattering signal.
The intensity distribution of a hologram is described as the following,
| (1) |
where is intensity distribution of noise and represents that of light scattering from bacteria. The subscripts H, B, and N represent original hologram, bacteria, and noise respectively. Note that both noise and bacteria intensities are time varying functions. From our observations, we summarize the following two characteristics of noise and bacterial scattering:
(i) Signal to Noise Ratio (SNR) is much less than one, i.e. , where denotes average over the entire hologram. The SNR of bacterial hologram differs greatly from that of the solid particle hologram. Figures 2(a) and 2(d) show two original holograms of E. coli and 1 solid particle (Polystyrene, Thermo Scientific) in suspensions with the equivalent concentration. The holograms are recorded at the magnification of 40X using the DHM system elucidated in Fig. 1. While the interference pattern of solid particles is clearly observable, that of E. coli is indistinguishable from the large scale intensity variations. It demonstrates that the low SNR of bacterial holograms contributes substantially to the low image contrast in the reconstructed images. This very problem imposes major difficulties for existing DHM techniques and renders them ineffective in bacterial holography.
Fig. 2.
Portion of original and de-noised sample holograms of (Left) E. coli and (Right) solid particles. (a & d): Original holograms. (b & e); holograms de-noised with the conventional time-averaging technique; (c & f): holograms processed with the correlation-based ensemble-averaging technique.
(ii) Scale separation between interference pattern by bacteria and spatial variations of hologram noise, i.e. the size of the interference patterns generated by bacteria is much smaller than the characteristic length scale of background noise. The size of the interference pattern in the in-line holography depends on the size of particles, , and the distance to the hologram plane, . One can estimate the characteristic size of the interference pattern of the bacteria using the airy disk of an equivalent sphere as . For instance, in theory the interference pattern of an E. coli bacterium recorded at 40X and at the distance of with a He-Ne laser ( ) is estimated as ~39 μm (or 0.1 size of hologram). In practice, due to the low scattering efficiency by bacterium, the size of the interference pattern is expected to be only a fraction of airy disc to about 5-10 . In comparison, the length scales of the interference or intensity variations due to the presence of laser instability and multiple internal reflections are much larger. This scale separation between the signal and noise are exacerbated in DHM recordings, which are elucidated clearly in sample holograms [note the scales of background intensity variations in Figs. 2(a) and 2(d)].
2.2.1. Noise characteristics in digital holographic microscopy
It is necessary to understand further on noise characteristics in DHM before effective mitigation methods can be developed. The noise in DHM is composed of speckle noise, , and system noise, ,
| (2) |
The speckle noise term, , is inherent to any imaging techniques using coherent light sources, such as digital holography, and manifests itself as smaller granular patterns in a hologram. The speckle noise in a hologram is often assumed to be Gaussian and spatiotemporally random. The speckle noise often carries lower energy content and hence has low average intensity, i.e. , where denotes spatial average over the entire hologram. The latter term, , however, is not random but coherent in both spatial and temporal domains and often carries high energy content that may overwhelm the interference patterns generated by low intensity bacterial scattering. The system noise often manifests itself in spatial domain as very large scale intensity variations (elucidated in Figs. 2(a) and 2(d)) due to the presence of defects or dust particles along the optical path. Note that the interference patterns of solid particles are clearly observed over the noise interference [Fig. 2(d)], whereas the bacterial signal is completely overwhelmed by these system noise [Fig. 2(a)]. We have found that the system noise is primarily generated by multiple internal reflections within the optical system. After applying anti-reflection coating over optics in our DHM system and surfaces of the microfluidics, the fringe visibility is substantially improved. However, such an improvement is still not significant enough to render substantial effects on bacterial fringe visibility. It can also be argued that due to inherent fluctuations in any laser systems it is less likely the system noise can be reduced by selecting a stable laser. Owing to the property of scale separation of the system noise, , and subsequently can be estimated by low pass filtering over the original hologram,
| (3) |
where the symbol “ ” represents low pass filter operation, is the convolution operator and denotes the spatial representation of a low pass filter with the cut-off length scalesof and in the and directions respectively. These cut-off length scales can be physically determined by the size of the bacterial interference patterns. Due to the laser instability, the background noise, , is time dependent and but temporally correlated. The correlation of in two holograms at the time frame of and can be estimated as
| (4) |
where is the correlation coefficient. The correlation varies between 0 and 1, with 0 indicating not correlated and 1 identical. We have applied Eq. (4) to a time series of bacterial holograms [a sample one is shown in Fig. 2(a)] to demonstrate temporal correlation of background noise among holograms (sample correlation profiles are shown in Fig. 3 ). The cut-off length scales used are 29μm (or , where is the field of view in the x direction). Figure 3(a) shows the correlation coefficients between the time frame, , and its neighboring time frames, i.e. or . The correlation fluctuates around 0.92 and 1. As the delay, , increases, the correlation decreases gradually. As further increases, the correlation recovers and oscillates with a period of ~150 s. The same trend can also be observed in Fig. 3(b), where the selected correlation profiles at various along the entire series are computed with a delay, , of [-250, 250]. It is shown that correlation profiles close to each other within a range of ~60s have similar temporal coherence, as shown as the clustered correlation profiles plotted at . As time evolves, a new cluster of correlation profiles emerges. This trend can be attributed reasonably to slow temporal drift and fluctuations in longitudinal modes existed in the laser source.
Fig. 3.
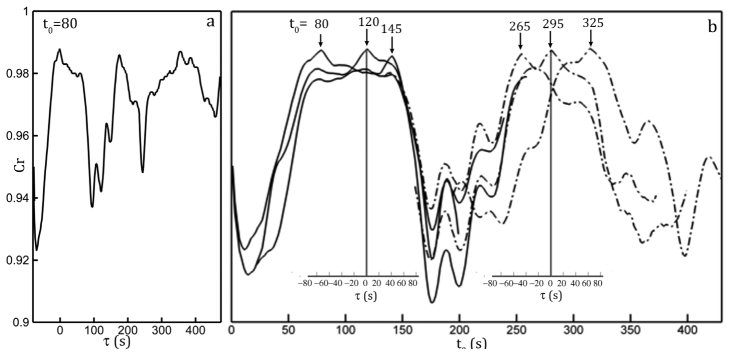
The correlation coefficient profiles smoothed by a 3-point moving average. (a) The correlation coefficient profile calculated with Eq. (3) between the hologram recorded at and its neighboring holograms within the temporal shift, , ranging s. (b) The correlation profiles for holograms recorded at various time frames shown on top of each profile. The main horizontal axis shows the absolute recording time, . Inset axes show the time delay, , with respect to the selected time frame, , shown the Inset vertical axes as . Only axes corresponding to profile centered at are shown for clarity.
2.2.2. Development of de-noising algorithm
Effective de-noising for DHM can be achieved by subtracting each hologram with an appropriate background noise hologram. Conventionally, the noise hologram is estimated by simply averaging over a time series of holographic recordings, i.e.
| (5) |
In this method, the noise is assumed random and stationary. The method is effective to remove a statistically stationary background noise, such as spatial variations in light illumination and scattering from the stationary dust particles along the optical path. As demonstrated in Fig. 2(e), for DHM with high scattering efficient the method shows great efficacy in removing large scale spatial variation in Fig. 2(d); whereas for DHM with low scattering signal, the method has practically no impact. Another method to estimate the noise is to record a background hologram. But the method shares the same drawback with time-averaging method.
Demonstrated above, for removing un-stationary noise from bacterial holograms, a new noise estimation algorithm must be developed. Based on the two properties of bacterial holograms, we can estimate the noise of each hologram for a given time frame along a series of recordings using conditional sampling:
| (6) |
where is the threshold, and represents the averaging operation over the time delay, . Equation (6) represents that the noise hologram at time, , can be estimated by ensemble averaging those original holograms with the similar interference background defined by the condition, . The de-noised hologram, , for a given time frame is obtained as
| (7) |
Note that to obtain a de-noised hologram with good fringe visibility, proper threshold value, , need to be determined. An appropriate threshold value should be lower enough to include sufficient holograms for averaging, while it should be high enough to exclude those less correlated holograms from contaminating the estimation. Typically, we select a value between 0.95 and 0.99 that includes at least 100 holograms. It needs to point out that computing is time consuming. A parallel computing algorithm has been developed to reduce computation cost using a 16-node cluster. In practice, we calculate coefficients within a range of τ, since background noise slowly de-correlates over time. We summarize the algorithm as the following:
-
1.
Record a time series of holograms, , totaling number of frames. To produce a robust estimation for each hologram, the total number of frames must be big, e.g. ;
-
2.
Compute correlation coefficient matrix, , where , and is the recording interval. The correlation is computed using Eq. (4) over low pass filtered holograms, . The coefficient matrix will be ;
-
3.
Select the n-th hologram, ) to compute background hologram, );
-
4.
Search through correlation matrix and identify a list of holograms, m, within which the condition is satisfied.
-
5.
Estimate the background noise, ), by ensemble averaging the list of holograms above, , where M is the total number of the holograms satisfying the condition in Step 4;
-
6.
De-noise the hologram by ;
-
7.
Repeat Step 3-6 for entire sequence of holograms.
3. Experimental setup
3.1 Microfluidics platform
The experimental setup includes a DHM integrated and a microfluidics platform (Fig. 1). The platform is designed to investigate interactions of bacteria in a dense suspension with the mechanical and chemical environments [1]. The polydimethylsiloxane (PDMS) microchannel is manufactured using soft lithography technique [62]. Briefly, the fabrication procedures are the following: (i) negative mask containing the top view of the microfluidic device is created by high resolution printing (10,000 DPI); (ii) deposit a thick layer of SU8-2050 negative photoresist (MicroChem, Inc) on a 4” silicon wafer; (iii) transfer features to the photoresist uses photolithography; (iv) the PDMS microfluidics is created by molding the device out of the master and bonded with the glass substrate by O2 plasma activation. To reduce background noise, we bond the microchannel with a glass slide coated with MgF2 anti-reflection layer. Bonding with the AR coated substrate is temporary and device must be used within 20-minute of bonding. The straight microchannel has the dimension of 3 mm × 40 mm × 200 μm, the latter being the depth.
3.2 Digital holographic microscope
The DHM includes a CW (continuous wave) He-Ne laser, collimating optics, an inverted transmission microscope, and recording CCD camera (Fig. 1). We illuminate the microchannel with a collimated laser beam generated by a 7mW He-Ne laser ( ). The initial beam is filtered and collimated into a beam with the diameter of 5mm by a 20X objective (Edmund Scientific), a 25- pinhole (Thorlabs), and a 25mm diameter doublet as the collimating lens ( , Newport Inc). A 1/20-λ aluminum mirror guides the horizontal beam downward into an inverted Nikon microscope (Nikon TS-100). To record bacteria holograms, an objective at the magnification of 40X (Nikon Super Plan Fluor ELWD, NA = 0.60) is used. The objective is focused on the plane 5 away from the bottom of the microfluidics. The holograms are recorded by a 2K × 2K CCD camera (Imperx 4M15L) with a pixel resolution of 0.185 /pixel, which renders the lateral resolution of 0.2 for simplicity, and were streamed continuously at the rate of 15 fps to a data acquisition computer. The exposure time was 60 . To achieve robust estimations for each hologram in a series, the typical recording lasts about 20 minutes, totaling 18,000 holograms/acquisition.
3.3. Materials and methods
3.3.1 Bacterial culture
The bacteria strain used is wild type E. coli strain AW405. It has a rod-like shape with 1.5 μm in the major axis and ~0.8 μm in the minor axis. AW405 was grown in a 10 ml flask of LB medium following inoculation of 100 short-term stock stored at −20 °C freezer. On the day prior to experiments (at least 24 hours), the strain was grown in LB medium at 30 °C until the culture reached stationary phase (OD600 = 1.2). The 100 μl of this culture were used to inoculate 10 ml of Tryptone medium (1% tryptone, 0.5M NaCl) and grown at 35 °C to mid-logarithmic phase (OD600 = 0.45). Both culturing procedures were performed by an orbital shaker at 120 rpm (Model 980184, Talboys). Cells were then washed twice by centrifuging at 2000 rpm (~850 g) and re-suspending in the motility buffer (10−2 M potassium phosphate buffer; pH = 7.5) containing 10−4 M EDTA [63]. The suspension, which had a concentration of ~107 cells/ml was then immediately injected in a straight microfluidic channel for observations. All experiments were performed with normal laboratory lighting and at room temperature. Cells retained normal motility throughout the experiments.
3.3.2 Hologram recording and de-noising
During the experiment, the cell suspension was driven into the micro-channel using a syringe pump by which the flow rates can be varied. The 3D motion of E. coli AW405 including cell swimming and flow advection in a sample volume of 400 × 400 × 200 μm3 were recorded with the DHM system (Fig. 1). The hologram plane is located at the plane 5 away from the bottom of the microfluidics inside bottom substrate. The experiments were conducted at flow rates of 0.05, 2.5, 25, and 100μl/min. In this paper primarily focusing on technique to visualize 3D bacterial motion, we only present the results at the flow rate of 2.5 μl/min (e.g. wall shear stress of 2.8 ). After recording, the background noise of individual hologram was removed by applying the algorithm outlined in §2.2.2. The appropriate cutoff length scale for the filter was 20 μm. The correlation coefficient matrix, , was computed in spatial domain directly. The ensemble averaging were performed at the critical coefficient threshold, . Note that the ensemble average is performed over original holograms instead of low pass filtered ones.
3.3.3 Reconstruction of 3D cell positions and tracking over time
The numerical reconstruction for each hologram was performed at equally spaced depths, 0.5μm (defined as reconstruction resolution in the depth direction), and range from z = 0 to 200μm from the bottom surface. The optical fields at these depths were numerically computed using the method [7]. The 2D images construct a 3D intensity field, from which 3D segmentation routine was used to identify the 3D profiles of each bacterium and subsequently extract its 3D position [1,7,39,40,51,64]. The in-focus image of each cell allowed us to determine its size, shape and cell orientation. With information, multi-criterion morphological filter was applied to remove non-bacterial particles. These morphology criteria include shape, size, aspect ratio and eccentricity [1,64]. Once cell position and morphological information are obtained, we track individual cell in 3D. The trajectories of the bacteria are formed, from which the motility is evaluated, e.g. swimming velocity, run and tumble characteristics, and linear and angular dispersion rate.
3.3.4 Computational expenses of de-noising algorithm and particle tracking procedure
It is noted that de-noising, numerical reconstruction, and particle tracking algorithms are computationally intensive. For example, a series of 20,000 holograms results in a correlation matrix of 20,000 × 20,000 coefficients totaling >3GBytes memory. Efficient implementation of the proposed de-noising algorithm on a single CPU with 16GB physical memory takes 120 hours. Such computation would be too prohibitive without effective parallelization. We have developed a parallel implementation that runs on a 16-node (256 CPUs) window-based High Performance Cluster (HPC), which reduces 120 hour computation to less than two hours. This parallel computing capability allows us to analyze the entire data set and produce the statistically robust background noise estimation for each individual hologram. Apart from de-noising, the numerical reconstruction and bacteria identification procedures are also very time consuming. Our parallel implementation of these algorithms takes 20 minutes per node to produce a single 3-D distribution of bacteria in suspension. In practices, it will take 16-node HPC cluster three weeks to process the entire series of holograms and produce hundreds of thousands of 3D bacterial trajectories. Briefly, parallel implementation of the proposed de-noising and trajectory retrieval algorithms makes the entire procedures feasible.
4. Results and discussion
In the following, we will demonstrate the efficacy of the proposed de-noising algorithm on bacterial DHM. The proposed de-noising method, for the first time, presents us a unique measurement capability in quantifying 3D bacterial motion within a dense suspension, while resolving the morphology of individual cell in motion with the resolutions of 0.2μm in lateral directions and 0.5μm in the depth direction. Figure 2 shows the comparative results of the proposed de-noising algorithm on bacterial and solid particle holograms as well as the results of the conventional de-noising algorithm. The left column of Fig. 2 shows the sample recording of bacteria, E. coli, and the corresponding de-noising results, while the right shows those of polystyrene particles with equivalent diameter. It is clear that at the high magnification, the background noise of the hologram is overwhelming and inhomogeneous. Although the fringes generated by particles are still observable in the original hologram [Fig. 2(d)], those interference fringes by bacteria, however, are completely unidentifiable in Fig. 2(a). For comparison purposes, both bacterial and particle holograms are processed with the conventional (Row 2 in Fig. 2) and the proposed de-noising (Row 3 in Fig. 2) procedures. The quality of bacterial hologram using conventional de-noising method [Eq. (5)] remains poor[Fig. 2(b)] in comparison to that of particle [Fig. 2(e)]. It supports our conclusion that when particle scattering is strong, the time-average de-noising method can be very effective. But as evident in Figs. 2(c) and 2(f) (e.g. holograms de-noised by the proposed method), the fringe contrasts in both bacterial and particle holograms have been greatly enhanced.
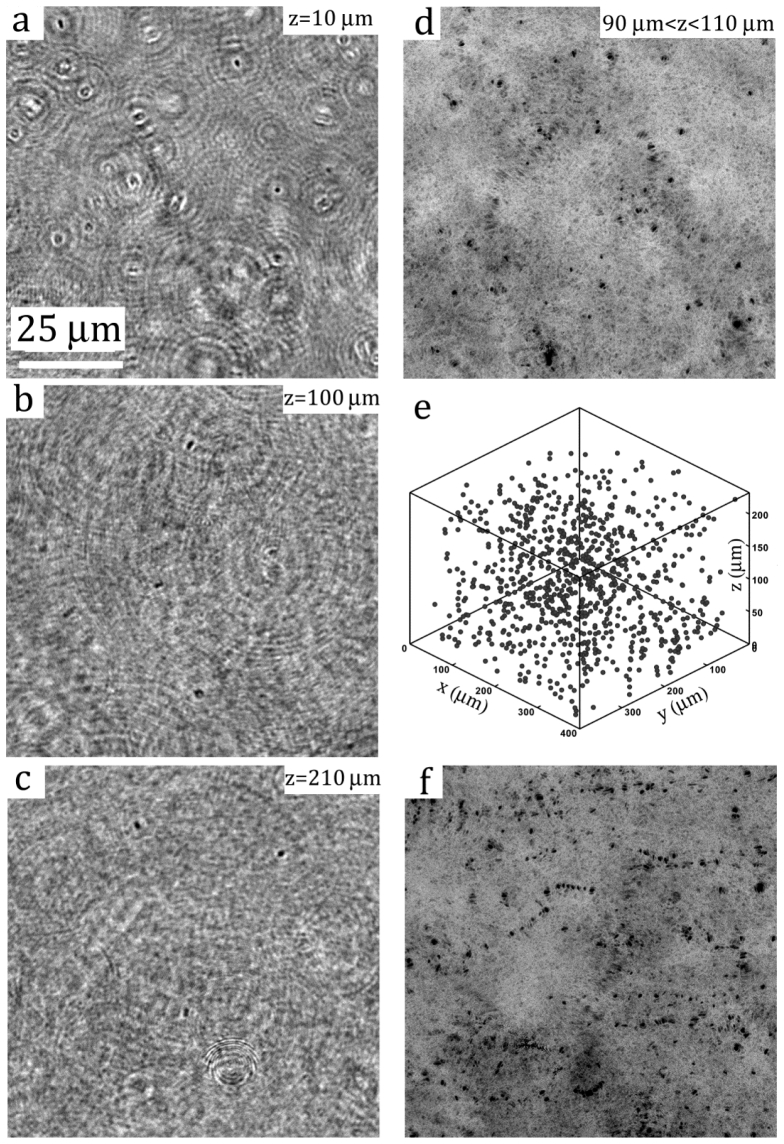
Figure 4 showcases several reconstructed images of a sample containing wild-type E. coli bacteria, AW405, at the concentration of A section (512 × 512 pixel or 100 × 100 μm2) section of a de-noised in-line hologram (2048 × 2048 pixels or 400 × 400 μm2), showing interference patterns generated by bacteria located at various depths, is presented in Fig. 2(c). Sample images reconstructed from the sample hologram [Fig. 2(c)] at three different depths are shown in Figs. 4(a)-4(c). The in-focus images of bacterial cells, appearing as dark elongated sphere in the bright background, along with dark concentric rings associated with close-by, out-of-focus particles, can be clearly observed. Close inspections indicate that the in-focus particle traces possess optical properties that are similar to those observed under a conventional microscope, i.e. a sharp dark edge with a bright spot in the middle. A combined/compressed image showing all the particles located within the depths, , is presented in Fig. 4(d). To bring all the particles in a volume into focus, we assign each pixel with the lowest intensity obtained over the depths, i.e. . The three dimensional distribution of all the particles within the reconstructed volume is presented in Fig. 4(e). To determine the 3-D coordinates of each particle we use a segmentation method developed in [7]. The segmentation procedure scans through the stacks of threshold images over depths and form a 3-D blob for each bacterium. The location of a bacterium center is then estimated using the centroid of the 3-D blob. In this example, the sample volume contains 893 identified E. coli, i.e. more than 30,000 cell/mm3. Superimposing combined images over five consecutive time instances (overall 1/3 s) within a 5 thick layer right above the bottom channel wall, we demonstrate the 2D projection of the swimming trajectory of each individual bacterium. Tracking these cells simultaneously over consecutive time, one is able to determine their 3D trajectories with high spatial resolutions.
Fig. 4.
Reconstructions of bacterial hologram shown in Fig. 2(c). (a-c) reconstructed images at 10, 100, and 210μm away from the hologram plane. (d) Superimposed reconstructions at the interval of 0.5μm of the sample volume from 90μm to 110μm away from the hologram plane. (e) 3D distribution of particles. (f) Superimposed images reconstructed at the depth varying from 10μm to 15μm at the interval of 0.5μm over 0.33s, totaling 5 time frames.
Clearly, the example (shown in Fig. 4) demonstrates adequately the efficacy of our de-noising algorithm in cleaning the background noise, enhancing the fringe contrast and later obtaining 3D bacterial distributions in a dense suspension over a substantial depth (> 100 cell body length). However, Sheng et al. [7] have shown that DHM inherits the shortcoming of in-line holography, namely the elongated depth-of-focus problem. This inherent problem greatly reduces one’s ability to determine the depth location of a particle. They also found that for the spherical particle DHM can resolve the depth location of a particle within 2~6 particle diameters ( ). The resolution increases up to ~1 with the increase of magnifications. Dueto the low scattering efficiency and non-spherical shape of bacteria, a few words on depth-of-focus and measurement uncertainty using the proposed de-noising algorithm are necessary. First, we present a stack of reconstructed images of an E. coli bacterium (Fig. 5 ) located at 37 away from the hologram plane. These images are reconstructed at depths varying from −7μm to 7μm at the pitch of 3.5μm based on its in-focus location. As the reconstruction moves closer to its in-focus location, the image of the bacterium becomes sharper and the shape of the cell becomes much better resolved. As the plane moves away from the centroid of the particle, the image becomes out of focus. In comparison, the microscopic images of E. coli at the magnification of 40X are captured at the corresponding distances (lower row in Fig. 5). We show qualitatively that bacterial DHM has reached the equivalent depth of field to the conventional microscopy and particle DHM. Close inspection at the in-focus image shows that the rod-like cell shape has been clearly obtained by DHM. In addition, the image contrast is in fact improved by using the proposed de-noising algorithm.
Fig. 5.

Numerically reconstructed images of a single E. coli cell recorded by DHM at the magnification of 40X with the range of at the interval of 3.5 . The center image, i.e. , is the in-focus image. The distance from the in-focus plane is marked on each sub image. The bottom row shows microscopic images of an E. coli at the corresponding planes from the in-focus location recorded by Nikon TiE with a Nikon Plan Fluor 40X objectives.
To quantify the depth-of-field, we measure the 3-D shape of the ensemble averaged bacterial cell using the ensemble-averaged distribution of
| (8) |
where is the position vector of the n-th particle’s centroid, represents a 3-D position with respect to the centroid of an ensemble-averaged bacterium cell, and subscript “max” refers to the maximum intensity within an averaging volume centered at each reconstructed bacterium. The ensemble volume has a dimension of or ( denoting the equivalent diameter of a rod-like E. coli cell), where the last term represents the depth direction, z. The distribution is ensemble over 100 cells randomly selected from 893 realizations. Figure 6(a) presents the iso-surface of intensity distribution (threshold at 0.8 of the peak value). Similar to DHM for solid particle [7], the reconstructed 3D bacterial cell is also elongated along the z axis with the smaller cross-section at the cell centroid. The one-dimensional intensity distribution along the depth direction is presented in Fig. 6(b). The intensity peaks when the cell is in focus and decreases away from the center. The width of the profile, defined based on 80% of its peak value, is 2.6μm (or ~2.08 ) and comparable to the result for a solid particle [7]. Differing to the intensity distribution of a solid particle, the asymmetry of the distribution is less pronounced and the amplitude of oscillations caused by the interference between scattering and reference light decays muchfaster. This observation is consistent with the intensity distribution associate with the Mie scattering by a particle having low scattering efficiency. The scattering characteristics has been accurately obtained by DHM. In short, the proposed de-noising algorithm has improved the quality of the bacterial hologram, and subsequently obtained accurate 3D information of bacterial cells while preserving high resolution details on every individual cell.
Fig. 6.
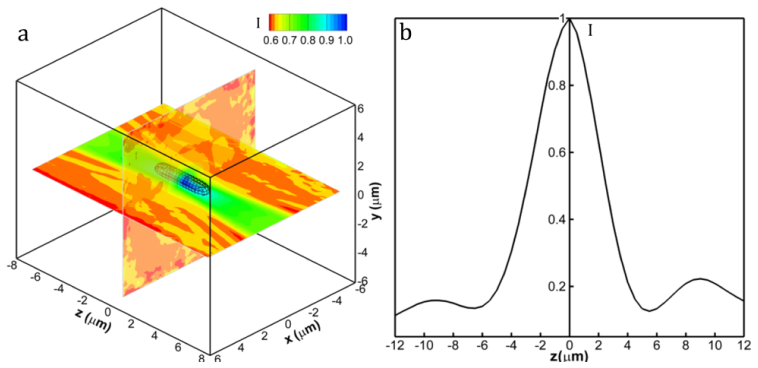
Intensity distribution of an ensemble averaged E. coli reconstruction. (a) Normalized 3D Intensity distribution of the ensemble averaged cell. Black lines show the iso-surface of intensity distribution threshold at 0.8. Two intersecting planes are x-y and x-z contour plots respectively. (b) The one-dimensional intensity distribution along the z axis. The width of the profile indicates the depth of focus of bacterial DHM.
Before concluding, we would like to demonstrate that digital holography microscopy with de-noising algorithm can be used for tracking thousands of bacteria in a dense suspension byrecording a sequence of hologram. Figure 7(a) shows the 3-D trajectory of a bacterium swimming in circles superimposed by the corresponding reconstructed in-focus images (every 5 images are shown for clarity). The result clearly demonstrates the capability of the proposed DHM method in capturing 3D locations of bacterial cell as an entire suspension as well as in resolving sub-micron scale kinematic information on each individual cell, such as the cell shape and orientation. It is able to quantify the bacterial motility events, such as swimming speed, tumbling and wobbling at the individual cell level with unprecedented spatial resolution, as well as the dynamics information, such as dispersion and interactions with mechanical and chemical environments, as a suspension, that are vital to understand key biological processes involved in biofilm formation and growth. Figure 7(b) presents a collection of swimming trajectories over one minute obtained within a sample volume of , the last being the depth. Totally 2973 trajectories are obtained. After automatic tracking, each trajectory is first verified manually against its superimposed 2D projection of in-focused images. Wrongly tracked trajectories are retraced based on multiple morphological criteria (details on tracking algorithm refer to supplemental information in ref [56]:). The DHM system in conjunction with the proposed de-noising method has been successfully applied to study the hydrodynamic interactions of swimming bacteria with a solid surface by Molaei et al. [1]. In that study [1], we have computed the swimming motility of E. coli bacterial trajectories, i.e. run and tumble, and compared them with Berg and Brown’s experiments conducted using a 3D tracking microscope [65]. The statistics of the run-and-tumble motility pattern in the bulk agree closely with theirs (summarized in Table 1 ). In particular, the mean swimming speed (14 µm/s) and the mean run time in the bulk (Tb = 0.93 s) differed by <1% and ~8%, respectively, from those of [65]. Key tumbling suppression mechanism that leads to cell trapping by the wall is discovered based on the results obtained by the DHM system in conjunction with the de-noising algorithm. The aforementioned study [1] has undoubtedly demonstrated the validity of trajectories and superb accuracy of the measurement when the proposed methods are applied to real life problems.
Fig. 7.
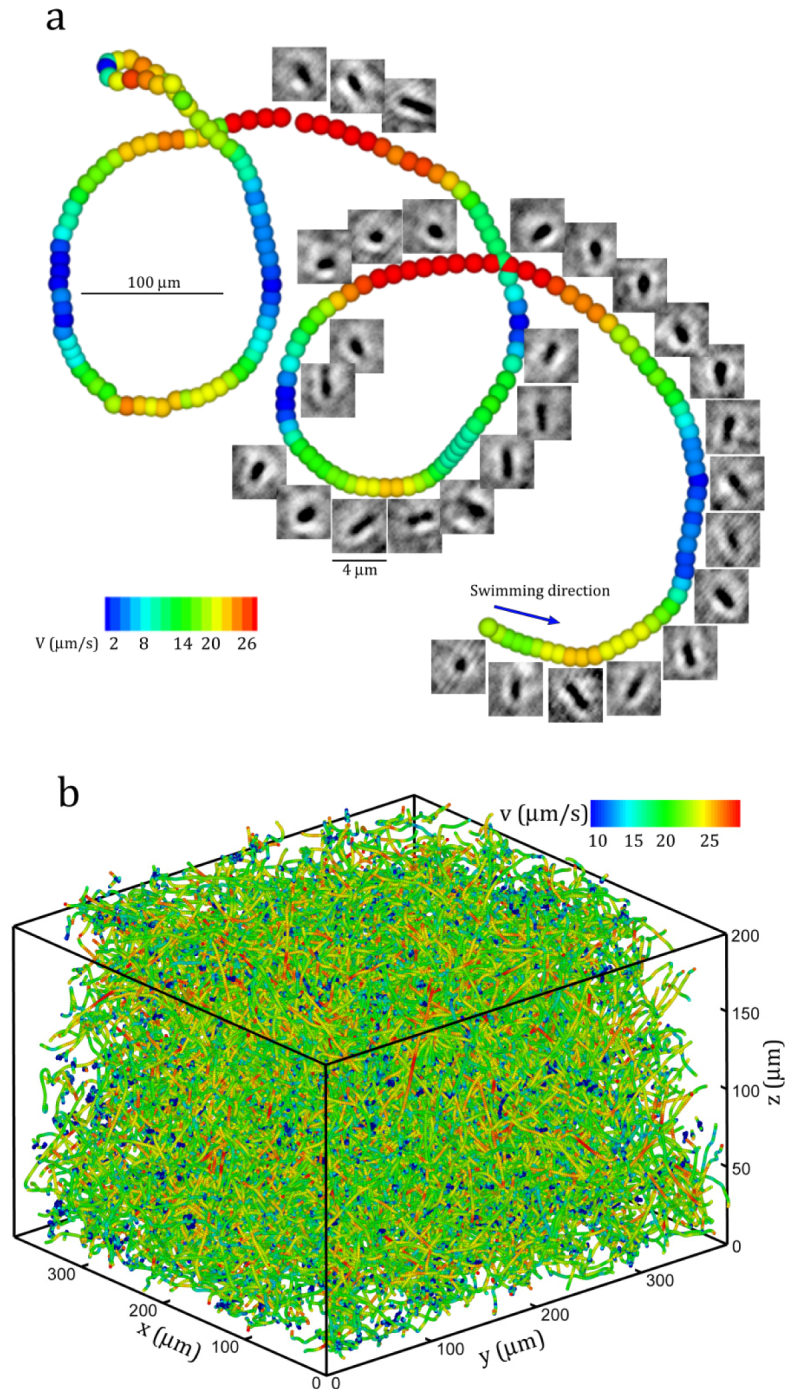
Sample 3D trajectories obtained by DHM: (a) A sample 3D trajectory showing a E. coli cell swimming in circle. The trajectory is superimposed by the corresponding reconstructed in-focus images. (b) Collection of 3D trajectories over one minute DHM recordings. Only half of the trajectories are shown. Color: the swimming speed.
Table 1. Motility characteristics of wild-type E. coli in the bulk compared to earlier results in the bulk [65]. The tumbling angle is the angle between two consecutive runs. Statistics were compiled over 2,750 trajectories, excluding cells immobilized on surfaces and represent mean ± standard deviation. (adopted and modified from ref [1].).
5. Conclusion
This paper introduces a novel de-noising algorithm to be used with in-line digital holographic microscopy to measure the spatial distribution of sub-micron (~1 ) bacterial cells in a dense aqueous suspension (~107 cells/ml) over the depth of 0.1~1mm (100~1000 ), and subsequently track these motile particles over time to reveal key biophysical processes involved in biofilm formation. Differing from particle holographic microscopy, imaging bacteria using DHM imposes substantial challenge due to the low scattering efficiency of bacterial cells, which is caused by the low contrast in refractive indices between cells and medium. To the best of our knowledge, there have been no existing methods that are capable of measuring spatial distributions of bacteria and subsequently tracking thousands of them simultaneously while preserving the morphological information of each individual cell.
Our analysis on noise characteristics of bacterial DHM has shown that the interferences of bacteria in each hologram are spatially localized and temporally incoherent, whereas thebackground noises due to the laser instability and interference of multiple reflections in the optical system are global and temporally coherent. This observation allows us to develop a correlation-based de-noising algorithm that identifies the background noise for each hologram in a series using correlation and constructs individual noise hologram using ensemble average among those correlated holograms. Once individual noise hologram is computed, a clean bacteria hologram is generated by subtracting the original hologram with the noise background. Although simple, the de-noising algorithm has shown exceptional capabilities of removing large scale background noise and enhancing the quality of bacterial hologram. The algorithm has been applied to the DHM recording of E. coli in microfluidics to study the hydrodynamic interactions of bacteria and their physical environments. We have demonstrated the effectiveness of the algorithm in improving the quality of holograms. This enhancement allows us to reconstruct 3D positions of bacterial cells in suspension and to recover submicron morphology and alignment of each individual cell. It has been shown that the de-noising algorithm permits DHM to maintain the spatial resolutions of 0.2μm in lateral and 0.5μm in the depth directions. The depth of focus reaches , equivalent to that for particle DHM. With a 40X objective, we have successfully de-noised DHM recording of E. coli bacteria suspension and reconstructed 3D cell positions with a submicron resolution in a dense suspension containing 107 cells/ml. Cinematographic DHM measurements demonstrate clearly that the proposed method is capable of tracking 3-D motion of bacteria and resolving cell morphological details simultaneously.
Acknowledgments
Research was supported in part by NSF under the grant no. CBET-1341901, NIH under the grant no. 1-R21-EB008844-01, and GoMRI (Gulf of Mexico Research Initiatives) under the grant no. SA12-03/GoMRI-003.
References and links
- 1.Molaei M., Barry M., Stocker R., Sheng J., “Failed Escape: Solid Surfaces Prevent Tumbling of Escherichia coli,” Phys. Rev. Lett. 113(6), 068103 (2014). 10.1103/PhysRevLett.113.068103 [DOI] [PubMed] [Google Scholar]
- 2.Drescher K., Dunkel J., Cisneros L. H., Ganguly S., Goldstein R. E., “Fluid dynamics and noise in bacterial cell-cell and cell-surface scattering,” Proc. Natl. Acad. Sci. U.S.A. 108(27), 10940–10945 (2011). 10.1073/pnas.1019079108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kantsler V., Dunkel J., Polin M., Goldstein R. E., “Ciliary contact interactions dominate surface scattering of swimming eukaryotes,” Proc. Natl. Acad. Sci. U.S.A. 110(4), 1187–1192 (2013). 10.1073/pnas.1210548110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lauga E., DiLuzio W. R., Whitesides G. M., Stone H. A., “Swimming in circles: Motion of bacteria near solid boundaries,” Biophys. J. 90(2), 400–412 (2006). 10.1529/biophysj.105.069401 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Marcos H. C., Fu H. C., Powers T. R., Stocker R., “Bacterial rheotaxis,” Proc. Natl. Acad. Sci. U.S.A. 109(13), 4780–4785 (2012). 10.1073/pnas.1120955109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Stocker R., “Reverse and flick: Hybrid locomotion in bacteria,” Proc. Natl. Acad. Sci. U.S.A. 108(7), 2635–2636 (2011). 10.1073/pnas.1019199108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sheng J., Malkiel E., Katz J., “Digital holographic microscope for measuring three-dimensional particle distributions and motions,” Appl. Opt. 45(16), 3893–3901 (2006). 10.1364/AO.45.003893 [DOI] [PubMed] [Google Scholar]
- 8.Greenberg G., Boyde A., “Novel method for stereo imaging in light-microscopy at high magnifications: reply,” Neuroimage 2, 86–87 (1995). 10.1006/nimg.1995.1011 [DOI] [PubMed] [Google Scholar]
- 9.Boyde A., “Stereoscopic images in confocal (tandem scanning) microscopy,” Science 230(4731), 1270–1272 (1985). 10.1126/science.4071051 [DOI] [PubMed] [Google Scholar]
- 10.Fan G. Y., Ellisman M. H., “Stereoscopy by tilted illumination in transmission electron microscopy,” Ultramicroscopy 55(2), 155–164 (1994). 10.1016/0304-3991(94)90166-X [DOI] [PubMed] [Google Scholar]
- 11.Bertilson M., von Hofsten O., Vogt U., Holmberg A., Hertz H. M., “High-resolution computed tomography with a compact soft x-ray microscope,” Opt. Express 17(13), 11057–11065 (2009). 10.1364/OE.17.011057 [DOI] [PubMed] [Google Scholar]
- 12.Gan L., Jensen G. J., “Electron tomography of cells,” Q. Rev. Biophys. 45(1), 27–56 (2012). 10.1017/S0033583511000102 [DOI] [PubMed] [Google Scholar]
- 13.Pawley J. B., Handbook of Biological Confocal Microscopy, 2nd ed. (Plenum Press, 233 Spring Street, New York, New York, USA London, England, UK, 2006). [Google Scholar]
- 14.Carlsson K., Aslund N., “Confocal imaging for 3-d digital microscopy,” Appl. Opt. 26(16), 3232–3238 (1987). 10.1364/AO.26.003232 [DOI] [PubMed] [Google Scholar]
- 15.McConnell G., “Confocal laser scanning fluorescence microscopy with a visible continuum source,” Opt. Express 12(13), 2844–2850 (2004). 10.1364/OPEX.12.002844 [DOI] [PubMed] [Google Scholar]
- 16.Xiao G. Q., Corle T. R., Kino G. S., “Real‐time confocal scanning optical microscope,” Appl. Phys. Lett. 53(8), 716–718 (1988). 10.1063/1.99814 [DOI] [Google Scholar]
- 17.Berg H. C., “How to track bacteria,” Rev. Sci. Instrum. 42(6), 868–871 (1971). 10.1063/1.1685246 [DOI] [PubMed] [Google Scholar]
- 18.Berg H. C., Brown D. A., “Chemotaxis in Escherichia coli analysed by three-dimensional tracking,” Nature 239(5374), 500–504 (1972). 10.1038/239500a0 [DOI] [PubMed] [Google Scholar]
- 19.Frymier P. D., Ford R. M., Berg H. C., Cummings P. T., “Three-dimensional tracking of motile bacteria near a solid planar surface,” Proc. Natl. Acad. Sci. U.S.A. 92(13), 6195–6199 (1995). 10.1073/pnas.92.13.6195 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Katz J., Sheng J., “Applications of holography in fluid mechanics and particle dynamics,” Annu. Rev. Fluid Mech. 42(1), 531–555 (2010). 10.1146/annurev-fluid-121108-145508 [DOI] [Google Scholar]
- 21.Xu W., Jericho M. H., Meinertzhagen I. A., Kreuzer H. J., “Digital in-line holography of microspheres,” Appl. Opt. 41(25), 5367–5375 (2002). 10.1364/AO.41.005367 [DOI] [PubMed] [Google Scholar]
- 22.Jericho S. K., Garcia-Sucerquia J., Xu W. B., Jericho M. H., Kreuzer H. J., “Submersible digital in-line holographic microscope,” Rev. Sci. Instr. 77, 043706 (2006). [Google Scholar]
- 23.Bishara W., Su T. W., Coskun A. F., Ozcan A., “Lensfree on-chip microscopy over a wide field-of-view using pixel super-resolution,” Opt. Express 18(11), 11181–11191 (2010). 10.1364/OE.18.011181 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Greenbaum A., Sikora U., Ozcan A., “Field-portable wide-field microscopy of dense samples using multi-height pixel super-resolution based lensfree imaging,” Lab Chip 12(7), 1242–1245 (2012). 10.1039/c2lc21072j [DOI] [PubMed] [Google Scholar]
- 25.Oh C., Isikman S. O., Khademhosseinieh B., Ozcan A., “On-chip differential interference contrast microscopy using lensless digital holography,” Opt. Express 18(5), 4717–4726 (2010). 10.1364/OE.18.004717 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Seo S., Isikman S. O., Sencan I., Mudanyali O., Su T. W., Bishara W., Erlinger A., Ozcan A., “High-throughput lens-free blood analysis on a chip,” Anal. Chem. 82(11), 4621–4627 (2010). 10.1021/ac1007915 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Su T. W., Erlinger A., Tseng D., Ozcan A., “Compact and light-weight automated semen analysis platform using lensfree on-chip microscopy,” Anal. Chem. 82(19), 8307–8312 (2010). 10.1021/ac101845q [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mudanyali O., Bishara W., Ozcan A., “Lensfree super-resolution holographic microscopy using wetting films on a chip,” Opt. Express 19(18), 17378–17389 (2011). 10.1364/OE.19.017378 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Carl D., Kemper B., Wernicke G., von Bally G., “Parameter-optimized digital holographic microscope for high-resolution living-cell analysis,” Appl. Opt. 43(36), 6536–6544 (2004). 10.1364/AO.43.006536 [DOI] [PubMed] [Google Scholar]
- 30.Colomb T., Dürr F., Cuche E., Marquet P., Limberger H. G., Salathé R. P., Depeursinge C., “Polarization microscopy by use of digital holography: application to optical-fiber birefringence measurements,” Appl. Opt. 44(21), 4461–4469 (2005). 10.1364/AO.44.004461 [DOI] [PubMed] [Google Scholar]
- 31.Dubois F., Minetti C., Monnom O., Yourassowsky C., Legros J. C., Kischel P., “Pattern recognition with a digital holographic microscope working in partially coherent illumination,” Appl. Opt. 41(20), 4108–4119 (2002). 10.1364/AO.41.004108 [DOI] [PubMed] [Google Scholar]
- 32.Dubois F., Yourassowsky C., Monnom O., Legros J.-C., Debeir O., Van Ham P., Kiss R., Decaestecker C., “Digital holographic microscopy for the three-dimensional dynamic analysis of in vitro cancer cell migration,” J. Biomed. Opt. 11(5), 054032 (2006). 10.1117/1.2357174 [DOI] [PubMed] [Google Scholar]
- 33.Kim M. K., Yu L. F., Mann C. J., “Interference techniques in digital holography,” J. Opt. A 8(7), S518–S523 (2006). 10.1088/1464-4258/8/7/S33 [DOI] [Google Scholar]
- 34.Rappaz B., Marquet P., Cuche E., Emery Y., Depeursinge C., Magistretti P. J., “Measurement of the integral refractive index and dynamic cell morphometry of living cells with digital holographic microscopy,” Opt. Express 13(23), 9361–9373 (2005). 10.1364/OPEX.13.009361 [DOI] [PubMed] [Google Scholar]
- 35.Awatsuji Y., Tahara T., Kaneko A., Koyama T., Nishio K., Ura S., Kubota T., Matoba O., “Parallel two-step phase-shifting digital holography,” Appl. Opt. 47(19), D183–D189 (2008). 10.1364/AO.47.00D183 [DOI] [PubMed] [Google Scholar]
- 36.Shaked N. T., Newpher T. M., Ehlers M. D., Wax A., “Parallel on-axis holographic phase microscopy of biological cells and unicellular microorganism dynamics,” Appl. Opt. 49(15), 2872–2878 (2010). 10.1364/AO.49.002872 [DOI] [PubMed] [Google Scholar]
- 37.Yamaguchi I., Zhang T., “Phase-shifting digital holography,” Opt. Lett. 22(16), 1268–1270 (1997). 10.1364/OL.22.001268 [DOI] [PubMed] [Google Scholar]
- 38.Zhang J., Xie Y., Li G. F., Ye Y. T., Saleh B. E. A., “Single-shot phase-shifting digital holography,” Opt. Eng. 53, 86884 (2014). [Google Scholar]
- 39.Chengala A., Hondzo M., Sheng J., “Microalga propels along vorticity direction in a shear flow,” Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 87(5), 052704 (2013). 10.1103/PhysRevE.87.052704 [DOI] [PubMed] [Google Scholar]
- 40.Sheng J., Malkiel E., Katz J., Adolf J. E., Place A. R., “A dinoflagellate exploits toxins to immobilize prey prior to ingestion,” Proc. Natl. Acad. Sci. U.S.A. 107(5), 2082–2087 (2010). 10.1073/pnas.0912254107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Gemmell B. J., Sheng J., Buskey E. J., “Morphology of seahorse head hydrodynamically aids in capture of evasive prey,” Nat. Commun. 4, 2840 (2013). [DOI] [PubMed] [Google Scholar]
- 42.Sheng J., Malkiel E., Katz J., “Single beam two-views holographic particle image velocimetry,” Appl. Opt. 42(2), 235–250 (2003). 10.1364/AO.42.000235 [DOI] [PubMed] [Google Scholar]
- 43.Danesh Panah M., Javidi B., “Tracking biological microorganisms in sequence of 3D holographic microscopy images,” Opt. Express 15, 10761–10766 (2007). 10.1364/OE.15.010761 [DOI] [PubMed] [Google Scholar]
- 44.Moon I., Daneshpanah M., Javidi B., Stern A., “Automated three-dimensional identification and tracking of micro/nanobiological organisms by computational holographic microscopy,” Proc. IEEE 97(6), 990–1010 (2009). 10.1109/JPROC.2009.2017563 [DOI] [Google Scholar]
- 45.Vater S. M., Weisse S., Maleschlijski S., Lotz C., Koschitzki F., Schwartz T., Obst U., Rosenhahn A., “Swimming behavior of Pseudomonas aeruginosa studied by holographic 3D tracking,” PLoS ONE 9(1), e87765 (2014). 10.1371/journal.pone.0087765 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Su T. W., Xue L., Ozcan A., “High-throughput lensfree 3D tracking of human sperms reveals rare statistics of helical trajectories,” Proc. Natl. Acad. Sci. U.S.A. 109(40), 16018–16022 (2012). 10.1073/pnas.1212506109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Otani M., Sato K., “Lens-less holographic microscopy with high resolving power for 4D measurement of microorganism swimming in water,” in Three-Dimensional and Multidimensional Microscopy: Image Acquisition and Processing Xix, Conchello J. A., Cogswell C. J., Wilson T., Brown T. G., eds. (Spie-Int Soc Optical Engineering, Bellingham, 2012). [Google Scholar]
- 48.Lewis N. I., Xu W. B., Jericho S. K., Kreuzer H. J., Jericho M. H., Cembella A. D., “Swimming speed of three species of Alexandrium (Dinophyceae) as determined by digital in-line holography,” Phycologia 45(1), 61–70 (2006). 10.2216/04-59.1 [DOI] [Google Scholar]
- 49.Kreuzer H. J., Jericho M. H., Meinertzhagen I. A., Xu W., “Digital in-line holography with numerical reconstruction: 4D tracking of microstructures and organisms,” in Practical Holography Xvii and Holographic Materials Ix, Jeong T. H., Stevenson S. H., eds. (Spie-Int Soc Optical Engineering, Bellingham, 2003), pp. 299–306. [Google Scholar]
- 50.Malkiel E., Sheng J., Katz J., Strickler J. R., “The three-dimensional flow field generated by a feeding calanoid copepod measured using digital holography,” J. Exp. Biol. 206(20), 3657–3666 (2003). 10.1242/jeb.00586 [DOI] [PubMed] [Google Scholar]
- 51.Sheng J., Malkiel E., Katz J., “Using digital holographic microscopy for simultaneous measurements of 3D near wall velocity and wall shear stress in a turbulent boundary layer,” Exp. Fluids 45(6), 1023–1035 (2008). 10.1007/s00348-008-0524-2 [DOI] [Google Scholar]
- 52.Talapatra S., Katz J., “Coherent structures in the inner part of a rough-wall channel flow resolved using holographic PIV,” J. Fluid Mech. 711, 161–170 (2012). 10.1017/jfm.2012.382 [DOI] [Google Scholar]
- 53.Talapatra S., Katz J., “Three-dimensional velocity measurements in a roughness sublayer using microscopic digital in-line holography and optical index matching,” Meas. Sci. Technol. 24(2), 024004 (2013). 10.1088/0957-0233/24/2/024004 [DOI] [Google Scholar]
- 54.Wyatt P. J., “Differential light scattering: a physical method for identifying living bacterial cells,” Appl. Opt. 7(10), 1879–1896 (1968). 10.1364/AO.7.001879 [DOI] [PubMed] [Google Scholar]
- 55.S. Talapatra, J. Sullivan, J. Katz, M. Twardowski, H. Czerski, P. Donaghay, J. R. Hong, J. Rines, M. McFarland, A. R. Nayak, and C. Zhang, “Application of in-situ digital holography in the study of particles, organisms and bubbles within their natural environment,” Ocean Sensing and Monitoring Iv 8372 (2012). [Google Scholar]
- 56.Sheng J., Malkiel E., Katz J., Adolf J., Belas R., Place A. R., “Digital holographic microscopy reveals prey-induced changes in swimming behavior of predatory dinoflagellates,” Proc. Natl. Acad. Sci. U.S.A. 104(44), 17512–17517 (2007). 10.1073/pnas.0704658104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Hansen A. T., Hondzo M., Sheng J., Sadowsky M. J., “Microscale measurements reveal contrasting effects of photosynthesis and epiphytes on frictional drag on the surfaces of filamentous algae,” Freshw. Biol. 59(2), 312–324 (2014). 10.1111/fwb.12266 [DOI] [Google Scholar]
- 58.Pu Y., Meng H., “Intrinsic aberrations due to Mie scattering in particle holography,” J. Opt. Soc. Am. A 20(10), 1920–1932 (2003). 10.1364/JOSAA.20.001920 [DOI] [PubMed] [Google Scholar]
- 59.Pu Y., Meng H., “Intrinsic speckle noise in off-axis particle holography,” J. Opt. Soc. Am. A 21(7), 1221–1230 (2004). 10.1364/JOSAA.21.001221 [DOI] [PubMed] [Google Scholar]
- 60.Tao B., Katz J., Meneveau C., “Geometry and scale relationships in high Reynolds number turbulence determined from three-dimensional holographic velocimetry,” Phys. Fluids 12(5), 941–944 (2000). 10.1063/1.870348 [DOI] [Google Scholar]
- 61.Zhang J., Tao B., Katz J., “Turbulent flow measurement in a square duct with hybrid holographic PIV,” Exp. Fluids 23(5), 373–381 (1997). 10.1007/s003480050124 [DOI] [Google Scholar]
- 62.Xia Y. N., Whitesides G. M., “Soft lithography,” Annu. Rev. Mater. Sci. 28(1), 153–184 (1998). 10.1146/annurev.matsci.28.1.153 [DOI] [Google Scholar]
- 63.Adler J., “A method for measuring chemotaxis and use of the method to determine optimum conditions for chemotaxis by Escherichia coli,” J. Gen. Microbiol. 74(1), 77–91 (1973). 10.1099/00221287-74-1-77 [DOI] [PubMed] [Google Scholar]
- 64.Sheng J., Malkiel E., Katz J., “Buffer layer structures associated with extreme wall stress events in a smooth wall turbulent boundary layer,” J. Fluid Mech. 633, 17–60 (2009). 10.1017/S0022112009006934 [DOI] [Google Scholar]
- 65.Berg H. C., Brown D. A., “Chemotaxis in Escherichia coli Analysed by Three-dimensional Tracking,” Nature 239(5374), 500–504 (1972). 10.1038/239500a0 [DOI] [PubMed] [Google Scholar]