Abstract
This paper considers conducting inference about the effect of a treatment (or exposure) on an outcome of interest. In the ideal setting where treatment is assigned randomly, under certain assumptions the treatment effect is identifiable from the observable data and inference is straightforward. However, in other settings such as observational studies or randomized trials with noncompliance, the treatment effect is no longer identifiable without relying on untestable assumptions. Nonetheless, the observable data often do provide some information about the effect of treatment, that is, the parameter of interest is partially identifiable. Two approaches are often employed in this setting: (i) bounds are derived for the treatment effect under minimal assumptions, or (ii) additional untestable assumptions are invoked that render the treatment effect identifiable and then sensitivity analysis is conducted to assess how inference about the treatment effect changes as the untestable assumptions are varied. Approaches (i) and (ii) are considered in various settings, including assessing principal strata effects, direct and indirect effects and effects of time-varying exposures. Methods for drawing formal inference about partially identified parameters are also discussed.
Key words and phrases: Causal inference, nonparametric bounds, partially identifiable models, sensitivity analysis
1. INTRODUCTION
In many areas of science, interest often lies in assessing the causal effect of a treatment (or exposure) on some particular outcome of interest. For example, researchers may be interested in estimating the difference between the average outcomes when all individuals are treated (exposed) versus when all individuals are not treated (unexposed). When treatment is assigned randomly and there is perfect compliance to treatment assignment, such treatment effects are identifiable and inference about the effect of treatment proceeds in a straightforward fashion. On the other hand, if the treatment assignment mechanism is not known to the analyst or compliance is not perfect, then these treatment effects are not identifiable from the observable data.
A statistical parameter is considered identifiable if different values of the parameter give rise to different probability distributions of the observable random variables. A parameter is partially identifiable if more than one value of the parameter gives rise to the same observed data law, but the set of such values is smaller than the parameter space. Traditionally, statistical inference has been restricted to the situation when parameters are identifiable. More recent research has considered methods for conducting inference about partially identifiable parameters. This research has been motivated to some extent by methods to evaluate causal effects of treatment, which are frequently partially identifiable. For instance, causal estimands are typically only partially identifiable in observational studies where the treatment selection mechanism is not known to the analyst. Noncompliance in randomized trials may also render treatment effects partially identifiable and a large amount of research has been devoted to drawing inference about treatment effects in the presence of noncompliance. Partial identifiability also arises when drawing inference about treatment effects within principal strata or effects describing relationships between an outcome and a treatment that are mediated by some intermediate variable.
In order to conduct inference about treatment effects that are partially identifiable, two approaches are often employed: (i) bounds are derived for the treatment effect under minimal assumptions, or (ii) additional untestable assumptions are invoked under which the treatment effect is identifiable and then sensitivity analysis is conducted to assess how inference about the treatment effect changes as the untestable assumptions are varied. Below (i) and (ii) are illustrated in five settings. In Section 2, we consider treatment effect bounds and sensitivity analysis when the treatment assignment mechanism is unknown. In Section 3, partial identifiability of principal strata causal effects are discussed. In Section 4, the setting of noncompliance is considered where there is interest in assessing the effect of treatment if there was perfect compliance. In Section 5, bounds and sensitivity analysis for direct and indirect effects in mediation analysis are presented, and in Section 6 longitudinal treatment effects are considered. Much of the literature on bounds and sensitivity analysis focuses on ignorance due to partial identifiability and tends to ignore uncertainty due to sampling error. Section 7 presents some methods that appropriately quantify this uncertainty when drawing inference about partially identifiable treatment effects. Section 8 concludes with a discussion.
2. TREATMENT SELECTION
2.1 Minimal Assumptions Bounds
Suppose we have a random sample of individuals where each potentially receives treatment or control. Unless otherwise indicated, let Z indicate treatment received where Z = 1 denotes treatment and Z = 0 denotes control. Denote the observed outcome of interest by Y. In order to define a treatment effect on the outcome Y, we first define potential outcomes for an individual when receiving treatment, denoted Y(1), and when receiving control, denoted Y(0). Throughout this paper, we invoke the stable unit treatment value assumption (SUTVA; Rubin, 1980), that is, there is no interference between units and there are no hidden (unrepresented) forms of treatment such that each individual has two potential outcomes {Y(0), Y(1)}. The no hidden forms of treatment guarantees that the observed outcome is equal to the potential outcome corresponding to the observed treatment, namely that Y = Y(z) for Z = z. Here, this will be referred to as causal consistency; for further discussion of causal consistency see Pearl (2010) and references therein. Once an individual receives treatment Z, the potential outcome Y(Z) is observed and the other potential outcome (or counterfactual) Y(1 − Z) becomes missing. Assume that n i.i.d. copies of (Z, Y) are observed and denoted by (Zi, Yi) for i = 1, …, n.
In this section, we consider treatment effect bounds when the treatment assignment mechanism is unknown. Here, Z can be thought of as treatment selection by the individual or by nature, rather than random treatment assignment as in an experiment. Define the average treatment effect ATE to be E[Y(1) − Y(0)] = E[Y(1)] − E[Y(0)] where E denotes the expected value. The ATE can be decomposed as
| (1) |
Note E[Y(z)|Z = z] = E[Y|Z = z] by causal consistency. Thus, from the observed data E[Y(z)|Z = z] and Pr[Z = z] are identifiable and can be consistently estimated by their empirical counterparts. On the other hand, the observed data provide no information about E[Y(z)|Z = 1 − z], such that (1) is only partially identifiable without additional assumptions.
Bounds on E[Y(1) − Y(0)] can be obtained by entertaining the smallest and largest possible values for E[Y(z)|Z = 1 − z]. If Y(1) and Y(0) are not bounded then bounds on E[Y(1) − Y(0)] will be completely uninformative, ranging from −∞ to ∞. Thus, informative bounds are only possible if Y(0) and Y(1) are bounded. Because any bounded variable can be rescaled to take values in the unit interval, without loss of generality assume Y(z) ∈ [0, 1] for z = 0, 1. Then 0 ≤ E[Y(z)|Z = 1 − z] ≤ 1 and from (1) it follows that E[Y(1) − Y(0)] is bounded below by setting E[Y(1)|Z = 0] = 0 and E[Y(0)|Z = 1] = 1, which yields the lower bound
| (2) |
Similarly, E[Y(1) − Y(0)] is bounded above by setting E[Y(1)|Z = 0] = 1 and E[Y(0)|Z = 1] = 0, which yields the upper bound
| (3) |
These bounds were derived independently by Robins (1989) and Manski (1990). The lower and upper bounds (2) and (3) are sharp in the sense that it is not possible to derive narrower bounds without additional assumptions. Note the interval formed by (2) and (3) is contained in [−1, 1] and is of width 1. Thus, the bounds are informative in that the treatment effect is now restricted to half of the otherwise possible range [−1, 1]. On the other hand, the bounds will always contain the null value 0 corresponding to no average treatment effect. That is, without additional assumptions the sign of the treatment effect cannot be determined from the observable data.
2.2 Additional Assumptions
The bounds (2)–(3) are sometimes called the “no assumptions” or “worst case” bounds because no assumptions are made about the effect of treatment in the population (Lee, 2005; Morgan and Winship, 2007). The only assumptions made in deriving (2) and (3) are SUTVA and that the observed data constitute a random sample. If additional assumptions are invoked, the treatment effect bounds may become tighter (i.e., narrower) or even collapse to a point (i.e., the treatment effect may become identifiable). Sometimes these additional assumptions will have implications that are testable based on the observed data. Should the observed data provide evidence against an assumption under consideration, then bounds should be computed without making this assumption.
An example of an additional assumption is mean independence, that is,
| (4) |
Under (4) ATE is identifiable. Specifically the upper and lower bounds for ATE both equal E[Y(1)|Z = 1] − E[Y(0)|Z = 0], which is identifiable from the observable data and can be consistently estimated by the “naive” estimator given by the difference in sample means between the groups of individuals receiving treatment and control. Assumption (4) will hold in experiments where treatment is randomly assigned as in a randomized clinical trial. Moreover, in randomized experiments the stronger assumption
| (5) |
will hold, where ∐ denotes independence. Independent treatment assignment (5) implies mean independence (4).
In some settings it may be reasonable to consider additional assumptions that are not as strong as (4) or (5) but nonetheless lead to tighter bounds than (2) and (3). For example, monotonicity type assumptions might be considered, such as monotone treatment selection (MTS)
| (6) |
MTS assumes individuals who select treatment will on average have outcomes greater than or equal to that of individuals who do not select treatment under the counterfactual scenario all individuals selected the same z. Manski and Pepper (2000) consider MTS when examining the effect of returning to school on wages later in life. For this example, MTS implies individuals who choose to return to school will have higher wages on average compared to individuals who choose to not return to school under the counterfactual scenario no individuals return to school. Alternatively, one might assume monotone treatment response (MTR)
(Manski, 1997). MTR assumes that under treatment each individual will have a response greater than or equal to that under control. For instance, suppose Z = 1 if an individual elects to get the annual influenza vaccine and Z = 0 otherwise, and let Y(z) = 1 if an individual subsequently does not develop flu-like symptoms when Z = z, and Y(z) = 0 otherwise. MTR asserts that each individual is more or as likely to not develop flu-like symptoms if they are vaccinated versus if they are unvaccinated. Given to date there is no evidence that the annual flu vaccine enhances the probability of acquiring influenza, MTR might be plausible for this example.
Assuming MTS or MTR can lead to narrower bounds than (2) and (3) because they imply additional constraints on unobserved counterfactual expectations. For example, assuming MTS, E[Y(0)|Z = 1] is bounded below by E[Y(0)|Z = 0] and E[Y(1)|Z = 0] is bounded above by E[Y(1)|Z = 1], implying the upper bound on E[Y(1) − Y(0)] is
| (7) |
for which the naive estimator is consistent. Under MTS, the lower bound remains (2). In contrast to the no assumptions bounds, assuming MTS the bounds may exclude 0, specifically when (7) is negative. MTR implies E[Y(1)] ≥ E[Y(0)] which in turn implies that the ATE lower bound is 0. Under MTR, the upper bound remains (3).
2.3 AZT Example
To illustrate the bounds above, consider a hypothetical study of 2000 HIV patients (from Figure 2 of Robins, 1989) where 1400 individuals elected to take the drug AZT and 600 elected not to take AZT (this is a simplified version of the problem Robins considers). The outcome of interest is death or survival at a given time point. Of the 2000 patients, 1000 died with exactly 500 from each group. Let Z = 1 if the patient elected to take AZT and Z = 0 otherwise; let Y = 1 if the individual died and 0 otherwise. The naive estimator, that is, the difference in sample means between Z = 1 and Z = 0, equals 500/1400 − 500/600 ≈ −0.48. The empirical estimates of the no assumptions bounds (2) and (3) equal −0.7 and 0.3. In this setting, the MTS assumption (6) supposes that individuals who elected to take AZT would have been more or as likely to die as individuals who did not take AZT in the counterfactual scenarios where everyone receives treatment or everyone does not receive treatment. This might be reasonable if it is thought that those who took AZT were on average less healthy than those who did not. Assuming MTS, the upper bound (7) is estimated to be −0.48. Thus, in this example the MTS bounds are substantially tighter than the no assumption bounds. The estimated MTS bounds lead to the conclusion (ignoring sampling variability, a point which we return to later) that AZT reduces the probability of death by at least 0.48 whereas without the MTS assumption we cannot even conclude whether the effect of treatment is nonzero.
2.4 Sensitivity Analysis
Assumptions such as (4) or (5) which identify the ATE, or assumptions such as MTS which sharpen the bounds, cannot be tested empirically because such assumptions pertain to the counterfactual distribution of Y(z) given Z = 1 − z. Robins and others (e.g., see Robins, Rotnitzky and Scharfstein, 2000; Scharfstein, Rotnitzky and Robins, 1999) have argued that a data analyst should conduct sensitivity analysis to explore how inference varies as a function of departures from any untestable assumptions.
For instance, a departure from assumption (5) might be due to the existence of an unmeasured variable U associated with both treatment selection Z and the potential outcomes Y(z) for z = 0, 1; a variable such as U is often referred to as an unmeasured confounder. Under this scenario, one might postulate that Y(z) ∐ Z|U for z = 0, 1 rather than (5). Sensitivity analysis proceeds by examining how inference drawn about ATE varies as a function of the magnitude of the association of U with Z, Y(0), and Y(1). This idea has roots as early as Cornfield et al. (1959), who demonstrated the plausibility of a causal effect of cigarette smoking (Z) on lung cancer (Y) by arguing that the absence of such a relationship was only possible if there existed an unmeasured factor U associated with cigarette use that was at least as strongly associated with lung cancer as cigarette use. This idea was further developed by Schlesselman (1978), Rosenbaum and Rubin (1983), Lin, Psaty and Kronmal (1998), Hernán and Robins (1999) and VanderWeele and Arah (2011) among others.
To illustrate this approach, suppose in the AZT example above that the analyst first assumes (5) holds, and thus estimates the effect of AZT to be −0.48. To proceed with sensitivity analysis, the analyst posits the existence of an unmeasured binary variable U and assumes that Y(z) ∐ Z|U for z = 0, 1. Similar to VanderWeele and Arah (2011), let
Then under the assumption that Y(z) ∐ Z|U for z = 0, 1, the naive estimator converges in probability to E[Y(1)] − E[Y(0)] + c(1) − c(0). Thus the naive estimator is asymptotically unbiased if and only if c(1) = c(0). For an alternative decomposition of the asymptotic bias of the naive estimator, see Morgan and Winship (2007, Section 2.6.3).
Sensitivity analysis proceeds by making varying assumptions about the unidentifiable associations of U with Y(0), Y(1) and Z. Under the most extreme of these assumptions, the bounds (2) and (3) are recovered. In particular, the upper bound in (3) is achieved when Pr[U = 1|Z = 1] = 0, Pr[U = 1|Z = 0] = 1, E[Y(1)|U = 1] = 1 and E[Y(0)|U = 0] = 0, meaning that the confounder U is perfectly negatively correlated with treatment Z and that if the confounder is present (U = 1), then a treated individual will die, whereas if the confounder is absent (U = 0), then an untreated individual will survive. The lower bound (2) is achieved under the opposite conditions.
In practice the extreme associations of U with Y(0), Y(1), and Z leading to the bounds might be considered unrealistic. Instead the analyst might consider associations only in a range deemed plausible by subject matter experts. In order to arrive at an accurate range, care should be taken in communicating the meaning of these associations and eliciting this range should be done in a manner that avoids data driven choices. Alternatively, the degree of associations required to change the sign of the effect of interest might be determined. For instance, suppose the analyst further assumes that E[Y(z)|U = 1] − E[Y(z)|U = 0] does not depend on z. This assumption will hold if the effect of Z on Y is the same if U = 0 or U = 1. Letting γ0 = E[Y(z)|U = 1] − E[Y(z)|U = 0] and γ1 = Pr[U = 1|Z = 1] − Pr[U = 1|Z = 0], the asymptotic bias of the naive estimator is then given by γ0γ1 and a bias adjusted estimator is found by subtracting γ0γ1 from the naive estimator. Sensitivity analysis may proceed by determining the values of γ0 and γ1 for which the bias adjusted estimator of the ATE will have the opposite sign of the naive estimator. For the AZT example, the bias adjusted estimator will have the opposite sign of the naive estimator if γ0γ1 < −0.48. This indicates that the product of (i) the difference in the mean potential outcomes between levels of the confounder for both treatment and control, and (ii) the difference in the prevalence of the unmeasured confounder between the treatment and control groups must be less than −0.48. Such magnitudes might be considered unlikely in the opinion of subject matter experts, in which case the sensitivity analysis would support the existence of a beneficial effect of AZT on survival among HIV+ men (ignoring sampling variability). Note the observed data distribution places some restrictions on the possible values of (γ0, γ1), that is, (γ0, γ1) is partially identifiable. For instance, if γ1 = 1 then Pr[U = 1|Z = 1] = 1 and Pr[U = 1|Z = 0] = 0 which implies E[Y(z)|U = u] = E[Y(z)|Z = u] and, therefore, max{E[Y(1)|Z = 1] − 1, −E[Y(0)|Z = 0]} ≤ γ0 ≤ min{E[Y(1)|Z = 1], 1 − E[Y(0)|Z = 0]}. Such considerations should be taken into account when determining the range of values of (γ0, γ1) in sensitivity analysis.
Because the data provide no evidence about U, VanderWeele (2008) and VanderWeele and Arah (2011) recommend choosing U and any simplifying assumptions based on what is considered plausible by relevant subject-matter experts. Such sensitivity analyses are most applicable when the existence of unmeasured confounders is known, but these factors could not be measured for logistical or other reasons. General bias formulas to be used for sensitivity analyses of unmeasured confounding for categorical or continuous outcomes, confounders and treatments can be found in VanderWeele and Arah (2011).
In other settings, there might not be any known unmeasured confounders, or it may be thought that there are numerous unmeasured confounders, in which cases the sensitivity analysis strategy described above would not be applicable or feasible. One general alternative approach entails making additional untestable assumptions regarding the unobserved potential outcome distributions. Typically, these assumptions (or models) are indexed by one or more sensitivity analysis parameters conditional upon which the causal estimand of interest is identifiable (e.g., Scharfstein, Rotnitzky and Robins, 1999; Brumback et al., 2004). Sensitivity analysis then proceeds by examining how inference changes as assumed values of the parameters are varied over plausible ranges. Examples of such sensitivity analyses are given below in Sections 3.4 and 6.3.
2.5 Covariate Adjustment
Typically in observational studies baseline (pretreatment) covariates X will be collected in addition to Z and Y. Incorporating information from observed covariates can help sharpen inferences about partially identified treatment effects. For example, incorporating covariates will generally lead to narrower bounds (Scharfstein, Rotnitzky and Robins, 1999). This follows because any treatment effect compatible with the distribution of observed variables (X, Y, Z) must also be compatible with the distribution of (Y, Z), that is, the observable variables if we do not observe or choose to ignore X (Lee, 2009). Covariate adjusted bounds are discussed further in Section 3.3 below.
Additionally, incorporating covariates may lend plausibility to some of the bounding assumptions discussed in Section 2.2. For example, in the absence of randomized treatment assignment (4) or (5) may be dubious. Instead of (4), it might be more plausible to assume
| (8) |
Similarly, assumption (5) might be replaced by
| (9) |
that is, each potential outcome is independent of treatment selection conditional on some set of covariates. Assumption (9) is commonly referred to as no unmeasured confounders. Assumptions such as (8) or weaker inequalities similar to (6) such as
may be deemed plausible for certain levels of X, but not for others. Availability of covariates also allows for the consideration of new types of assumptions (e.g., see Chiburis, 2010).
To conduct covariate adjusted sensitivity analysis, departures from identifying assumptions such as (9) can be explored. Similar to the previous section, a departure from (9) might entail positing the existence of an unmeasured variable U associated with both treatment selection Z and the potential outcomes Y(z) for z = 0, 1. Under this scenario, one might postulate that Y(z) ∐ Z|{X, U} for z = 0, 1 rather than (9) and sensitivity analysis proceeds by examining how inference varies as a function of the magnitude of the association of U with Z, Y(0), and Y(1) given X. Similar to covariate adjusted bounds, smaller associations or tighter regions of the values of the sensitivity parameters may be deemed plausible within certain levels of X, potentially yielding sharper inferences from the sensitivity analyses. However, as cautioned by Robins (2002), care should be taken in clearly communicating the meaning of such sensitivity parameters and their relationship to covariates when eliciting plausible ranges from subject matter experts. In some scenarios, plausible regions for sensitivity parameters may in fact be wider when conditioning on X than when not conditioning on X.
3. PRINCIPAL STRATIFICATION
3.1 Background
Even if treatment is randomly assigned (e.g., as in a clinical trial), the causal estimand of interest may still be only partially identifiable. For example, in many studies it is often of interest to draw inference about treatment effects on outcomes that only exist or are meaningful after the occurrence of some observable intermediate variable. For instance, in studies where some individuals die, investigators might be interested in treatment effects only among individuals alive at the end of the study. Unfortunately, estimands defined by contrasting mean outcomes under treatment and control that simply condition on this observable intermediate variable do not measure a causal effect of treatment without additional assumptions. One approach that may be employed in this scenario entails principal stratification (Frangakis and Rubin, 2002). Principal stratification uses the potential outcomes of the intermediate post-randomization variable to define strata of individuals. Because these “principal strata” are not affected by treatment assignment, treatment effect estimands defined within principal strata have a causal interpretation and do not suffer from the complications of standard post-randomization adjusted estimands. The simple framework of principal stratification has a wide range of applications. For a recent discussion of the utility (and lack thereof) of principal stratification, see Pearl (2011) and corresponding reader reactions.
As a motivating example for this section, we consider evaluating vaccine effects on post-infection outcomes. In vaccine studies, uninfected subjects are enrolled and followed for infection endpoints, and infected subjects are subsequently followed for postinfection outcomes such as disease severity or death due to infection with the pathogen targeted by the vaccine; often interest is in assessing the effect of vaccination on these post-infection endpoints (Hudgens and Halloran, 2006). For example, Préziosi and Halloran (2003) present data from a pertussis vaccine field study in Niakhar, Senegal. In this study, 3845 vaccinated children and 1020 unvaccinated children were followed for one year for pertussis. In the vaccine group, 548 children contracted pertussis, of whom 176 had severe infections; in the unvaccinated group 206 children contracted pertussis, of whom 129 had severe infections. In this setting, investigators are interested in assessing whether or not the vaccine had an effect on the severity of infection.
When assessing such post-infection effects, a data analyst might consider contrasts between study arms including all individuals under study, or, alternatively, only those who become infected. Though including all individuals in the study has the advantage of providing valid inference about the overall effect of vaccination (assuming independent treatment assignment), such an approach does not distinguish vaccine effects on susceptibility to infection from effects on the post-infection endpoint of interest. An analysis that conditions on infection attempts to distinguish these effects and may be more sensitive in detecting post-infection vaccine effects. However, because the set of individuals who would become infected under control are not likely to be the same as those who would become infected if given the vaccine, conditioning on infection might result in selection bias. For example, those who would become infected under vaccine may tend to have weaker immune systems than those who would become infected under control, and thus may be more susceptible to severe infection. Because of this potential selection bias, comparisons between infected vaccinees and infected controls do not necessarily have causal interpretations.
3.2 Principal Effects
In this section, treatment is vaccination, with Z = 1 corresponding to vaccination and Z = 0 corresponding to not being vaccinated. Assume that assignment to vaccine is equivalent to receipt of vaccine, that is, there is no noncompliance. Denote the potential infection outcome by S(z), where S(z) = 0 if uninfected and S(z) = 1 if infected. Here, the focus is on evaluating the causal effect of vaccine on Y, a post-infection outcome. For simplicity, we consider the case where Y is binary, indicating the presence of severe disease. If S(z) = 1, define the potential post-infection outcome Y(z) = 1 if the individual would have the worse (or more severe) post-infection outcome of interest given z, and Y(z) = 0 otherwise. If an individual’s potential infection outcome for treatment z is uninfected [i.e., S(z) = 0], then we adopt the convention that Y(z) is undefined. In other words, it does not make sense to define the severity of an infection in an individual who is not infected. This convention is similar to that employed in other settings. For instance, in the analysis of quality of life studies it might be assumed that quality of life metrics are not well defined in those who are not alive (Rubin, 2000).
Define a basic principal stratification P0 according to the joint potential infection outcomes SP0 = (S(0), S(1)). The four basic principal strata or response types are defined by the joint potential infection outcomes, (S(0), S(1)), and are composed of immune (not infected under both vaccine and placebo), harmed (infected under vaccine but not placebo), protected (infected under placebo but not vaccine), and doomed individuals (infected under both vaccine and placebo). Note the only stratum where both potential post-infection endpoints are well defined is in the doomed basic principal stratum, SP0 = (1, 1). Thus, defining a post-infection causal vaccine effect is only possible in the doomed principal stratum SP0 = (1, 1). Such a causal estimand will describe the effect of vaccination on disease severity in individuals who would become infected whether vaccinated or not. For instance, the vaccine effect on disease severity may be defined by
| (10) |
Frangakis and Rubin call treatment effect estimands such as (10) “principal effects.”
3.3 Bounds
Assume we observe n i.i.d. copies of (Z, S, Y) denoted by (Zi, Si, Yi) for i = 1, …, n. Also assume that the doomed principal strata is nonempty, Pr[SP0 = (1, 1)] > 0, so that the principal effect in (10) is well defined. Bounds for (10) are presented below under two additional assumptions: independent treatment assignment, that is,
| (11) |
and monotone treatment response with respect to S, that is,
| (12) |
Assumption (11) will hold in randomized vaccine trials. Monotonicity (12) assumes that the vaccine does no harm at the individual level, that is, there are no individuals who would be infected if vaccinated but uninfected if not vaccinated. Monotonicity is equivalent to assuming the harmed principal stratum is empty. Note no such monotonicity assumption is being made regarding Y. Under (11), assumption (12) implies P(S = 1|Z = 1) ≤ P(S = 1|Z = 0), which is testable using the observed data. For the pertussis example, the proportion infected in the vaccine group was less than in the unvaccinated group; thus, assuming (11), the data do not provide evidence against (12).
Assuming independent treatment assignment and monotonicity, (10) is partially identifiable from the observable data. The left term of (10) can be written
| (13) |
where the first equality holds under (12), the second equality under (11), and the third by causal consistency. On the other hand, the right term of (10) is only partially identifiable. To see this, note
| (14) |
In (14), only E[Y(0)|S(0) = 1] and Pr[S(1) = s|S(0) = 1] for s = 0, 1 are identifiable. In particular, E[Y(0)|S(0) = 1] = E[Y|S = 1, Z = 0] by similar reasoning to (13), and
where the first equality holds under (12) and the second under independent treatment assignment (and causal consistency). The other two terms in (14), namely E[Y(0)|SP0 = (1, 1)] and E[Y(0)|SP0 = (1, 0)], are only partially identifiable. In words, infected controls are a mixture of individuals in the protected and doomed principal stratum and without further assumptions the observed data do not identify exactly which infected controls are doomed. Therefore, the probability of severe disease when not vaccinated in the doomed principal stratum is not identified. Under (12), the data do however indicate what proportion of infected controls are doomed and this information provides partial identification of E[Y(0)|SP0 = (1, 1)], and hence (10).
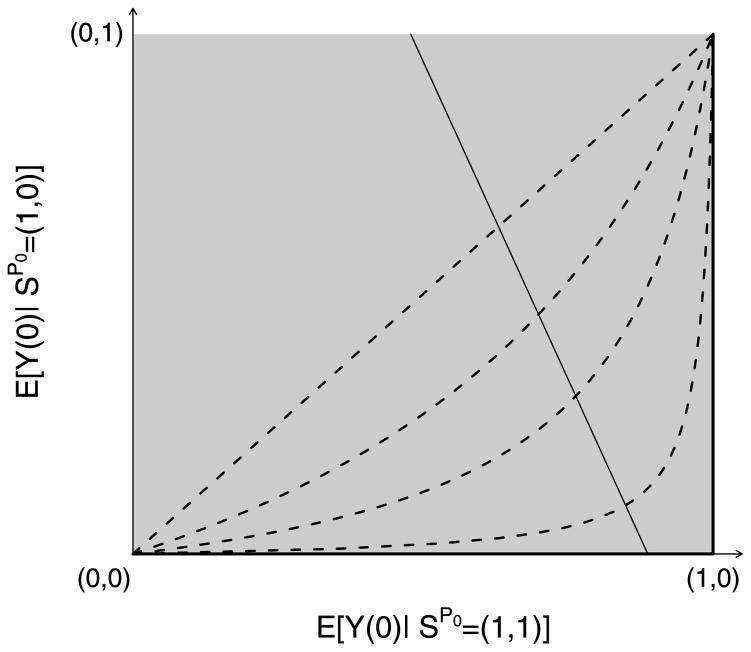
For fixed values of E[Y(0)|S(0) = 1] and Pr[S(1) = 1|S(0) = 1], any pair of expectations (E[Y(0)|SP0 = (1, 1)], E[Y(0)|SP0 = (1, 0)]) ∈ [0, 1]2 satisfying (14) will give rise to the same observed data distribution. Equation (14) describes a line segment with nonpositive slope intersecting the unit square as illustrated in Figure 1. An upper bound of E[Y(0)|SP0 = (1, 1)] and thus a lower bound for (10) is achieved when the line intersects the right or lower side of the square, that is, when either
Fig. 1.
Graphical depiction of the bounds and sensitivity analysis model described in Sections 3.3 and 3.4. The solid thin line with negative slope represents a set of joint distribution functions of (Z, S(1), S(0), Y(1), Y(0)) that all give rise to the same distribution of the observable random variables (Z, S, Y). The four dotted curves depict the log odds ratio selection model for γ = 0, 1, 2, 4. The γ = 0 model is equivalent to the no selection model. Each selection model identifies exactly one pair of expectations from this set, rendering the principal effect (10) identifiable. The thick black lines on the edge of the unit square correspond to the lower bound of the principal effect.
| (15) |
Together (14) and (15) imply E[Y(0)|SP0 = (1, 1)] is bounded above by
| (16) |
Similarly, E[Y(0)|SP0 = (1, 1)] is bounded below by
| (17) |
Combining (17) with (13) yields the upper bound on the principal effect of interest (10) and combining (16) with (13) yields the lower bound. These bounds were derived by Rotnitzky and Jemiai (2003), Zhang and Rubin (2003) and Hudgens, Hoering and Self (2003). Consistent estimates of (16) and (17) can be computed by replacing E[Y(0)|S(0) = 1] with ΣiYiI(Si = 1, Zi = 0)/ΣiI(Si = 1, Zi = 0) and Pr[S(1) = 1|S(0) = 1] with
Returning to the pertussis vaccine study, the estimated lower and upper bounds of (10) are −0.57 and −0.15. These estimated bounds exclude zero, leading to the conclusion (ignoring sampling variability) that vaccination lowers the risk of severe pertussis in individuals who will become infected regardless of whether they are vaccinated.
Note if Pr[S(1) = 1|S(0) = 1] = 1, that is, the vaccine has no protective effect against infection, then the protected principal stratum SP0 = (1, 0) is empty and both (16) and (17) equal E[Y(0)|S(0) = 1] meaning that (10) is identifiable and equals E[Y|Z = 1, S = 1] − E[Y|Z = 0, S = 1]. Intuitively, the lack of vaccine effect against infection eliminates the potential for selection bias.
As discussed in Section 2.5, incorporation of covariates can tighten bounds. For covariates X with finite support, one simple approach of adjusting for covariates entails determining bounds within strata defined by the levels of X and then taking a weighted average of the within strata bounds over the distribution of X. For the bounds in (16) and (17), adjustment for covariates will always lead to bounds that are at least as tight as bounds unadjusted for covariates (Lee, 2009; Long and Hudgens, 2013).
If the observed data provide evidence contrary to monotonicity (12), then bounds may be obtained under only (11). Without monotonicity (12), the proportion of infected controls that are in the doomed principal stratum is no longer identified but may be bounded in order to arrive at bounds for E[Y(0)|SP0 = (1, 1)]. In addition, the harmed principal stratum defined by SP0 = (0, 1) is no longer empty and thus E[Y(1)|SP0 = (1, 1)] is no longer identifiable from the observed data and may also be bounded in a similar fashion to E[Y(0)|SP0 = (1, 1)]. Details regarding these bounds without the monotonicity assumption may be found in Zhang and Rubin (2003) and Grilli and Mealli (2008).
3.4 Sensitivity Analysis
The bounds (16) and (17) are useful in bounding the vaccine effect on Y in the doomed stratum. However, these bounds may be rather extreme. An alternative approach is to make an untestable assumption that identifies the post-infection vaccine effect on Y and then consider how sensitive the resulting inference is to departures from this assumption. For instance, assuming
| (18) |
identifies (10). Hudgens and Halloran (2006) refer to this as the no selection model. To examine how inference varies according to departures from (18), following Scharfstein, Rotnitzky and Robins (1999), and Robins, Rotnitzky and Scharfstein (2000), consider the following sensitivity parameter:
| (19) |
In words, exp(γ) compares the odds of severe disease when not vaccinated in the doomed versus the protected principal stratum. Assuming (18) corresponds to γ = 0. A sensitivity analysis entails examining how inference about (10) varies as γ becomes farther from 0. For any fixed value of γ, (10) is identified (see Figure 1) and can be consistently estimated by maximum likelihood estimation without any additional assumptions (Gilbert, Bosch and Hudgens, 2003). The lower and upper bounds (17) and (16) are obtained by letting γ → ∞ and γ → −∞. To see this, note that as γ → ∞ (19) implies in the limit that either
which is equivalent to (15). Sensitivity analysis can be conducted by letting γ range over a set of values Γ.
Tighter bounds can be achieved by placing restrictions on Γ, perhaps based on prior beliefs about γ elicited from subject matter experts. For example, Shepherd, Gilbert and Mehrotra (2007) surveyed 10 recognized HIV experts in order to elicit a plausible range for a sensitivity parameter representing a departure from the assumption of no selection bias between vaccinated and unvaccinated individuals who acquired HIV during an HIV vaccine trial. Included in this survey was the analysis approach, a brief explanation of the potential for selection bias, the definition of the sensitivity parameter being employed, examples of the implications of certain sensitivity parameter values on selection bias and possible justification for believing certain values of the sensitivity parameter. The expert responses to the survey were fairly consistent and several written justifications for the respondents’ chosen ranges indicated a high level of understanding of both the counterfactual nature of the sensitivity parameter and the need to account for selection bias.
4. RANDOMIZED STUDIES WITH PARTIAL COMPLIANCE
4.1 Global Average Treatment Effect
In a placebo controlled randomized trial where (5) holds but there is non-compliance (i.e., individuals are randomly assigned to treatment or control but they do not necessarily adhere or comply with their assigned treatment), the naive estimator is a consistent estimator of the average effect of treatment assignment. However, in this case parameters other than the effect of treatment assignment may be of interest. As in the last section, a principal effect may be defined using compliance as the intermediate post-randomization variable over which to define principal strata; namely the principal strata would consist of individuals who would comply with their randomization assignment if assigned treatment or control or “compliers,” individuals who would always take treatment regardless of randomization or “always takers,” individuals who never take treatment “never takers” and individuals who take treatment only if assigned control or “defiers.” A principal effect of interest might be the effect of treatment in the complier principal stratum (Imbens and Angrist, 1994; Angrist, Imbens and Rubin, 1996), in which case bounds and sensitivity analyses similar to those in Section 3 are applicable. However, as several authors including Robins (1989) and Robins and Greenland (1996) have pointed out, such principal effects may not be of ultimate public health interest because they only apply to the subpopulation of compliers in clinical trials, which may differ from the population that elect to take treatment once licensed. For example, once efficacy is proved, a larger subpopulation of people may be willing to take the treatment. Effects defined on the subpopulation of compliers are also of limited decision-making utility because individual principal stratum membership is generally unknown prior to treatment assignment (Joffe, 2011).
Robins and Greenland (1996) suggested that in settings where the trial population could be persuaded to take the treatment once licensed, a more relevant public health estimand is the global average treatment effect, defined as the average effect of actually taking treatment versus not taking treatment given treatment assignment z. This causal estimand is similar to the average treatment effect defined in Section 2, but requires generalizing the potential outcome definitions used previously to include separate potential outcomes for each of the four combinations of treatment assignment and actual treatment received. For further discussion regarding causal models in presence of noncompliance, see Chickering and Pearl (1996) and Dawid (2003) among others.
Suppose we observe data from a clinical trial where each individual is randomly assigned to treatment or control. Let Z indicate treatment assignment where Z = 1 denotes treatment and Z = 0 denotes control. Suppose individuals do not necessarily comply with their randomization assignment and let S be a variable indicating whether or not treatment was actually taken, where S = 1 denotes treatment was taken and S = 0 otherwise. Thus, an individual is compliant with their randomization assignment if S = Z. Let Y be a binary outcome of interest. Denote the potential treatment taken by S(z) for z = 0, 1, where S(z) = 1 indicates taking treatment when assigned z and S(z) = 0 denotes not taking treatment when assigned z. Let Y(z, s) denote the potential outcome if an individual is assigned treatment z but actually takes treatment s. Conceiving of these potential outcomes depends on a supposition that trial participants who did not comply in the trial could be persuaded to take the treatment under other circumstances. Given this supposition, the global average treatment effect for each treatment assignment z = 1 and z = 0 is defined as GATEz = E[Y(z, 1) − Y(z, 0)]. For instance, GATE1 is the difference in the average outcomes under the counterfactual scenario everyone was assigned vaccine and did comply versus the counterfactual scenario everyone was assigned vaccine but did not comply.
Bounds for GATEz are given below under three assumptions: independent treatment assignment
| (20) |
monotonicity with respect to S
| (21) |
and the exclusion restriction
| (22) |
Assumption (22) indicates treatment assignment has no effect when the actual treatment taken is held fixed. Under (22), GATE0 = GATE1 which we denote by GATE. In this case each individual has two potential outcomes according to s = 0 and s = 1 [which could be denoted by Y(s) = Y(0, s) = Y(1, s) for s = 0, 1] and GATE is equivalent to the ATE discussed in Section 2 with z replaced by s. Robins (1989) derived bounds for GATE under several different combinations of (20)–(22) as well as some additional assumptions such as monotonicity with respect to S, that is, Y(z, 1) ≥ Y(z, 0) for z = 0, 1. Manski (1990) independently derived related results. Under (20)–(22), the sharp lower and upper bounds on GATE are
| (23) |
and
| (24) |
Balke and Pearl (1997) derived sharp bounds for GATE under a variety of assumptions, including (20)–(22), by recognizing that the derivation of the bounds is equivalent to a linear programming optimization problem. To see that bounds can be formulated as a linear programming optimization problem, first note that GATE can be expressed as a linear combination of probabilities of the joint distribution of L = (Y(0, 0), Y(0, 1), Y(1, 0), Y(1, 1), S(0), S(1))
| (25) |
where
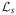 is the set of possible realizations of L where Y(0, s) = Y(1, s) = 1 for s = 0, 1. Under independent treatment assignment, there exists a linear transformation between the probabilities in the joint distribution of L and the probabilities in the conditional distribution of the observable random variables Y and S given Z, namely
is the set of possible realizations of L where Y(0, s) = Y(1, s) = 1 for s = 0, 1. Under independent treatment assignment, there exists a linear transformation between the probabilities in the joint distribution of L and the probabilities in the conditional distribution of the observable random variables Y and S given Z, namely
| (26) |
where
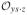 is the set of possible realizations of L where S(z) = s and Y(z, s) = y for z, y, s = 0, 1. To find the sharp bounds, the objective function (25) is minimized (or maximized) subject to the constraints (26), Pr[L = l] ≥ 0 for every l ∈
is the set of possible realizations of L where S(z) = s and Y(z, s) = y for z, y, s = 0, 1. To find the sharp bounds, the objective function (25) is minimized (or maximized) subject to the constraints (26), Pr[L = l] ≥ 0 for every l ∈
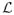 , and
, and
 Pr[L = l] = 1 where
Pr[L = l] = 1 where
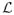 is the set of all possible realizations of L assuming (21) and (22). Optimization may be accomplished using the simplex algorithm and the dimension of this problem permits obtaining a closed form solution involving probabilities of the observed data distribution (Balke and Pearl, 1993), namely (23) and (24).
is the set of all possible realizations of L assuming (21) and (22). Optimization may be accomplished using the simplex algorithm and the dimension of this problem permits obtaining a closed form solution involving probabilities of the observed data distribution (Balke and Pearl, 1993), namely (23) and (24).
If in addition to assumptions (20) and (22), it is assumed that
| (27) |
for s, z = 0, 1 then GATE is identified and equals
| (28) |
(Hernán and Robins, 2006). For s = 0 assumption (27) is known as a no current treatment interaction assumption (Robins, 1994), and expression (28) is known as the instrumental variables estimand (Imbens and Angrist, 1994; Angrist, Imbens and Rubin, 1996). Sensitivity analyses may be conducted by defining sensitivity parameters representing departures from (20), (22) or (27) and then examining how inference about GATE varies as values of these parameters change. For instance, Robins, Rotnitzky and Scharfstein (2000) define current treatment interaction functions which represent a departure from (27) for s = 0.
4.2 Cholestyramine Example
To illustrate the GATE, we consider data presented in Pearl (2009, Section 8.2.6) on 337 subjects who participated in a randomized trial to assess the effect of cholestyramine on cholesterol reduction. Let Z = 1 denote assignment to cholestyramine and Z = 0 assignment to placebo. Let S = 1 if cholestyramine was actually taken by the participant and S = 0 otherwise. Let Y = 1 if the participant had a response and Y = 0 otherwise, where response is defined as reduction in the level of cholesterol by 28 units or more. Pearl reported the following observed proportions:
No participants assigned placebo actually took cholestyramine, suggesting the monotonicity assumption (21) is reasonable. On the other hand, 38.8% of individuals assigned treatment did not actually take cholestyramine.
From (23) and (24), the bounds on GATE assuming (21), (20) and (22) are estimated to be −1 + max{0.000, 0.473} + max{0.919, 0.315} = 0.392 and 1 − max{0, 0.139} − max{0.081, 0.073} = 0.780. The positive sign of the estimated bounds indicates the treatment is beneficial. Pearl interprets the estimated bounds as follows: “although 38.8% of the subjects deviated from their treatment protocol, the experimenter can categorically state that, when applied uniformly to the population, the treatment is guaranteed to increase by at least 39.2% the probability of reducing the level of cholesterol by 28 points or more.” Such an interpretation does not account for sampling variability, the topic of Section 7.
5. MEDIATION ANALYSIS
5.1 Natural Direct and Indirect Effects
As demonstrated in Sections 3 and 4, independent treatment assignment does not guarantee that the causal estimand of interest will be identifiable. Another setting where this occurs is in mediation analysis, where researchers are interested in whether or not the effect of a treatment is mediated by some intermediate variable. Even in studies where treatment is assigned randomly and there is perfect compliance, confounding may exist between the intermediate variable and the outcome of interest such that effects describing the mediated relationships will not in general be identifiable. Thus, bounds and sensitivity analysis may be helpful in drawing inference.
To illustrate, let Y be an observed binary outcome of interest, and S a binary intermediate variable observed some time between treatment assignment Z and the observation of Y. The goal is to assess whether and to what extent the effect of Z on Y is mediated by or through S. Denote the potential outcome of the intermediate variable under treatment z by S(z) for z = 0, 1 such that S = S(Z), and the potential outcomes under treatment z and intermediate s as Y(z, s) such that Y = Y(Z, S(Z)). Here, as in the previous section, it is assumed that both Z and S can be set to particular fixed values, such that there are four potential outcomes for Y per individual. Unless otherwise specified, independent treatment assignment (20) will be assumed throughout this section.
Define the total effect of treatment to be E[Y(1, S(1)) − Y(0, S(0))], which is equivalent to the ATE defined in Section 2.1. The total effect of treatment can be decomposed in the following way:
| (29) |
for z = 0,1 and z′ = 1 − z. The right-hand side of (29) decomposes the total effect into the sum of two separate effects. The first expectation on the right-hand side of (29) is the natural direct effect for treatment z, NDEz = E[Y(1, S(z)) − Y(0, S(z))] (Robins and Greenland, 1992; Pearl, 2001; Robins, 2003; Kaufman, Kaufman and MacLehose, 2009; Robins and Richardson, 2010). The natural direct effect is the average effect of the treatment on the outcome when the intermediate variable is set to the potential value that would occur under treatment assignment z. The second expectation on the right-hand side of (29) is the natural indirect effect, NIEz = E[Y(z, S(1)) − Y(z, S(0))] (Pearl, 2001; Robins, 2003; Imai, Keele and Yamamoto, 2010). The natural indirect effect is the difference in the average outcomes when treatment is set to z and the intermediate variable is set to the value that would have occurred under treatment compared to if the intermediate variable were set to the value that would have occurred under control.
Though the total effect is identifiable assuming (20), the natural direct and indirect effects are not identifiable since they entail E[Y(z, S(1 − z))] which depends on unobserved counterfactual distributions. Sjölander (2009) derived bounds for the natural direct effects assuming only independent treatment assignment (20) using the linear programming technique of Balke and Pearl (1997). This results in the following sharp lower and upper bounds for NDE0 and NDE1:
| (30) |
| (31) |
where pys·z = Pr(Y = y, S = s|Z = z). These bounds may exclude 0, indicating a natural direct effect of treatment z when the intermediate variable is set to S(z) (ignoring sampling variability). There are instances where the bounds in (30) and (31) may collapse to a single point, for example, if p10·0 = p10·1 = 1. Using (29), bounds for NIE0 and NIE1 can be obtained by subtracting the bounds for NDE1 and NDE0 from the total effect, which is identified under (20) and equal to (p11·1 + p10·1) − (p10·0 − p11·0).
Just as in Sections 2–4, monotonicity assumptions can be made to tighten the above bounds. For instance, if
are assumed, then Pr[L = l] = 0 for all l such that (i) S(0) = 1 and S(1) = 0, (ii) Y(0, s) = 1 and Y(1, s) = 0 for s = 0 or 1 or (iii) Y(z, 0) = 1 and Y(z, 1) = 0 for s = 0 or 1, which restricts the feasible region of the linear programming problem. The resulting sharp bounds for the natural direct effect are
| (32) |
(Sjölander, 2009). The bounds (32) are always at least as narrow as (30) and (31). Interestingly these narrower bounds do not depend on z. The bounds in (32) may also collapse to a single point, for example, if p10·0 = p10·1 and p01·0 − p01·1 = p11·1 − p11·0.
The natural direct effect provides insight into whether or not treatment yields additional benefit on the outcome of interest when the influence of treatment on the intermediate variable is eliminated. However, researchers might also be interested in what benefit is provided by treatment if the effect of the intermediate variable on the outcome is eliminated or held constant. This question suggests a different causal estimand known as the controlled direct effect. Bounds for the controlled direct effect can be found in Pearl (2001), Cai et al. (2008), Sjölander (2009) and VanderWeele (2011a).
5.2 Sensitivity Analysis
As in other settings where the effect of interest is not identifiable, sensitivity analysis in the mediation setting may be conducted by making untestable assumptions that identify the direct or indirect effects. Then sensitivity of inference to departures from these assumptions can be examined. For example, if (20) holds, then the natural direct and indirect effects are identified under the following additional assumptions
| (33) |
| (34) |
(Pearl, 2001; VanderWeele, 2010). Assumption (33) would be valid if subjects were randomly assigned S within different levels of treatment assignment Z. In settings where S is not randomly assigned, (33) might be considered plausible if it is believed that conditional on Z there are no variables which confound the mediator–outcome relationship. Both assumptions (33) and (34) will not hold in general if Z has an effect on some other intermediate variable, say R, which in turn has an effect on both S and Y. Thus, (33) and (34) may fail unless the mediator S occurs shortly after treatment Z. Under assumptions (20), (33) and (34),
and
Because assumptions (33) and (34) cannot be empirically tested, sensitivity analysis should be conducted. Similar to Section 2.4, sensitivity analysis might proceed by positing the existence of an unmeasured confounding variable U associated with the potential mediator values S(z) and the potential outcomes Y(z, s) for z, s = 0, 1. Assumption (33) would then replaced by Y(z, s) ∐ S|{Z, U} and (34) by Y(z, s) ∐ S(z′)|U for s, z, z′ = 0, 1. Sensitivity analysis would then proceed by exploring how inference about the natural direct and indirect effects changes as the magnitude of the associations of U with S(z) and Y(s, z′) for z, z′, s = 0, 1 vary. For further details regarding bounds and sensitivity analysis in mediation analysis, see Imai, Keele and Yamamoto (2010), VanderWeele (2010) and Hafeman (2011).
6. LONGITUDINAL TREATMENT
6.1 Background
In Sections 2–5, treatment is assumed to remain fixed across follow up time and outcomes are one-dimensional. However, frequently researchers are interested in assessing causal effects comparing longitudinal outcomes for patients on different treatment regimens where treatment may vary in time. As the number of times at which an individual may receive treatment increases, the number of possible treatment regimens increases exponentially. Because each treatment regimen corresponds to a separate potential (longitudinal) outcome and only one potential outcome is ever observed, the fraction of potential outcomes that are unobserved quickly grows close to one as the number of possible treatment times increases. As in other settings, unless treatment regimens are randomly assigned, regimen effects will not be identifiable without additional assumptions. In the longitudinal setting, bounds will typically be largely uninformative because of the high proportion of unobserved potential outcomes. Therefore, analyses usually proceed by invoking modeling assumptions that render treatment effects identifiable and then conducting sensitivity analysis corresponding to key untestable modeling assumptions.
Models for potential outcomes as functions of covariates (such as treatment) and possibly other potential outcomes are often referred to as structural models. For longitudinal potential outcomes and treatments, popular models include structural nested models and marginal structural models (Robins, Rotnitzky and Scharfstein, 2000; Robins, 1999; van der Laan and Robins, 2003; Brumback et al., 2004). In Section 6.2 below, we consider a marginal structural model where the treatment effect is identified assuming conditionally independent treatment assignment. Sensitivity analyses exploring departures from this assumption are then considered in Section 6.3.
6.2 Marginal Structural Model
Consider a study where individuals possibly receive treatment at τ fixed time points (i.e., study visits). In general let Ā(t) = (A(0), …, A(t)) represent the history of variable A up to time t and Ā be the entire history of variable A such that Ā = Ā(τ). Let z(t) = 1 indicate treatment at visit t, and z(t) = 0 otherwise such that z̄ represents a treatment regimen for visits 0, …, τ. Denote the observed treatment regimen up to time t as Z̄(t). Let Y be some outcome of interest that may be categorical or continuous, and denote the potential outcome of Y at visit t for regimen z̄ by Y(z̄, t) and the observed outcome by Y(t). Let X̄(t) denote the history of some set of time varying covariates up to time t, where X(0) denotes the baseline covariates. Assume for simplicity there is no loss to follow-up or noncompliance such that we observe n i.i.d. copies of (Z̄, Ȳ, X̄).
Consider the following marginal structural model of the mean potential outcome were the entire population to follow regimen z̄ up to time t:
| (35) |
for t ∈ {1, …, τ}, where and g(·) is an appropriate link function. The causal estimand of interest is β1, the regression coefficient for cum[z̄(t − 1)], which is the effect of having received treatment at one additional visit prior to time t conditional on baseline covariates X(0). Because (35) involves counterfactual outcome distributions, β1 is not identifiable without additional assumptions. One additional assumption is conditionally independent treatment assignment
| (36) |
(Robins, Rotnitzky and Scharfstein, 2000; Robins, 1999; Brumback et al., 2004). This assumption is true if the potential outcome at visit t under treatment regimen z̄ is independent of the observed treatment at visit k given the history of treatment up to visit k − 1 and the covariate history up to visit k. Assuming both a correctly specified model (35) and conditionally independent treatment assignment (36), fitting the following model to the observed data:
using generalized estimating equations with an independent working correlation matrix and time varying inverse probability of treatment weights (IPTW) yields an estimator η̂1 that is consistent for β1 (Tchetgen Tchetgen et al., 2012a, 2012b).
6.3 Sensitivity Analysis
If assumption (36) does not hold, then the IPTW estimator η̂1 is not necessarily consistent. Because (36) is not testable from the observed data, sensitivity analysis might be considered to assess robustness of inference to departures from (36). Following Robins (1999) and Brumback et al. (2004), let
for t > k and z̄ such that Pr[Z(k) = z(k)|Z̄(k − 1) = z̄(k − 1)] is bounded away from 0 and 1. The function c quantifies departures from the conditional independent treatment assignment assumption (36) at each visit t > k, where c(t, k, z̄(t − 1), x̄(k)) = 0 for all z̄ and t > k if (36) holds. For the identity link, a bias adjusted estimator of the causal effect β1 may be obtained by recalculating the IPTW estimator with the observed outcome Y(t) replaced by Yγ(t) = Y(t) − b(Z̄(t − 1), X̄(t − 1)) where
and f[z(k)|z̄(k − 1), x̄(k)] = P̂r[Z(k) = z(k)|Z̄(k − 1) = z̄(k − 1), X̄(k) = x̄(k)] is an estimate of the conditional probability of the observed treatment based on some fitted parametric model (Brumback et al., 2004). Provided this parametric model and c are both correctly specified, this bias adjusted estimator, say η̃1, is consistent for β1. Sensitivity analysis proceeds by examining how η̃1 changes when varying sensitivity parameters in c(t, k, z̄(t − 1), x̄(k)).
Because c(t, k, z̄(t − 1), x̄(k)) is not identifiable from the observable data, Robins (1999) recommends choosing a particular c that is easily explainable to subject matter experts to facilitate eliciting plausible ranges of the sensitivity parameters. As an example of a particular c, Brumback et al. (2004) suggest c(t, k, z̄(t − 1), x̄(k)) = γ{2z(k) − 1} where γ is an unidentifiable sensitivity analysis parameter. Note that c(t, k, z̄(t − 1), x̄(k)) = γ for z(k) = 1 and c(t, k, z̄(t − 1), x̄(k)) = −γ for z(k) = 0. Thus, γ > 0 (γ < 0) corresponds to subjects receiving treatment at time k having greater (smaller) mean potential outcomes at future visit t than those who did not receive treatment at visit k. When γ = 0, Y(t) = Yγ(t) and therefore η̃1 = η̂1. The function c might depend on the baseline covariates X(0) or the time-varying covariates X̄(k). In this case, as in Section 2.5, care should be taken in clearly communicating the sensitivity parameters’ relationship to these covariates when eliciting plausible ranges from subject matter experts. Another consideration when choosing a function c is whether it will allow for the sharp null of no treatment effect, that is, for all individuals Y(z̄, t) = Y(z̄′, t) for all z̄, z̄′, t. The example function c presented above allows for the sharp null. See Brumback et al. (2004) for other example c functions and further discussion of sensitivity analysis for marginal structural models.
7. IGNORANCE AND UNCERTAINTY REGIONS
Treatment effect bounds describe ignorance due to partial identifiability but do not account for uncertainty due to sampling error. This section discusses some methods to appropriately quantify uncertainty due to sampling variability when drawing inference about partially identifiable treatment effects. Over the past decade, a growing body of research, especially in econometrics, has considered inference of partially identifiable parameters. The approach presented below draws largely upon Vansteelandt et al. (2006), who considered methods for quantifying uncertainty in the general setting where missing data causes partial identifiability. As questions about treatment (or causal) effects can be viewed as missing data problems, the approach of Vansteelandt et al. generally applies (under certain assumptions) to the type of problems considered throughout this paper. This approach builds on earlier work by Robins (1997) and others.
7.1 Ignorance Regions
Let L be a vector containing the potential outcomes for an individual, let O denote the observed data vector, and let R be a vector containing indicator variables denoting whether the corresponding component of L is observed. For example, L = (Y(1), Y(0)), O = (Z, Y), and R = (Z, (1 − Z)) for the scenario described in Section 2 and L = (Y(1), Y(0), S(1), S(0)), O = (Z, Y, S) and R = (Z, (1 − Z), Z, (1 − Z)) for the scenario described in Section 3. Denote the distribution of (L, R) by f(L, R) and let f(L) = ∫ f(L, R)dR. The goal is to draw inference about a parameter vector β which is a functional of the distribution of potential outcomes L; this is sometimes made explicit by writing β = β{f(L)}. Denote the true distribution of (L, R) by f0(L, R) and the true value of β by β0 = β{f0(L)}. For example, β0 = E[Y(1) − Y(0)] for the scenario described in Section 2 and β0 = E[Y(1) − Y(0)|SP0 = (1, 1)] for the scenario described in Section 3. Denote the true observed data distribution by f0(O) = ∫ f0(L, R) dL(1 − R) where L(1 − r) denotes the missing part of L when R = r (i.e., the unobserved potential outcomes). The challenge in drawing inference about β0 is that there may be multiple full data distributions f(L, R) that marginalize to the true observed data distribution, that is, f0(O) = ∫ f(L, R)dL(1 − R) for some f ≠ f0. When this occurs, β may be only partially identifiable from O, in which case bounds can be derived for β0 as illustrated in the sections above.
The set of values of β{f(L)} such that f(L, R) marginalizes to the true observed data distribution is sometimes called the ignorance region or the identified set. These ignorance regions or intervals are distinct from traditional confidence intervals in that as the sample size tends to infinity these intervals will not shrink to a single point when β is partially identifiable. The ignorance region for β can be defined formally as follows. Following Robins (1997), define a class
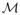 (γ) of full data laws indexed by some sensitivity parameter vector γ to be nonparametrically identified if for each observed data law f(O) there exists a unique law f(L, R; γ) ∈
(γ) of full data laws indexed by some sensitivity parameter vector γ to be nonparametrically identified if for each observed data law f(O) there exists a unique law f(L, R; γ) ∈
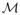 (γ) such that f(O) = ∫ f(L, R; γ)dL(1 −
R). In other words, the class
(γ) such that f(O) = ∫ f(L, R; γ)dL(1 −
R). In other words, the class
 (γ) contains a unique distribution that marginalizes to each possible observed data distribution. For example, for the sensitivity analysis approach in Section 3.4, Hudgens and Halloran (2006, §4.3.3) defined a class of full data laws indexed by γ given in (19) that is nonparametrically identified. The ignorance region for β is formally defined to be
(γ) contains a unique distribution that marginalizes to each possible observed data distribution. For example, for the sensitivity analysis approach in Section 3.4, Hudgens and Halloran (2006, §4.3.3) defined a class of full data laws indexed by γ given in (19) that is nonparametrically identified. The ignorance region for β is formally defined to be
| (37) |
where Γ is the set of all possible values of γ under whatever set of assumptions is being invoked and
 (Γ) = ⋃γ
∈ Γ
(Γ) = ⋃γ
∈ Γ
 (γ). Assume
(γ). Assume
 (Γ) contains the true full data distribution, that is, f0(L, R) = f(L, R, γ0) for some γ0 ∈ Γ. [For considerations when
(Γ) contains the true full data distribution, that is, f0(L, R) = f(L, R, γ0) for some γ0 ∈ Γ. [For considerations when
 (Γ) does not contain the true full data distribution, see Todem, Fine and Peng (2010).] Because
(Γ) does not contain the true full data distribution, see Todem, Fine and Peng (2010).] Because
 (γ) is nonparametrically identified, for each γ ∈ Γ there is a single β(γ) = β{∫ f(L, R; γ)dR)} in the ignorance region (37). If
(γ) is nonparametrically identified, for each γ ∈ Γ there is a single β(γ) = β{∫ f(L, R; γ)dR)} in the ignorance region (37). If
 (Γ) includes all possible full data distributions that marginalize to any possible observed data distribution, then the ignorance region will contain the bounds.
(Γ) includes all possible full data distributions that marginalize to any possible observed data distribution, then the ignorance region will contain the bounds.
In practice, the ignorance region will be unknown because it depends on the unknown true observed data distribution f0(O). For γ fixed, β(γ) is identifiable from the observed data and the ignorance region can be estimated by estimating β(γ) for each value of γ ∈ Γ, denoted by β̂(γ). The resulting estimator of irf0(β, Γ) is then {β̂(γ) : γ ∈ Γ}. For scalar β(γ), let β̂l = infγ ∈ Γ{β̂(γ)} and β̂u = supγ ∈ Γ{β̂(γ)} such that the estimated ignorance region is contained in the interval [β̂l, β̂u].
7.2 Uncertainty Regions
Estimated ignorance regions convey ignorance due to partial identifiability and do not reflect sampling variability in the estimates. Indeed much of the literature on bounds and sensitivity analysis of treatment effects tends to report estimated ignorance regions and either ignores sampling variability or employs ad-hoc inferential approaches such as pointwise confidence intervals conditional on each value of the unidentifiable sensitivity parameter. More recent developments have provided a formal framework for conducting inference in partial identifiability settings (Imbens and Manski, 2004; Vansteelandt et al., 2006; Romano and Shaikh, 2008; Bugni, 2010; Todem, Fine and Peng, 2010). The main focus in this research has been the construction of confidence regions for either the parameter β0 or the ignorance region irf0(β0, Γ).
Following Vansteelandt et al. (2006), a (1 − α) pointwise uncertainty region for β0 is defined to be a region URp(β, Γ) such that
where Prf0 {·} denotes probability under f0(O). That is, URp(β, Γ) contains β(γ) with at least probability 1 − α for all γ ∈ Γ. In particular, assuming γ0 ∈ Γ, then URp(β, Γ) will contain β0 = β(γ0) with at least probability 1 − α.
An appealing aspect of pointwise uncertainty regions is that they retain the usual duality between confidence intervals and hypothesis testing. Namely, one can test the null hypothesis H0 : β0 = βc versus Ha : β0 ≠ βc for some specific βc at the α significance level by rejecting H0 when the (1 − α) pointwise uncertainty region URp(β, Γ) excludes βc. This is easily shown by noting for βc = β(γ0)
where the last inequality follows because URp(β, Γ) is a (1 − α) pointwise uncertainty region.
Various methods under different assumptions have been proposed for constructing pointwise uncertainty regions. Imbens and Manski (2004) and Vansteelandt et al. (2006) proposed a simple method for constructing pointwise uncertainty regions for a scalar β with ignorance region [βl, βu]. Let γl, γu ∈ Γ be the values of the sensitivity parameter such that βl = β(γl) and βu = β(γu). Assume
| (38) |
| (39) |
Under assumptions (38) and (39), an asymptotic (1 − α) pointwise uncertainty interval for β0 is
| (40) |
where cα satisfies
| (41) |
Φ(·) denotes the cumulative distribution function of a standard normal variate, and σ̂l and σ̂u are consistent estimators of σl and σu, respectively (Imbens and Manski, 2004; Vansteelandt et al., 2006). Note if β̂u − β̂l > 0 and n is large such that the left-hand side of (41) is approximately equal to 1 − Φ(−cα), then cα ≈ z1 − α, the (1 − α) quantile of a standard normal distribution. In contrast, if β̂u = β̂l, then cα = z1 − α/2.
In addition to the pointwise uncertainty region, Horowitz and Manski (2000) and Vansteelandt et al. (2006) define a (1 − α) strong uncertainty region for β0 to be a region URs(β, Γ) such that
that is, URs(β, Γ) contains the entire ignorance region with probability at least 1 − α. Whereas the pointwise uncertainty region can be viewed as a confidence region for the partially identifiable target parameter β0, the strong uncertainty region is a confidence region for the ignorance region irf0(β, Γ). Clearly, any strong uncertainty region will also be a (conservative) pointwise uncertainty region as β0 ∈ irf0(β, Γ). Under assumptions (38) and (39), an asymptotic (1 − α) strong uncertainty interval for scalar β0 is simply
| (42) |
Note that (42) is equivalent to the union of all pointwise (1 − α) confidence intervals for β(γ) under
 (γ) over all γ ∈ Γ, which is a simple approach often employed when reporting sensitivity analysis. Because strong uncertainty intervals are necessarily pointwise intervals, this simple approach is also a valid method for computing pointwise intervals, although intervals based on (40) will always be as or more narrow.
(γ) over all γ ∈ Γ, which is a simple approach often employed when reporting sensitivity analysis. Because strong uncertainty intervals are necessarily pointwise intervals, this simple approach is also a valid method for computing pointwise intervals, although intervals based on (40) will always be as or more narrow.
The two key assumptions (38) and (39) may not hold in general. For example, (38) may not hold for all possible observed data distributions, particularly for extreme values of γl or γu. Assumption (39) may not hold if different observed data distributions place different constraints on the possible range of γ or if Γ is chosen by the data analyst on the basis of the observed data. If (38) or (39) does not hold, alternative inferential methods are needed (e.g., see Vansteelandt and Goetghebeur, 2001; Horowitz and Manski, 2006; Chernozhukov, Hong and Tamer, 2007; Romano and Shaikh, 2008; Stoye, 2009; Todem, Fine and Peng, 2010; Bugni, 2010).
A third approach to quantifying uncertainty due to sampling variability is to consider β(·) as function of γ and construct a (1 − α) simultaneous confidence band for the function β(·). That is, a random function CB(·) is found such that
It follows immediately that ⋃γ ∈ Γ CB(γ) is a strong uncertainty region (and thus a pointwise uncertainty region as well). Todem, Fine and Peng (2010) suggest a bootstrap approach to constructing confidence bands.
Whether pointwise uncertainty regions, strong uncertainty regions, or confidence bands are preferred will be context specific. Typically, it is of interest to draw inference about a single target parameter and not the entire ignorance region. Thus, in general pointwise uncertainty regions may have greater utility than strong uncertainty regions. Because strong uncertainty regions are necessarily conservative pointwise uncertainty regions, the strong regions can be useful in settings where determining a pointwise region is more difficult. Additionally, in some settings it may be of interest to assess whether β is nonzero, for example, if β denotes the effect of treatment. In these settings, computing a confidence band CB(·) has the advantage of providing the subset of Γ where the null hypothesis β(γ) = 0 can be rejected. This is especially appealing if γ is scalar, in which case a confidence band (as in Figure 3 of Todem, Fine and Peng, 2010) provides a simple approach to reporting sensitivity analysis results. On the other hand, if γ is multidimensional, visualizing confidence bands can be difficult and instead reporting the (pointwise or strong) uncertainty region may be more practical.
7.3 Data Example
Returning to the pertussis vaccine study described in Section 3, an analysis that ignores the potential for selection bias might entail computing a naive estimator (the difference in empirical means of Y between the vaccinated and unvaccinated amongst those infected) along with a 95% Wald confidence interval, which would be −0.31 (95% CI −0.38, −0.23). If the sensitivity analysis approach in Section 3.4 is applied, the parameter of interest β(γ) = E[Y(1) − Y(0)|SP0 = (1, 1)] is identified for fixed values of the sensitivity analysis parameter γ given in (19). For fixed γ, E[Y(0)|SP0 = (1, 1)] is determined by the intersection of the negative sloped line (14) and the curve (19), which is illustrated in Figure 1 for the pertussis data. Because E[Y(0)|SP0 = (1, 1)] increases with γ, β(γ) is a monotonically decreasing function of γ. Therefore γl and γu equal the maximum and minimum values of Γ regardless of the observed data law, indicating (39) holds provided that Γ is chosen by the analyst independent of the observed data. For γ fixed and finite, β(γ) can be estimated via nonparametric maximum likelihood (i.e., without any additional assumptions). This estimator will be consistent and asymptotically normal under standard regularity conditions if Pr[S(0) > S(1)] > 0 (i.e., the vaccine has a protective effect against infection). For γ = ±∞ and Pr[S(0) > S(1)] > 0, Lee (2009) proved that the estimators of the bounds similar to those given in Section 3.3 are consistent and asymptotically normal for a continuous outcome Y. The limiting distribution of the estimator of the upper bound (γ = −∞) for a binary outcome will be normal if in addition
| (43) |
and similarly the estimator of the lower bound (γ = ∞) will be asymptotically normal if in addition
| (44) |
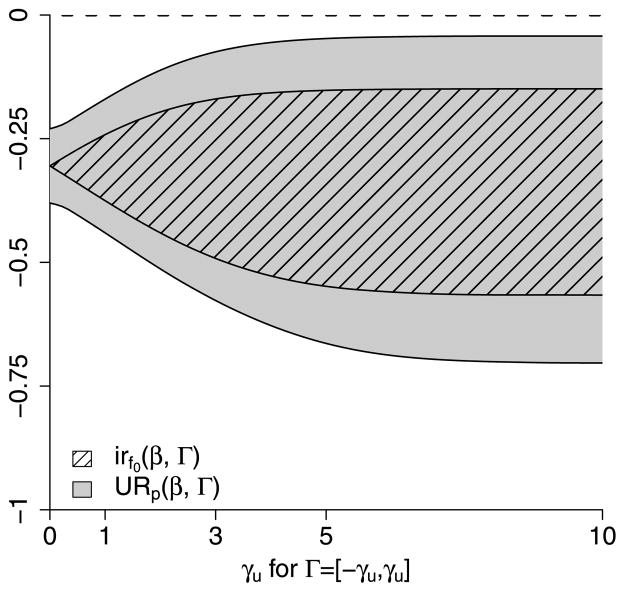
Likelihood ratio tests for the null hypotheses that (43) and (44) do not hold yield p-values p < 10−4 and p = 0.18, respectively, indicating strong evidence that (43) holds and equivocal evidence regarding (44). Assuming (43) and (44) both hold implies (38), such that (40) and (42) can be used to construct (1 − α) pointwise and strong uncertainty intervals for β0. Estimated ignorance and uncertainty intervals of β0 for different choices of Γ are given in Table 1 and Figure 2, with standard error estimates obtained using the observed information. Even for Γ = (−∞, ∞) both the pointwise and strong uncertainty intervals exclude zero, indicating a significant effect of vaccination. In particular, with 95% confidence we can conclude the vaccine decreased the risk of severe disease among individuals who would have become infected regardless of vaccination.
Table 1.
Pertussis vaccine study data: Estimated ignorance regions and 95% pointwise and strong uncertainty regions of β = E[Y(1) − Y(0)|SP0 = (1, 1)] for different Γ
| Γ | irf0(β, Γ) | URp(β, Γ) | URs(β, Γ) |
|---|---|---|---|
| [−3, 3] | [−0.49, −0.17] | [−0.58, −0.07] | [−0.59, −0.06] |
| [−5, 5] | [−0.55, −0.15] | [−0.66, −0.05] | [−0.69, −0.03] |
| [−10, 10] | [−0.57, −0.15] | [−0.70, −0.04] | [−0.73, −0.02] |
| (−∞, ∞) | [−0.57, −0.15] | [−0.70, −0.04] | [−0.73, −0.02] |
Fig. 2.
Estimated ignorance regions irf0(β, Γ) and 95% pointwise uncertainty regions URp(β, Γ) for the pertussis vaccine example in Section 7.3. The principal effect (10) is denoted β and Γ = [−γu, γu] for γu along the horizontal axis. The curve given by the lower boundary of the area with black slanted lines corresponds to β̂l, the minimum of the estimated ignorance regions, and the upper bound of the area with black slanted lines corresponds to β̂u, the maximum of the estimated ignorance region. The curve given by the lower (upper) boundary of the gray shaded area corresponds to the minimum (maximum) of the 95% pointwise uncertainty region.
8. DISCUSSION
This paper considers conducting inference about the effect of a treatment (or exposure) on an outcome of interest. Unless treatment is randomly assigned and there is perfect compliance, the effect of treatment may be only partially identifiable from the observable data. Through the five settings in Sections 2–6, we discussed two approaches often employed to address partial identifiability: (i) bounding the treatment effect under minimal assumptions, or (ii) invoking additional untestable assumptions that render the treatment effect identifiable and then conducting sensitivity analysis to assess how inference about the treatment effect changes as the untestable assumptions are varied. Incorporating uncertainty due to sampling variability was discussed in Section 7, and throughout large-sample frequentist methods were considered. Analogous Bayesian approaches to partial identification (Gustafson, 2010; Moon and Schorfheide, 2012; Richardson, Evans and Robins, 2011) and sensitivity analysis (McCandless, Gustafson and Levy, 2007; Gustafson et al., 2010) have also been developed.
Determining treatment effect bounds is essentially a constrained optimization problem, where the constraints are determined by the relationship between the distributions of the observable random variables and of the potential outcomes under whichever assumptions are being made. In simple cases, such as in Section 2.1, bounds can easily be derived from first principles and may have simple closed forms; in more complicated settings, such as in Section 4, bounds may be determined using linear programming or other optimization methods. In many cases, calculating bounds under minimal assumptions may seem to be a meaningless exercise because the bounds are often quite wide and may not exclude the null of no treatment effect as seen with the “no assumptions” bounds in Section 2. On the contrary, in settings like this Robins and Greenland (1996) write: “Some argue against reporting bounds for non-identifiable parameters, because bounds are often so wide as to be useless for making public health decisions. But we view the latter problem as a reason for reporting bounds in conjunction with other analyses: Wide bounds make clear that the degree to which public health decisions are dependent on merging the data with strong prior beliefs.”
Bounds may be narrowed by reducing the feasible region of the optimization problem. This may be accomplished by considering further assumptions that place restrictions on either the distributions of the potential outcomes, the distributions of the observable random variables, or both. Assumptions that place restrictions on the observable random variables may have implications which are testable. If the observed data provide evidence against any assumptions being considered, bounds should be computed without making these assumptions. Those assumptions without testable implications can only be determined to be plausible or not by subject matter experts.
A potentially less conservative approach to computing bounds is to make untestable assumptions which identify the causal estimand and then assess the robustness of inference drawn to departures from these assumptions in a sensitivity analysis. A general guideline for specifying the sensitivity analysis parameters representing these departures is to choose parameters that are easily interpretable to subject matter experts. Parameter specification will depend on whether or not sensitivity analysis is conducted by directly modeling the association of an unmeasured confounder U with treatment selection and the potential outcomes. Sensitivity analyses based on this approach are applicable when the existence of U is known and there is some historical knowledge of the magnitude association of U with Z and the potential outcomes (Robins, 1999; Brumback et al., 2004). Otherwise, alternative approaches based on directly modeling the unobserved potential outcome distributions may be preferred. A second guiding principle should be to avoid specifications of sensitivity parameters that place restrictions on the distributions of observable random variables that are not empirically supported. A third consideration when conducting sensitivity analysis concerns determining a plausible region of the sensitivity parameters. That the region be chosen prior to data analysis is in general necessary for inference, such as described in Section 7, to be valid. Choice of the region of the sensitivity parameters may be dictated by whether one wants to consider only mild or also severe departures from the identifying assumptions. If the identifying assumption in question is considered plausible, then it may be that only mild departures from the assumption are deemed necessary for the sensitivity analysis. In this case, subject matter experts can be consulted to determine, prior to data analysis, a plausible region for the sensitivity parameters. If, on the other hand, severe departures from untestable identifying assumptions are to be entertained, sensitivity analyses should be conducted over all possible values of the sensitivity parameters. Sensitivity analyses which consider all possible full data distributions that marginalize to the observed data distribution will yield ignorance regions containing the bounds.
Though the examples presented here demonstrate the broad scope of scenarios where bounds and sensitivity analysis methods have been derived and employed to draw inference about treatment effects, they certainly are not exhaustive of all settings where these methods have been developed. For instance, VanderWeele, Mukherjee and Chen (2012) consider sensitivity analysis to unmeasured confounding for causal interaction effects. Bounds and sensitivity analysis methods have also recently been considered in the presence of interference, that is, in settings where treatment of one individual may affect the outcome of another individual, such as in social networks (Ver Steeg and Galstyan, 2010; VanderWeele, 2011b; Manski, 2013). For studies where sensitivity analyses are planned or anticipated, Rosenbaum and colleagues have examined how aspects of study design and the choice of statistical tests or estimators may affect the power or precision of the sensitivity analyses to be conducted (Heller, Rosenbaum and Small, 2009; Rosenbaum, 2010a; 2010b; 2011).
Bounds and sensitivity analyses of treatment effects have been utilized in various substantive settings, such as biomedical research (e.g., Cole et al., 2005; Rerks-Ngarm et al., 2009; VanderWeele and Hernández-Diaz, 2011; Hu et al., 2012) and economics (e.g., Heckman, 2001; Sianesi, 2004; Armstrong, Guay and Weber, 2010). Nonetheless, despite the wide range of settings in which these methods are applicable, their use in substantive settings remains somewhat limited in frequency. Given the large amount of literature detailing their broad scope of applicability and that formal inferential methods for partially identifiable parameters are now available, hopefully these approaches will be employed with greater frequency in substantive settings in the future.
The sensitivity analyses described throughout this paper focus on departures from untestable assumptions which identify treatment effects. Other types of sensitivity analyses might be considered as well, for example, to assess how robust inferences are to various analytical decisions that are invariably made in data analysis. Rosenbaum (2002, Section 11.9) refers to such assessment as “stability analysis,” in contrast to the types of sensitivity analyses discussed above. See Rosenbaum (1999, 2002) and Morgan and Winship (2007, Section 6.2) for further discussion regarding various types of sensitivity analyses beyond the type considered here.
Acknowledgments
The authors were partially supported by NIH NIAID grants R01 AI085073 and R37 AI054165. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute of Allergy and Infectious Diseases or the National Institutes of Health. The authors thank Guest Editors Andrea Rotnitzky and Thomas Richardson for the invitation to contribute to this special issue of Statistical Science; and the Associate Editor and reviewers for their helpful comments. This paper was written while the first author was a Ph.D. student in the Department of Biostatistics at the University of North Carolina.
Contributor Information
Amy Richardson, Email: amyrichardson@google.com, Quantitative Analyst, Google Inc., Mountain View, California 94043, USA.
Michael G. Hudgens, Email: mhudgens@bios.unc.edu, Associate Professor, Department of Biostatistics, University of North Carolina at Chapel Hill, Chapel Hill, North Carolina 27599, USA
Peter B. Gilbert, Email: pgilbert@scharp.org, Member, Statistical Center for HIV/AIDS Research and Prevention (SCHARP), Fred Hutchinson Cancer Research Center, Seattle, Washington 98109-1024, USA
Jason P. Fine, Email: jfine@bios.unc.edu, Professor, Department of Biostatistics, University of North Carolina at Chapel Hill, Chapel Hill, North Carolina 27599, USA
References
- Angrist JD, Imbens GW, Rubin DB. Identification of causal effects using instrumental variables. J Amer Statist Assoc. 1996;91:444–455. [Google Scholar]
- Armstrong CS, Guay WR, Weber JP. The role of information and financial reporting in corporate governance and debt contracting. J Accounting and Economics. 2010;50:179–234. [Google Scholar]
- Balke A, Pearl J. Technical report. Univ. California; Los Angeles: 1993. Nonparametric bounds on causal effects from partial compliance data. [Google Scholar]
- Balke A, Pearl J. Bounds on treatment effects from studies with imperfect compliance. J Amer Statist Assoc. 1997;92:1171–1177. [Google Scholar]
- Brumback BA, Hernán MA, Haneuse SJPA, Robins JM. Sensitivity analyses for unmeasured confounding assuming a marginal structural model for repeated measures. Stat Med. 2004;23:749–767. doi: 10.1002/sim.1657. [DOI] [PubMed] [Google Scholar]
- Bugni FA. Bootstrap inference in partially identified models defined by moment inequalities: Coverage of the identified set. Econometrica. 2010;78:735–753. MR2656646. [Google Scholar]
- Cai Z, Kuroki M, Pearl J, Tian J. Bounds on direct effects in the presence of confounded intermediate variables. Biometrics. 2008;64:695–701. doi: 10.1111/j.1541-0420.2007.00949.x. MR2526618. [DOI] [PubMed] [Google Scholar]
- Chernozhukov V, Hong H, Tamer E. Estimation and confidence regions for parameter sets in econometric models. Econometrica. 2007;75:1243–1284. MR2347346. [Google Scholar]
- Chiburis RC. Semiparametric bounds on treatment effects. J Econometrics. 2010;159:267–275. MR2733120. [Google Scholar]
- Chickering DM, Pearl J. AAAI-96 Proceedings. AAAI Press; Menlo Park, CA: 1996. A clinician’s tool for analyzing non-compliance; pp. 1269–1276. [Google Scholar]
- Cole SR, Hernán MA, Margolick JB, Cohen MH, Robins JM. Marginal structural models for estimating the effect of highly active antiretroviral therapy initiation on CD4 cell count. Amer J Epidemiol. 2005;162:471–478. doi: 10.1093/aje/kwi216. [DOI] [PubMed] [Google Scholar]
- Cornfield J, Haenszel W, Hammond EC, Lilienfeld AM, Shimkin MB, Wynder EL. Smoking and lung cancer: Recent evidence and a discussion of some questions. J Natl Cancer Inst. 1959;22:173–203. [PubMed] [Google Scholar]
- Dawid AP. Causal inference using influence diagrams: The problem of partial compliance. In: Green PJ, Hjort NL, Richardson S, editors. Highly Structured Stochastic Systems. Oxford Univ. Press; Oxford: 2003. pp. 45–81. MR2082406. [Google Scholar]
- Frangakis CE, Rubin DB. Principal stratification in causal inference. Biometrics. 2002;58:21–29. doi: 10.1111/j.0006-341x.2002.00021.x. MR1891039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert PB, Bosch RJ, Hudgens MG. Sensitivity analysis for the assessment of causal vaccine effects on viral load in HIV vaccine trials. Biometrics. 2003;59:531–541. doi: 10.1111/1541-0420.00063. MR2004258. [DOI] [PubMed] [Google Scholar]
- Grilli L, Mealli F. Nonparametric bounds on the causal effect of university studies on job opportunities using principal stratification. J Educ Behav Stat. 2008;33:111–130. [Google Scholar]
- Gustafson P. Bayesian inference for partially identified models. Int J Biostat. 2010;6:1–18. doi: 10.2202/1557-4679.1206. MR2602560. [DOI] [PubMed] [Google Scholar]
- Gustafson P, McCandless LC, Levy AR, Richardson S. Simplified Bayesian sensitivity analysis for mismeasured and unobserved confounders. Biometrics. 2010;66:1129–1137. doi: 10.1111/j.1541-0420.2009.01377.x. MR2758500. [DOI] [PubMed] [Google Scholar]
- Hafeman DM. Confounding of indirect effects: A sensitivity analysis exploring the range of bias due to a cause common to both the mediator and the outcome. Amer J Epidemiol. 2011;174:710–717. doi: 10.1093/aje/kwr173. [DOI] [PubMed] [Google Scholar]
- Heckman JJ. Micro data, heterogeneity, and the evaluation of public policy: Nobel lecture. J Political Economy. 2001;109:673–748. [Google Scholar]
- Heller R, Rosenbaum PR, Small DS. Split samples and design sensitivity in observational studies. J Amer Statist Assoc. 2009;104:1090–1101. MR2750238. [Google Scholar]
- Hernán MA, Robins JM. Assessing the sensitivity of regression results to unmeasured confounders in observational studies [letter] Biometrics. 1999;55:1316–1317. [PubMed] [Google Scholar]
- Hernán MA, Robins JM. Instruments for causal inference: An epidemiologist’s dream? Epidemiology. 2006;17:360– 372. doi: 10.1097/01.ede.0000222409.00878.37. [DOI] [PubMed] [Google Scholar]
- Horowitz JL, Manski CF. Nonparametric analysis of randomized experiments with missing covariate and outcome data. J Amer Statist Assoc. 2000;95:77–84. MR1803142. [Google Scholar]
- Horowitz JL, Manski CF. Identification and estimation of statistical functionals using incomplete data. J Econometrics. 2006;132:445–459. MR2323988. [Google Scholar]
- Hu JC, Williams SB, O’Malley AJ, Smith MR, Nguyen PL, Keating NL. Androgen-deprivation therapy for nonmetastatic prostate cancer is associated with an increased risk of peripheral arterial disease and venous thromboembolism. Eur Urol. 2012;61:1119–1128. doi: 10.1016/j.eururo.2012.01.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudgens MG, Halloran ME. Causal vaccine effects on binary postinfection outcomes. J Amer Statist Assoc. 2006;101:51–64. doi: 10.1198/016214505000000970. MR2252433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudgens MG, Hoering A, Self SG. On the analysis of viral load endpoints in HIV vaccine trials. Stat Med. 2003;22:2281–2298. doi: 10.1002/sim.1394. [DOI] [PubMed] [Google Scholar]
- Imai K, Keele L, Yamamoto T. Identification, inference and sensitivity analysis for causal mediation effects. Statist Sci. 2010;25:51–71. MR2741814. [Google Scholar]
- Imbens GW, Angrist JD. Identification and estimation of local average treatment effects. Econometrica. 1994;62:467–475. [Google Scholar]
- Imbens GW, Manski CF. Confidence intervals for partially identified parameters. Econometrica. 2004;72:1845–1857. MR2095534. [Google Scholar]
- Joffe M. Principal stratification and attribution prohibition: Good ideas taken too far. Int J Biostat. 2011;7:1–22. doi: 10.2202/1557-4679.1367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufman S, Kaufman JS, MacLehose RF. Analytic bounds on causal risk differences in directed acyclic graphs involving three observed binary variables. J Statist Plann Inference. 2009;139:3473–3487. doi: 10.1016/j.jspi.2009.03.024. MR2549096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee M-j. Micro-econometrics for Policy, Program, and Treatment Effects. Oxford Univ. Press; Oxford: 2005. MR2261528. [Google Scholar]
- Lee DS. Training, wages, and sample selection: Estimating sharp bounds on treatment effects. Rev Econom Stud. 2009;76:1071–1102. [Google Scholar]
- Lin DY, Psaty BM, Kronmal RA. Assessing the sensitivity of regression results to unmeasured confounders in observational studies. Biometrics. 1998;54:948–963. [PubMed] [Google Scholar]
- Long DM, Hudgens MG. Sharpening bounds on principal effects with covariates. Biometrics. 2013;69:812–819. doi: 10.1111/biom.12103. MR3146777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manski CF. Nonparametric bounds on treatment effects. Am Econ Rev. 1990;80:319–323. [Google Scholar]
- Manski CF. Monotone treatment response. Econometrica. 1997;65:1311–1334. MR1604297. [Google Scholar]
- Manski CF. Identification of treatment response with social interactions. Econom J. 2013;16:S1–S23. MR3030060. [Google Scholar]
- Manski CF, Pepper JV. Monotone instrumental variables: With an application to the returns to schooling. Econometrica. 2000;68:997–1010. MR1771587. [Google Scholar]
- McCandless LC, Gustafson P, Levy A. Bayesian sensitivity analysis for unmeasured confounding in observational studies. Stat Med. 2007;26:2331–2347. doi: 10.1002/sim.2711. MR2368419. [DOI] [PubMed] [Google Scholar]
- Moon HR, Schorfheide F. Bayesian and frequentist inference in partially identified models. Econometrica. 2012;80:755–782. MR2951948. [Google Scholar]
- Morgan SL, Winship C. Counterfactuals and Causal Inference. Cambridge Univ. Press; New York: 2007. [Google Scholar]
- Pearl J. Direct and indirect effects. Proceedings of the 17th Conference in Uncertainty in Artificial Intelligence. UAI’01; San Francisco, CA: Morgan Kaufmann; 2001. pp. 411–420. [Google Scholar]
- Pearl J. Causality: Models, Reasoning, and Inference. 2. Cambridge Univ. Press; Cambridge: 2009. MR2548166. [Google Scholar]
- Pearl J. On the consistency rule in causal inference: Axiom, definition, assumption, or theorem? Epidemiology. 2010;21:872–875. doi: 10.1097/EDE.0b013e3181f5d3fd. [DOI] [PubMed] [Google Scholar]
- Pearl J. Principal stratification: A goal or a tool? Int J Biostat. 2011;7:1–14. doi: 10.2202/1557-4679.1322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Préziosi MP, Halloran ME. Effects of pertussis vaccination on disease: Vaccine efficacy in reducing clinical severity. Clin Infect Dis. 2003;37:772–779. doi: 10.1086/377270. [DOI] [PubMed] [Google Scholar]
- Rerks-Ngarm S, Pitisuttithum P, Nitayaphan S, Kaewkungwal J, Chiu J, Paris R, Premsri N, Namwat C, de Souza M, Adams E, Benenson M, Gurunathan S, Tartaglia J, McNeil JG, Francis DP, Stablein D, Birx DL, Chunsuttiwat S, Khamboonruang C, Thongcharoen P, Robb ML, Michael NL, Kunasol P, Kim JH. Vaccination with ALVAC and AIDSVAX to prevent HIV-1 infection in Thailand. N Engl J Med. 2009;361:2209–2220. doi: 10.1056/NEJMoa0908492. [DOI] [PubMed] [Google Scholar]
- Richardson TS, Evans RJ, Robins JM. Transparent parametrizations of models for potential outcomes. In: Bernardo JM, Bayarri MJ, Berger JO, Dawid AP, Heckerman D, Smith AFM, West M, editors. Bayesian Statistics. Vol. 9. Oxford Univ. Press; Oxford: 2011. pp. 569–610. MR3204019. [Google Scholar]
- Robins JM. The analysis of randomized and non-randomized AIDS treatment trials using a new approach to causal inference in longitudinal studies. Health Service Research Methodology: A Focus on AIDS. 1989:113–159. [Google Scholar]
- Robins JM. Correcting for non-compliance in randomized trials using structural nested mean models. Comm Statist Theory Methods. 1994;23:2379–2412. MR1293185. [Google Scholar]
- Robins JM. Non-response models for the analysis of non-monotone non-ignorable missing data. Stat Med. 1997;16:21–37. doi: 10.1002/(sici)1097-0258(19970115)16:1<21::aid-sim470>3.0.co;2-f. [DOI] [PubMed] [Google Scholar]
- Robins JM. Association, causation, and marginal structural models. Statistics and causation. Synthese. 1999;121:151–179. MR1766776. [Google Scholar]
- Robins JM. Comment on “Covariance adjustment in randomized experiments and observational studies”. Statist Sci. 2002;17:309–321. [Google Scholar]
- Robins JM. Semantics of causal DAG models and the identification of direct and indirect effects. Oxford Statist Sci Ser. 2003:70–82. [Google Scholar]
- Robins JM, Greenland S. Identifiability and exchangeability for direct and indirect effects. Epidemiology. 1992;3:143–155. doi: 10.1097/00001648-199203000-00013. [DOI] [PubMed] [Google Scholar]
- Robins JM, Greenland S. Comment on “Identification of causal effects using instrumental variables” by Angrist, Imbens and Rubin. J Amer Statist Assoc. 1996;91:456–458. [Google Scholar]
- Robins JM, Richardson TS. Alternative graphical causal models and the identification of direct effects. In: Shrout P, editor. Causality and Psychopathology: Finding the Determinants of Disorders and Their Cures. Oxford Univ. Press; Oxford: 2010. [Google Scholar]
- Robins JM, Rotnitzky A, Scharfstein DO. Statistical Models in Epidemiology, the Environment, and Clinical Trials (Minneapolis, MN, 1997) IMA Vol Math Appl. Vol. 116. Springer; New York: 2000. Sensitivity analysis for selection bias and unmeasured confounding in missing data and causal inference models; pp. 1–94. MR1731681. [Google Scholar]
- Romano JP, Shaikh AM. Inference for identifiable parameters in partially identified econometric models. J Statist Plann Inference. 2008;138:2786–2807. MR2422399. [Google Scholar]
- Rosenbaum PR. Choice as an alternative to control in observational studies. Statist Sci. 1999;14:259–278. [Google Scholar]
- Rosenbaum PR. Observational Studies. 2. Springer; New York: 2002. MR1899138. [Google Scholar]
- Rosenbaum PR. Design sensitivity and efficiency in observational studies. J Amer Statist Assoc. 2010a;105:692–702. MR2724853. [Google Scholar]
- Rosenbaum PR. Evidence factors in observational studies. Biometrika. 2010b;97:333–345. MR2650742. [Google Scholar]
- Rosenbaum PR. Some approximate evidence factors in observational studies. J Amer Statist Assoc. 2011;106:285–295. MR2816721. [Google Scholar]
- Rosenbaum PR, Rubin DB. Assessing sensitivity to an unobserved binary covariate in an observational study with binary outcome. J R Stat Soc Ser B Stat Methodol. 1983;45:212–218. [Google Scholar]
- Rotnitzky A, Jemiai Y. Sharp bounds and sensitivity analysis for treatment effects in the presence of censoring by death. Harvard Schering-Plough Workshop on Development and Approval of Oncology Drug Products: Impact of Statistics.2003. [Google Scholar]
- Rubin DB. Discussion of “Randomization analysis of experimental data in the Fisher randomization test,” by D. Basu. J Amer Statist Assoc. 1980;75:591–593. [Google Scholar]
- Rubin DB. Comment on “Causal inference without counterfactuals”. J Amer Statist Assoc. 2000;95:435–437. [Google Scholar]
- Scharfstein DO, Rotnitzky A, Robins JM. Adjusting for nonignorable drop-out using semiparametric nonresponse models. J Amer Statist Assoc. 1999;94:1096–1146. MR1731478. [Google Scholar]
- Schlesselman JJ. Assessing effects of confounding variables. Amer J Epidemiol. 1978;108:3–8. [PubMed] [Google Scholar]
- Shepherd BE, Gilbert PB, Mehrotra DV. Eliciting a counterfactual sensitivity parameter. Amer Statist. 2007;61:56–63. MR2339148. [Google Scholar]
- Sianesi B. An evaluation of the Swedish system of active labor market programs in the 1990s. The Review of Economics and Statistics. 2004;86:133–155. [Google Scholar]
- Sjölander A. Bounds on natural direct effects in the presence of confounded intermediate variables. Stat Med. 2009;28:558–571. doi: 10.1002/sim.3493. MR2655730. [DOI] [PubMed] [Google Scholar]
- Stoye J. More on confidence intervals for partially identified parameters. Econometrica. 2009;77:1299–1315. MR2547075. [Google Scholar]
- Tchetgen Tchetgen EJ, Glymour MM, Weuve J, Robins J. Technical Report 140, Harvard Univ. Biostatistics Working Paper Series. 2012a. A cautionary note on specification of the correlation structure in inverse-probability-weighted estimation for repeated measures. [Google Scholar]
- Tchetgen Tchetgen EJT, Glymour MM, Weuve J, Robins J. Specifying the correlation structure in inverse-probability-weighting estimation for repeated measures. Epidemiology. 2012b;23:644–646. doi: 10.1097/EDE.0b013e31825727b5. [DOI] [PubMed] [Google Scholar]
- Todem D, Fine J, Peng L. A global sensitivity test for evaluating statistical hypotheses with nonidentifiable models. Biometrics. 2010;66:558–566. doi: 10.1111/j.1541-0420.2009.01290.x. MR2758836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele TJ. Sensitivity analysis: Distributional assumptions and confounding assumptions. Biometrics. 2008;64:645–649. doi: 10.1111/j.1541-0420.2008.01024.x. MR2432439. [DOI] [PubMed] [Google Scholar]
- VanderWeele TJ. Bias formulas for sensitivity analysis for direct and indirect effects. Epidemiology. 2010;21:540–551. doi: 10.1097/EDE.0b013e3181df191c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele TJ. Controlled direct and mediated effects: Definition, identification and bounds. Scand J Stat. 2011a;38:551–563. doi: 10.1111/j.1467-9469.2010.00722.x. MR2833846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele TJ. Sensitivity analysis for contagion effects in social networks. Sociol Methods Res. 2011b;40:240–255. doi: 10.1177/0049124111404821. MR2767834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele TJ, Arah OA. Bias formulas for sensitivity analysis of unmeasured confounding for general outcomes, treatments, and confounders. Epidemiology. 2011;22:42–52. doi: 10.1097/EDE.0b013e3181f74493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele TJ, Hernández-Diaz S. Is there a direct effect of pre-eclampsia on cerebral palsy not through preterm birth? Paediatric and Perinatal Epidemiology. 2011;25:111–115. doi: 10.1111/j.1365-3016.2010.01175.x. [DOI] [PubMed] [Google Scholar]
- VanderWeele TJ, Mukherjee B, Chen J. Sensitivity analysis for interactions under unmeasured confounding. Stat Med. 2012;31:2552–2564. doi: 10.1002/sim.4354. MR2972267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vansteelandt S, Goetghebeur E. Analyzing the sensitivity of generalized linear models to incomplete outcomes via the IDE algorithm. J Comput Graph Statist. 2001;10:656–672. MR1938973. [Google Scholar]
- Vansteelandt S, Goetghebeur E, Kenward MG, Molenberghs G. Ignorance and uncertainty regions as inferential tools in a sensitivity analysis. Statist Sinica. 2006;16:953–979. MR2281311. [Google Scholar]
- van der Laan MJ, Robins JM. Unified Methods for Censored Longitudinal Data and Causality. Springer; New York: 2003. MR1958123. [Google Scholar]
- Ver Steeg G, Galstyan A. Ruling out latent homophily in social networks. NIPS Workshop on Social Computing.2010. [Google Scholar]
- Zhang JL, Rubin DB. Estimation of causal effects via principal stratification when some outcomes are truncated by “death. J Educational and Behavioral Statistics. 2003;28:353–368. [Google Scholar]