Imaging Dirac-mass disorder from magnetic dopant atoms in the ferromagnetic topological insulator Cr_x(Bi_0.1Sb_0.9)_2-xTe₃

Significance

Surface states of topological insulators (TIs) should exhibit extraordinary electronic phenomena when a ‘Dirac-mass gap’ is opened in their spectrum, typically by creating a ferromagnetic state. However, our direct visualization of the Dirac-mass gap $\Delta \left(r\right)$ in a ferromagnetic TI reveals its intense disorder at the nanoscale. This is correlated with the density of magnetic dopant atoms $n\left(r\right)$, such that $\mathrm{\Delta }\left(r\right)\propto n\left(r\right)$ as anticipated for surface-state–mediated ferromagnetism. Consequent new perspectives on ferromagnetic TI physics include that the quantum anomalous Hall effect occurs in this environment of extreme Dirac-mass disorder and that paths of associated chiral edge states must be tortuous. To achieve all the exotic physics expected of ferromagnetic TIs, greatly improved control of dopant-induced Dirac-mass gap disorder is therefore required.

Abstract

To achieve and use the most exotic electronic phenomena predicted for the surface states of 3D topological insulators (TIs), it is necessary to open a “Dirac-mass gap” in their spectrum by breaking time-reversal symmetry. Use of magnetic dopant atoms to generate a ferromagnetic state is the most widely applied approach. However, it is unknown how the spatial arrangements of the magnetic dopant atoms influence the Dirac-mass gap at the atomic scale or, conversely, whether the ferromagnetic interactions between dopant atoms are influenced by the topological surface states. Here we image the locations of the magnetic (Cr) dopant atoms in the ferromagnetic TI Cr_0.08(Bi_0.1Sb_0.9)_1.92Te₃. Simultaneous visualization of the Dirac-mass gap Δ(r) reveals its intense disorder, which we demonstrate is directly related to fluctuations in n(r), the Cr atom areal density in the termination layer. We find the relationship of surface-state Fermi wavevectors to the anisotropic structure of Δ(r) not inconsistent with predictions for surface ferromagnetism mediated by those states. Moreover, despite the intense Dirac-mass disorder, the anticipated relationship $\mathrm{\Delta }\left(\mathit{r}\right)\propto \mathit{n}\left(\mathit{r}\right)$ is confirmed throughout and exhibits an electron–dopant interaction energy J* = 145 meV·nm². These observations reveal how magnetic dopant atoms actually generate the TI mass gap locally and that, to achieve the novel physics expected of time-reversal symmetry breaking TI materials, control of the resulting Dirac-mass gap disorder will be essential.

That the surface states of 3D topological insulators (TIs) exhibit a “massless” Dirac spectrum $E\left(\mathit{k}\right)=\hslash v\mathit{k}\mathrm{\cdot }\mathit{\sigma }$ with spin-momentum locking and protected by time-reversal symmetry is now firmly established. Opening a gap in this spectrum is key to the realization of several extraordinary new types of electronic phenomena. The prevalent approach to opening this “Dirac-mass gap” is to dope the materials with magnetic atoms (1–6). A plethora of new physics is then predicted, including ${\sigma }_{xy}=\pm e^2/h$ quantum anomalous Hall effects (QAHE) (7, 8), topological surface-state magneto-electric effects (9–12), related magneto-optical Kerr and Faraday rotations (10, 13, 14), axionic-like electrodynamics (15, 16), and even E-field induced magnetic monopoles (17, 18). As yet, none of these phenomena except the QAHE (19–22) have been detected, and the QAHE itself is poorly understood because ${\sigma }_{xy}=\pm e^2/h$ is observed only at temperatures far below 1 K.

Interactions between the TI surface electrons and the magnetic dopant atoms at random surface locations ${\mathit{r}}_i$ can be represented theoretically by a Hamiltonian of the type $H_{DA}=-J^{\ast }{{\displaystyle \sum }}^{}{\mathit{S}}_i·\mathit{s}\delta \left(\mathit{r}-{\mathit{r}}_i\right)$. Here ${\mathit{S}}_i$ (s) is the spin of each dopant (surface-state carrier) measured in units of $\hslash$, and $J^{\ast }$ is their exchange-interaction energy scale. In the simple case of a homogenous ferromagnetic state with magnetization parallel to the surface normal $\widehat{z}$, the Hamiltonian becomes $H=-J^{\ast }{n}_0{S}_z{\sigma }_3/2$, where $n_0$ is the average 2D dopant-atom density and S_z the magnitude of the z component of the dopant spin. Such interactions should open a Zeeman-like energy gap of magnitude $\Delta =J^{\ast }{M}_z/2{\mu }_B\left(\equiv m{v}^2\right)$, where $M_z=n_0{S}_z{\mu }_B$ is the homogeneous $\widehat{z}$-aligned magnetization, m is the Dirac mass, and v is the Fermi velocity. The resulting surface-state dispersion is given by $E_{\pm }\left(k\right)=E_D\pm \sqrt{{\left(\hslash v\right)}^2{k}^2+{\Delta }^2}$, where E_D is the Dirac point of the ungapped bands measured relative to the surface-state Fermi energy $E_F$, and Δ is the Dirac-mass gap. Angle-resolved photoemission studies provide good evidence that high densities of magnetic dopant atoms generate a ferromagnetic state and open such energy gaps in TI materials (23, 24). Nevertheless, theoretical studies of dopant effects (1–6) have raised several fundamental issues about the atomic-scale phenomenology of ferromagnetic TIs that can be resolved only by direct electronic structure visualization experiments. First, what effect (if any) does the random distribution of dopant atoms have on the formation and homogeneity of the ferromagnetic state? Second, and perhaps most importantly, what are the consequences of any nanoscale disorder in the ferromagnetism for spatial arrangements of the Dirac-mass gap? Finally, if such Dirac-mass disorder existed, how would it influence the all-important transport characteristics of the surface states? A detailed atomic-scale understanding of the actual physical arrangements of ferromagnetic TI surface states in the presence of magnetic dopant atoms is required to address these issues.

Magnetic Dopant-Atom–Induced Dirac-Mass Disorder

Theoretical models (1–6) for the surface physics of a doped TI hypothesize that magnetic interactions between pairs of dopant atoms are mediated by the topological surface states (SI Text, section 1). Elementary models estimate (1) the effective z component of the magnetic field at dopant site i as

$$B_{z,i}\left(\mathit{r}\right)={\displaystyle \sum }_j{\Phi }_Z\left(\mathit{r}-{\mathit{r}}_{\mathit{j}}\right)S_{z,j},$$ [1A]

where r_j are the dopant-atom locations and

$${\Phi }_Z\left(\mathit{r}\right)=-\frac{J^{\ast 2}\left(F_{+}\left(k_{F}r\right)+F_{-}\left(k_{F}r\right)\right)}{\hslash v{r}^3}.$$ [1B]

Here k_F is the Fermi wavevector of the topological surface states, $F_{+(-)}\left(x_F\right)={\displaystyle {\int }_0^{x_F\left(x_c\right)}\left(xdx/2\pi \right)}{\displaystyle {\int }_{x_F}^{x_c}\left(x^{\prime }d{x}^{\prime }/2\pi \right)}\left(1/\left(+(-)x-x^{\prime }\right)\right)\left[J_0\left(x\right)J_0\left(x^{\prime }\right)-(+)J_1\left(x\right)J_1\left(x^{\prime }\right)\right]$, where $J_n\left(x\right)$ is the Bessel function, and $x_c=k_{c}r$ effectuates a high cutoff momentum $k_c$. In such cases, the distribution of z-axis magnetization $M_z\left(\mathit{r}\right)$ should become heterogeneous due to random fluctuations in spatial density $n\left(\mathit{r}\right)$ of dopant atoms. The most important consequences of such spatial variations in $M_z\left(\mathit{r}\right)$, whatever their microscopic origin, include a heterogeneous Dirac-mass gap

$$\Delta \left(\mathit{r}\right)=\frac{J^{\ast }{M}_z\left(\mathit{r}\right)}{2{\mu }_B}$$ [2]

(SI Text, section 1) and thus a spatially disordered dispersion of the surface states $E_{\pm }\left(\mathit{r}\right)=E_D\left(\mathit{r}\right)\pm \sqrt{{\left(\hslash v\right)}^2{k}^2+\Delta {\left(\mathit{r}\right)}^2}$. Although excellent progress has been achieved in visualization of electronic structure in ferromagnetic TI compounds (25–27), the atomic-scale effects of magnetic dopant atoms on the Dirac-mass gap and on its contingent physics have not yet been determined.

Experimental Methods

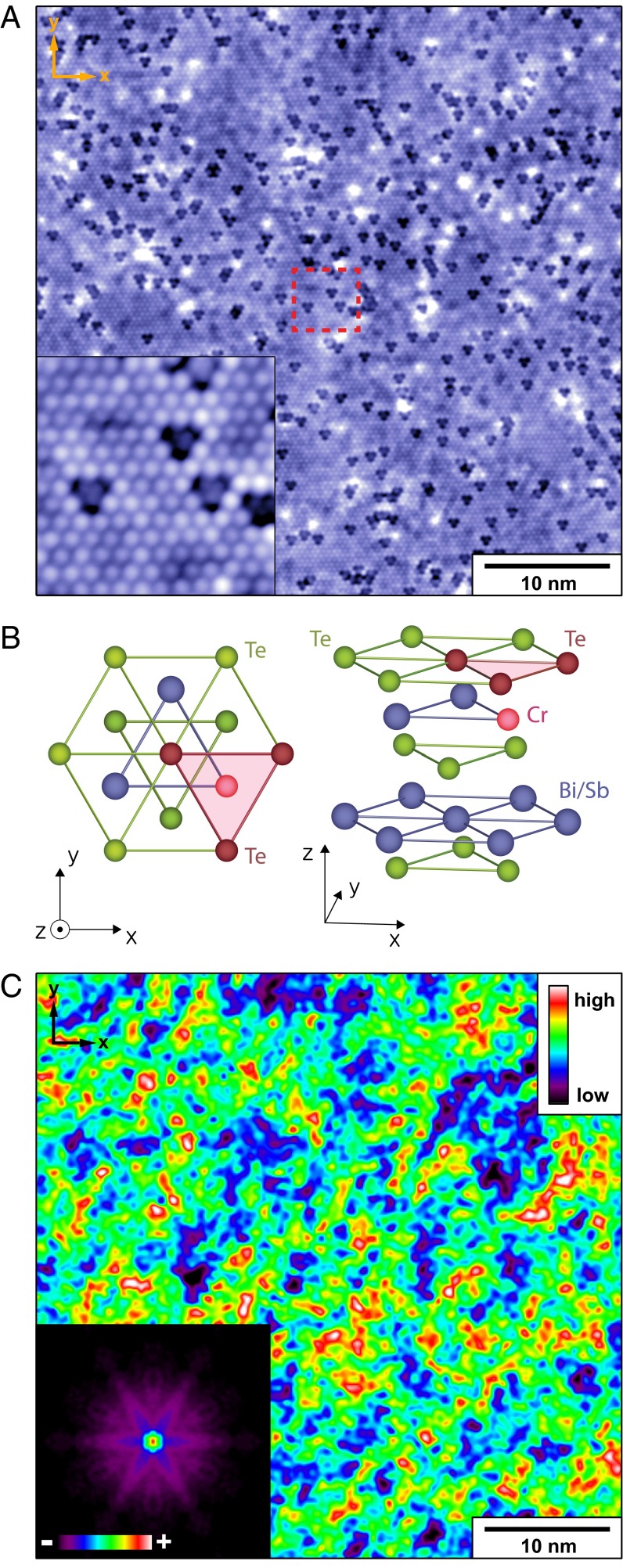
To explore these issues, we use spectroscopic imaging scanning tunneling microscopy (28) (SI-STM) to study Cr_0.08(Bi_0.1Sb_0.9)_1.92Te₃ (CBST) single crystals. These materials are chosen because they are indeed ferromagnetic (29, 30), they exhibit topological surface states with a Dirac point E_D near the Fermi energy E_F (31), and they exhibit the QAHE (19–22). Our SI-STM experiments are carried out in cryogenic ultrahigh vacuum at T = 4.5 K, well below the measured T_C ∼ 18 K bulk ferromagnetic phase transition in these samples. The technique consists of measuring the differential tunneling conductance $dI/dV\left(\mathit{r},E=eV\right)\equiv g\left(\mathit{r},E\right)$ as a function of both location r and electron energy E; it is unique in capability to access simultaneously the r-space and k-space electronic structure for states both above and below the Fermi energy (28). In Fig. 1A we show a typical topographic image T(r) of the Te termination surface of our CBST samples. Fig. 1B is a schematic of the relevant unit cell and identifies the Cr atom substitutional site (pink) in the Bi-Sb layer just beneath the Te surface; we see that it occurs in the center of a triangle of surface Te atoms. This allows the location of each Cr dopant atom adjacent to the termination layer, Cr(r), to be identified experimentally as the center of a dark triangle in Fig. 1A and all equivalent T(r). The measured spatial density of such sites in our samples is 0.23 nm⁻², indicating ∼8% Cr/Bi substitutions (SI Text, section 2). Fig. 1C then shows an image of the differential conductance $g\left(\mathit{r},E=-50\hspace{0.5em}\text{meV}\right)$ measured in the same field of view (FOV) as Fig. 1A, with Fig. 1C, Inset showing its spectral-density Fourier transform g(q, E), which exemplifies the surface-state quasiparticle scattering interference (QPI) phenomena (32–34).

Fig. 1.

Cr dopant-atom locations at the TI surface. (A) Topographic image T(r) of Cr_0.08(Bi_0.1Sb_0.9)_1.92Te₃ surface in a 47 × 47-nm² field of view (FOV). Inset shows zoomed-in topographic image of red dashed-box area. Both images were measured at 10 pA/−200 meV. A single Cr dopant atom exists substituted at the Bi/Sb site at the symmetry point of every dark triangle in T(r) as discussed in B. (B) Schematic of the crystal structure of Cr_x(Bi_0.1Sb_0.9)_2-xTe₃. Each substitutional Cr atom is located at a Bi/Sb site at the symmetry point of a triangle of surface Te atoms (A). (C) Measured differential conductance g(r, E = −50 meV) in the same FOV as A. Inset shows spectral-density Fourier transform of the r-space differential conductance image showing the q-space signature of Friedel oscillations due to scattering interference of the surface-state electrons.

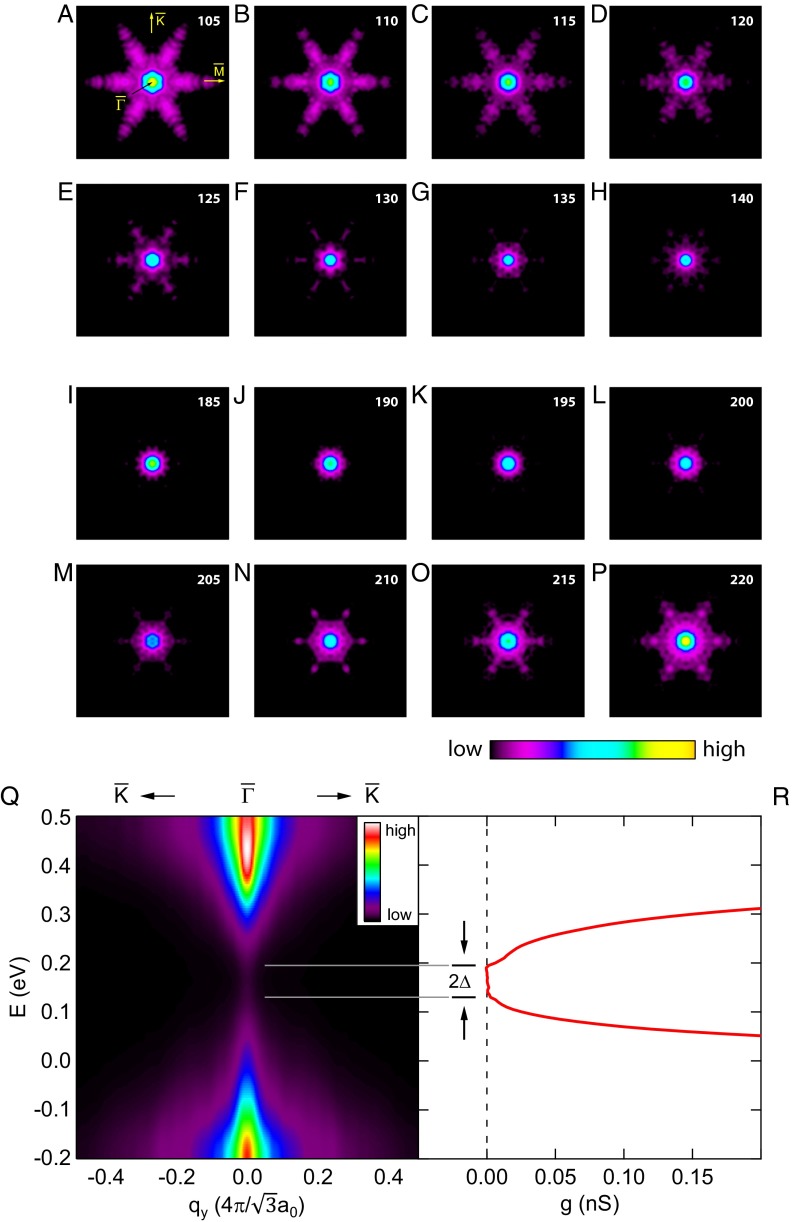
Here we introduce the QPI technique to the study of ferromagnetically gapped TI surface states, by simultaneously imaging the tunnel current $I\left(\mathit{r},E=eV\right)$ and $g\left(\mathit{r},E\right)$. We use this approach because the density of surface electronic states $N\left(\mathit{r},E\right)$ is related to the differential tunneling conductance as $g\left(\mathit{r},E\right)\propto \left[e{I}_s/{\displaystyle {\int }_0^{e{V}_s}N\left(\mathit{r},E^{\prime }\right)d{E}^{\prime }}\right]N\left(\mathit{r},E\right)$ (I_s and V_s are arbitrary parameters). Thus, valid determination of $N\left(\mathit{r},E\right)$ is not possible because the denominator ${\displaystyle {\int }_0^{e{V}_s}N\left(\mathit{r},E^{\prime }\right)d{E}^{\prime }}$ is unknown and heterogeneous (ref. 28 and below). We mitigate the consequent and serious systematic errors by using the function $K\left(\mathit{r},E\right)=\langle I\left(E\right)\rangle g\left(\mathit{r},E\right)/I\left(\mathit{r},E\right)$ because $I^{-1}\left(\mathit{r},E\right)\propto {\displaystyle {\int }_0^{e{V}_s}N\left(\mathit{r},E^{\prime }\right)d{E}^{\prime }}$ and $\langle I\left(E\right)\rangle$ provides normalization from the spatially averaged current. Then, when $g\left(\mathit{r},E\right)\hspace{0.17em}\text{and}\hspace{0.17em}I\left(\mathit{r},E\right)$ are measured at T = 4.5 K in the FOV of Fig. 1A and $K\left(\mathit{q},E\right)$, the spectral-density Fourier transform of $K\left(\mathit{r},E\right)$, is determined (SI Text, section 3). Analyzing these QPI data for E < E_F, we find dispersion of the surface states consistent with angle resolved photoemission spectroscopy (ARPES) studies of the same samples (SI Text, section 3). Moreover, above E_F the QPI data reveal vividly the appearance of the Dirac-mass gap starting at $E\approx 130$ meV (SI Text, section 3). Fig. 2 A–P illustrates this result directly, using a sequence of typical $K\left(\mathit{q},E\right)$ images that span the energy range 105 meV < E < 220 meV. With increasing E, the surface-state QPI signature evolves smoothly and with diminishing |q| until q = 0 is reached just above $E\approx 130\hspace{0.5em}\text{meV}$ (Fig. 2G). At this point, the surface-state QPI disappear, leaving only noise near q = 0. Just below $E\approx 200\hspace{0.5em}\text{meV}$, the surface-state QPI signatures reappear once again, emerging from q = 0 (Fig. 2M). In Fig. 2Q we show the measured ${K\left(q_y,E\right)|}_{q_x=0}$ from the same $K\left(\mathit{q},E\right)$ data revealing directly how the QPI dispersion evolves toward q = 0 for $E<130\hspace{0.5em}\text{meV}$, disappears at $130\hspace{0.5em}\text{meV}<E<200\hspace{0.5em}\text{meV}$, and then reappears to evolve away from q = 0 at $E>200\hspace{0.5em}\text{meV}$. This situation is very well described by two surface-state bands $E_{\pm }\left(\mathit{k}\right)=E_D\pm \sqrt{{\left(\hslash v\right)}^2{k}^2+{\mathrm{\Delta }}^2}$, meaning that the energy range devoid of QPI between the two band edges is twice the Dirac-mass gap Δ. For comparison, the spatially averaged differential conductance $\overline{g}\left(E\right)$ in the same FOV is shown in Fig. 2R. Its magnitude becomes indistinguishable from zero between $130\hspace{0.5em}\text{meV}<E<200\hspace{0.5em}\text{meV}$, demonstrating independently that the Dirac-mass gap Δ has opened in this range as indicated by the arrows spanning 2Δ. Thus, the magnitude of Δ can be detected both directly and locally by measuring half the energy range where tunneling conductance is indistinguishable from zero in g(r, E) (e.g., black arrows in Fig. 2R). These, and equivalent observations in multiple samples, also demonstrate that the ungapped Dirac point is somewhere near E_D = +150 meV. More significantly they also show directly that the Dirac-mass gap magnitude is Δ ∼ 30 meV and that the bulk states also seem gapped because no tunneling is detected at T = 4.5 K in this energy range. Thus, as widely reported (19–22, 29–31), the Cr_x(Bi_ySb_1-y)_2-xTe₃ materials appear to be excellent candidates to exhibit the exotic new phenomena predicted for the gapped surface states of a TI.

Fig. 2.

Measuring Dirac-mass gap from both tunneling spectrum and QPI. (A–P) Quasiparticle interference of TI surface states is visualized as a function of energy using the spectral-density $K\left(\mathit{q},E\right)$, the Fourier transform of $K\left(\mathit{r},E\right)=\langle I\left(E\right)\rangle g\left(\mathit{r},E\right)/I\left(\mathit{r},E\right)$ [for more details including a movie of K(r,E) see SI Text, section 3]. Here we see directly the disappearance of the surface-state QPI in an energy window between 130 meV and 200 meV. The white number in the top right corner represents the measured energy in unit of meV. (Q) Measured dispersions in quasiparticle interference of the TI surface states is plotted using $K(q_x=0,q_y,E)$, the E–q line cut along $\overline{\mathrm{\Gamma }}-\overline{K}$. Here again the evolution of scattering interference signature of surface states to reach q = 0 at ∼130 meV, followed by their disappearance, and the reappearance at and dispersion away from q = 0 near E ∼ 200 meV, is manifest. The Dirac gap magnitude Δ is half the energy range between the two q = 0 tips of the surface-state bands, as indicated by fine grey lines. (R) $\overline{g}\left(E\right)$, the spatially averaged tunneling conductance, simultaneously measured with Q showing that conductance becomes indistinguishable from zero within the same energy window as in Q. Again, this indicates that the Dirac gap magnitude Δ is half the energy range between points at which conductance disappears/reappears, as indicated by black arrows.

Visualization of the Dirac-Mass Gap

Next we introduce the Dirac-mass “gapmap” technique designed to measure spatial arrangements of $\mathrm{\Delta }\left(\mathit{r}\right)$ and apply it throughout the FOV of Fig. 1A. Atomically resolved $g\left(\mathit{r},E\right)$ data are measured at 4.5 K and, for each pixel location r, we define a mask function $f\left(\mathit{r},E\right)$ = 1 if $g\left(\mathit{r},E\right)<$ 40 pS (the tunnel conductance noise floor) and $f\left(\mathit{r},E\right)$ = 0 otherwise. This determines the value of Dirac-mass gap $\mathrm{\Delta }\left(\mathit{r}\right)=\left(1/2\right){\displaystyle \int f\left(\mathit{r},E\right)dE}$. Fig. 3A shows a sequence of spectra, $\overline{g}(\Delta )$, each representing the average of all spectra measured to have the same value of Δ. Each $\overline{g}(\Delta )$ is vertically offset by the same amount for clarity; the zero of conductance in each case is indicated by a fine horizontal line. The value of 2Δ is then indicated for each $\overline{g}(\Delta )$ by the energy span between the pairs of arrows in Fig. 3A. Fig. 3B shows the histogram of all values of $\mathrm{\Delta }\left(\mathit{r}\right)$ detected in the FOV of Fig. 1A and labels each value of Δ, using a color scale. The distribution of $\mathrm{\Delta }\left(\mathit{r}\right)$ is centered near Δ = 28 meV and exhibits a wide but approximately normal distribution. Finally, Fig. 3C shows the atomically resolved spatial arrangements of $\mathrm{\Delta }\left(\mathit{r}\right)$ in a Dirac-mass gapmap. The autocorrelation width of this image is 1.24 nm (SI Text, section 4), indicating that there are a wide variety of nanodomains of like Δ, each with radius near 0.62 nm. Due to coalescence, of course, many regions of similar Δ are significantly larger (Fig. 3C).

Fig. 3.

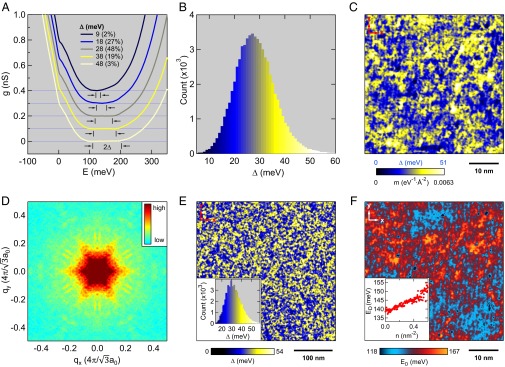
Dirac-mass gapmap. (A) Measured conductance spectra, $\overline{g}(\Delta )$, each representing the average of all spectra with the same value of Δ from the FOV of Fig. 1A. Each $\overline{g}(\Delta )$ is offset vertically for clarity and the zero of conductance is shown by a fine horizontal line. The value 2Δ in each $\overline{g}(\Delta )$ is the energy span between the pairs of arrows. (B) Histogram of the $\Delta \left(\mathit{r}\right)$ measured in the FOV of Fig. 1A. (C) Dirac-mass gapmap $\Delta \left(\mathit{r}\right)$ [or Dirac-mass map $\text{m}\left(\mathit{r}\right)$] extracted from $g(\mathit{r},E)$ measured in the FOV of Fig. 1A. This is typical of maps made using similar parameters on multiple samples of this compound. Tip-induced band bending effects have been systematically ruled out by checking that these results are independent of the tip elevation. (D) Fourier transform of the Dirac-mass gap map $\Delta \left(\mathit{r}\right)$ from the FOV of Fig. 1A. The q-space anisotropy in $\Delta \left(\mathit{q}\right)$ is as would be expected due to the anisotropic values of k_F in the TI of the surface states. (E) Dirac-mass gap $\mathrm{\Delta }\left(\mathit{r}\right)$ measured in the 360 × 360-nm² FOV much larger than the map in C. Inset shows the histogram of $\mathrm{\Delta }\left(\mathit{r}\right)$. (F) Map of estimated ungapped Dirac-point energy (gap center), $E_D\left(\mathit{r}\right)$ $\left(={\displaystyle \int f\left(\mathit{r},E\right)\mathrm{\cdot }EdE}/{\displaystyle \int f\left(\mathit{r},E\right)dE}\right)$ obtained in the same FOV as C, where $f(\mathit{r},E)$ is the gap mask function defined in the text. Inset shows each data point represents the average value of gap center $E_D$ over all of the regions having the same value of Cr density n.

Interplay of Surface States and Ferromagnetism

Because E_F is ∼150 meV below the implied Dirac point, the hexagonal warping of the Fermi surface (e.g., Fig. 1C and SI Text, section 3) should play a significant role, because the magnitude of k_F becomes a function of direction in momentum space. A rotational anisotropy in the Dirac-mass gap would then be expected from models similar to Eq. 1, if dopant atoms interact magnetically via the TI surface states. Taking the Fourier transform of the measured $\mathrm{\Delta }\left(\mathit{r}\right)$ (Fig. 3C), this is what we detect (Fig. 3D), with the lobes in $\mathrm{\Delta }$(q) oriented in the expected directions. When viewed in a much larger field of view (Fig. 3E), the $\mathrm{\Delta }\left(\mathit{r}\right)$ remain rather uniformly distributed with no extreme outliers in the mass gap fluctuations. Moreover, we detect a small energy shift of each local Dirac point E_D(r) from analysis of the g(r, E) spectra (SI Text, section 5). This effect varies weakly in space (Fig. 3F) with fluctuations of E_D of up to ∼10 meV (Fig. 3F, Inset). Indeed, by comparing the q-space geometry from QPI measurements at E = 0 and E = +10 mV we can roughly estimate that (SI Text, section 5) at 8% substitution each Cr atom contributes ∼0.01 holes to the TI surface-state band. These miniscule dopant-induced surface-state band shifts are expected if Cr is an isovalent dopant and do not alter the Fermi surface geometry appreciably. Therefore, they negligibly impact the primary electronic processes leading to the Dirac-mass gap whose characteristic energy range is at least five times greater. Overall, the dominant revelation in these data is how strikingly disordered at the nanoscale (Fig. 3) are the Dirac-mass gaps of these doped ferromagnetic TIs.

Atomic-Scale Influence of the Cr Dopant Atoms

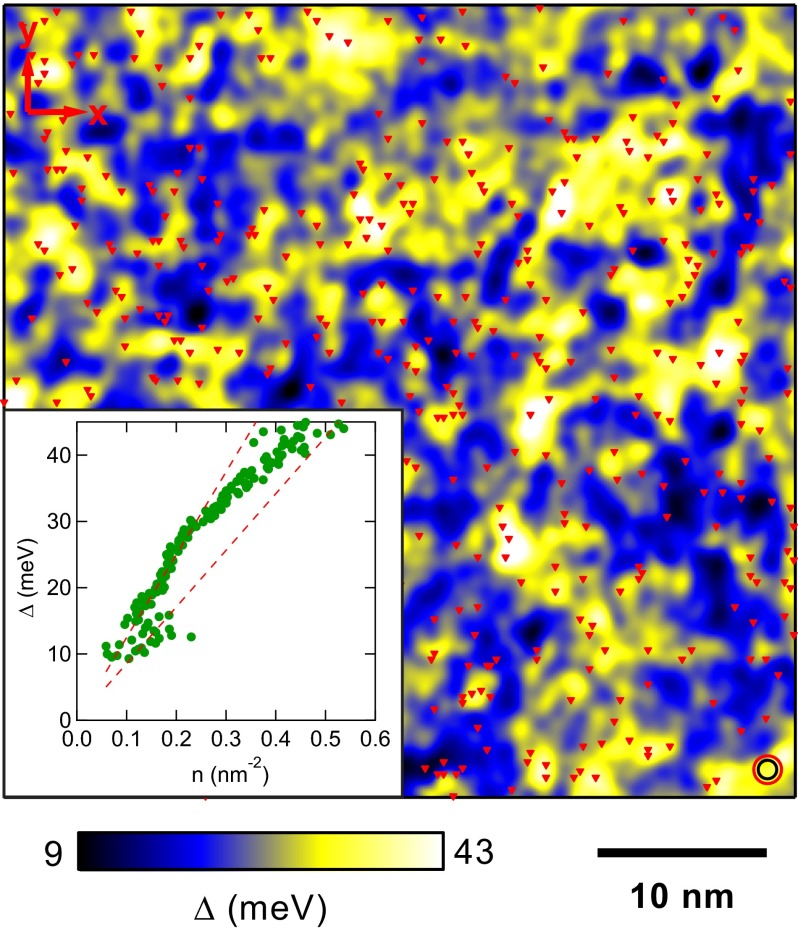
Could the type of Dirac-mass disorder uncovered in Fig. 3 C and E be driven by local variations of $M_z\left(\mathit{r}\right)$ due to deviations in $n\left(\mathit{r}\right)$ arising from the random distribution of the Cr dopant atoms? To study this issue, we first identify the location of each Cr atom $Cr\left(\mathit{r}\right)=\delta \left(\mathit{r}-{\mathit{r}}_{Cr}\right)$, where ${\mathit{r}}_{Cr}$ are the centers of all dark triangles in Fig. 1A. The results are indicated by the red triangles in Fig. 4. Next, to establish a local measure of areal density, $n\left(\mathit{r}\right)$, it is necessary to define a distance scale (SI Text, section 4). To do so we define two images $n\left(\mathit{r},\xi \right)$ and $\Delta \left(\mathit{r},\zeta \right)$, where ξ(ζ) is the Gaussian correlation length of $n\left(\mathit{r}\right)\left(\Delta \left(\mathit{r}\right)\right)$ images. Then we identify the maximum in the normalized cross-correlation of these two processed images $n\left(\mathit{r},\xi \right)$ : $\Delta \left(\mathit{r},\zeta \right)$ as a function of both ξ and ζ. We find that it occurs at ξ ∼ 0.82 ± 0.1 nm, the empirical radius of influence of each Cr atom at which their arrangements correspond maximally to the Dirac-mass arrangements in $\Delta \left(\mathit{r}\right)$, whereas for $\Delta \left(\mathit{r}\right)$ this occurs at ζ ∼ 0.55 ± 0.1 nm. Notwithstanding which microscopic interactions drive the surface ferromagnetism in CBST, we find that the distribution of Cr atoms $n\left(\mathit{r}\right)$ is correlated manifestly with the $\Delta \left(\mathit{r}\right)$. One can see this directly in Fig. 4, which is a representative subset of Fig. 3C in which every Cr site is represented by a red triangle. Furthermore, Fig. 4, Inset shows the plot of the average value of $\Delta \left(\mathit{r}\right)$ associated with each value of $n\left(\mathit{r}\right)$ and reveals a quasi-linear relationship between local Dirac-mass gap and local Cr density. Indeed, the slope of $\Delta \left(\mathit{r}\right)=\lambda \mathrm{\cdot }n\left(\mathit{r}\right)$ allows the surface-state–dopant interaction energy scale (e.g., Eq. 2) to be measured directly. Thus, for Cr-doped CBST, we find that J* = 145 ± 25 meV·nm² everywhere, despite strong fluctuations in $n\left(\mathit{r}\right)$ (Figs. 1A and 4).

Fig. 4.

Atomic-scale measurements of interaction strength of surface states with magnetic dopant atoms. Shown above is a measured Dirac-mass gap map $\Delta (\mathit{r},\zeta =0.55\hspace{0.5em}\text{nm})$ with Gaussian smoothing length ζ, overlaid with Cr locations measured from Fig. 1A (red triangles). Cr atoms are observed to be positioned with high probability in the larger gap areas (yellow), but rarely in the smaller gap areas (blue). The other fainter features in topography (white) are shown not to occur at Bi/Sb substitutional sites, so we do not assign them as magnetic dopant atoms. Red and black circles on the right bottom corner indicate the correlation radii ξ = 0.82 nm and ζ = 0.55 nm, respectively. (Inset) Each data point represents the average value of Dirac mass gap over all of the regions having the same value of Cr density n. The resulting slope of best linear fit yields J* = 145 meV·nm². This is to our knowledge the first atomic-scale measurement of the interaction strength of surface states with magnetic dopant atoms in a ferromagnetic TI. The uncertainty represented by two dashed lines is not statistical but comes from the systematic uncertainty in magnitude of S_z, which we take to be 20%.

Conclusions and Discussion

To summarize, by studying the recently developed material Cr_x(Bi_ySb_1-y)_2-xTe₃ we provide to our knowledge the first simultaneous visualization of the location of magnetic dopant atoms and the Dirac-mass gap in a ferromagnetic TI. By using QPI imaging of the TI surface states for E > E_F, we detect the Dirac mass gap of magnitude Δ ∼ 30 meV with a hidden Dirac point at E_D ∼ 150 meV (Fig. 2). Imaging $\Delta \left(\mathit{r}\right)$ reveals directly (Figs. 3 C and E and 4) that its nanoscale disorder is intense. We then demonstrate that the $\Delta \left(\mathit{r}\right)$ disorder is robustly correlated with fluctuations in the areal density $n\left(\mathit{r}\right)$ of magnetic Cr atoms in the crystal termination layer (Fig. 4). Moreover, the miniscule scale of dopant-induced surface-state band shifts (Fig. 3F and SI Text, section 5) shows that $\Delta \left(\mathit{r}\right)$ fluctuations are not due to chemical disorder. Conversely, we confirm everywhere the relationship $\mathrm{\Delta }\left(\mathit{r}\right)\propto n\left(\mathit{r}\right)$, a result not inconsistent with surface-state–mediated ferromagnetism (SI Text, section 1). Finally, in the latter context we derive a universal dopant–surface-state interaction energy scale of J* = 145 meV·nm² (Fig. 4) for Cr_0.08(Bi_0.1Sb_0.9)_1.92Te₃.

The Dirac-mass gapmap technique introduced here reveals several new perspectives on the physics of ferromagnetic topological insulators. The key characteristics observed in $\Delta \left(\mathit{r}\right)$ such as its overall magnitude, the spatial correlation of $\mathrm{\Delta }\left(\mathit{r}\right)\hspace{0.17em}\text{with}\hspace{0.5em}n\left(\mathit{r}\right)$ on the ∼1.5-nm scale, the local proportionality $\mathrm{\Delta }\left(\mathit{r}\right)\propto n\left(\mathit{r}\right)$, and the structure of $\mathrm{\Delta }\left(\mathit{q}\right)$ oriented with anisotropic Fermi wavevectors k_F(E = 0) of the surface states are all consistent with Dirac-mass gap opening due to surface-state–mediated ferromagnetism. Moreover, the mysterious QAHE phenomenology (19–22) must now be reconsidered as occurring in the context of extreme Dirac-mass disorder at the nanoscale. Indeed, the chiral states expected at the perimeters of ferromagnetic domains (35) now seem required to navigate through a geometrically complex environment. A key consequence could be that, if FM domain walls percolate (as might be anticipated from Fig. 4), the chiral edges at the sample boundary can hybridize through the percolating internal edges at the domain walls and the QAHE conductance lose its quantization because the sample is situated at the critical point of the quantum Hall plateau transition. Therefore, to reliably achieve all of the exotic physics expected of time-reversal symmetry breaking TI materials (7–18), it now appears that an approach to controlling the severe dopant-induced Dirac-mass gap disorder will first need to be identified. Application of techniques initiated here provides a promising new approach to this important challenge.