Exploring the speed and performance of molecular replacement with AMPLE using QUARK ab initio protein models

Two ab initio modelling programs solve complementary sets of targets, enhancing the success of AMPLE with small proteins.

Abstract

AMPLE clusters and truncates ab initio protein structure predictions, producing search models for molecular replacement. Here, an interesting degree of complementarity is shown between targets solved using the different ab initio modelling programs QUARK and ROSETTA. Search models derived from either program collectively solve almost all of the all-helical targets in the test set. Initial solutions produced by Phaser after only 5 min perform surprisingly well, improving the prospects for in situ structure solution by AMPLE during synchrotron visits. Taken together, the results show the potential for AMPLE to run more quickly and successfully solve more targets than previously suspected.

1. Introduction  

Molecular replacement (MR) is by far the most popular route to the solution of the phase problem, accounting for over 70% of the structures deposited in the Protein Data Bank (PDB; Rose et al., 2012 ▶) in recent years. In MR, phasing information is derived by placing a search model in the unit cell of the target to approximate its crystal lattice (Rossmann & Blow, 1962 ▶). The search model is typically an existing structure that is homologous and thus structurally resembles the target or an edited version thereof. Alternatively, homology modelling may produce an explicit prediction of the target structure for use as a search model. Either way, truly novel folds, that have not previously been structurally characterized, are generally rendered intractable for MR.

Key to broadening the applicability of MR is the exploitation of modelling approaches that can deal with targets whose folds are not, or are only poorly, represented in the PDB. One route is to model and place small fragments, such as isolated α-helices or characteristic motifs, whose local structure can be reliably predicted irrespective of the overall fold context (Rodríguez et al., 2009 ▶, 2012 ▶; Sammito et al., 2013 ▶). This approach, as implemented in ARCIMBOLDO, has achieved conspicuous successes but requires very significant computing resources. A second route is to use ab initio protein models as delivered by programs such as ROSETTA (Shortle et al., 1998 ▶; Simons et al., 1997 ▶, 1999 ▶), I-TASSER (Zhang, 2008 ▶; Roy et al., 2010 ▶; Wu et al., 2007 ▶) or QUARK (Xu & Zhang, 2012 ▶). These programs attempt to predict the entire structure of the target and generally function in two steps. Firstly, a rapid, fragment-assembly step operating on a reduced protein representation produces so-called ‘decoys’. Clusters of decoys represent candidate fold predictions which can then be subjected to a second step, an all-atom refinement which entails much greater CPU demands. All-atom ab initio predictions have succeeded in MR (Qian et al., 2007 ▶; Das & Baker, 2009 ▶), but their computational needs prevent broader adoption. As an alternative, we have explored the use of the more quickly obtained decoys as search models. Using our method for decoy clustering and graded truncation, we showed that decoys solve more than 40% of a nonredundant set of small protein structures (Bibby et al., 2012 ▶).

Ab initio methods for protein structure prediction are an active area of research, with iterative fragment-based approaches (Zhang & Skolnick, 2013 ▶) and new contact-based methods (Marks et al., 2012 ▶) both pushing the size limit of tractable proteins. Here, we explore models produced by QUARK (Xu & Zhang, 2012 ▶), a new fragment-based approach that differs from ROSETTA in several important ways. For example, QUARK uses fragments of a size range of 1–20 residues, while ROSETTA typically employs only fragments of three or nine residues. Furthermore, the force field used differs, with that of QUARK combining both physical and knowledge-based energy terms. Finally, and of particular note, its novel collection of contacts based on distance profiles helps to pack the medium-to-long-range residue interactions (Xu & Zhang, 2013 ▶). Recent assessments have shown QUARK to be one of the best-performing methods in its class (Kinch et al., 2011 ▶; Tai et al., 2014 ▶). We find that QUARK solves an overlapping but distinctly complementary set of targets compared with previous work using ROSETTA (Bibby et al., 2012 ▶). We also demonstrate that more recent versions of Phaser (McCoy et al., 2005 ▶, 2007 ▶; Storoni et al., 2004 ▶) and SHELXE (Sheldrick, 2008 ▶; Usón et al., 2007 ▶; Thorn & Sheldrick, 2013 ▶), two key components of the AMPLE pipeline, produce significantly improved results. Finally, and unexpectedly, the imposition of a 5 min limit on Phaser degrades the success rate by less than 10%.

2. Materials and methods  

2.1. Materials  

For ease of comparison with previous results, we used our previously published set of 295 nonredundant protein targets (Bibby et al., 2012 ▶; Supplementary Table S1). The selection criteria for these were a length of 40–120 residues, a resolution of better than 2.2 Å, an absence of bound metal or cofactor and R ≤ 0.25, R _free ≤ 0.35. They were grouped into three classes, all-α, all-β and mixed αβ, as described previously.

2.2. Methods  

For each sequence, QUARK (Xu & Zhang, 2012 ▶) produced 5000 individual structures. In the terminology of ab initio modelling, these low-resolution, rapidly obtained predictions are known as decoys. Briefly, the software first generated a set of structural fragments with lengths from one to 20 amino acids at each position of the query sequence. These fragments were used to assemble the ab initio models by replica-exchange Monte Carlo (REMC) simulations under the guide of a generic, atomic-level knowledge-based force field with consideration of various sequence-specific predicted structural features, including secondary-structure type, solvent accessibility and β-turn propensity. For each query, QUARK ran ten independent REMC simulations starting from different random numbers. In each run, 50 decoys were selected from each of the ten low-temperature trajectories, resulting in 5000 decoys. The decoys lacked the explicit side chains that a full, CPU-intensive modelling would add. PDB structures with a sequence identity of >30% to the target or detectable by PSI-BLAST (a criterion used by most of the ab initio folding benchmark tests; Zhang et al., 2003 ▶; Simons et al., 2001 ▶) were excluded from the fragment library.

Processing of decoys into search models used the AMPLE pipeline (Bibby et al., 2012 ▶). Briefly, decoys were clustered using SPICKER (Zhang & Skolnick, 2004 ▶) and centroid structures representing the three largest clusters were used to generate ensembles containing structural neighbours. Side chains were added to the ensembles using SCRWL (Canutescu et al., 2003 ▶; Krivov et al., 2009 ▶). The structural diversity within each ensemble predicts the deviation from the true structure (Qian et al., 2007 ▶; Bibby et al., 2012 ▶), and therefore the variance along the chain was quantified with THESEUS (Theobald & Wuttke, 2006 ▶) and used to derive up to 20 progressively more truncated versions of each ensemble. A sub-clustering step, collecting up to 30 near-centroid structures at 1, 2 and 3 Å r.m.s.d. thresholds, produced more structurally homogeneous ensembles from these results. After treatment of side chains in three different ways (all retained; only more easily predicted side chains retained and others trimmed to polyalanine; all trimmed to polyalanine) these subclusters became the set of search models. Hundreds of distinct search models may be produced for a single target. They are dealt with by MrBUMP (Keegan & Winn, 2008 ▶). In this work, only Phaser (McCoy et al., 2005 ▶, 2007 ▶; Storoni et al., 2004 ▶) was used for MR solution. Automated density modification and main-chain tracing with SHELXE (Sheldrick, 2008 ▶; Usón et al., 2007 ▶; Thorn & Sheldrick, 2013 ▶) was used to detect successful solutions as having a CC value of ≥25 and a mean traced chain-fragment length of ≥10. For Phaser, default parameters were used with the exception of the estimated r.m.s.d. error (see below). For SHELXE, the following options were used: 15 cycles of autotracing (-a15), searching for α-helices (-q), pruning for optimization of the CC for the input model (-o), the time factor for the helix and peptide search (-t3) and the ‘free-lunch’ option to add missing data up to 1.0 Å resolution if the data resolution was 1.8 Å or better (-e1.0). All other options were set to their default values. Mean phase error (MPE) values were calculated using CPHASEMATCH from the CCP4 suite (Winn et al., 2011 ▶). Here, focusing on overall success rates, AMPLE terminated after finding the first success.

For comparison with published data, QUARK-derived search models were run with Phaser 2.3.0 and SHELXE 2012 (Run 1). The estimated r.m.s.d. error of the search models was set to 0.1 Å, as previously (Bibby et al., 2012 ▶), or to 1.2 Å (Run 2 alone). QUARK-derived search models were also run with Phaser 2.5.4 and SHELXE 2013 (Run 3). Since MR is typically the slowest step in AMPLE, a requested time limit of 5 min for Phaser (KILL TIME 300 flag) was also tested (Run 4). In practice, since Phaser is only terminated at certain points in the code, this most commonly stops Phaser after 10–20 min.

3. Results and discussion  

3.1. Overall performance of QUARK models  

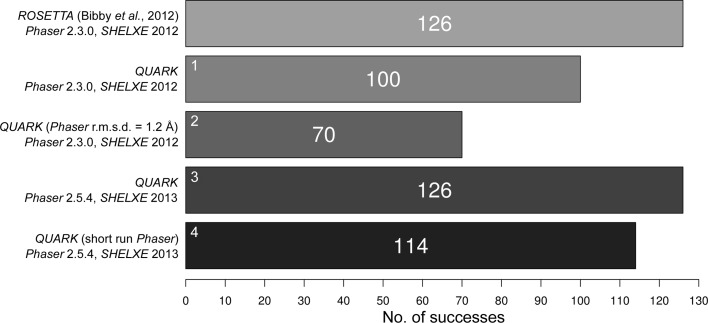
ROSETTA-derived search models processed with Phaser previously solved 126 of the 295 targets. The result for the QUARK set, using the same Phaser and SHELXE versions and operating parameters, is 100/295 (Run 1). As previously (Bibby et al., 2012 ▶), when producing the QUARK models homologous fragments were excluded to treat each target as if it were a novel fold. For comparison we also tested providing Phaser with a 1.2 Å estimated r.m.s. error in the search models (Run 2), as opposed to the 0.1 Å value employed in Run 1. This dramatically reduced the success rate to 70/295 and thus the value of 0.1 Å was used for all of the remaining runs. We then tested the success of the QUARK models using the latest versions of Phaser and SHELXE (Run 3) and found a steep increase in success to 126 of the 295 cases (Fig. 1 ▶).

Figure 1.

Numbers of targets solved with QUARK-derived search models under various conditions compared with previous results (Bibby et al., 2012 ▶). The small numbers at the top left of the columns indicate the run numbers referred to in the text.

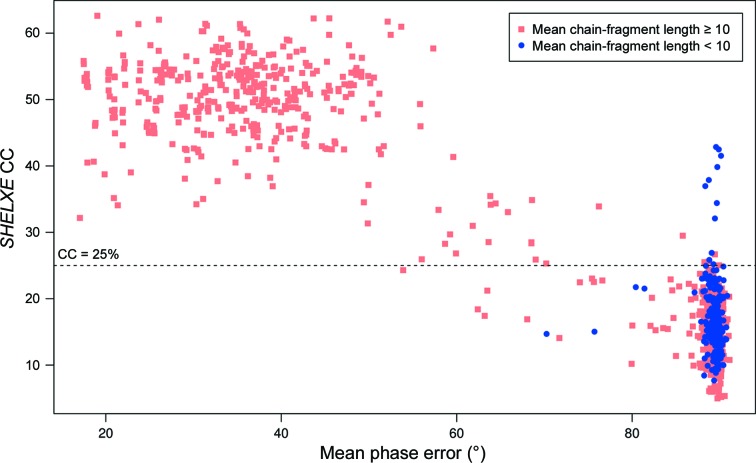
In this work, success is defined by SHELXE (Sheldrick, 2008 ▶; Usón et al., 2007 ▶; Thorn & Sheldrick, 2013 ▶) criteria: a CC value of ≥25 and a mean traced chain-fragment length of ≥10. The work of Thorn & Sheldrick (2013 ▶) suggested that a CC of ≥25 and native data to better than 2.5 Å resolution are invariably indicative of success. Since we are benchmarking against known crystal structures, mean phase errors (MPEs) for successful and failing search models can be calculated (Fig. 2 ▶). The vast majority of the cases defined as successful by the SHELXE criteria indeed have a low MPE. However, in a handful of cases, totalling only seven search models across all of Runs 1–4, solutions classified as successful have an MPE of >75°. Four of these seven false positives relate to PDB entry 2fu2 which, although reported to have a resolution limit of 2.1 Å, diffracted anisotropically to only 2.6 Å in the worst direction. This potentially explains the poor quality of the solutions despite the SHELXE statistics. PDB entry 2qyw (twice) and one search model for PDB entry 3n3f gave the other false positives, and no obvious explanation for the failure of the criteria in these cases is evident. However, three such cases in a set of 1117 (Fig. 2 ▶) is a very low failure rate of the SHELXE-based success criteria and we note that these three cases only marginally passed either the CC or the mean traced chain-length criteria.

Figure 2.

Comparison of SHELXE CC and mean phase error for Runs 1–4 combined. Each point represents a search model and the values are either those of the successful solution or those of the highest failing CC score. Symbols distinguish SHELXE traces that do or do not exceed a mean traced chain-fragment length of 10. In all cases 15 cycles of auto-tracing were invoked in SHELXE. Each cycle included 20 iterations of density modification.

The MPE plot (Fig. 2 ▶) also reveals several targets that have a relatively low MPE but failed to meet the SHELXE scoring criteria. Several cases were examined in more detail: PDB entries 1vjk (MPE = 63.2°) and 2rff (62.4°) from Run 1, 3oiz (63.5°) from Run 3 and 1xak (70°) from Run 4. Of these, 1vjk and 3oiz could be easily improved upon through further cycles of SHELXE, achieving MPE values of 28.7° (CC = 36.1, average chain length = 71) and 36.2° (CC = 47.6, average chain length = 46.5), respectively. The MPE for 2rff and 1vjk could not be improved by further cycles of SHELXE. However, in both cases the partial C^α trace produced by SHELXE was correct when compared with the deposited structure for these targets using the CSYMMATCH program from the CCP4 suite.

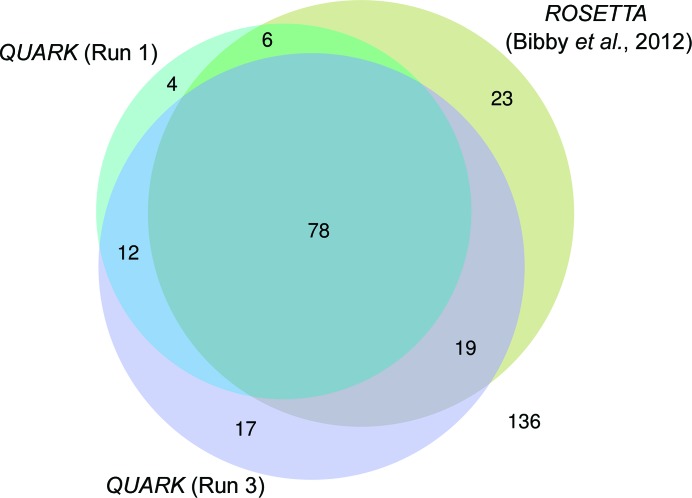
The significant methodological differences between ROSETTA and QUARK led us to assess their performance across target classes and, thereby, their complementarity to increase the overall success rate of AMPLE (Fig. 3 ▶). Using the same versions of Phaser and SHELXE, 16 QUARK (Run 1) and 42 ROSETTA successes were uniquely achieved by each program. Jointly, ROSETTA and QUARK successes amounted to 142 targets (48% of the total, compared with 43% reported for ROSETTA alone). Interestingly, the same QUARK-derived search models were significantly more successful with more recent versions of Phaser and SHELXE (Run 3), solving 29 targets that were not previously solved with ROSETTA. This illustrates how the AMPLE pipeline continuously combines advances in various methodologies to deliver the best performance for automated MR. All runs considered, AMPLE solved 54% of targets, up from 43% with only ROSETTA models (Bibby et al., 2012 ▶).

Figure 3.

Venn diagram illustrating successful solutions using QUARK-derived search models (Runs 1 and 3) compared with previous results (Bibby et al., 2012 ▶).

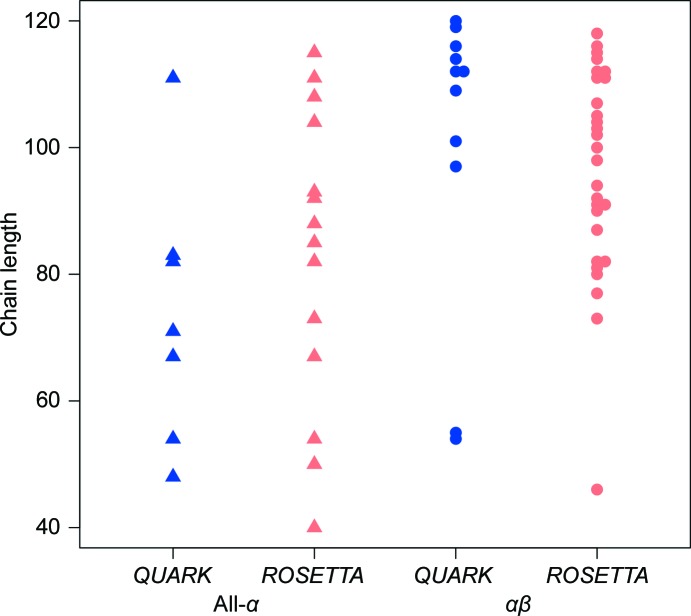
The search models from QUARK predictions performed similarly across secondary-structure classes as the ROSETTA-derived search models (Fig. 4 ▶). In our test set there are 77 all-α, 44 all-β and 174 αβ targets. Particularly noticeable is the poor performance of both programs with all-β targets. The two all-β targets previously solved were also solved by a QUARK-derived search model, but no further successes were added. In contrast, 60 all-α targets solved previously with Phaser (Bibby et al., 2012 ▶) were complemented by four additional successes from QUARK (Run 1), taking the success rate between the two runs to 83%. Remarkably, including Run 3, with modern versions of Phaser and SHELXE, adds a further seven targets solved at least once between Runs 1 and 3 here and previous results (Bibby et al., 2012 ▶): thus, very nearly all of the all-α targets in the set (92%) were solved at least once. In the αβ class, it is notable how the complementarity with QUARK is focused in the larger target-size range above 100 residues or so. As previously (Bibby et al., 2012 ▶), success close to the upper size limit should encourage the application of AMPLE to larger targets.

Figure 4.

Chain lengths and secondary-structure classes of targets uniquely solved using either QUARK-derived (Run 1) or ROSETTA-derived search models (18 and 42 cases, respectively; Bibby et al., 2012 ▶).

Structure solution was achieved across a broad range of diffraction resolutions in the test set. The lowest resolution success was at 2.1 Å (PDB entry 3kw6). The highest resolution target (PDB entry 1ejg, 0.54 Å) was solved in both the original ROSETTA run and in Run 3 here. In general, low solvent content corresponds to higher resolution, and in our tests in all runs the solved structures had a solvent-content fraction ranging from 10.5 to 70.8%. The mean solvent contents for the sets of solutions solved by ROSETTA and each of the QUARK run solutions were around 46%, compared with a mean solvent content in the whole target set of 45%. Thus, in the ranges explored, resolution and solvent content do not appear to have been an influence on solubility in our test set when using ROSETTA-derived or QUARK-derived models. However, a more extensive set of tests over a wider range of resolutions would be needed in order to obtain a clearer picture of the relevance or otherwise of these factors.

12 targets in the test set contained two molecules per asymmetric unit and the rest contained a single molecule. Interestingly, Run 3 was the most successful for these targets, solving 11 of the 12 targets; ROSETTA, Run 1 and Run 4 could solve eight, while Run 2 could solve seven. This suggests that use of the latest versions of Phaser and SHELXE may be particularly important in these cases.

3.2. Results from faster Phaser runs  

The MR step is computationally demanding in AMPLE, accounting for around 33% of the runtime on average. For successful cases in Run 3, runtimes averaged about 48 h per target with pre-calculated QUARK models so, although AMPLE allows parallelization on clusters and multi-core machines, there is nevertheless an incentive to explore ways of speeding up its operation. Phaser regularly outputs its current best result during operation and the KILL TIME flag allows runs to be terminated after a user-specified time. The results show that requesting that Phaser limit the CPU time to 5 min (in practice, up to 30 min; see §2) has a surprisingly small impact on performance (Fig. 1 ▶), with the successfully solved targets only decreasing from 125 to 114. Interestingly, only 103 targets are shared between the long and short Phaser results (Runs 3 and 4, respectively). Supplementary Fig. S1 shows no obvious systematic differences in the characteristics of targets solved exclusively in the shorter run although, unexpectedly, two all-β targets, which are generally harder to solve, were among them. The average time spent running Phaser in successful cases in Run 3 is approximately 16 h per target, with an average of 18 search models tested before a solution is found. In Run 4, the average time spent running Phaser in successful cases drops to 5 h per target, with an average of 25 search models tested before a solution is found. Thus, although more search models have to be tested in the short Phaser run, on average a similar overall per-target success rate is achieved in a distinctly shorter time. More elegant options for limiting Phaser runtimes based on restricting the number of trial orientations or solutions will be explored in future work.

4. Concluding remarks  

The exploitation of unconventional sources of search models is an appealing route to enhancing the applicability of the MR method for structure solution. Given the increased rates of protein crystallization provided by nanodispensing instrumentation and the accelerated speed of data collection at modern synchrotrons, the demand for purely computational phasing approaches that can offer full automation is becoming ever more pressing. These results show that different ab initio methods are complementary in terms of the targets solved in our benchmarking set. Between earlier results and the comparable QUARK results presented here (both Runs 1 and 3 combined), 159 of 295 targets (54%) were solved. Although differing in the software used, it is remarkable that 93% of the all-α targets in the set are demonstrably soluble using either ROSETTA-derived models (Bibby et al., 2012 ▶) or QUARK models (Runs 1 or 3). Thus, almost all small helical proteins can potentially be solved using ab initio models from the current generation of modelling software. Contrariwise, the disappointing results for all-β targets using both ROSETTA and QUARK (5%) suggest there is still a need for significant improvements to ab initio methods for this class of targets. The time-limited Phaser results suggest that an impatient AMPLE user may achieve good results in a shorter time than previously envisaged. Such quick AMPLE runs could, for example, aid in situ structure solution of new folds during diffraction data collection at synchrotrons.

The complementarity of targets solved with ROSETTA or QUARK shows that, computational resources allowing, these programs should be used jointly. AMPLE’s approach requires access to the set of decoy structures rather than the selected fold predictions currently available from some ab initio modelling servers. Currently, ROSETTA is distributed for local use and QUARK is freely available for online server submission, with results including both final models and trajectories of folding decoys. Use of the server eliminates the requirement for AMPLE MR of a local installation of ab initio modelling software. QUARK decoys can be used in AMPLE from the command line using the ‘-quark_models’ flag. Alternatively, the CCP4i interface for AMPLE provides a link to the QUARK server, where users can generate the decoys.tar.gz file that is subsequently employed for search-model generation and MR. A local version of QUARK should become available in the near future.