Responses to Conflicting Stimuli in a Simple Stimulus–Response Pathway

Abstract

The “local bend response” of the medicinal leech (Hirudo verbana) is a stimulus–response pathway that enables the animal to bend away from a pressure stimulus applied anywhere along its body. The neuronal circuitry that supports this behavior has been well described, and its responses to individual stimuli are understood in quantitative detail. We probed the local bend system with pairs of electrical stimuli to sensory neurons that could not logically be interpreted as a single touch to the body wall and used multiple suction electrodes to record simultaneously the responses in large numbers of motor neurons. In all cases, responses lasted much longer than the stimuli that triggered them, implying the presence of some form of positive feedback loop to sustain the response. When stimuli were delivered simultaneously, the resulting motor neuron output could be described as an evenly weighted linear combination of the responses to the constituent stimuli. However, when stimuli were delivered sequentially, the second stimulus had greater impact on the motor neuron output, implying that the positive feedback in the system is not strong enough to render it immune to further input.

Introduction

Sensory systems have traditionally been studied by neuroscientists one modality and one stimulus at a time. This approach has been tremendously successful, yet in nature behaviorally relevant singular events, such as the appearance of a predator or prey, are typically heralded by multiple sensory modalities, and it is also very common for multiple unrelated sensory events to occur with temporal overlap. Of particular interest are sensory conflicts: situations in which multiple simultaneous stimuli would direct the receiver toward contrasting behaviors. Despite recent advances in recording and imaging techniques, establishing the neuronal basis of sensory conflict resolution remains difficult to achieve at the neuronal level in higher animals. Accordingly, little is known about sensory conflict processing at the level of microcircuits. This is unfortunate because one can often learn a lot about the inner workings of a system by exploring the edges of its capabilities (e.g., Marder and Fineberg, 1996).

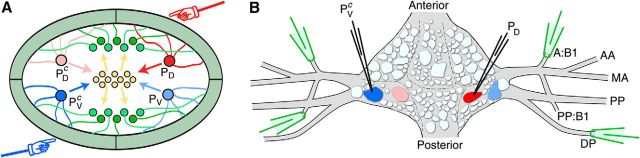
Fortunately, lower animals also encounter sensory conflicts and thus offer opportunities for studying circuits involved in conflict processing in the context of much simpler nervous systems. A particularly attractive example is the local bend circuit in the midbody ganglia of the medicinal leech Hirudo sp., one of the most well-studied examples of a simple stimulus–response pathway (Kristan, 1982; Lockery and Kristan, 1990a, b; Lockery and Sejnowski, 1992; Lewis and Kristan, 1998a, b, c). Consisting chiefly of a three-layer feedforward network of sensory neurons, interneurons, and motorneurons (Fig. 1A), the local bend circuit allows the leech to move away from objects touching any location on its body: Four pressure-sensitive sensory neurons, the P cells, collectively encode location along the body circumference; 17 identified interneurons process this information (Lockery and Kristan, 1990b) and feedforward to 10 identified motor neurons (Kristan, 1982); these command the musculature to accurately move the body away from the stimulus. Traditionally described as a reflex-like response, the local bend response is actually subject to inhibitory control that shapes both the strength of the overall response and its directional tuning (Baca et al., 2008).

Figure 1.

Recording and stimulation. A, Schematic cross section of a leech midbody segment and overview of the local bend circuitry. Four sensory neurons, bilateral P_D and P_V, respond to pressure applied to the body wall (illustrated by hands). The “P” cells project to a set of interneurons (yellow) that in turn project to a set of excitatory and inhibitory motor neurons (green) that innervate the musculature in the body wall. B, Overview of recording and stimulation. A P_D cell and a contralateral P_V cell (labeled P_V^c) are impaled with sharp electrodes used to deliver spike-evoking stimuli. A selection of four nerves is targeted with suction electrodes for simultaneous extracellular recording from the axons of multiple motor neurons. Naming of nerves follows Ort et al. (1974).

Previous work by Lockery and Kristan (1990a) established that leeches react to simultaneous electrical stimuli to adjacent P cells by interpolation of the appropriate responses. This matches the behavioral response to touch to positions intermediate between the centers of the receptive fields of these cells (Lewis and Kristan, 1998b). Evidently, leeches do not appear to perceive a sensory conflict under these conditions. Here, we report how the local bend system reacts to the simultaneous application of two stimuli that would trigger diametrically opposite responses when applied individually: stimulation of one dorsal P cell and the contralateral ventral P cell. In earlier studies, responses to diametrically opposite P cells were not investigated because they were deemed too variable at the level of behavior. We overcome this challenge by analyzing electrical activity recording simultaneously from a large number of motor neurons using nerve suction electrodes.

Materials and Methods

Animals and recording.

Medicinal leeches (Hirudo verbana) were obtained from Niagara Leeches and maintained in standard conditions (Harley et al., 2011). Before dissection, leeches were anesthetized in ice-cold water. Leeches were immobilized on Sylgard (Dow Corning) in a chilled dissection tray and opened along the dorsal midline. After removal of overlying tissue, several nerve roots were exposed surrounding a midbody ganglion (M8-M12) (Kristan, 1982). The ganglion with attached nerve roots was transferred to a Petri dish and pinned down ventral-side up. Suction electrodes were fashioned out of flame-polished microelectrode glass sized for optimal fit to each type of nerve and applied to the nerve ends (Wagenaar et al., 2010). Sharp electrodes (containing 3 M potassium acetate; ∼30 MΩ) were used to penetrate the P cells (Baca et al., 2008). Figure 1B summarizes the recording setup. Extracellular and intracellular signals were amplified with A-M Systems model 1700 and 1600 amplifiers, respectively. P cell identities were confirmed based on their electrophysiological properties. Signals were digitized with a National Instruments data acquisition card and recorded with custom software.

Electrical stimulation.

Action potentials were evoked in P cells by current stimulation: 10-ms-long depolarizing pulses of 0.7–1.5 nA, as low as possible to reliably evoke exactly one action potential in the P cell for each current pulse. Complete stimuli consisted of trains of 2–10 such pulses in a 500 ms window. Commonly, it proved necessary over the course of an experiment to slightly increase the stimulation current to maintain reliability, or to apply a weakly hyperpolarizing holding current between stimuli to keep a P cell from firing additional action potentials following stimulation.

Spike sorting.

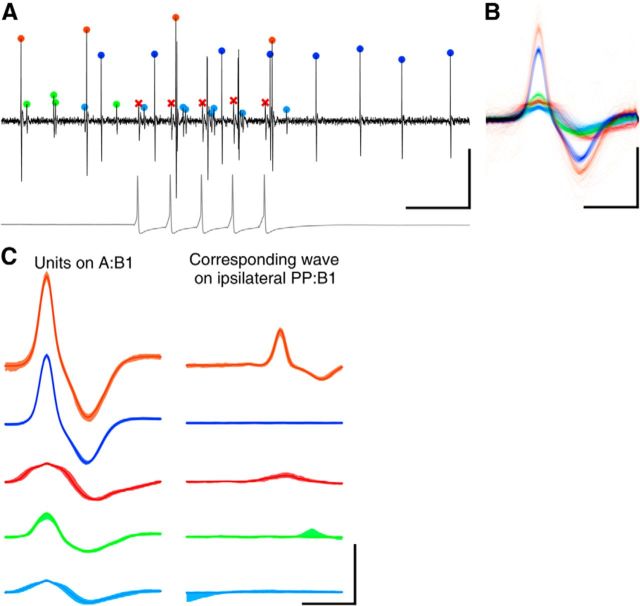
Spikes were extracted from each of the extracellular traces and sorted into putative units using the UltraMegaSort2000 toolbox (Fee et al., 1996; Hill et al., 2011). A typical example of a recorded trace with sorted spikes is shown in Figure 2. Waveforms of some units gradually changed over time. When this happened and the algorithm spuriously split such units into several clusters, these were manually recombined. Because a single-cell body may project axons into multiple nerves, it was common to find matching units in pairs of nerves (Fig. 2C). Such units were identified in the dataset and henceforth considered as a single unit. Units were merged if they exhibited near-perfect spike correspondence (>90%) within a small asymmetric time window, typically 1 or 2 ms. Remaining unclassified spikes, mainly artifacts and occasional distorted action potentials, were removed. This concerned well <1% of all spikes.

Figure 2.

Spike sorting. A, A short segment of an extracellular recording from an A:B1 nerve (black) with spikes from multiple sources indicated (colored symbols). The spikes marked with red crosses represent the action potentials in the P cell (intracellular trace shown in gray). Calibration: 200 ms, 100 μV (100 mV for intracellular trace). B, Montage of all the spike waveforms in the various clusters extracted from this recording. Colors correspond to the colors in A. Calibration: 2 ms, 100 μV. C, Consistency test of spike sorting results. Spike waveforms of identified clusters on A:B1 (left) and corresponding spike-triggered averages of simultaneously recorded ipsilateral PP:B1 nerve (right). Scale as in B.

Quantifying stimulus responses.

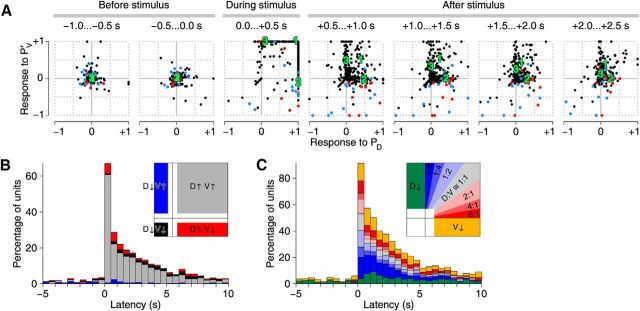
Responses in each of the units (putative motor neurons) from which we recorded in a given experiment were combined into a high-dimensional vector in which each dimension represented the number of spikes fired by a particular (putative) neuron. We subtracted the baseline firing rate, calculated over long stretches of recording between stimuli. (The alternative, calculating baseline over just the last several seconds before a particular stimulus yielded estimates that were too noisy for practical use due to relatively low firing rates; the scatter in the two “before stimulus” panels in Fig. 5A reflect this stochastic firing.)

Figure 5.

Time evolution of responses to P_D and P_V^c stimulation. A, Responses (i.e., baseline-subtracted firing rates) of 367 isolated putative neurons (dots) in 35 ganglia to stimulation of a P_D neuron (x-axis) or the contralateral P_V neuron (P_V^c) (y-axis). Panels represent consecutive 0.5-s-wide windows. Units positively identified as DE-3 neurons ipsilateral to the P_D neuron are colored red (n = 11); contralateral blue (n = 14). B, Units that responded to both P_D and P_V^c stimulation classified by the signs of their responses as a function of time. Red represents units with firing rate upregulated by P_D stimulation and downregulated by P_V^c stimulation. Black represents units downregulated by both. Gray represents units upregulated by both. Blue represents units downregulated by P_D stimulation and upregulated by P_V^c stimulation. (Numbers do not add up to 100% because only units that, in a given time window, had firing rates >0.5 SD different from their baseline in both P_D and P_V^c conditions are included in this graph.) Inset, How the various regions in the panels in A are represented in B. White indicates regions not represented. C, Units that responded to either P_D or P_V^c stimulation with a firing rate increase classified by the ratio of those increases (“D:V”). (Numbers do not add up to 100% because only units are included that, in a given time window, had firing rates >1 SD above their baseline in at least one of the two stimulus conditions.) Inset, How the various regions in the panels in A are represented in C. White indicates regions not represented.

If we had K trials in which, for example, the P_D cell received n pulses, we wrote f⃗_k,n^D for the response in the k-th such trial. We then defined the “canonical dorsal response” in this ganglion as follows:

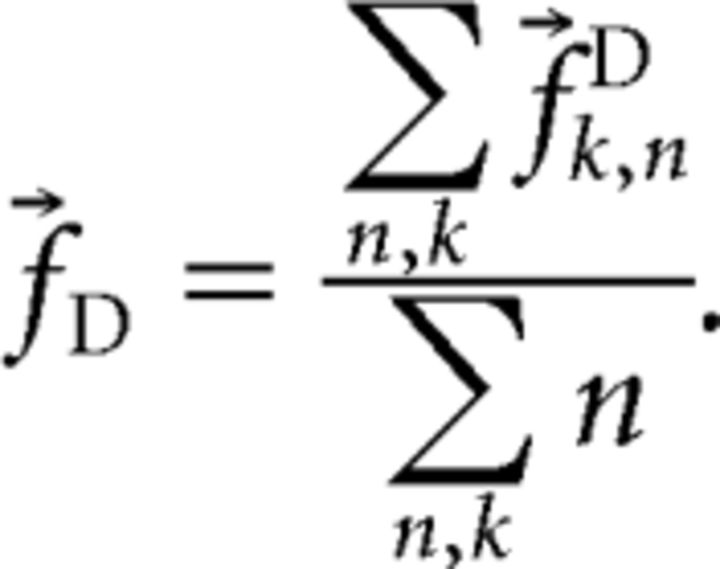Each component in f⃗_D thus represents the number of spikes recorded on average per P_D-cell stimulus in a given motor neuron.

We then used this canonical response to model the responses in trials in which (only) P_D cells were stimulated as follows:

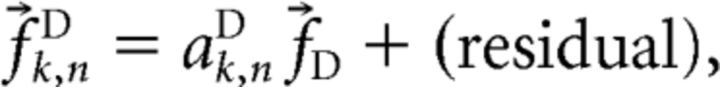and determined the values for the scaling coefficient a_D in each of the trials. The procedure is illustrated in Figure 3.

Figure 3.

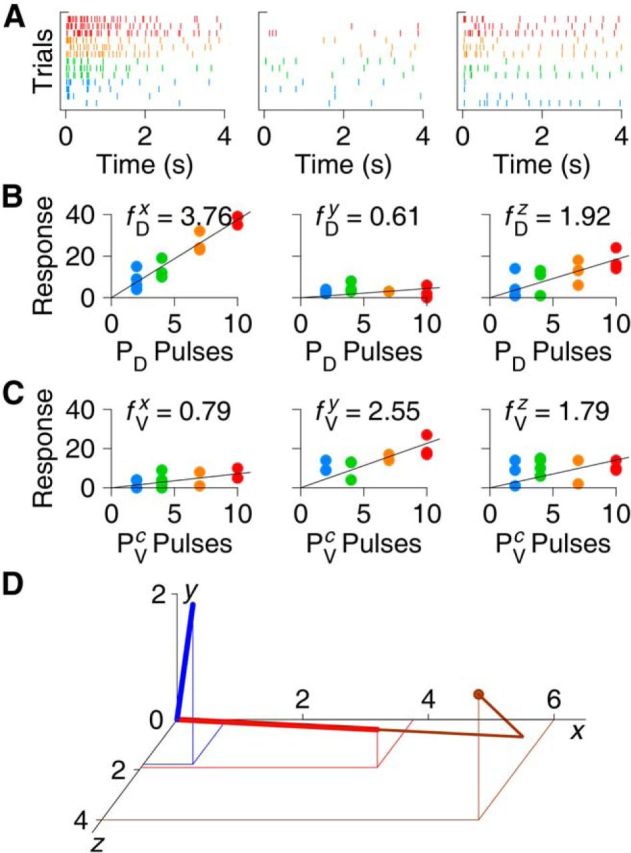
Illustration of the calculation of canonical responses. A, Raster plot of responses to P_D stimulation with 2, 4, 7, and 10 pulses (blue, green, orange, and red, respectively) in three arbitrarily chosen cells simultaneously recorded in one ganglion. B, Response count (number of spikes detected in first 4 s) as a function of number of pulses in the stimulus; same three cells as in A. Arbitrarily calling these cells “x,” “y,” and “z,” we calculate the x-, y-, and z-components of the canonical dorsal response vector f⃗_D based on these graphs. C, Response count for stimulation to the contralateral P_V cell. The x-, y-, and z-components of the canonical ventral response vector f⃗_V are based on these graphs. D, Visualization of the canonical dorsal (red) and ventral (blue) responses in three dimensions with projection down to the x,z plane. Also shown is the decomposition of a response in a single trial to a train of two pulses to P_D as a scalar multiple of f⃗_D plus a residual (brown). This illustration is based on a small subset of the data from one experiment; the full dataset obtained from one experiment comprises recordings from ∼10–20 neurons, which would yield rather high dimensional graphs.

We then proceeded to model the scaling coefficient itself as a function of the number of stimulus pulses n as follows:

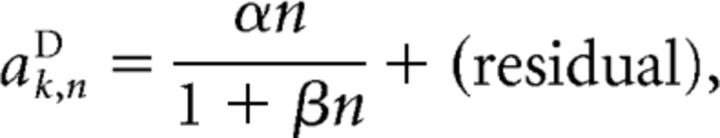where α and β were determined using linear least-squares fitting.

A “canonical ventral response,” f⃗_V, was analogously constructed and used to model trials in which only P_V cells were stimulated.

These same canonical response vectors were also used to model trials in which a P_D cell received n stimulus pulses while the P_V^c cell simultaneously received m pulses. The only difference was that we now modeled the response as follows:

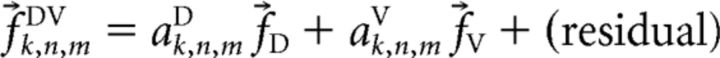and the scaling coefficients as follows:

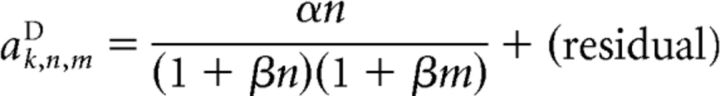and

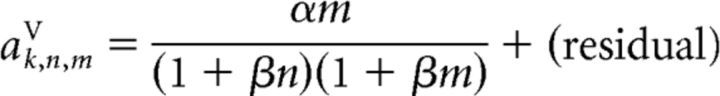respectively. It is important to note that, despite the more complex stimulus conditions in these trials, the scaling of the responses was still modeled with only two free parameters, α and β.

Quantifying “dorsality” of responses.

To quantify to what degree responses in a certain experimental condition are more “like” responses to pure dorsal or pure ventral stimulation, we introduced a “dorsality” index by adapting Fisher's linear discriminant analysis (LDA; Fisher, 1936).

We started from the average number of spikes f_c^D(t) in cell c, latency bin t, following pure P_D stimulation in a given ganglion (the “P_D response”), the trial-to-trial covariance of this response, Σ_c,c′^D(t), and the analogous quantities for pure P_V^c stimulation. Fisher's LDA introduces a separability:

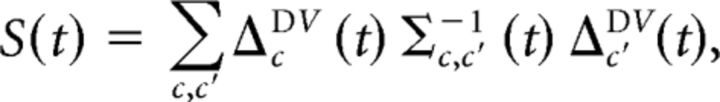in which Δ_c^DV(t) ≡ f_c^D(t) − f_c^V(t) and Σ(t) = Σ^D(t) + Σ^V(t). This separability quantifies how well responses to P_D stimuli can be distinguished from responses to P_V^c stimuli. In Fisher's LDA, responses can then be classified as either belonging to the P_D class or the P_V^c class depending on whether the discriminant

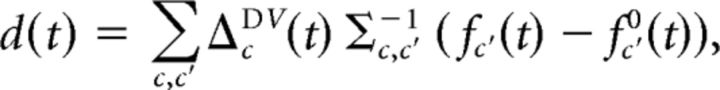where f_c⁰(t) = $\frac{1}{2}$(f_c^D(t) + f_c^V(t)), is positive or negative for a trial with recorded firing rates f_c′(t).

Although powerful and useful in many situations (e.g., Briggman et al., 2005), this formalism has two shortcomings for our application. The first is a purely computational one: Calculating the full covariance matrices is numerically unstable when the number of cells is large. We overcome this by approximating the full matrix by a diagonal matrix with estimated per-cell variances based on assuming approximately Poissonian firing: (σ_c^D(t))² = f_c^D(t)/K, where K is the number of trials. (And analogously for P_V^c stimulation.) This simplifies the separability to the following:

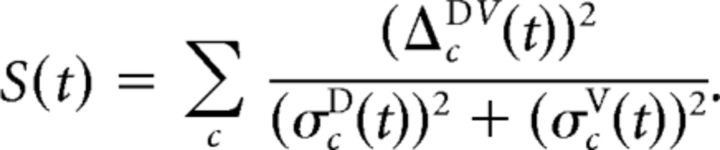A second, more fundamental, shortcoming is that S(t) is not bounded and depends strongly on the number of cells recorded. Although it makes sense that response classes are more separable when we have more detailed information about those responses, a measure of the actual difference between the classes should not depend on such experimental details. We therefore introduced the following measure of separation between dorsal and ventral responses:

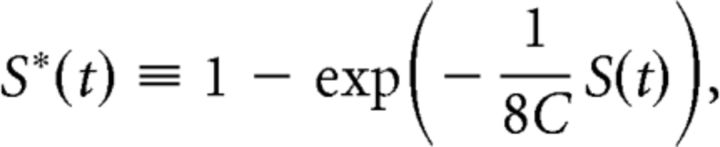where C is the number of cells recorded from in a given experiment. This separation ranges from 0 to 1: S* = 0 meaning that P_D and P_V^c responses are indistinguishable; S* = 1, meaning that some cell fired infinitely fast following P_D stimulation and not at all following ventral stimulation, or vice versa. And under reasonable assumptions of statistical properties, S* does not depend on the number of cells recorded in a particular experiment. In practice, S* values between 0.5 and 0.7 were commonly observed shortly after stimulation (see Fig. 7).

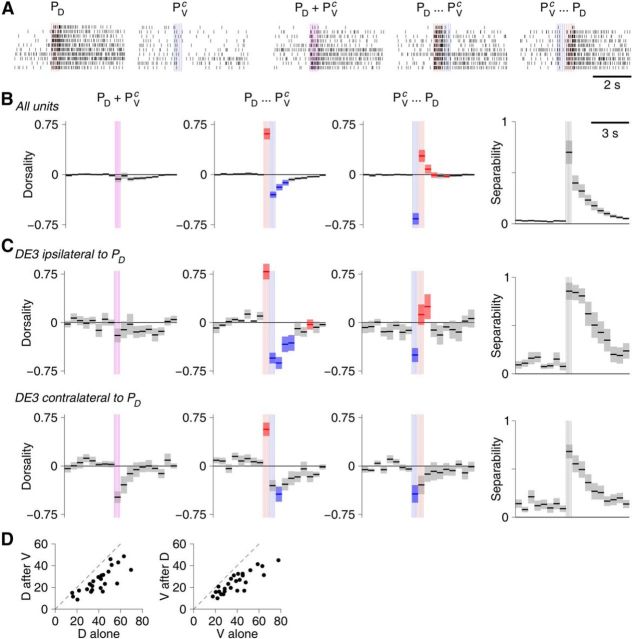
Figure 7.

Stimulus responses can be overridden by secondary stimulation. A, Example raster plots of DE-3 cell responses to stimulation of either: only the ipsilateral P_D neuron; only the contralateral P_V neuron; both simultaneously; P_D followed by P_V^c; P_V^c followed by P_D. B, “Dorsality” (see Materials and Methods) of vector responses to simultaneous or sequential stimulation as a function of time. Lines and area represent mean ± SE. Red areas indicate significantly higher dorsality than in simultaneous case. Blue areas indicate significantly lower dorsality than in simultaneous case. Vertical colored lines indicate timing of stimuli. Rightmost column represents separation (see Materials and Methods). C, Dorsality of responses in specific cell types: DE3 cell ipsilateral (top) and contralateral (bottom) to the stimulated P_D neuron. D, Number of spikes contributed in the first 0.5 s by P_D stimulation with or without preceding P_V^c stimulation (left) and vice versa (right) in N = 26 experiments.

Given observed average number of spikes f_c^X(t) in cell c, time bin t, in trials of stimulus condition X, we then calculated the dorsality index for condition X as follows:

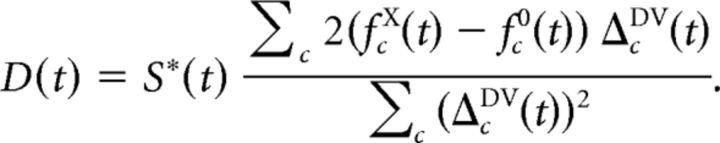Assuming perfect separation between P_D and P_V^c responses, this index would approach 1 if the responses in condition X were identical to responses to pure P_D stimulation and −1 if the responses in condition X were identical to responses to pure P_V^c stimulation. If the responses in condition X were equally similar to those following pure P_D and pure P_V^c stimulation, or in time bins where separation is low, the dorsality index approaches 0.

As introduced above, D(t) is defined as a single number for the whole population of motor neurons recorded in a given experiment, but it can equally be defined for an individual neuron: simply by not summing over cells.

Results

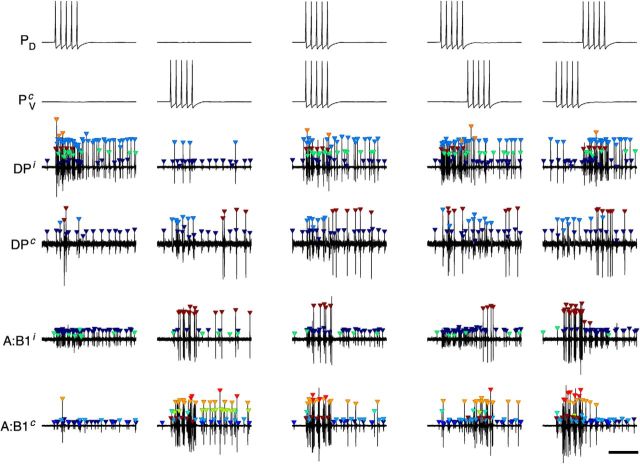
Stimulating a P cell intracellularly with trains of 5 pulses at 10 Hz reliably evoked precisely 5 action potentials in that cell. Stimulating P cells in this manner resulted in responses in many motor neurons (Fig. 4). This was true when only one P cell was stimulated at a time (left two columns), and also when two diametrically opposed P cells were stimulated simultaneously (middle column) or sequentially (right two columns). In all cases, the response outlasted the stimulus itself by several seconds. Responses lasting up to 10 s were common (data not shown here, but see Fig. 5).

Figure 4.

Motor neuron responses to P-cell stimulation. Left to right, Columns show single examples of responses to stimulating a P_D neuron, the contralateral P_V neuron (P_V^c), both simultaneously, or one followed by the other. Top to bottom, Rows show intracellular traces in the P_D and P_V^c neurons followed by extracellular traces from four different nerves, all recorded simultaneously (see Fig. 1). Superscript “i”: ipsilateral to P_D; superscript “c”: contralateral to P_D. Plot symbols represent spikes and their cluster assignments. Calibration: 500 ms.

Although Figure 4 suggests that responses differ significantly depending on which P cell(s) was/were stimulated (and raster plots, not shown, confirm this), an analysis of the responses of all recorded units recorded from 35 experiments actually revealed that the vast majority of motor neurons responded to both P_D and P_V^c stimulation by increasing their firing rates (Fig. 5A). Notable exceptions were the dorsal exciter neurons DE-3. DE-3 neurons ipsilateral to the stimulated P_D cell (Fig. 5A, red dots, mostly in lower right quadrant) exhibited a strong increase in firing rate following P_D stimulation, whereas following P_V^c stimulation (i.e., stimulation to a P_V cell contralateral to the DE-3 neuron), they either decreased their firing rates slightly or were unaffected. DE-3 neurons contralateral to the stimulated P_D cell (Fig. 5A, blue dots) exhibited mixed responses following P_D stimulation, whereas following P_V^c stimulation (i.e., stimulation to a P_V cell ipsilateral to the DE-3 neuron), they mostly decreased their firing rates slightly.

The leech is justly famous for the high degree of stereotypy of its ganglia, so one might reasonably hope that recorded units could be identified with specific known neurons, based, for instance, on their spike waveforms and projection patterns through the various nerves (Ort et al., 1974). Indeed, positively identifying the DE-3 neurons was straightforward using these criteria. Naturally, we attempted to cluster the other units (both manually and semiautomatically) so as to obtain a mapping between units and known neurons. To our surprise, however, we found that the variability between ganglia was such that we were unable to do so with the desired degree of confidence. Ultimately, we had to accept that it was safest to perform the rest of the analysis based on “units,” without making specific claim to neuronal identities.

Of those units, then, that responded to both P_D and P_V^c stimuli with a significant change in firing rate, the vast majority responded positively to both (gray bars in Fig. 5B), whereas only a small minority responded in opposite directions (red and blue bars). That is not to say that most cells do not distinguish between P_D and P_V^c stimulation: if we consider all units that responded with an increase in firing rates to at least one kind of stimulus, most exhibited a strong preference either for P_D stimulation (Fig. 5C, red and yellow bars) or for P_V^c stimulation (blue and green bars), whereas only a small fraction responded approximately equally strongly to the two (gray and pale colored bars).

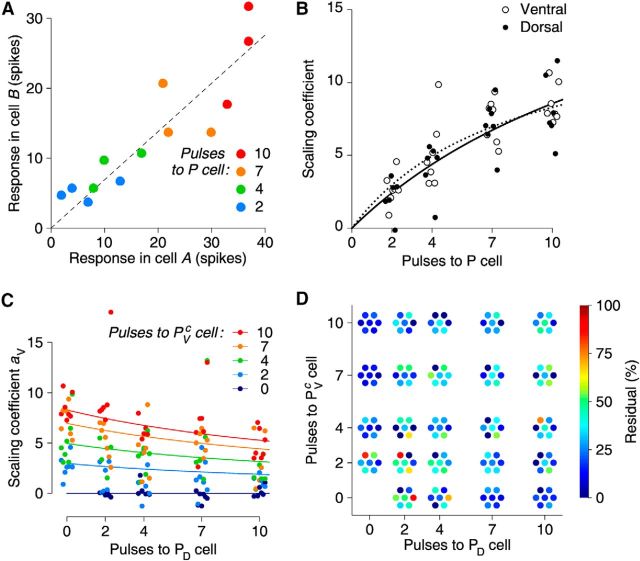
Thus far, we have discussed motor neuron output qualitatively. Is a concise quantitative description as a function of the stimulus input also possible? Using stimuli of 2–10 pulses delivered in a 500 ms train, we first asked whether the activity of an arbitrarily selected pair of motor neurons scaled proportionally as stimulus strength (number of pulses delivered to the P cells) was increased. We found that this was the case (Fig. 6A). In other words, the relative strength of the responses of motor neurons was unaffected by stimulus strength, as long as the stimulus site (which P cell was stimulated) remained the same. As a consequence, we could express responses to different strengths of stimulation at a given site as scalar multiples of a “canonical response vector” for that stimulus site (Fig. 6B; see Materials and Methods). We found that the response magnitude (vector length of firing rate vector) as a function of stimulus strength (again, number of stimulus pulses) obeyed a simple, gently sublinear scaling law: ||f|| ∼ n/(1 + βn), where f is the response vector, n is the number of stimulus pulses, and β = 0.06 ± 0.04 for dorsal and β = 0.12 ± 0.07 for ventral stimulation. These numbers were not significantly different from each other. What is more, this scaling law could also be used to predict responses to mixed stimuli (where both P_D and P_V^c received a number of stimulus pulses; Fig. 6C), again with fit parameters α and β that were not significantly different. This simple paradigm explained the great majority of the variance in the responses (Fig. 6D).

Figure 6.

Motor neuron responses scale predictably as a function of stimulus strength. A, Responses of two arbitrarily selected cells (“A” and “B”) from a typical experiment scale nearly equally with increasing stimulus strength (color coded). Dotted line indicates equal scaling. B, Scaling coefficient of vector responses as a function of stimulus strength, for responses to simple P_D stimulation (disks and solid best-fit line) and for simple P_V stimulation (circles and dotted best-fit line). Each marker (at a given stimulus strength) represents data from one preparation; n = 7 preparations with 15 ± 6 isolated units each. Markers were displaced by a slight amount in the horizontal direction for increased visual clarity. C, Ventral scaling coefficient of vector responses to combined P_D and P_V^c stimuli as a function of strength of stimulation to the P_D neuron (x-axis) and the P_V^c neuron (colors) with best-fit traces. As in B, each marker (at a given stimulus strength) represents an individual preparation, and markers were displaced horizontally for clarity. D, Residuals of response vector length after model fitting. Markers displaced for clarity.

These results so far indicated that the local bend responses to multiple stimuli could be described as a simple linear combination of the responses to individual stimuli (with slightly sublinear scaling coefficients). Is this really true in all stimulus conditions? To test this, we delivered trains of 5 pulses (at 10 Hz) either simultaneously to P_D and P_V^c or with a 500 ms delay. We compared responses to temporally displaced stimuli (P_D before P_V^c or vice versa, as in the last two columns of Fig. 4) with responses to simultaneous stimuli. Raster plots obtained from an example neuron (Fig. 7A) suggest that the system does indeed differentiate between these cases. To further investigate, we introduced a “dorsality index” (see Materials and Methods), which indicates to what extent the response at a certain latency after an arbitrary stimulus is “like” the response at the same latency following a pure P_D stimulus or whether it is more like the response to a pure P_V stimulus. This metric could be applied either to the complete (vector) response of all units in a recording (Fig. 7B) or to individual units (Fig. 7C).

We found that in either case, responses to simultaneous stimuli had near-zero dorsality, indicating that these responses were approximately equally similar (or dissimilar) to pure P_D responses and pure P_V^c responses (Fig. 7B,C, left column). The fact that the dorsality was more often slightly negative than slightly positive may be due to sampling bias: our recordings contained more signals from neurons that innervated ventral muscles than dorsal muscles.

Strikingly different results were obtained from nonsimultaneous stimuli. When the P_D cell was stimulated first (second column), the initial response (before the P_V^c received its stimulus) had very high dorsality. So far, no surprise: up to that point the stimulus essentially was a pure P_D stimulus. But following the second stimulus, the responses had significantly more negative dorsality than observed after simultaneous stimulation. Conversely, when the P_V^c stimulus preceded the P_D stimulus, dorsality was initially very negative (again, unsurprising), but after the P_D stimulus arrived became significantly more positive than observed following simultaneous stimulation. This could not be attributed to sensitization, in which the first stimulus primes the system to respond more strongly to a second stimulus (Lockery and Kristan, 1991): A ventral stimulus following a dorsal stimulus contributed only 0.62 ± 0.02 times as much to the total firing rate as a ventral stimulus did in isolation, and a dorsal stimulus following a ventral stimulus contributed 0.65 ± 0.03 as much as a dorsal stimulus in isolation: all the data points in Figure 7D lie below the y = x line. Instead, these results indicate that for sequential stimulation, the second stimulus to some degree “overrides” the first stimulus.

Discussion

It has long been known that one class of sensory neurons, the P cells, is largely responsible for triggering the medicinal leech's local bend response (Kristan, 1982). Since then, the local bend reponse has been studied using many modalities, including videorecorded responses, electromyography, and voltage-sensitive dye recordings (e.g., Lewis and Kristan, 1998b; Baca et al., 2005, 2008). The circuitry underlying the response has been probed in detail by stimulating P cells either individually or in neighboring pairs (Lockery and Kristan, 1990a, b), but at the level of individual motor neurons, the response to stimuli that activate diagonally opposed P cells was considered too variable for analysis (Lockery and Kristan, 1990a).

By recording simultaneously from large numbers of motor neurons in a single ganglion using up to four nerve suction electrodes, we were, for the first time, able to analyze in detail the local bend response to stimuli that activate diametrically opposite P cells. In contrast to adjacent P cells, diametrically opposite P cells can never be coactivated by a single localized physical stimulus because their receptive fields are well separated (Fig. 1A) (Nicholls and Baylor, 1968). Accordingly, although it makes sense for a leech to interpret coactivation of adjacent P cells as a single physical stimulus to a location between these cells' receptive fields, coactivation of opposite P cells allows no such interpretation. Instead, one possible interpretation might be as a pinch, such as a leech might experience when a predator tries to grab it, which might warrant an escape response quite distinct from a local bend.

So one could, a priori, expect any number of responses to bilateral stimuli: The response could be a linear combination of the responses to individual stimuli. This happens in perhaps the most simple form in the McGurk effect in humans, in which logically unconnected visual and auditory cues nevertheless are experienced as connected (cited in Stein, 1998). The human brain performs a more sophisticated form of linear combination in visuo-vestibular conflict processing (a putative underlying cause of motion sickness) (Warwick-Evans et al., 1998), which was successfully modeled as a process of Bayesian integration (Butler et al., 2010).

Alternatively, one or the other stimulus might dominate the response, possibly as a function of relative stimulus strength or salience. Such an outcome could be considered in the context of behavioral choice (e.g., Shaw and Kristan, 1997; Briggman et al., 2005; Körding and Wolpert, 2006).

Lastly, the response could be completely different from the responses to individual stimuli. This might, for instance, make sense when responding to the detection of two predators approaching from opposite directions so that fleeing directly away from either one would not be adaptive. This outcome could also be considered in the context of behavioral choice.

Existing work on the local bend response in the leech has pointed at a continuous rather than a categorical encoding of stimulus location (Lewis and Kristan, 1998c), which would predict the first of these three outcomes. However, those results were obtained using a congruent set of stimuli. When diametrically opposed stimuli were applied, outcomes were “variable between preparations, resembling most single PD stimulation” (Lewis and Kristan, 1998c), which might predict the second of the three outcomes. When considering the sequential stimulation (Figs. 4 and 7), the literature provides less guidance to our expectations because previous work (Thomson and Kristan, 2006) focused on the timing of responses rather than the timing of stimuli. However, in certain other cases where multiple behaviors compete for expression, a hierarchy has been observed such that certain behaviors always override certain others (Gaudry and Kristan, 2010). In yet other cases, perhaps when the competing behaviors were more at par, it was found that, as the first stimulus had more time to bring the system to its corresponding state, a second stimulus had an increasingly hard time driving the system, suggesting the presence of attractor dynamics (Briggman et al., 2005).

The reality we observed for simultaneous stimuli was the simplest possibility: we found that the propensity of the local bend system to integrate simultaneous stimuli across neighboring receptive fields also extends to opposing receptive fields, fitting well the model proposed by Lewis and Kristan (1998a): the system treats such apparently conflicting stimuli just like it does nonconflict stimuli and responses to simultaneous stimuli could be modeled with a simple linear model that used identical parameter values used to model the nonconflict situation, and no additional parameters. The fact that a single scaling parameter describes the complex responses is very well in line with central inhibition governing the gain of the circuit (Baca et al., 2008). In a future study, it would be of great interest to compare individual neurons between preparations and quantify the variability reported earlier.

In contrast to what we found for simultaneous stimuli, responses to sequential pairs of stimuli could not be predicted by a simple linear combination of the isolated responses to the constituent stimuli. In this situation, the second stimulus of the pair had the greatest influence on the ultimate response, in contrast to what one might expect from a simple reflex pathway in which an initial stimulus sets in motion a response sequence that is impervious to subsequent stimuli (possibly through a mechanism akin to the attractor dynamics proposed by Briggman et al., 2005). This is especially notable because the local bend response lasts considerably longer than the stimulus that triggers it, implying that the underlying circuit must feature some form of positive feedback loop to sustain it. (Our present results do not allow us to determine whether this feedback is implemented as a synaptic loop or as a cellular mechanism in the local bend interneurons.) The fact that the second of a pair of consecutive stimuli had greater influence on the ultimate response implies that this positive feedback is not strong enough to lock the system in a particular response independent of subsequent input. From an ethological perspective, this makes sense because it is surely adaptive for an animal to update its behavioral output when conditions change.

Sensory conflicts have been a classic subject in philosophy since long before neuroscience emerged as a separate discipline: a version of the familiar paradox of the donkey stuck midway between a stack of hay and a pail of water because it is equally driven by hunger and thirst dates back to Aristotle (cited in Rescher, 2005). The connected issue of how the brain determines whether or not two simultaneous sensory events relate to the same physical object, the so-called binding problem, has also been studied extensively by neuroscientists and psycholigists alike (e.g., Treisman, 1998).

The leech may not be an ideal animal to study the binding problem in its full glory, simply because its perceptual state space is probably too small. Regardless, our extensive characterization of the local bend response to conflicting, or at least largely incongruent stimuli, opens up a new avenue of research into how nervous system process sensory conflicts. It provides a new model to study, for instance, the role of interneuronal network dynamics, in a context where inputs can be precisely controlled and outputs exhaustively measured. Meanwhile, it builds on the extensive knowledge and anatomical detail we already have from the study of the local bend circuit in the context of other questions. Finally, with increasingly high dimensional recordings ever more common throughout neuroscience, the analytical methods presented in this paper may find broader application in describing and understanding complex sensory processing in terms of the constituent stimuli.