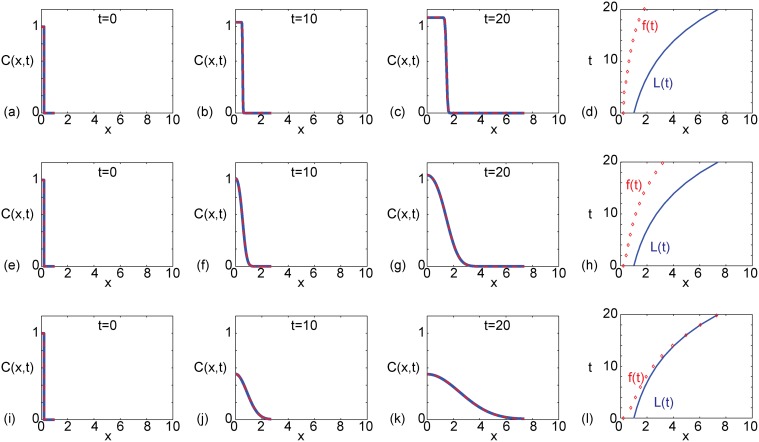
Fig 1. Comparison of exact and numerical solutions, exploring the influence of varying the diffusivity, D.

All results correspond to an exponentially-elongating domain, L(t) = L(0)exp(αt), with L(0) = 1 and α = 0.1. The initial condition is given by Equation (5) with β = 0.2 and C ₀ = 1. In all cases we consider a linear source term with k = 0.105. Results in (a)–(d) correspond to D = 1 × 10⁻⁵, results in (e)–(h) correspond to D = 1 × 10⁻³, and results in (i)–(l) correspond to D = 1 × 10⁻². For all three sets of parameter combinations we show the solution at t = 0,10 and t = 20, as indicated. The exact solutions, presented in (a)–(c), (e)–(g) and (i)–(k) (solid blue), correspond to Equation (13), where we truncate the infinite sum after 1000 terms. The numerical solutions, presented in (a)–(c), (e)–(g) and (i)–(k) (dashed red), are numerical approximations of Equation (7) with δξ = 0.001 and δt = 0.001. The space–time diagrams summarising the time evolution of the length of the domain, L(t), and the position of the front of the C(x, t) density profile, f(t), given in (d), (h) and (l), are constructed by defining f(t) to be the position where C(x, t) = 0.01.