Abstract
Magneto-chiral dichroism (MχD) is a non-reciprocal, i. e. directional, effect observed in magnetised chiral systems featuring an unbalanced absorption of unpolarised light depending on the direction of the magnetisation. Despite the fundamental interest in a phenomenon breaking both parity and time reversal symmetries, MχD is one of the least investigated aspects of light-matter interaction because of the weakness of the effect in most reported experiments. Here we have exploited the element selectivity of hard X-ray radiation to investigate the magneto-chiral properties of enentiopure crsytals of two isostructural molecular helicoidal chains comprising Cobalt(II) and Manganese (II) ions, respectively. A strong magneto-chiral dichroism, with Kuhn asymmetry of the order of a few percent, has been observed in the Cobalt chain system, while it is practically absent for the Manganese derivative. The spectral features of the XMχD signal differ significantly from the natural and magnetic dichroic contributions and have been here rationalized using the simple multipolar expansion of matter-radiation interaction.
The interest in the interplay between chirality and magnetism dates back to Pasteur,1 but intense research is still devoted to it,2 being relevant for a wide class of phenomena that range from exotic magnetic excitations known as skyrmions3-5 to magnetochiral conductance.6 The interaction between light and matter is a powerful tool to investigate the simultaneous breaking of spatial symmetry, i.e. the lack of inversion symmetry, and of the time reversal symmetry, as in the case of a magnetized non-centrosymmetric medium. Magnetism and chirality are indeed directly connected through the magneto-chiral dichroism and birefringence,7-10 which was observed for the first time by Rikken & Raupach11 in luminescence spectra and successively using X-ray radiation.12 Magneto-chiral dichroism, (MχD) is a non-reciprocal effect consisting in different absorption of unpolarized light by a chiral magnetized medium. It is a fascinating parity violating phenomenon that has been suggested to be at the origin of homochirality of life on earth13-15 as an alternative to electroweak nuclear interactions.16 MχD is generally a very weak effect, with only few examples reported17-21 and a limited knowledge available on the factors that originate the phenomenon.
The conditions of simultaneous breaking of parity and time-reversal symmetry required to observe the phenomenon are satisfied in magneto-electric media and multiferroics,22,23 but they can also be fulfilled in molecular paramagnetic and diamagnetic systems in the presence of an external magnetic field. The systems investigated here, consisting of isostructural molecular helicoidal chains comprising either anisotropic Cobalt(II) or isotropic Manganese(II) ions, can be considered intermediate between these two classes. A thorough investigation of the magnetochiral effect through X-ray spectroscopy at the K-edge of the 3d-metals, evidencing a strong magnetochiral dichroism in the cobalt chain system, is here described.
We investigated two isostructural one-dimensional (1D) molecular chains of formula [M(hfac)2NITPhOMe]∞ comprising bipositive metal ions (M=MnII and CoII) shielded by ancillary ligands (hfac-=hexafluoroacetylacetonato) and bridged by stable nitronyl-nitroxide organic radicals (NITPhOMe = 2-(4-meth-oxyphenyl)-4,4,5,5-tetramethylimidazoline-l-oxy1,3-oxide) carrying a delocalized unpaired electron.24,25 The helical structure of [M(hfac)2NITPhOMe]∞, [M-NIT]∞ hereafter, is generated in the crystalline phase by a three-fold screw axis (see Figure 1). Despite the absence of chiral constituents the compounds form enantiopure crystals, crystallising either in the chiral P31 or P32 space groups.24,25 The compounds are optically active and exhibit a significant second harmonic generation efficiency.26 The magnetism of both compounds is governed by the strong intra-chain antiferromagnetic exchange interaction between the alternating paramagnetic metal ions and the spin S=1/2 of the organic radicals, with exchange constant, J =235K and 495 K for the Co27 and Mn24 derivative, respectively. The exchange Hamiltonian for a chain of N spins is defined as , where the small s on odd sites represents the radical spin while the capital S on s even sites either the CoII or MnII spin. A completely different behaviour is however observed depending on the metal ion. In the case of MnII, Heisenberg 1D ferrimagnetic behaviour is observed due to the lack of orbital contribution for this d5 ion, with strong long range correlations and 3D ordering around T= 5 K induced by the weak interchain dipolar interactions.24 On the contrary, high spin CoII ions in octahedral environment have a significant orbital moment resulting in a strong magnetic anisotropy with the easy axis of magnetization of each ion forming an angle of ca. 50° from the helix axis (Figure 1a). Interestingly the Cobalt derivative was the first system exhibiting slowing down of the magnetization dynamics in the paramagnetic phase, as predicted by Glauber for the 1D Ising model.28 An activation barrier of about 170 K for the reversal of the magnetization characterizes this material, and magnetic hysteresis in the absence of long range order is observed below 5 K.25 Finite size effects with collective reversal of spin segments29 and an unprecedented mechanism to control magnetization dynamics through light-induced domain-wall kickoff has also been recently observed in this fascinating material.27
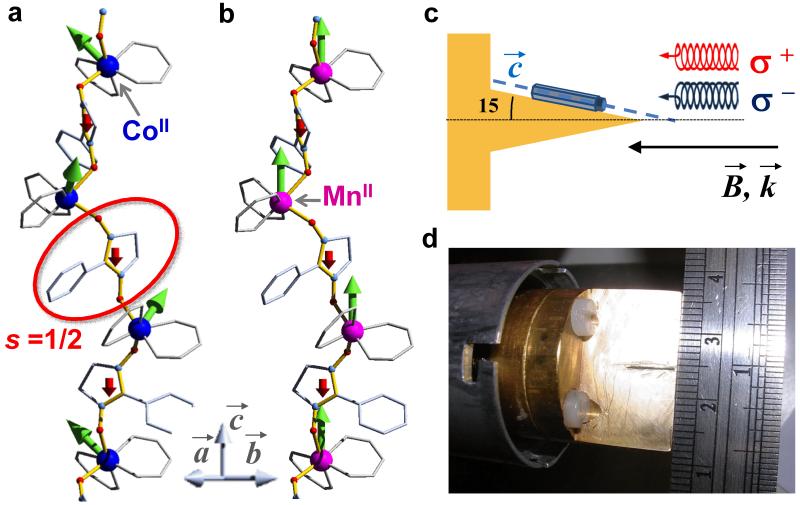
Figure 1. Structures of the molecular magnetic helices and experimental set-up.
View of the simplified structure of the [M-NIT]∞ molecular helices containing CoII (a) and MnII(b) ions bridged by organic nitronyl-nitroxide radicals, with a radical unit highlighted by the red circle. The metal ions are highlighted as large spheres. The ancillary hfac ligands and the radical backbone are in grey, while the conjugated bonds carrying the magnetic exchange interaction are highlighted in yellow, with the radical oxygen atoms in red and nitrogen ones in blue. Some group of atoms, i.e. CF3, CH3, and O-CH3, have been omitted for the sake of clarity. The helices develop along the crystallographic c axis of the P31/P32 space groups. The green arrows represent the orientation of the magnetic moments when the magnetic field is applied parallel to the c axis, which are not collinear to the field in the case of the anisotropic CoII ions. c) Schematic side view of the geometry of the experiment where needle-like single crystals were mounted on a copper sample holder to form an angle of 15° between the chain direction and the propagation vector, , of the X-rays, which is parallel to the applied magnetic field. d) Photography of the sample mounting viewed from the top, with a ruler for reference.
To investigate the magnetochiral dichroism of these 1D molecular crystals hard X-ray radiation was used to get element-specific information. The excellent stability of the ID12 beamline of ESRF resulted to be mandatory to investigate single crystals of [Mn-NIT]∞ and [Co-NIT]∞ chains with small dimensions (0.3×0.3×8 mm). X-ray absorption near edge spectra (XANES) were measured at the Co and Mn K-edges, i.e transitions promoting electrons from the 1s core level occurring around 7.7 keV and 6.5 keV, respectively, using total X-ray fluorescence yield detection mode (see methods for details).
By recording the XANES spectra with opposite σ+ (circular left) and σ-(circular right) polarizations and with a magnetic field applied either parallel or antiparallel to the X-ray wavevector, B±, we could obtain the three relevant dichroisms:
| (1) |
| (2) |
| (3) |
where μ(σ,B) stands for the absorption measured for the indicated polarization and sign of the magnetic field. XN(M)CD indicate X-ray natural (magnetic) circular dichroism signals and are defined as the difference in absorption spectra recorded with the two circular polarizations. The XNCD signal is independent of the applied magnetic field, whereas XMCD changes its sign when the direction of applied magnetic field is reversed. The magneto-chiral effect manifests as changes in absorption for two directions of magnetic field and as such does not require polarized light. In order to be able to disentangle the XMχD from other dichroic contributions we sum up the spectra recorded with right and left circularly polarized X-rays. The spectra accumulation was performed changing field polarity and light helicity in a cyclic way to minimize eventual drift effects in the evaluation of the dichroic quantities. No detectable radiation damage was observed for all investigated crystals.
First, room temperature XNCD spectra were recorded on several crystals to identify two enantiomeric crystals of each [M-NIT]∞ chain; then the selected crystals were transferred to an experimental station equipped with a 17 Tesla superconducting magnet and constant flow Helium cryostat. These crystals were mounted on the cold finger of the cryostat and oriented with the crystallographic c (helix) axis forming an angle of 15° with the vector of propagation of the light , the latter being parallel to the applied magnetic field , (Figure 1c-d). A field of 3 T was employed at T=5 K to ensure the magnetic saturation for crystals of both Mn and Co chains and to suppress the slow magnetic relaxation for the latter.
Before describing the results we briefly recall here some fundamental differences in the interaction between matter and light when moving from UV-visible to hard X-ray radiation. Being atomic core states involved in X-ray promoted transitions, the long wavelength approximation is still valid despite the high energy. Thus the interaction can be expressed in the usual multipolar expansion:
| (4) |
where E1 stands for the interaction between the electric dipole and the electric field of the electromagnetic radiation, M1 for the magnetic dipole – magnetic field interaction, and E2 for the electric quadrupole – electric field gradient interaction. Differently from UV-Vis, in X-ray spectroscopy M1 interaction is negligibly small, involving atomic states with different principal quantum number, while E2 becomes relevant, given its linear dependence with the energy of the transitions.
As the absorption cross section is proportional to the square of the transition matrix pure electric dipolar (E1E1), magnetic dipolar (M1M1) and electric quadrupolar (E2E2) contributions and two interference terms (E1M1) and (E1E2) must be considered. The latter is a traceless rank-2 tensor and, in contrast to the pseudoscalar E1M1 term, it averages to zero in randomly oriented samples. In X-ray spectroscopy it is thus necessary to work with a single crystal or to break artificially the orientational isotropy of space, for example by dissolving a chiral molecule in an aligned liquid crystal.30
This drawback, compared to visible-UV experiments, is fully compensated by the fact that high optical quality and transparency of the crystals is not required. Moreover birefringence is very small, particularly at the high energies employed here. The greatest advantage of X-ray spectroscopy is its element selectivity, which allows to selectively address the magnetic centres.
The different dichroic contributions to X-ray absorption and their symmetry properties are summarized in Table 1. Note that time reversal symmetry can be broken either by the spontaneous magnetic ordering in the sample or by the application of an external magnetic field.
Table 1. Different dichroic contributions to the radiation-matter interaction.
The involved mixed terms of the radiation-matter interaction and their parity behaviour is listed for each type of dichroism. M stands for the sample magnetization. For the sake of completeness we recall that other dichroisms can be obtained with linearly polarized light. These are: X-ray linear dichroism, X-ray magnetic linear dichroism, which are both parity and time-reversal even, and non-reciprocal linear dichroism, which is parity odd and time-reversal odd.
| Parity | Time Reversal | ||
|---|---|---|---|
| XNCD | E1M1+E1E2 | − | + |
| XMCD | + | − | |
| XMχD | − | − |
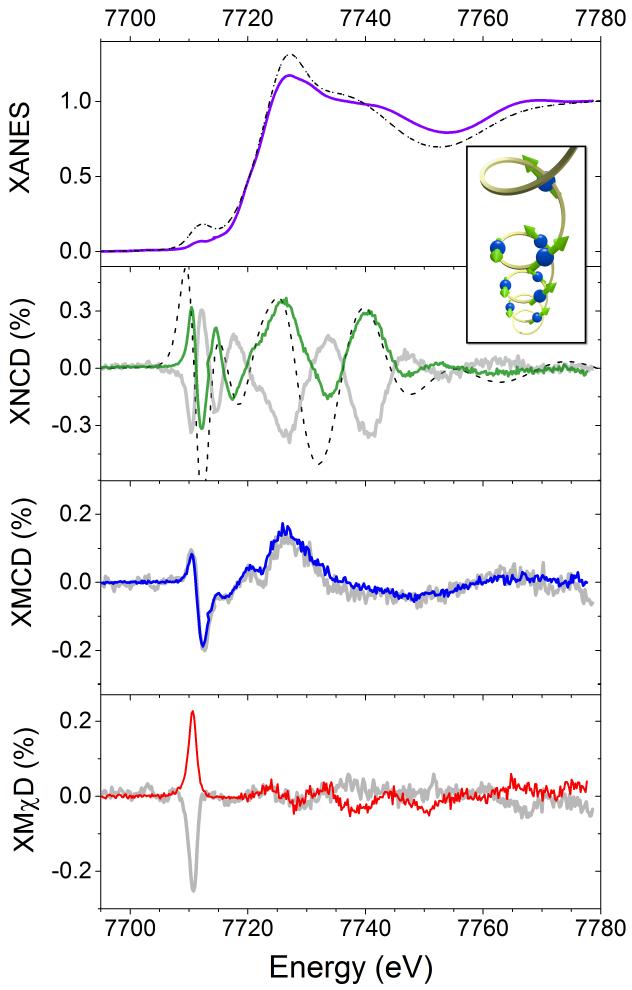
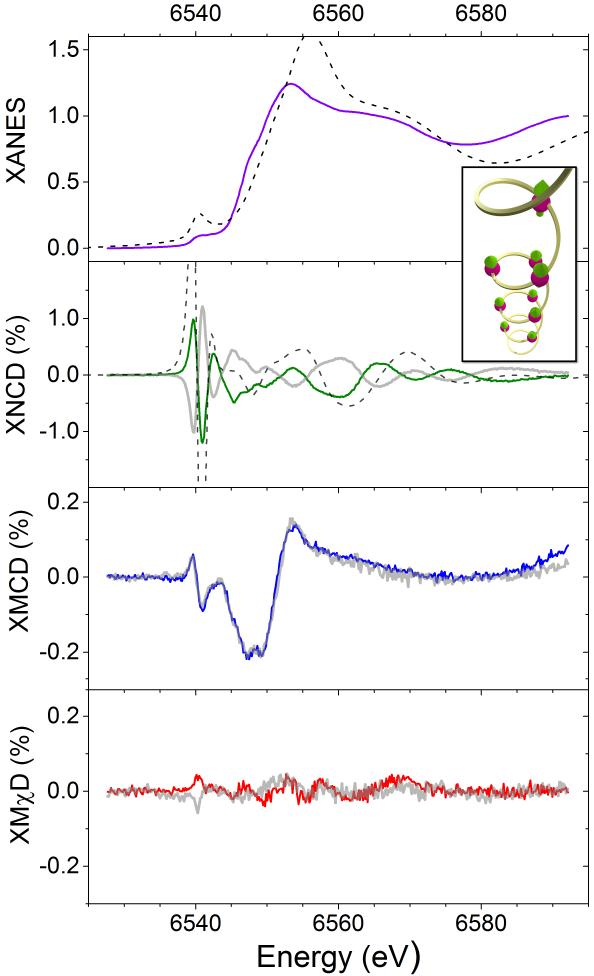
In Figure 2 the normalized absorption (XANES) spectrum and corresponding dichroic contributions, obtained according to eq. 1-3, are shown for two enantiomeric [Co-NIT]∞ crystals. The dichroic signals are normalized to the corresponding X-ray absorption edge jump. The results of similar experiments for the Mn derivatives are reported in Figure 3.
Figure 2. X-ray absorption and dichroic spectra of [Co-NIT]∞ helix.
X-ray near edge absorption spectra at the K-edge of Co measured at B=3 T and T=5 K. The dichroic contributions estimated according to equations (1-3), and expressed as the percentage of the edge jump in the absorption, are reported for two opposite enantiomers, the second one in pale grey for clarity. The dotted black lines correspond to the calculated XANES and XNCD for the P31 enantiomer, whose helicity is visible in the schematic structure drawn in the inset, with arrows representing the non-collinear spin structure of the Cobalt helix.
Figure 3. X-ray absorption and dichroic spectra of [Mn-NIT]∞ helix.
X-ray near edge absorption spectra at the K-edge of Mn measured at B=3 T and T=5 K. The dichroic contributions estimated according to equations (1-3), and expressed as the percentage of the edge jump in the absorption, are reported for two opposite enantiomers, the second one in pale grey for clarity. The black lines correspond to the calculated XANES and XNCD for the P31 enantiomer, whose helicity is visible in the schematic structure drawn in the inset, with arrows representing the collinear spin structure of the Manganese helix.
Figure 2 and 3 unambiguously show that the three detected dichroic signals, when compared for enantiomeric crystals, are in agreement with the symmetry properties reported in Table 1. Non-zero XNCD and XMχD signals are indeed compatible with the crystal symmetry. In fact the P31/P32 space groups are among the few ones exhibiting all magneto-electric effects, including the existence of toroidal (or anapole) moments.31,32 As magnetochiral dichroism is in general a weak phenomenon, whose intensity is evaluated as the difference of much larger quantities, the comparison of the three dichroic signals is mandatory. Given the fact that every dichroic signal reverses its sign according to parity and time-reversal symmetries of the involved optical transition (see Table 1), the presence of artefacts can be safely excluded.
Beyond parity effects, also the spectral features of the dichroic signals provide useful information. Natural circular dichroism is zero for any pure transition and could be observed in the X-ray range only via an interference E1E2 term. This contribution is non-zero only if the system has no inversion symmetry. Absence of inversion symmetry allows the atomic orbitals of different parity (e.g., p- and d-) to hybridize. In the case of absorption at the K-edge of transition metals, this corresponds to 3d-4p hybridization and the XNCD signal is in fact observed at the pre-edge, the feature at the low energy side of the absorption edge, of both [Co-NIT]∞ and [Mn-NIT]∞ helices, ca. 7710 eV and 6540 eV, respectively. Interestingly XNCD is significantly different from zero on a wide energy range, ca. 50 eV, for both [M-NIT]∞ systems. This implies a significant hybridization of extended states formed by empty orbitals (e.g. 4p-4d, 4d-5p, etc.) that is compatible with the low symmetry of the metal site induced by the ligands. Similar wide-energy XNCD features were also observed in NdIII 33 and NiII 34 compounds, in which the chirality is induced by the structural arrangement of non-chiral moieties, whereas the XMCD signal for a CoII complex with chiral coordination is present only in the pre-edge region where the 3d orbitals contribute predominantly.35
Both XANES and XNCD were reproduced by calculations performed using the FDMNES (Finite Difference Method Near-Edge Structure) package.36 The electronic structure around Co and Mn atoms were calculated using the multiple scattering theory within the muffin-tin approximation, based on a mono-electronic approach. Calculations were performed for clusters built from crystallographic data for P31 space group including hydrogen atoms and views of the asymmetric units generating the chain structure are provided in Supplementary Figure 1 together with a list of selected bond distances and angles (Supplementary Table 1). Natural circular dichroism was calculated considering E1E2 transitions only (see methods for details). The spectral features of both derivatives are reproduced with a reasonable agreement to assign unambiguously the P31 space group, whose chirality is shown in the inset of Figure 2 and 3, to the crystals having their spectra drawn in colour in the corresponding figure. XNCD intensity at the pre-edge is about twice larger for the [Mn-NIT]∞ helix, in agreement with the larger number of holes in the 3d orbitals and the larger calculated density-of-states (DOS) of the d-orbitals at the Fermi level, reported as Supplementary Figure 2.
Concerning XMCD, for which interference E1E2 contributions are forbidden by symmetry consideration, the dichroic signal is due to both the dipolar E1E1 (1s → 4p) transitions at the rising edge and to the quadrupolar E2E2 (1s→ 3d) transitions at the pre-edge part of the spectrum, where the partially occupied 3d orbitals are involved. Given the fact that the initial 1s state has no spin-orbit coupling, the XMCD at the K-edge is probing only orbital magnetization of the final states. For a d5 ion (MnII) K-edge XMCD at the pre-edge is thus expected to be much weaker than for the Co derivative. Comparing Figures 2 and 3 it is well evident that XMCD at the pre-edge is significantly reduced passing from Co to Mn, despite that the magnetization is higher in the latter. On the contrary, XMCD at the rising edge, which is originated by the orbital polarization of the 4p states, is fairly similar for the Co and Mn helices, as expected (see also the calculated p-type DOS in Supplementary Figure 2).
Finally, passing to X-ray magnetochiral dichroism, we notice that it originates from the same interference interaction terms as XNCD, though combined with the orbital magnetization of the final states of the absorbing atom. Here a significant difference is observed between the two systems. [Co-NIT]∞ helices exhibit a large XMχD signal whose intensity exceeds that of the XMCD signal. To allow a better comparison with data extracted from UV-visible spectroscopy the dichroic contributions are plotted as their correspondent Kuhn asymmetry, i.e. g=Δμ/μ, where μ is the absorption. The results are shown in the inset of Figure 4 and reveals that the magnetochiral effect exceeds 3% of the corresponding absorptions, thus a remarkable quantity compared to previous reported values. 17-21,37 For instance XMχD of [Co-NIT]∞ is two orders of magnitude stronger than what obtained from preliminary measurements at the K edge on a CrIII-NiII molecular ferromagnet34 or to that measured in absorption experiments in the UV-vis range on a ferromagnetically ordered CrIII-MnII molecular compound.19
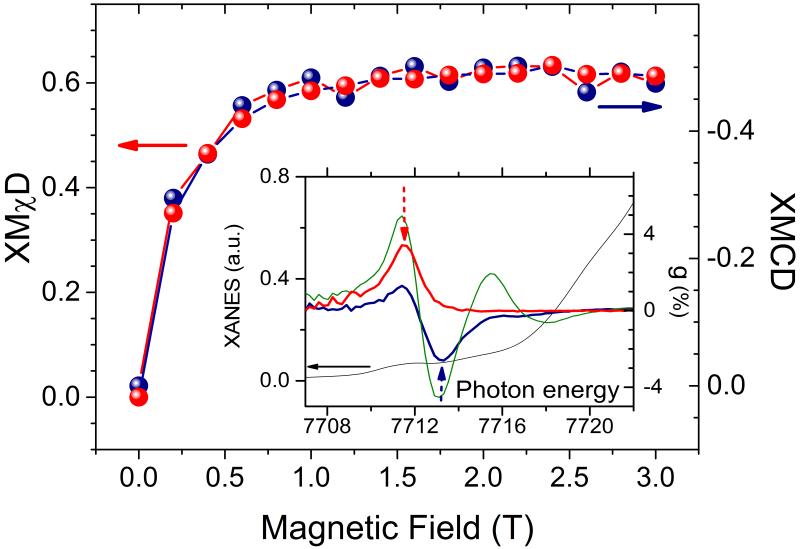
Figure 4. Field dependence of magnetic and magneto-chiral dichroism of the [Co-NIT]∞ helix.
XMχD (red dots) and XMCD (blue dots) measured at the photon energy of their maximum intensity (see inset) are reported as a function of the magnetic field applied at 15° from the c crystallographic axis at T=8 K. In the inset the photon energy dependence of the intensity of the dichroic contributions (XNCD in green, XMCD in blue, XMχD in red) are reported as the asymmetric ratio g=Δμ/μ, i.e. normalizing the signal to the absorption intensity at the same photon energy, which is assumed to be zero before the K-edge. The arrows indicate the photon energy used to record the field dependence of the corresponding dichroic signals.
As far as the spectral shape is concerned XMχD signal is absolutely different from the other dichroic contributions, showing a well-defined narrow peak around 7710 eV, i. e. at the pre-edge. This is nicely in agreement with qualitative expectations, being a quantitative analysis of this effect beyond currently available theoretical models. In fact, the intensity of the magneto-chiral contribution depends on the interference E1E2 term but also on the orbital magnetism of the final state that is significantly different from zero only where 4p orbitals are admixed with partially filled 3d orbitals, i.e. at the pre-edge, where the calculated DOS (see Supplementary Figure 2) reveals significant contribution of both type of orbitals. A dichroic signal extending on a wider spectral region is instead observed for XNCD due to hybridized extended empty orbitals like, for instance, 4p-4d, 4d-5p, etc.
Passing to the [Mn-NIT]∞ helix, Figure 3 reveals a dramatic decrease of the XMχD signal, which becomes hardly detectable. The intensity of XMχD is often assumed in the literature to be proportional to the product of natural and magnetic dichroism38 but a rigorous general treatment has not yet been developed. Our element selective experiments clearly show the limited validity of this assumption in the hard X-ray range.
In order to get a deeper understanding of this phenomenon, we have also checked how XMCD and XMχD depends on the extent of magnetization of the absorbing atoms by performing the experiment on the [Co-NIT]∞ helix as a function of applied magnetic fields in the range 0 - 3 T at T=8 K, thus above the freezing temperature of the magnetization of this slow relaxing material. The field dependence of the maximum signal, measured at 7713.2 and 7711.5 eV for XMCD and XMχD, respectively, is reported in Figure 4. The experiment unambiguously reveals that the two dichroic contributions have exactly the same field dependence, suggesting that the magnetization of the absorbing atoms enters directly in the magneto-chiral effect.
It is interesting to frame our results in the current knowledge of this relatively recent and still unexplored magneto-optical effect. Here all chiral contributions to X-ray absorption spectra are simultaneously detected and their lineshape are analysed. Moreover we have found that magnetochiral dichroism at the Co K-edge is as large as the other dichroic contributions. A very large XMχD, g~1% at room temperature, has been recently reported for a chiral paramagnetic molecule comprising Terbium(III) and Nickel(II) atoms.21 Surprisingly, the effect was detected only at the L3-edge of Tb, despite that no symmetry reasons should hamper its observation at the L2-edge. This clearly shows how elusive the detection of the magnetochiral effect can be and underlines the relevance of a complete characterization as the one presented here.
Additional information can be extracted by the unprecedented possibility to compare the magnetochiral behaviour of two isostructural 1D systems showing very different magnetic properties. First of all it is well evident that the asymmetry factor of the magnetochiral effect in this energy range is not simply the product of the natural and magnetic ones, because in this approximation a large signal should be observed over a wide energy range and much stronger XMχD should be observed for [Mn-NIT]∞. In addition the XMχD signal is only significant for transitions involving 3d partially filled orbitals and only in the presence of a strong orbital contribution, as in the case of a d7 ion in octahedral environment, which is responsible of the non-collinear spin arrangement along the helix of the [Co-NIT]∞ helix.
It would be interesting to investigate if the three-fold screw axis generating the molecular [M-NIT]∞ helices plays a significant role in the large magnetochiral dichroism observed here. Other chains comprising the same building blocks and differing only for the organic group on the radical, aliphatic instead of aromatic (see Supplementary Figure 3), have been structurally and magnetically characterized but unfortunately all of them crystallize in centrosymmetric space groups.39 However, thanks to the element selectivity of the X-ray absorption, it has been possible to compute the XNCD of acentric mixed-metal structures artificially segregating Co and Mn on sites of opposite parity compared to the inversion centre (see Supplementary Figure 4 and Supplementary Note 1). The results, obtained using the previously described computational approach, reveal a significant decrease to ca. 1/3 of the XNCD calculated signal when passing from the P31/P32 to the P21 crystal space group, as shown in Supplementary Figure 5. As the trigonal space group of the investigated helices is induced by the π-stacking interactions between the aromatic substituent on the radical and the hfac ligand on the metal,39 a route to enhance the magnetochiral effect in molecular materials through a rational chemical design can be envisaged.
In conclusion, the investigated magnetic molecular helices results to be a model system to study in detail the magnetochiral effect. The symmetry of the material is compatible with a large variety of magneto-electric effects,22,23,40 still poorly investigated in molecular materials. According to sum rules41,42 the X-ray magnetochiral dichroism could be associated with the presence of atomic anapole orbital moment, ΩL, originated from toroidal orbital currents centred on the Cobalt atoms. These orbital currents, of relevance for many phenomena ranging from multiferroicity35 to superconductivity,43 originate from the hybridized 3d-4p states, allowed by the absence of inversion symmetry of the coordination environment around the atom, and therefore they are much stronger that what one would expect for those induced by the parity breaking due to the electroweak interaction. It is important to underline that this atomic anapole orbital moment should not be confused with the macroscopic toroidal moment27 that could originate from the peculiar non collinear orientation of the magnetic moments along the three-fold helix, which is compatible with Dzyaloshinskii-Moriya interactions. To investigate this additional contribution a less local probe, i.e. UV-visible light, is however necessary. Last but not least we recall that the [Co-NIT]∞ molecular helix presents the additional feature of magnetic bistability in the paramagnetic phase. This systems seems therefore a good candidate for the detection of the “inverse” magnetochiral effect, i.e. the induction of magnetic polarization in a chiral system by irradiation with non-polarized light. In the scenario of light-matter interaction, this effect, although theoretically predicted,44 is the one still not evidenced by experiments.40 The possibility to freeze at low temperature the light induced magnetization of this bistable molecular material should facilitate the detection of a weak inverse magnetochiral effect.
METHODS
Crystals of [Mn(hfac)2NITPhOMe]∞ and [Co(hfac)2NITPhOMe]∞ were prepared as previously reported.24,39 Single crystals with needle shape of largest dimension of ca. 10×0.5×0.5 mm3 were selected and checked for absence of twinning with an Oxford Diffraction single crystal diffractometer.
The X-ray absorption experiments were carried out at the ID12 beamline of the European Synchrotron Radiation Facility (ESRF), which is dedicated to polarization dependent X-ray spectroscopy in the photon energy range from 2 to15 keV.45 For the experiments at the Mn and Co K-edge the source was the helical undulator APPLE-II which provides a high flux of either right or left circularly polarized x-rays photons with polarization rate in excess of 0.95. The helicity could be changed in a time less than 5 seconds. X-rays were monochromatized by the Si <111> double crystal monochromator ensuring the energy resolution better than the intrinsic broadening due to the finite core-hole lifetime. The samples were mounted on a cold finger of a constant flow Helium cryostat inserted in a bore of superconducting solenoid producing a magnetic field up to 17 Tesla. The sweep rate to reverse the direction of magnetic field rate was 2 T/min. All spectra were recorded in total X-ray fluorescence detection mode in backscattering geometry using Si photodiodes. Total X-ray fluorescence signal in this energy range is expected to be isotropic. Either the helicity of the incoming X-rays or the direction of magnetic field were changed after each consecutive energy scans to minimize any eventual artefacts in the measurements.
The XANES and XNCD spectra using FDMNES code.36 Calculations were performed for clusters built from crystallographic data for P31 space group including hydrogen atoms. Crystallographic data are available through the Cambridge Structural Database (http://www.ccdc.cam.ac.uk/Community/Requestastructure/Pages/Requestastructure.aspx) using the doi codes 10.1021/ic00020a029 and 10.1039/B004244G for Mn and Co derivatives, respectively. Natural circular dichroism was calculated considering E1E2 transitions only. Self-consistent calculations including relativistic effects were also performed and similar results were obtained. Clusters of radius of 14 Å were employed to reproduce the main features in the XNCD, as a further increase of the cluster size did not lead to any improvement. The same procedure was repeated for an aliphatic radical analogue46 crystallizing in the centrosymmetric P21/c space group (doi n° 10.1021/ic00283a018 to retrieve crystallographic data from the database mentioned above) by replacing the Mn atoms on the screw axis of opposite chirality, generated by the inversion centre, with Co atoms. The structural similarity between the Mn and Co derivatives and their complete miscibility to form mixed species suggest that no significant structural stress is induced in this artificial model. The spectra were convoluted to a Lorentzian, with an energy dependent width to take into account the core-hole lifetime, with a Gaussian line to account for the energy resolution of monochromator. The calculated absorption cross sections were normalized to the same edge jump to the continuum as in the experiment.
Supplementary Material
Acknowledgments
We acknowledge the financial contribution of the European Research Council through the AdG MolNanoMaS (267746). The support of ESRF through beamtime allocation (projects HE-3896 and HC-972). We are indebted to Y. Joly for assistance in the spectra simulation and to R. Caciuffo, Ph. Sainctavit, and J. Villain for stimulating discussions.
References
- 1.Pasteur L. La dissymétrie moléculaire. Conférence faite le 22 décembre 1883. Rev. Sci. 1884;7:2–6. [Google Scholar]
- 2.Bordacs S, et al. Chirality of matter shows up via spin excitations. Nature Phys. 2012;8:734–738. [Google Scholar]
- 3.Mühlbauer S, et al. Skyrmion lattice in a chiral magnet. Science. 2009;323:915–919. doi: 10.1126/science.1166767. [DOI] [PubMed] [Google Scholar]
- 4.Fert A, Cros V, Sampaio J. Skyrmions on the track. Nat. Nanotechnol. 2013;8:152–156. doi: 10.1038/nnano.2013.29. [DOI] [PubMed] [Google Scholar]
- 5.Romming N, et al. Writing and deleting single magnetic skyrmions. Science. 2013;341:636–639. doi: 10.1126/science.1240573. [DOI] [PubMed] [Google Scholar]
- 6.Pop F, Auban-Senzier P, Canadell E, Rikken GLJA, Avarvari N. Electrical magnetochiral anisotropy in a bulk chiral molecular conductor. Nat. Commun. 2014;5 doi: 10.1038/ncomms4757. doi:10.1038/ncomms4757. [DOI] [PubMed] [Google Scholar]
- 7.Wagnière G, Meier A. The influence of a static magnetic field on the absorption coefficient of a chiral molecule. Chem. Phys. Lett. 1982;93:78–81. [Google Scholar]
- 8.Groenewege MP. A theory of magneto-optical rotation in diamagnetic molecules of low symmetry. Mol. Phys. 1962;5:541–563. [Google Scholar]
- 9.Barron LD, Vrbancich J. Magneto-chiral birefringence and dichroism. Mol. Phys. 1984;51:715–730. [Google Scholar]
- 10.Baranova NB, Bogdanov YV, Zel’Dovich BY. Electrical analog of the Faraday effect and other new optical effects in liquids. Opt. Commun. 1977;22:243–247. [Google Scholar]
- 11.Rikken G, Raupach E. Observation of magneto-chiral dichroism. Nature. 1997;390:493–494. [Google Scholar]
- 12.Goulon J, et al. X-ray magnetochiral dichroism: A new spectroscopic probe of parity nonconserving magnetic solids. Phys. Rev. Lett. 2002;88:237401. doi: 10.1103/PhysRevLett.88.237401. [DOI] [PubMed] [Google Scholar]
- 13.Wagnière GH. On chiralty and the universal asymmetry. Verlag Helvetica Chimica Acta; 2007. [Google Scholar]
- 14.Guijarro A, Yus M. The origin of chirality in the molecules of life. Royal Society of Chemistry; 2009. [Google Scholar]
- 15.Rikken GLJA, Raupach E. Enantioselective magnetochiral photochemistry. Nature. 2000;405:932–935. doi: 10.1038/35016043. [DOI] [PubMed] [Google Scholar]
- 16.Zel’dovich YB. Electromagnetic interaction with parity violation. Sov. Phys. JETP. 1958;6:1184. [Zh. Eksp. Teor. Fiz. 1133, 1531 (1957)] [Google Scholar]
- 17.Vallet M, et al. Observation of magnetochiral birefringence. Phys. Rev. Lett. 2001;87:183003. [Google Scholar]
- 18.Kubota M, et al. X-Ray directional dichroism of a polar ferrimagnet. Phys. Rev. Lett. 2004;92:137401. doi: 10.1103/PhysRevLett.92.137401. [DOI] [PubMed] [Google Scholar]
- 19.Train C, et al. Strong magneto-chiral dichroism in enantiopure chiral ferromagnets. Nat. Mater. 2008;7:729–734. doi: 10.1038/nmat2256. [DOI] [PubMed] [Google Scholar]
- 20.Kitagawa Y, Segawa H, Ishii K. Magneto-chiral dichroism of organic compounds. Angew. Chem. Int. Ed. Engl. 2011;50:9133–9136. doi: 10.1002/anie.201101809. [DOI] [PubMed] [Google Scholar]
- 21.Ceolín M, Goberna-Ferrón S, Galán-Mascarós JR. Strong hard X-ray magnetochiral dichroism in paramagnetic enantiopure molecules. Adv. Mater. 2012;24:3120–3123. doi: 10.1002/adma.201200786. [DOI] [PubMed] [Google Scholar]
- 22.Cheong S-W, Mostovoy M. Multiferroics: a magnetic twist for ferroelectricity. Nat. Mater. 2007;6:13–20. doi: 10.1038/nmat1804. [DOI] [PubMed] [Google Scholar]
- 23.Khomskii D. Classifying multiferroics: Mechanisms and effects. Physics. 2009;2:20. [Google Scholar]
- 24.Caneschi A, Gatteschi D, Rey P, Sessoli R. Structure and magnetic-ordering of a ferrimagnetic helix formed by manganese(II) and a nitronyl nitroxide radical. Inorg. Chem. 1991;30:3936–3941. [Google Scholar]
- 25.Caneschi A, et al. Cobalt(II)-nitronyl nitroxide chains as molecular magnetic nanowires. Angew. Chem. Int. Ed. Engl. 2001;40:1760–1763. doi: 10.1002/1521-3773(20010504)40:9<1760::aid-anie17600>3.0.co;2-u. [DOI] [PubMed] [Google Scholar]
- 26.Cavigli L, Sessoli R, Gurioli M, Bogani L. Second harmonic generation in a molecular magnetic chain. Phys. Status Solidi A. 2006;203:1402–1408. [Google Scholar]
- 27.Heintze E, et al. Dynamic control of magnetic nanowires by light-induced domain-wall kickoffs. Nat. Mater. 2013;12:202–206. doi: 10.1038/nmat3498. [DOI] [PubMed] [Google Scholar]
- 28.Glauber RJ. Time-dependent statistic of the ising model. J. Math. Phys. 1963;4:294–307. [Google Scholar]
- 29.Bogani L, et al. Finite-size effects in single chain magnets: an experimental and theoretical study. Phys. Rev. Lett. 2004;92:207204. doi: 10.1103/PhysRevLett.92.207204. [DOI] [PubMed] [Google Scholar]
- 30.Goulon J, et al. X-ray optical activity: Applications of sum rules. JETP. 2003;97:402–431. [Google Scholar]
- 31.Spaldin N,A, Fiebig M, Mostovoy M. The toroidal moment in condensed-matter physics and its relation to the magnetoelectric effect. J. Phys.: Condens. Matter. 2008;20:434203. [Google Scholar]
- 32.Szaller D, Bordács S, Kézsmárki I. Symmetry conditions for nonreciprocal light propagation in magnetic crystals. Phys. Rev. B. 2013;87:014421. [Google Scholar]
- 33.Alagna L, et al. X-Ray natural circular dichroism. Phys. Rev. Lett. 1998;80:4799–4802. [Google Scholar]
- 34.Goulon J, Rogalev A, Brouder C. Comprehensive chiroptical spectroscopy. John Wiley & Sons, Inc.; 2012. pp. 457–491. [Google Scholar]
- 35.Stewart B, et al. Circular dichroism at the edge: Large X-ray natural CD in the 1s → 3d pre-edge feature of 2[Co(en)3Cl3]·NaCl·6H2O. J. Am. Chem. Soc. 1999;121:10233–10234. [Google Scholar]
- 36.Bunău O, Joly Y. Self-consistent aspects of x-ray absorption calculations. J. Phys.: Condens. Matter. 2009;21:345501. doi: 10.1088/0953-8984/21/34/345501. [DOI] [PubMed] [Google Scholar]
- 37.Kitagawa Y, Miyatake T, Ishii K. Magneto-chiral dichroism of artificial light-harvesting antenna. Chem. Commun. 2012;48:5091–5093. doi: 10.1039/c2cc30996c. [DOI] [PubMed] [Google Scholar]
- 38.Rikken G, Raupach E. Pure and cascaded magnetochiral anisotropy in optical absorption. Phys. Rev. E. 1998;58:5081–5084. [Google Scholar]
- 39.Caneschi A, Gatteschi D, Lalioti N, Sangregorio C, Sessoli R. Supramolecular interactions and magnetism of metal-radical chains. J. Chem. Soc. Dalton Trans. 2000:3907–3912. [Google Scholar]
- 40.Kibayashi S, Takahashi Y, Seki S, Tokura Y. Magnetochiral dichroism resonant with electromagnons in a helimagnet. Nat. Commun. 2014;5:4583. doi: 10.1038/ncomms5583. doi: 10.1038/ncomms5583. [DOI] [PubMed] [Google Scholar]
- 41.Carra P, Jerez A, Marri I. X-ray dichroism in noncentrosymmetric crystals. Phys. Rev. B. 2003;67:045111. [Google Scholar]
- 42.Lovesey SW, Balcar E. Quantum theory of natural circular,magnetoc-chiral, and non-reciprocal linear dichroism. Phys. Scr. 2010;81:065703. [Google Scholar]
- 43.Scagnoli V, et al. Observation of Orbital Currents in CuO. Science. 2011;332:696–698. doi: 10.1126/science.1201061. [DOI] [PubMed] [Google Scholar]
- 44.Wagnière G. Inverse magnetochiral birefringence. Phys. Rev. A. 1989;40:2437–2440. doi: 10.1103/physreva.40.2437. [DOI] [PubMed] [Google Scholar]
- 45.Rogalev A, Goulon J, Goulon-Ginet C, Malgrange C. In: Magnetism and synchrotron radiation. Beaurepaire E, Scheurer F, Krill G, Kappler JP, editors. Vol. 61. Springer-Verlag; 2001. (Lecture notes in physics). [Google Scholar]
- 46.Caneschi A, Gatteschi D, Rey P, Sessoli R. Structure and magnetic-properties of ferrimagnetic chains formed by manganese(II) and nitronyl nitroxides. Inorg. Chem. 1988;27:1756–1761. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.