Abstract
Motivation: The distribution of allele frequencies across polymorphic sites, also known as the site frequency spectrum (SFS), is of primary interest in population genetics. It is a complete summary of sequence variation at unlinked sites and more generally, its shape reflects underlying population genetic processes. One practical challenge is that inferring the SFS from low coverage sequencing data in a straightforward manner by using genotype calls can lead to significant bias. To reduce bias, previous studies have used a statistical method that directly estimates the SFS from sequencing data by first computing site allele frequency (SAF) likelihood for each site (i.e. the likelihood a site has each possible allele frequency conditional on observed sequence reads) using a dynamic programming (DP) algorithm. Although this method produces an accurate SFS, computing the SAF likelihood is quadratic in the number of samples sequenced.
Results: To overcome this computational challenge, we propose an algorithm, ‘score-limited DP’ algorithm, which is linear in the number of genomes to compute the SAF likelihood. This algorithm works because in a lower triangular matrix that arises in the DP algorithm, all non-negligible values of the SAF likelihood are concentrated on a few cells around the best-guess allele counts. We show that our score-limited DP algorithm has comparable accuracy but is faster than the original DP algorithm. This speed improvement makes SFS estimation practical when using low coverage NGS data from a large number of individuals.
Availability and implementation: The program will be available via a link from the Novembre lab website (http://jnpopgen.org/).
Contact: ehan416@gmail.com, jnovembre@uchicago.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 Introduction
A site frequency spectrum (SFS) describes the distribution of allele frequencies across sites in the genome of a particular species. The SFS is of primary interest in population genetics, as it is a complete summary of sequence variation at unlinked sites and its shape reflects underlying population genetic processes, such as growth, bottlenecks and selection. Moreover, a number of population genetic inferences can proceed directly from the SFS. For example, demographic history (e.g. evidence for population expansions, bottlenecks or migrations) can be directly inferred from the SFS [using, for example, dadi (Gutenkunst et al., 2009) or (Excoffier et al., 2013)]. The SFS can also be compressed down to univariate summary statistics that form the basis of popular neutrality tests (Achaz, 2008, 2009; Fay and Wu, 2000; Fu and Li, 1993; Tajima, 1989) that underlie many empirical genome-wide selection scans (e.g. Andolfatto, 2007; Begun et al., 2007). Hence, inferring the precise SFS from genetic data is crucial in many population genetic analyses.
With the recent rapid progress in sequencing techniques, obtaining large-scale genomic data from thousands to tens of thousands of individuals is practical (e.g. 1000 Genomes Project Consortium, 2010, 2012; Fu et al., 2013; Nelson et al., 2012) and this increased sample size enables us to conduct more accurate population genetic inference. However, current massively parallel short-read sequence technologies also pose many inherent challenges—for example, reads have high error rates, read mapping is sometimes uncertain and coverage is variable and in many cases low or completely absent. These challenges make accurate individual-level genotype calls difficult and make some downstream analysis based on the inferred genotypes problematic.
In a previous study (Han et al., 2014), we showed that the SFS computed from genotype calls (a call-based estimation approach) is biased at low to medium coverage (≤10×), whereas the SFS directly inferred from aligned short-read sequencing data (a direct estimation approach) is unbiased even at low coverage. The direct estimation approach infers the maximum likelihood estimate (MLE) of the SFS by an EM algorithm (Li, 2011) or a Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm (Nielsen et al., 2012), assuming independence across all individuals and sites. Both of these algorithms are implemented in the ANGSD software package (Nielsen et al., 2012).
Both of these algorithms require computation of the site allele frequency (SAF) likelihood for all sites. These vectors contain the likelihood that an allele for each possible allele frequency at a site (regardless whether monomorphic or polymorphic) conditional on observed sequence reads. Based on the precomputed SAF likelihoods, the MLE of the SFS is obtained by optimization, using either the EM (Li, 2011) or the BFGS algorithm (Nielsen et al., 2012). The bottleneck in obtaining the MLE of the SFS is computing the SAF likelihoods, rather than optimization. In fact, the maximization of the likelihood either by the EM or the BFGS algorithm takes only a small fraction of time compared with the computation of the SAF likelihood. This is because computation of the SAF likelihood at each site requires a summation over all possible genotype combinations for n individuals and naive computation of this sum has a runtime complexity of . To overcome this computational burden, Li (2011) proposed a dynamic programming (DP) algorithm to effectively compute the SAF likelihood for each site in and Nielsen et al. (2012) implemented this algorithm in the ANGSD software. However, this algorithm is still not practical to use if there are large numbers of individuals, because it is quadratic in the number of genomes (see Fig. 1B for runtime). Moreover, this algorithm is numerically unstable for a large sample (Li, 2011). To solve this problem of computational inefficiency and numerical instability, we compute the SAF likelihood in a more efficient way that still retains the accuracy of the original DP algorithm. Our new method uses a combination of rescaling and sensible approximation to compute the SAF likelihood.
Fig. 1.
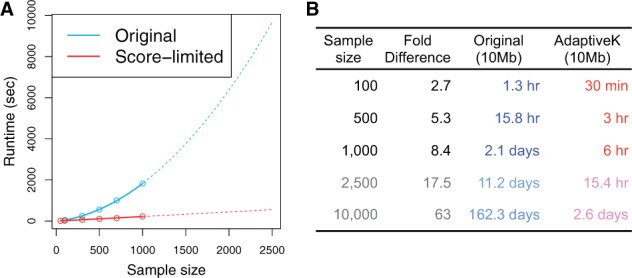
Runtime comparisons for updating the SAF likelihood by two different algorithms (Original and Score-limited). The sequencing data were simulated at coverage 3×, 5× and 10× with the error rate of 0.001 and the sample size of 50, 100, 300, 500, 750 and 1000. Note that experiments are only performed with , and the results for (the dotted line in A and the last two rows of B) are extrapolated from the results with
2 Approach
To establish notation and background, we first review the existing DP algorithm implemented in the ANGSD software (Nielsen et al., 2012) and then introduce our approach.
2.1 DP algorithm used by ANGSD
Let D denote the short-read sequencing data and X represent a total count of the derived allele for a sample of n diploid individuals at a particular site. The corresponding SAF likelihood, , is a -dimensional vector in which each element, , is the likelihood that the derived allele frequency in the sample is :
| (1) |
where is an indicator function and is a genotype likelihood of the individual k for genotype gk.
To calculate the SAF likelihood h by the DP algorithm, define a raw SAF likelihood for j individuals (-dimensional vector), given by , in which each element is defined as
| (2) |
where and . Note that this expression does not include a rescaling factor .
The vector is iteratively updated from the vector (raw SAF likelihood for j – 1 individuals) by the following recurrence relation:
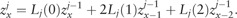 |
(3) |
In a final step, each element of the vector is rescaled by a corresponding factor to obtain the vector
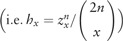 , and then the resulting vector is standardized such that the maximum element of the vector becomes 1, as likelihoods need only be defined proportional to a constant.
, and then the resulting vector is standardized such that the maximum element of the vector becomes 1, as likelihoods need only be defined proportional to a constant.
To illustrate the procedure, we show how the raw SAF likelihood is recursively updated from to by the DP algorithm in the ANGSD software. Each row in a lower triangular matrix in Figure 2A (top) represents the raw SAF likelihood for j individuals (a vector of length ). Figure 2A also shows how the raw SAF likelihood (middle) is converted to the final SAF likelihood (bottom) after rescaling by and standardization.
Fig. 2.
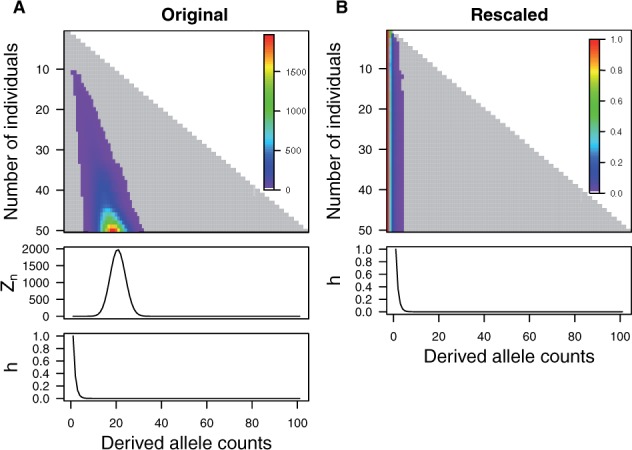
Updating the SAF likelihood for 50 diploid individuals at a particular site fixed for an ancestral allele by the original (A) or the rescaled (B) DP algorithm. The sequencing data were simulated at coverage 3× with sequencing error rate of 0.001. Genotype likelihoods were calculated using a Genome Analysis Tool Kit model (DePristo et al., 2011). (A) Top row shows how the raw SAF likelihood is recurrently updated by the original DP algorithm. Each row in a low triangular matrix represents the raw SAF likelihood for j individuals (). The value of the SAF likelihood is shown in a color scale, of which the range goes from 0 to 2000. Middle and bottom rows show how the raw SAF likelihood (the last row of the lower triangular matrix) is converted to the final SAF likelihood by rescaling and standardization. Note that the final SAF likelihood has a peak at the derived allele count of 0. (B) Top row shows how the rescaled SAF likelihood is recurrently updated by the rescaled DP algorithm. Each row in the lower triangular matrix represents the rescaled SAF likelihood for j individuals. The value of the SAF likelihood is shown in a color scale, of which the range goes from 0 to 1. Bottom row shows the final SAF likelihood . In both (A) and (B), the gray area represents the range of values computed by the original and the rescaled DP algorithm. In this example, it requires computation of 2600 elements (because ) to update the SAF likelihood
2.2 Rescaled DP algorithm
In our preliminary work, we observed that the value at the mode of can be relatively large. In this example with 50 diploid individuals, the mode of is 1973. With 500 diploid individuals, the mode of can be about (data not shown). This implies that the DP algorithm can have an arithmetic overflow problem (i.e. a computed value is greater in magnitude than the largest value that a computer can store in memory) for large samples because the mode of increases exponentially as the sample size increases. Furthermore, the values at the edges of are very small. In this example with 50 individuals, the value of the SAF likelihood function for the derived allele count of 100 is . With 500 diploid individuals, the value of the SAF likelihood function for the derived allele count of 1000 is smaller than (data not shown). This implies that the DP algorithm can have an arithmetic underflow problem (i.e. a computed value is smaller in magnitude than the smallest value that a computer can store in memory) for large samples because the values at the edges of keep decreasing exponentially as sample size increases. Therefore, the original DP algorithm will be numerically unstable for large samples, as the computation of creates both numerical overflow (at the mode of ) and underflow (away from the mode).
To overcome the numeric instability of the DP algorithm, we modified the original DP algorithm such that rescaling and standardization take place at each step of updating the SAF likelihood. For this modified algorithm, we define a rescaled SAF likelihood for j individuals (-dimensional vector), , of which each element is defined as
| (4) |
where and . We can derive a recurrence relation to iteratively update the vector from the vector (rescaled SAF likelihood for j – 1 individuals) as follows:
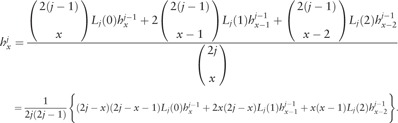 |
(5) |
Because the constant in Equation (5) is cancelled out during standardization, we can use the following recurrence equation to update the rescaled SAF likelihood:
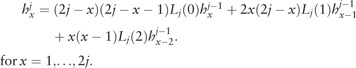 |
(6) |
Figure 2B shows how the SAF likelihood is recurrently updated from to by the rescaled DP algorithm in a lower triangular matrix (Figure 2B, top) and the final SAF likelihood (Figure 2B, bottom). Now, all values in the SAF likelihood range between 0 and1, suggesting there will be no potential numerical overflow. Importantly, we observed that the most of the cells in the SAF likelihood during update have a value close to 0 (shown in gray). This implies that computing all values of the SAF likelihood is inefficient and we can accurately approximate this vector by only computing the first few elements and setting the rest of the elements to 0. This motivated the development of the banded and score-limited DP algorithm.
2.3 Banded and score-limited DP algorithm
We observed that all non-negligible values of the updated rescaled SAF likelihoods, to , are consistently concentrated on the best-guess allele counts (Figure 2 for the allele frequency of 0 and Figure 3 for the allele frequency of 0.7). For example, for a site that is fixed for the ancestral allele, we observe that all non-negligible values of the rescaled SAF likelihoods are consistently observed on the first few cells of the vector, and the final SAF likelihood has a peak at the allele frequency of 0 (Fig. 2B). For a site that is polymorphic, we observe that the mode of the SAF likelihood typically stays at 0 when we add an individual whose best-guess genotype is 0/0 (i.e. the genotype likelihood vector of that individual has the highest value at genotype 0/0), whereas the mode typically moves to the right when we add an individual whose best-guess genotype is 0/1 or 1/1 (Fig. 3B). If we add an individual whose best-guess genotype is 0/1, the mode tends to move one bin to the right and the best-guess allele count increases by 1. By the same token, if we add an individual whose best-guess genotype is 1/1, the mode moves two bins to the right and the best-guess allele count increases by two.
Fig. 3.
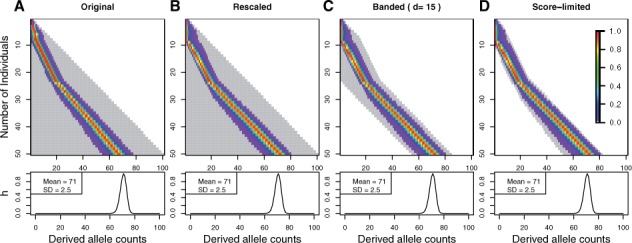
Updating the SAF likelihood for 50 diploid individuals by the original DP (A, referred to as Original), the rescaled DP (B, referred to as Rescaled), the banded DP (C, referred to as Banded) and the score-limited DP (D, referred to as score-limited) algorithm. The sequencing data were simulated at coverage 3× with error rate of 0.001. A random site with the true derived allele frequency of 0.7 is chosen. Each row in the lower triangular matrix represents the intermediate SAF likelihood for j individuals. The gray area represents the range of values computed by all four algorithms. Note that for the original DP algorithm, we standardized each row of the lower triangular matrix such that the maximum elements are assigned to one to compare with other three algorithms
Based on these observations, we propose a new algorithm, called a banded DP algorithm, which can compute the SAF likelihood in a more efficient manner than the original DP algorithm, but with good approximation to the SAF likelihood computed by the original DP algorithm (Fig. 3C). When updating the SAF likelihood (i.e. filling in each row of the lower triangular matrix), this algorithm finds the most likely position for the mode, and only updates values of the SAF likelihood d bins away from that position in both directions and sets the rest of the values zero. Here d represents a user defined bandwidth.
Let GCj denote the number of derived allele in the best-guess genotype for individual j () and ACj the best-guess allele count for j individuals. For each row of the lower triangular matrix, the banded DP algorithm computes the number of derived allele in the best-guess genotype (GCj) based on the genotype likelihoods of a given individual, and then updates the best-guess allele count (ACj) using the best-guess genotype:
where . Next, it computes the values of the SAF likelihood only within d bins away from the best-guess allele count (ACj) in both directions and outside of which it sets the values of the SAF likelihood to zero—i.e. is computed by Equation (5) if and otherwise . By doing so, the SAF likelihood is updated in a banded-fashion (computing at most values at each updating step, where d is a uniform bandwidth) rather than updated in a triangular fashion (computing values). This makes computation time close to O(dn) rather than the original .
Our algorithm has connections with existing banded DP algorithms (for example, banded Needleman-Wunsch alignment algorithm and banded Smith–Waterman alignment algorithm) (Sung, 2009). The banded DP algorithm fills in only the middle part of the DP matrix in a banded fashion (with band length of ), and does not compute the lower and upper triangles in the matrix. However, unlike existing banded DP algorithms, we need to repeat the same process across all sites and we realized that using the uniform value of band length d across all site does not work in practice due to site-to-site variability of the SAF likelihood (see Fig. 4B). Moreover, around the best-guess allele count, the number of values we need to compute is not usually symmetric in the left and right sides, implying that using the same band length for both sides is not efficient. Therefore, we propose another new algorithm, called a score-limited DP algorithm. This algorithm is different from the banded DP algorithm in a way that the number of cells to be computed at each updating step is adaptively changed rather than being kept at a uniform band length ().
Fig. 4.
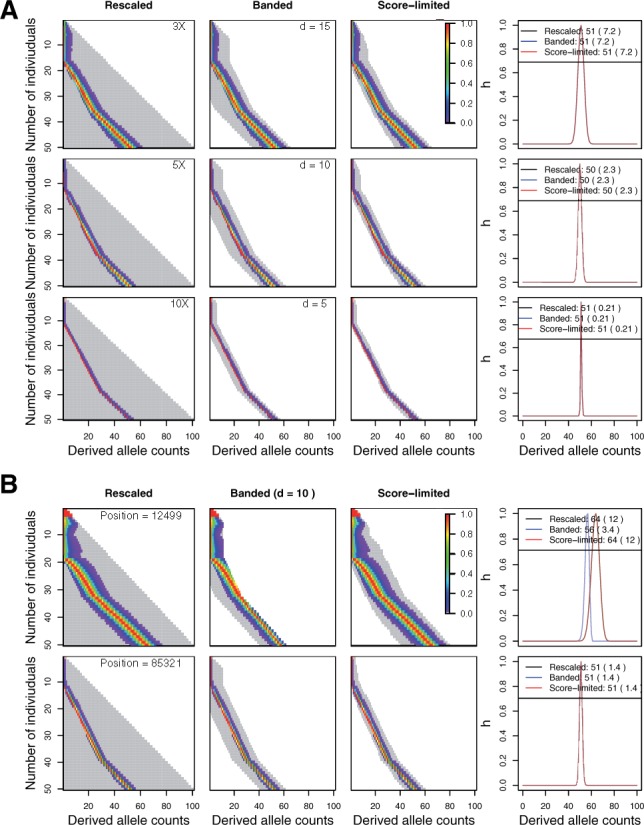
Performance of the three algorithms (Rescaled, Banded and Score-limited) for updating the SAF likelihood with simulated sequencing data (A) and real data (B). (A) It shows how the SAF likelihood is updated for 50 individuals as a function of sequencing coverage in simulated sequencing data. The sequencing data were simulated at coverage 3× (top), 5× (middle) and 10× (bottom) with error rate of 0.001, and a site with the true allele frequency of 0.51 is randomly picked. Each row of the lower triangular matrix represents the SAF likelihood vector for j individuals, and the gray area represents the range of values computed by each algorithm. The final SAF likelihood by all three algorithms is shown in black (Rescaled), blue (Banded), and red (Score-limited). Note that all three distributions almost completely overlap, and the mean and variance are the same for all three distributions. (B) It shows how the SAF likelihood is updated for 50 GBR individuals in the 1000 Genome Project at two random sites with the same best-guess allele frequency of 0.5. Two sites (top for position 10 085 321 and bottom for position 10 012 499 in chromosome 10) have the different variance of the SAF likelihood
Our score-limited DP algorithm also starts from computing the number of derived allele in the best-guess genotype based on the genotype likelihoods of a given individual. Then, it proposes left and right boundaries within which we update values of the SAF likelihood. Let Lj and Rj denote the left and right boundaries, respectively, within which we update the SAF likelihood for j individuals (). It updates the left and right boundaries using the best-guess genotype:
For example, for the individuals whose best-guess genotype is 0/0 we do not change the boundaries (). For individuals whose best-guess genotype is 0/1 we move both boundaries one bin to the right (), and for the individuals whose best-guess genotype is 1/1 we move both boundaries two bins to the right ().
Next, it checks whether a value at the left boundary (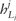 ) is greater than a very small value ϵ (for example, we set ) and if so, it expands the appropriate boundary to the left until the value at the updated left boundary is less than or equal to ϵ. By the same token, it checks the value at the right boundary () and if the value is greater than ϵ, then it expands the right boundary to the right until the value at the updated right boundary is less than or equal to ϵ. Finally, it computes the values of the SAF likelihood only within the left and right boundaries and outside of which we set the values of the SAF likelihood to zero—i.e. is computed by Equation (5) if
) is greater than a very small value ϵ (for example, we set ) and if so, it expands the appropriate boundary to the left until the value at the updated left boundary is less than or equal to ϵ. By the same token, it checks the value at the right boundary () and if the value is greater than ϵ, then it expands the right boundary to the right until the value at the updated right boundary is less than or equal to ϵ. Finally, it computes the values of the SAF likelihood only within the left and right boundaries and outside of which we set the values of the SAF likelihood to zero—i.e. is computed by Equation (5) if 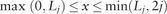 and otherwise . By doing this at each step of calculating the SAF likelihood, it only computes number of elements, which is dynamically changing at each updating step, but always much smaller than . We present the pseudo-code for the score-limited DP algorithm in the Supplementary Appendix.
and otherwise . By doing this at each step of calculating the SAF likelihood, it only computes number of elements, which is dynamically changing at each updating step, but always much smaller than . We present the pseudo-code for the score-limited DP algorithm in the Supplementary Appendix.
This revised algorithm has connections with existing score-limited DP algorithms. For example, in a score-limited Smith–Waterman algorithm, the DP matrix is explored in both directions starting from the mid-point of the hit. When the alignment score drops off by more than ϵ (a user-defined parameter), the extension is truncated. Our adaptive algorithm is similar to this algorithm in that it uses ϵ to stop computing values of the updated SAF likelihood. We found in practice that our choice of ϵ () behaves well, but users are encouraged to test the algorithm and decide the appropriate value for themselves (ϵ is a command-line parameter of our software). Our algorithm is, however, different in that it does not extend from the mid-point in both directions, but it proposed the left and right boundaries and computation is done from right to left. This is required because in real implementation, the updated SAF likelihood for j individuals stored in the same vector for the SAF likelihood for j – 1 individuals and in order to properly update values, computation should be done from right to left.
Figure 3 shows with an example how that the score-limited DP algorithm captures the important regions of the SAF likelihood. Hence, the score-limited DP algorithm is faster than the original DP algorithm, as reflected by the reduced computation area (shown in gray in Fig. 3). Moreover, we retain the accuracy of the final SAF likelihood with the score-limited DP algorithm and it is as stable as the rescaled DP algorithm. The shape of the distribution is identical in all four cases (original, rescaled, banded and score-limited), reflected by the same mean and variance of in all four cases (Fig. 3).
3 Methods
3.1 Generating simulated sequences
To compare the four algorithms (original, rescaled, banded and score-limited DP algorithm) for computing SAF likelihoods, we generated aligned short-read sequencing data by changing sequencing coverage (3×, 5× and 10×) and sample size (50, 100, 300, 500 and 1000 diploid individuals). For this purpose, we first conducted population genetic simulations to produce haplotype data of a given sample size assuming the standard model (with an effective population size of 10 000 diploid individuals, a mutation rate per-base per-generation of and a recombination rate of ), and then overlaid sequencing errors (with error rate of 0.001) to generate paired-end short-read sequencing data given sequencing coverage. For detailed descriptions of the coalescent and sequencing simulations, refer Material and Methods section in Han et al. (2014).
3.2 Sequencing data from the 1000 Genomes Project
To demonstrate the score-limited DP algorithm’s utility with real data, we downloaded the VCF file and the BAM files from the 1000 Genomes Project FTP site in order to estimate the SFS. We used the genotype calls of 365 European and 228 sub-Saharan African individuals from the VCF file, which contains the genotype calls for 1092 individuals sampled from 14 populations drawn from Europe, East Asia, sub-Saharan Africa and the Americas (1000 Genomes Project Consortium, 2010, 2012). For the BAM files, we only used low-coverage Illumina sequencing data (coverage 2× to 4×) (1000 Genomes Project Consortium, 2010, 2012) for these same individuals. Due to file size constraints, we downloaded only a subsection of the genome (region of 10–20 Mb in chromosome 10) by using SAMtools (version 0.1.18) (Li et al., 2009).
3.3 Estimating the SFS
To infer the SFS from simulated aligned short-read sequencing data, we used the direct estimation approach using the freely available program ANGSD (version 0.588) with the EM algorithm option to obtain the MLE of the SFS (Nelson et al., 2012). We refer to results of this procedure as Original. Then, we modified the source code of ANGSD to implement the rescaled DP and the score-limited DP algorithm. All code is written in C++.
For the 1000 Genomes Project data, we evaluated two approaches to infer the SFS: the call-based and direct estimation approaches. For the call-based estimation approach, we used genotype calls in the VCF file and then reconstructed the SFS by allele counting using vcfTools (version 0.1.10) (Danecek et al., 2011). For the direct estimation approach, we directly estimated the SFS from the BAM files with the score-limited DP algorithm.
To evaluate the accuracy of the SFS estimated from simulated short-read sequencing data, we computed the relative deviation of the inferred SFS (computed from sequencing data) compared with the ground-truth SFS (computed from the known values for the genotype data) in each derived allele frequency bin :
where represents a fraction of sites with a derived allele frequency in the inferred SFS and represents a fraction of sites with a derived allele frequency in the ground-truth SFS.
4 Results
We evaluated whether the score-limited DP algorithm is robust to different sequencing coverage and the variance in the site likelihood vector. This evaluation is important because one of the characteristics of the next-generation sequencing data is highly variable coverage across sites that affect the variance of the genotype likelihood vector at the individual-level and the variance of the site likelihood vector at the sample-level.
4.1 Performance for changing sequencing coverage
First, we investigated the impact of different sequencing coverage on the performance of the score-limited DP algorithm in computing the SAF likelihood. For this purpose, we simulated sequencing data for 50 diploid individuals under the standard model at coverage 3×, 5× and 10×. Figure 4A shows how the SAF likelihood is updated at a random site with true allele frequency of 0.51 as a function of sequencing coverage. We observed that the SAF likelihood is more diffuse as coverage decreases, whereas it is more peaked around the true allele frequency of 0.51 as coverage increases (Fig. 4A, the variance of the SAF likelihood is 7.2 with 3×, 2.3 with 5× and 0.21 with 10×). This is because the genotype likelihood vectors tend to be more spread out at low coverage, whereas they tend to be more peaked at the unknown individual genotype at high coverage. This implies that if the banded DP algorithm is used, the choice of bandwidth should depend on coverage—the higher coverage, the smaller d. With this simulated data, we used d of 15 for 3×, 10 for 5× and 5 for 10×, and this worked well for all sites (Fig. 4A, Banded). However, this requires for users to calibrate an appropriate bandwidth before using the algorithm. This difficulty of choosing the appropriate bandwidth is solved with the score-limited DP algorithm. We observed that the optimal bandwidth is adaptively chosen at each updating step (each row of the lower triangular matrix) with the score-limited DP algorithm, and this resulted in a more tight computation area to approximate the SAF likelihood compared with that with the banded DP algorithm. Furthermore, the resulting SAF likelihood has a comparable accuracy to the SAF likelihood computed by the rescaled DP algorithm across all coverage (Fig. 4A). The shape of the distribution is the same, with the same mean and standard deviation of for all three algorithms across coverage.
4.2 Performance for variation in the site likelihood vector
Next, we evaluated that whether the score-limited DP algorithm works well with real data. For this purpose, we used low-coverage sequencing data for 50 diploid GBR individuals in the 1000 Genome Project, and then compared the SAF likelihood computed by the three algorithms (rescaled, banded and score-limited) at multiple random sites with the same best-guess allele frequency in the sample. Compared with the simulated sequencing data matched at average coverage (5×), we observed that low-coverage sequencing data in the 1000 Genomes Project tend to have bigger site-to-site variation of the SAF likelihood. Figure 4B shows how the SAF likelihood is updated at two random sites with the best-guess allele frequency of 0.5 in the sample. We observed that the first site (position 10 012 499 in chromosome 10) has a bigger variance in the SAF likelihood than the second site (position 10 085 321 in chromosome 10)—the variance of the SAF likelihood at the first site is 12, whereas that at the second site is 1.4 (Fig. 4B). Due to large differences in the variability of the SAF likelihoods, the banded DP algorithm with the uniform bandwidth (d = 10) performs badly for the first site but performs well for the second site. However, unlike the banded DP algorithm, the score-limited DP algorithm performs well for both sites, because it is capable of changing the bandwidth accordingly to the observed variance of the SAF likelihood at different sites—the larger the variance of the SAF likelihood, the larger the bandwidth. Moreover, the resulting SAF likelihood computed by the score-limited DP algorithm has a comparable accuracy to that computed by the rescaled DP algorithm—same shape, and the mean and standard deviation with the three algorithms (Fig. 4B)
4.3 Evaluating the accuracy of the inferred SFS
We evaluate the accuracy of the inferred SFS by the score-limited DP algorithm (score-limited) compared with the inferred SFS using the original DP (original). For this comparison, we simulated 100 replicates of sequencing data for 100, 300 and 500 diploid individuals each from genomic regions of length 100 Kb under the standard model. The accuracy of the inferred SFS was evaluated by two metrics: (i) the shape of the inferred SFS in comparison to the ground-truth SFS (Fig. 5A) and (ii) the relative deviation of the inferred SFS compared with the ground-truth SFS at each allele frequency bin (Fig. 5B).
Fig. 5.
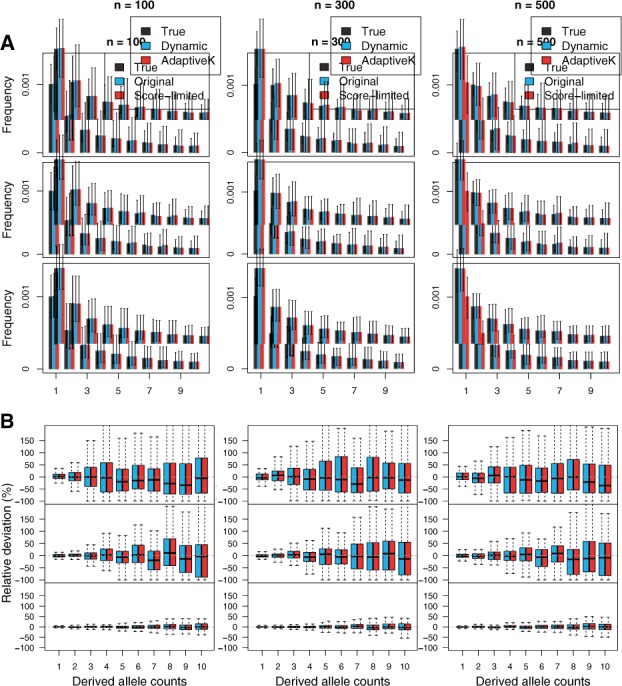
The accuracy of the inferred SFS as a function of sequencing coverage for different sample sizes. The sequencing data were simulated at coverage 3× (top), 5× (middle) and 10× (bottom) with the error rate of 0.001 and the sample size of 100, 300 and 500. (A) Shapes of the inferred SFS (shown in colors in legend) compared with the ground-truth SFS (shown in gray). (B) Relative deviation of a fraction of sites with the derived allele counts of 1–10
We found that the score-limited DP algorithm behaves equivalently to the original DP algorithm. We observed the identical shape of the inferred SFS (Fig. 5) with both algorithms. Moreover, consistent with our previous study (Han et al., 2014), both algorithms led to unbiased estimates of the SFS even at low coverage (such as 3×) regardless of sample size. The shape of the inferred SFS was similar to the ground-truth SFS (Fig. 5A) and the relative deviation of the inferred SFS was close to 0 in all allele frequency bins (Fig. 5B) across all sequencing coverage.
4.4 Runtime comparisons
We next evaluated the runtime for computing site likelihood vectors by the score-limited DP algorithm (score-limited) compared with the runtime by the original DP algorithm (original). We observed runtime speed-ups with the score-limited DP algorithm compared with the original DP algorithm for all sample sizes we tested (Fig. 1). For example, on average, with 500 individuals we observed 5.3-fold speed-up, and with 1000 individuals we observed 8.4-fold speed up. Moreover, consistent with our expectation, the runtime of the original DP algorithm increases quadratically with sample size, whereas the runtime of the score-limited DP algorithm has a linear fit (Fig. 1). These results imply that as a sample size increases, we will observe even more dramatic differences in the runtimes of the two algorithms. For example, when we extrapolated runtime from the results with , we expect 17.5-fold speed-up with 2500 individuals and 63-fold speed-up with 10 000 individuals. The speed improvement with the score-limited DP algorithm will greatly facilitate direct inference of the SFS even when the number of individuals is large.
We want to emphasize that the runtime in Figure 1 is per 10 Mb region, and for the whole genome the runtime would be greater by a factor of 300. However, computational efficiency can be further improved by distributing SAF likelihood computation across nodes. Another possibility is sub-sampling random sites across the genome and distributing the SAF likelihood computation across nodes based on only those sub-sampled sites.
We also note that the score-limited DP algorithm will have less memory usage than the original DP algorithm, which requires memory on the order of n to store the SAF likelihood. With the score-limited DP algorithm, the memory needed is to store the elements of the vector, and we expect that number to stay nearly constant or to scale upwards slowly in proportion to n. In our implementation, when writing the output of the SAF likelihood to a file, at each site, we only output non-zero values of the SAF likelihood, the left boundary (Ln), and the number of non-zero values (), rather than outputting all values. This vastly saves file size to store SAF likelihoods across all sites, and requires less memory to read in the SAF likelihood file to subsequently run an EM algorithm or a BFGS algorithm. For example, for simulated sequencing data of 500 individuals at 5×, the size of the SAF likelihood file is 764 Mb with the original DP algorithm, whereas that with the score-limited DP algorithm is 8.9 Mb. For simulated sequencing data of 1000 individuals at 5×, the file size with the original DP algorithm becomes 1.5 Gb, whereas that with the score-limited algorithm is 9.0 Mb.
4.5 Application to the low-coverage 1000 Genomes Project sequencing data
Finally, we compared the SFS inferred by the call-based approach with the SFS inferred by the direct estimation approach using our score-limited DP algorithm. We used 365 European (EUR) individuals and 228 sub-Saharan African (AFR) individuals to infer the SFS. For the call-based estimation approach, we used the genotype calls stored in the VCF file and then estimated the SFS by allele counting. Note that the VCF file is generated by an LD-aware multisample genotype calling pipeline (1000 Genomes Project Consortium, 2012). For the direct estimation approach, we inferred the SFS directly from low coverage short-read sequencing data (stored in the BAM files, coverage 2×–4×) using our score-limited DP algorithm.
First, we constructed the SFS for 365 EUR individuals with either the call-based approach or the direct estimation method. We observed a striking lack of singletons in the call-based SFS compared with the directly estimated SFS (Fig. 6A and B). The proportion of singletons in the inferred SFS by the VCF file is 0.21 and that by the BAM files is 0.38 (Fig. 6A), showing that 82% less singletons are inferred in the 1000 Genomes genotype call sets (Fig. 6B). This is consistent with our previous study (Han et al., 2014) that shows multisample callers lead to underestimation of rare variants, because a small number of correct alternate reads tend to be ignored. Consistent with this, we observed more positive Tajima’s D for the call-based SFS compared with the directly estimated SFS (Fig. 6C). Moreover, we observed an excess of sites fixed for an ancestral allele in the called-based SFS, implying that there might be more polymorphic sites in the genetic region we analysed than the reported polymorphic sites in the VCF file provided from the 1000 Genome Project (data not shown).
Fig. 6.
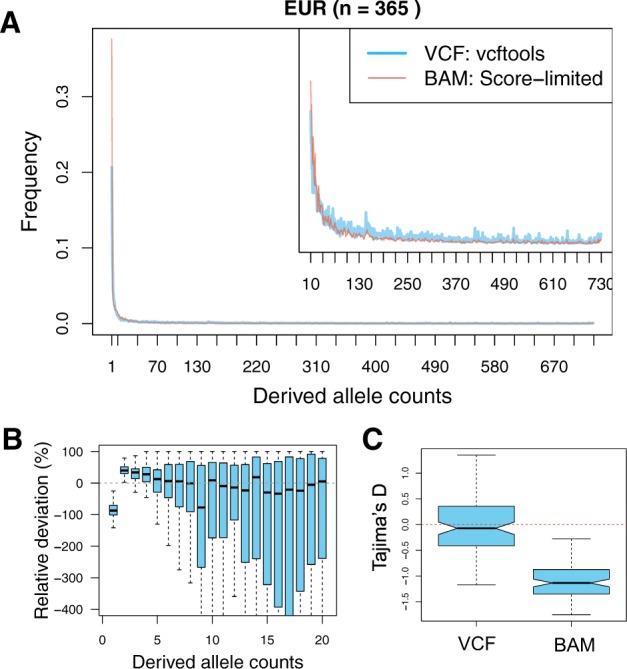
Comparison of the called-based SFS (referred to as VCF: vcftools) and the directly estimated SFS (referred to as BAM: Score-limited). The SFS was constructed for 365 EUR individuals in the 1000 Genomes Project. (A) Shapes of the inferred SFS (shown in colors in legend). As the VCF file only contains sites that are inferred to be polymorphic, we only considered polymorphic sites for the SFS inferred from the BAM files and rescaled it so that all elements sum to 1. (B) Relative deviation of a fraction of sites with the derived allele count of 1–20. We computed the relative deviation of the SFS inferred from the BAM files compared with the SFS computed from the VCF file in each derived allele frequency bin . (C) Tajima’s D comparison
Next, we inferred the SFS for 228 AFR individuals and a combined sample of 593 EUR and AFR individuals with either the call-based approach or the direct estimation approach. We observed a similar pattern as with the European population, implying that our results apply to all samples in the 1000 Genomes Project (data not shown).
5 Discussion
A large sample size enables us to infer more precise summary statistics and parameters in many population genetic analyses. However, at the same time, we confront computational challenges with large samples and in many cases, we have to deal with these challenges to make the method practical with large sample sizes. We showed that although the direct estimation approach for computing the SFS can provide the unbiased SFS even at low coverage, it does not scale up to large sample sizes because the computation time for running this method is quadratic in a number of diploid individuals. To overcome this problem, we developed a new algorithm, called the score-limited DP algorithm, and showed that the computation time for running this algorithm is linear in the number of genomes. This algorithm exploits the observation that for most sites the SAF likelihood’s non-negligible values are all concentrated on a few elements around the element corresponding to the best-guess allele count. Therefore, we approximate this vector by curtailing computation to only a few components of the DP update vectors. More importantly, this algorithm can adaptively choose the bandwidth d during updating the SAF likelihood for each site. We showed that the bandwidth change is robust to sequencing coverage and the variation of the SAF likelihood. We also showed that the EM combined this new algorithm has comparable accuracy but is 8-fold faster than the original DP combined with the EM algorithm when analysing the data from 1000 individuals. Our new algorithm’s improvement in speed makes it possible to directly estimate the SFS from very large samples of low coverage short-read sequencing data.
Our score-limited DP algorithm could be applied to other DP algorithm whose runtime is quadratic in a sample size. For example, Yi et al. (2010) proposed an empirical Bayes approach to estimate a posterior probability of a minor allele frequency (MAF). They used a DP algorithm to effectively compute summation over all possible genotype configurations for n diploid individuals, and therefore this algorithm has a runtime complexity of similar to the DP algorithm introduced here. Furthermore, similar to the distribution of the SAF likelihood, the distribution of the posterior probabilities of the MAF is unimodal and most of the probabilities are close to 0. Therefore, we can apply our score-limited DP algorithm for this DP algorithm to reduce runtime complexitiy to be O(dn) rather than original where d is the maximum bandwidth.
Our score-limited DP algorithm can also be directly applied to speed up estimation of the 2D SFS. Li (2011) derived the EM algorithm to get the MLE of the 2D SFS as an extension to the 1D SFS estimation, and this requires precomputation of the SAF likelihoods for all sites for each population independently. This implies that we can make this method faster with the score-limited DP algorithm compared with the original DP algorithm. The computation time for running the original algorithm is , whereas the runtime of the score-limited DP algorithm becomes , where n1, n2 represent a sample size for each population and d1, d2 are the maximum bandwidth.
One might argue that uncertainty associated with genotype calls can be overcome by simply increasing sequencing coverage and there is therefore little need for algorithms that handle low coverage data. However, cost constraints require difficult choices between increasing sample size and increasing coverage. There are certain cases where one prefers a large sample of low-coverage sequencing data over a smaller sample size with high coverage. For example, in genome-wide association studies, one can obtain more power by sequencing a large number of individuals at low coverage (Kim et al., 2010; Pasaniuc et al., 2012). As another example, identification of rare variants always requires large sample sizes, and moderately rare loci will be detectable even with low coverage data. Finally, even though sequencing cost keeps dropping, cost constraints will not disappear because users will continue to work with limited budgets and push these limits with applications involving very large numbers of individuals; thus we expect low-coverage sequencing will remain an attractive approach for many investigators and that methods like ours will retain their appeal for the foreseeable future.
Supplementary Material
Acknowledgement
We thank Darren Kessner for his assistance with the sequencing simulations.
Funding
This study was funded by National Institutes of Health [T32 HG002536 to E.H., GM053275 to J.S. and HG007089 to J.N.].
Conflict of interest: none declared.
References
- 1000 Genomes Project Consortium (2010) A map of human genome variation from population-scale sequencing. Nature , 467, 1061–1073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 1000 Genomes Project Consortium (2012) An integrated map of genetic variation from 1,092 human genomes. Nature , 491, 56–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Achaz G. (2008) Testing for neutrality in samples with sequencing errors. Genetics , 179, 1409–1424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Achaz G. (2009) Frequency spectrum neutrality tests: one for all and all for one. Genetics , 183, 249–258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andolfatto P. (2007) Hitchhiking effects of recurrent beneficial amino acid substitutions in the Drosophila melanogaster genome. Genome Res., 17, 1755–1762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Begun D.J., et al. (2007) Population genomics: whole-genome analysis of polymorphism and divergence in Drosophila simulans. PLoS Biol., 5, e310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danecek P., et al. (2011) The variant call format and VCFtools. Bioinformatics , 27, 2156–2158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DePristo M.A., et al. (2011) A framework for variation discovery and genotyping using next-generation DNA sequencing data. Nat. Genet., 43, 491–498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Excoffier L., et al. (2013). Robust demographic inference from genomic and SNP data. PLoS Genet., 9, e1003905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fay J.C., Wu C.I. (2000) Hitchhiking under positive Darwinian selection. Genetics , 155, 1405–1413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu Y.X., Li W.H. (1993) Statistical tests of neutrality of mutations. Genetics , 133, 693–709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu W., et al. (2013) Analysis of 6,515 exomes reveals the recent origin of most human protein-coding variants. Nature , 493, 216–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutenkunst R.N., et al. (2009) Inferring the joint demographic history of multiple populations from multidimensional SNP frequency data. PLoS Genet., 5, e1000695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han E., et al. (2014) Characterizing bias in population genetic inferences from low-coverage sequencing data. Mol. Biol. Evol., 31, 723–735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S.Y., et al. (2010) Design of association studies with pooled or un-pooled next-generation sequencing data. Genet. Epidemiol., 34, 479–491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H. (2011) A statistical framework for SNP calling, mutation discovery, association mapping and population genetical parameter estimation from sequencing data. Bioinformatics , 27, 2987–2993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H., et al. (2009) The sequence alignment/map format and SAMtools. Bioinformatics , 25, 2078–2079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson M.R., et al. (2012) An abundance of rare functional variants in 202 drug target genes sequenced in 14,002 people. Science , 337, 100–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen R., et al. (2012) SNP calling, genotype calling, and sample allele frequency estimation from New-Generation Sequencing data. PLoS ONE , 7, e37558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pasaniuc B., et al. (2012) Extremely low-coverage sequencing and imputation increases power for genome-wide association studies. Nat. Genet., 44, 631–635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sung W.-K. (2009) Algorithms in Bioinformatics: A Practical Introduction (Chapman & Hall/CRC Mathematical & Computational Biology), 1st edn Chapman and Hall, London, UK. [Google Scholar]
- Tajima F. (1989) Statistical method for testing the neutral mutation hypothesis by DNA polymorphism. Genetics , 123, 585–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi X., et al. (2010) Sequencing of 50 human exomes reveals adaptation to high altitude. Science , 329, 75–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


