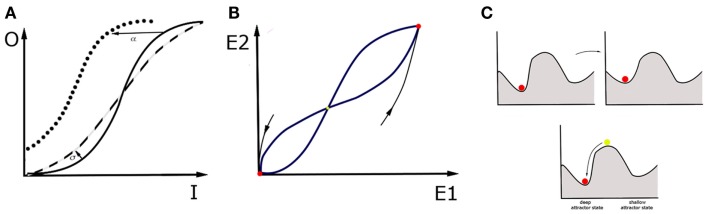
Figure 2.
Wilson–Cowan model and a “ball” metaphor. The activity of a single brain area within the network is a consequence of the synaptic inputs from other areas, the modulatory tone generated by diffuse projections, and the recurrent connectivity within the brain area itself. The activity reflects a specific balance between excitation and inhibition within the area. For simplicity, we describe the activity by one variable, E, for which the following equation holds: . The first term on the right tells us that in the absence of any drive (provided by the second term), the activity decays to zero with time scale τ. The second term incorporates the contribution of recurrent connectivity via E itself, input from other areas, represented by I, and the level of neuromodulation, represented by M. Each of these contributions are weighted by factors: α, β, and γ respectively. When the second term is positive, it increases the level of activity. The function f is a response function that translates the sum of activities into a driving term, and is typically sigmoidal (106): . In this form, A is the maximum that f can reach for large x values, and σ is the value for which f is equal to half its maximum value. In addition, it also specifies how steeply f increases with x, a quantity that is also referred to as the gain factor. Note that this expression only holds for positive x values, f is zero when x is negative. This model has a range of parameters, which is important because each of them can be linked to specific physiological processes and changes in circuit structure. For instance, an increased β represents a stronger synaptic projection, whereas an increased α represents stronger recurrent synapses. An increased M reflects the effect of neuromodulators that increase the level of depolarization in the cells, and hence the baseline firing rate; γ reflects the sensitivity to neuromodulators of cells and circuits. The value of σ can be interpreted as a change in gain. (A) In a given region, the sigmoidal input-output (I-O) relationship has three regimes. For small input it increases rapidly. For large inputs, it saturates. For values in between, it connects these regimes linearly. If the σ value, and thus excitability of the region, grows (dashed line), the I-O function is steeper than in the control case (solid line). If the region gets stronger recurrent connectivity, input from other regions or neuromodulation, so that the α, β, γ values grow respectively, I-O function shifts to the left (dotted line). (B) In an example of two interconnected regions, E1 and E2, this dynamical system has three fixed points that are candidates for attractor states. In this example, two of them are stable (red). For a given attractor, setting activities E1, E2 to arbitrary initial values within the basin of attraction will make the system move on toward this attractor. The third fixed point is unstable (yellow), which means that every small perturbation from this state makes the system fall into one of the basins of attraction, and thus end up in one of two attractor states. (C) One may picture attractor states with the ball metaphor. Disease can be represented in two ways. It can mean a change in the landscape of basins of attraction: some attractor states change position and even if the patient occupies the original attractor throughout the process, their brain state gradually changes the attractor state that they occupy. This can be achieved by changing shape of I-O function with use of parameters σ and α, β, γ or changing of relaxation time constants τ. However, it can also mean that, in a result of intrinsic noise in the brain or in response to a particular external input, the brain state in the patient is triggered to switch to another “wrong” basin of attraction. The noisy behavior of the network is not captured by the basic version of Wilson–Cowan equations, but incorporating noise in and therefore also a stochastic driving force is also possible. An attractor is a network state where the levels of activity do not change anymore, hence E is constant. Mathematically, this means that E does not change over time, hence that its value is given by setting the right hand side of equation (1) to zero, which yields hence f gives the steady state values, hence increases in the factors α, β, and γ immediately increase the E value. It is important to realize that this is an equation from which E needs to be found. In the preceding, we focused on a single variable E, but in a network there is at least one variable for each brain area involved. For multiple brain regions involved, which is true in MDD, . Here i represents the index of the brain area and j is the index of brain areas that provide input. Most parameters now have an index i, because their value depends on the area they represent. We have also included a stimulation current, which represents the effects of electric or magnetic stimulation. Within this framework, the effects of treatments can be captured. On one hand, treatments can reshape the attractor landscape. For instance, pharmacological manipulations can either change the level of neuromodulation or the sensitivity of the circuit to neuromodulators. This would lead to the homeostatic regulation of the coupling coefficients Jij, and σ, and, subsequently, to the change in the map of attractors. On the other hand, a single electrical stimulation, such as ECT session, could change the attractor, offering temporary relief; but if the new attractor is not stable, the brain network could return to the old attractor over time. A sequence of electrical stimulation would also affect Jij and thus change which attractors are possible and how stable they are. Taken together, electrical stimulation has the advantage that its effect is local and can be tuned to alter/correct a specific Jij value.