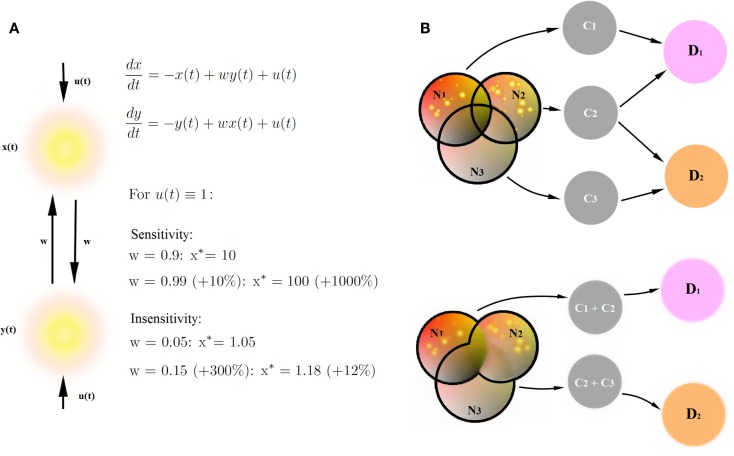
Figure 4.

Benefits of CCM. (A) Stable connectivity patterns and connectivity strengths are two sides of the same coin. Let us assume that our sigmoidal transfer function can be approximated as a simple linear function. We provide an example of a network sensitive to changes in connectivity strengths (a small change in connection weights yields an huge change in the value of stable activation patterns) and an example of a network insensitive to changes in connectivity strengths (a huge change in the connectivity strengths yields a small change in stable activation patterns). Therefore, the description of networks by means of dynamical systems provides more versatile description than connectivity strengths in the networks or stable connectivity patterns alone. (B) Decomposition of psychiatric disorders into a number of diagnostic traits helps causal inference in the diagnostic process. Networks N_i underlie cognitive constructs C_i diagnostic to psychiatric disorders D_i. Disorders D₁ and D₂ share a common cognitive construct C₂, but involve also disorder-specific diagnostic constructs C₁ and C₃. Let us assume that the joint posterior distribution for every disorder D_i factorizes into posterior probability distributions for single diagnostic constructs. Let us further assume that we find the same, specific pathologies in networks N₁ and N₂. If we can decompose the D₁-related network into a sum of networks N₁ and N₂ underlying single diagnostic constructs C₁ and C₂ (upper panel), we collect more evidence for the disorder D₁ (pathologies in both networks linked to diagnostic constructs) than for the disorder D₂ (pathology in one out of two networks linked to diagnostic constructs). On the other hand, if we are not able to decompose D₁ and D₂-related networks into networks underlying single diagnostic categories (lower panel), the amount for evidence in favor of both disorders is the same because both networks (N₁ + N₂) underlying disorder D₁ and (N₂ + N₃) underlying disorder D₂ are pathological.