Correlating Structural and Energetic Changes in Glycine Receptor Activation

Background: Interactions between Gln^−26′ (in M1 domain), Arg^19′ (in M2 domain), and Lys^24′ (in M2-M3 linker) may reveal molecular mechanisms of glycine receptor activation.

Results: α1^Q−26′E-containing receptors have longer active periods and lower conductances.

Conclusion: The energy for activation is distributed broadly at the transduction zone.

Significance: These energetic interactions are likely present in multiple pentameric ligand-gated ion channels.

Abstract

Pentameric ligand-gated ion channels (pLGICs) mediate fast chemoelectrical transduction in the nervous system. The mechanism by which the energy of ligand binding leads to current-conducting receptors is poorly understood and may vary among family members. We addressed these questions by correlating the structural and energetic mechanisms by which a naturally occurring M1 domain mutation (α1^Q−26′E) enhances receptor activation in homo- and heteromeric glycine receptors. We systematically altered the charge of spatially clustered residues at positions 19′ and 24′, in the M2 and M2-M3 linker domains, respectively, which are known to be critical to efficient receptor activation, on a background of α1^Q−26′E. Changes in the durations of single receptor activations (clusters) and conductance were used to determine interaction coupling energies, which we correlated with conformational displacements as measured in pLGIC crystal structures. Presence of the α1^Q−26′E enhanced cluster durations and reduced channel conductance in homo- and heteromeric receptors. Strong coupling between α1^−26′ and α1^19′ across the subunit interface suggests an important role in receptor activation. A lack of coupling between α1^−26′ and α1^24′ implies that 24′ mutations disrupt activation via other interactions. A similar lack of energetic coupling between α1^−26′ and reciprocal mutations in the β subunit suggests that this subunit remains relatively static during receptor activation. However, the channel effects of α1^Q−26′E on α1β receptors suggests at least one α1-α1 interface per pentamer. The coupling-energy change between α1^−26′ and α1^19′ correlates with a local structural rearrangement essential for pLGIC activation, implying it comprises a key energetic pathway in activating glycine receptors and other pLGICs.

Introduction

The glycine receptor channel (GlyR)² is an anion-selective member of the pentameric ligand-gated ion-channel (pLGIC) family. pLGICs are comprised of modular domains (Fig. 1A). The ligand binding pockets are found in the extracellular domain, at subunit interfaces, whereas the permeation gate is located at the transmembrane domain (TD). Between the ligand binding pockets and the gate lies a transduction zone (TZ), made of interacting loops that originate from the extracellular domain, such as loops 2 and 7, and the TD, such as the M2-M3 linker (Fig. 1A, inset). Channel activation proceeds as a wave-like progression of structural rearrangements, initiated by the ligand binding reaction (1, 2) and conveyed to the gate via interactions across the TZ (3–5).

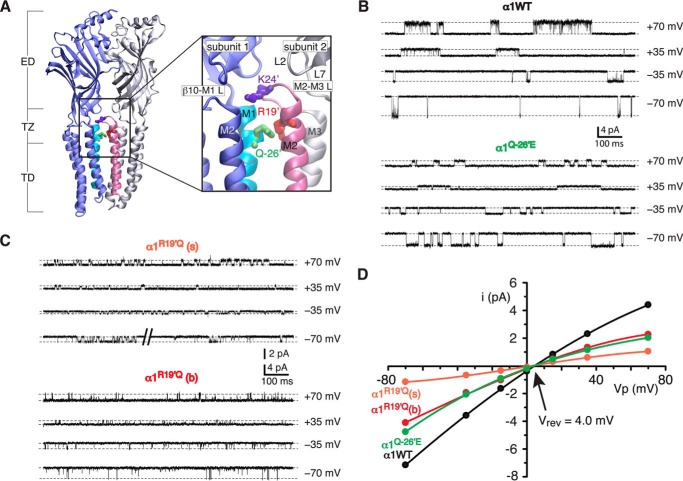
FIGURE 1.

i-V and conductance. A, schematic representation of two adjacent subunits showing the extracellular domain (ED), TZ, and TD. The inset shows an expanded view of the TZ (boxed) and residues Lys^24′ (Lys²⁷⁶), Arg^19′ (Arg²⁷¹), and Gln^−26′ (Gln²²⁶). The schematic is based on the β3 GABA_A receptor (Protein Data Bank code 4COF) (21). B, sample currents obtained at ±70 and ±35 mV for homomeric α1 wild-type and α1^Q−26′E receptors. C, sample currents obtained at ±70 and ±35 mV for the smallest (R19′Q(s)) and largest (R19′Q(b)) current amplitudes of α1^R19′Q homomeric receptors. D, group i-V for the experiments shown in B and C. The number of patches used for the i-V was 10 (wild-type), 11 (Q−26′E), 11 (R19′Q(s)), and 6 (R19′Q(b)).

Structure-function studies of the GlyR, and indeed other pLGICs, have benefitted greatly from the study of naturally occurring mutations that perturb channel activation. These perturbations give rise to impaired neurotransmission at glycinergic synapses, resulting in movement disorders such as hyperekplexia (6). Mutations in the α1 subunit have been most informative in this respect (7). Although this subunit readily forms homomeric receptors, synaptic GlyRs mainly comprise heteromers of α1 and β subunits (8).

Three hyperekplexia-causing point mutations in the α1 subunit TZ are vital for efficient signal transduction. Two of these produce impaired receptor activation; α1^R271Q (α1^R19′Q), which is situated at the extracellular end of M2, and α1^K276E (α1^K24′E) in the M2-M3 linker (Fig. 1A). The α1^R19′Q mutation gives rise to a reduced single channel conductance and a marked decrease in glycine sensitivity when expressed as homomeric receptors (9, 10). Similarly, the α1^K24′E mutation reduces glycine sensitivity in both homo- and heteromeric GlyRs, although no change in single channel conductance was reported (5, 11, 12). A recently identified third mutation, α1^Q226E (α1^Q−26′E), located near the top of M1, gives rise to spontaneous channel opening, a reduction in single channel conductance, but no significant change in whole cell agonist sensitivity (13).

Recently published crystal structures of prokaryotic and eukaryotic pLGIC homologues (14–21) reveal close proximity of residues at 19′, 24′, and −26′. A high degree of sequence conservation is also evident at these positions, especially among anion-selective pLGICs, suggesting a common functional relevance. In particular, the Gln^−26′ side group from one subunit lies in close apposition to Arg^19′ and Lys^24′ in the adjacent subunit (Fig. 1A, inset). Given this proximity, and the observation that all three hyperekplexia-causing mutations involve a potential alteration in charge, it is reasonable to postulate that this discrete TZ subregion constitutes a functional unit with a key role in receptor activation. The recent demonstration, based on whole-cell measurements of α1^Q−26′E homomeric GlyRs, that a glutamic acid occupying position −26′ interacts with the arginine at 19′ during channel activation (22), supports this idea.

With the exception of α1^K24′E-containing receptors, investigations into the effects of mutations at the 19′, 24′, and −26′ positions have mainly been confined to homomeric receptors examined via whole cell patch clamp analysis. This affords only limited mechanistic insights into the channel activation mechanism and, of course, avoids the physiologically relevant α1β GlyR isoform.

To address these deficiencies we conducted a single channel study that examines the effects of charge-altering mutations to 19′, 24′ in the α1 and β subunits, co-expressed on a background of the newly described α1^Q−26′E mutation. We employed two key functional parameters of single channel currents to infer the presence of charge and residue interactions. The first of these was the main unitary conductance state of the channel, which was taken as an index of net charge strength near the central conduction pathway (23, 24). The second parameter was the mean duration that a receptor remains active for (cluster duration) in the presence of agonist. These parameters were used alone or in combination to quantitate the strength of interactions between the 19′, 24′, and −26′ positions in both homomers and heteromers. Our data suggest that receptor activation involves multiple energetic pathways at the TZ.

EXPERIMENTAL PROCEDURES

Cell Culture

HEK AD293 cells were seeded onto poly-d-lysine-coated glass coverslips and transfected with cDNAs encoding human α1 (pCIS) and β (pcDNA 3.1+) GlyR subunits using a calcium phosphate-DNA co-precipitate method. The cDNA encoding the CD4 surface antigen was also added to the transfection mixture and acted as a marker of transfected cells. For some transfections, empty (non-coding) pCIS cDNA plasmid was included to reduce expression levels and facilitate the resolution of single-channel activations (25). To minimize the formation of homomeric receptors, heteromeric GlyRs were expressed by cotransfecting the α1 and β cDNAs at an α1:β ratio of 1:100. We will provisionally assume a stoichiometry and subunit arrangement of β-α1-β-α1-β (26, 27) but will consider other possibilities, see “Discussion.” Cells were used in experiments 2–3 days after transfection. Point mutations were incorporated into the subunits using the QuikChange site-directed mutagenesis method. The homomeric α1^K24′C cross-linking experiments were done on an α1^C41A background. Successful incorporation of mutations was confirmed by sequencing the mutated DNA.

Electrophysiology

All experiments were carried out at room temperature (21–24 °C). Single-channel and macropatch currents were recorded from outside-out excised patches at a clamped potential of −70 mV, unless indicated otherwise. The cells were continuously perfused via a gravity-fed plastic tube with an extracellular bath solution containing (in mm), 140 NaCl, 5 KCl, 1 MgCl₂, 2 CaCl₂, 10 HEPES, and 10 d-glucose and titrated to pH 7.4. Glass electrodes were pulled from borosilicate glass (G150F-3; Warner Instruments), coated with a silicone elastomer (Sylgard-184; Dow Corning), and heat-polished to a final tip resistance of 4–15 MΩ when filled with an intracellular solution containing (in mm) 145 CsCl, 2 MgCl₂, 2 CaCl₂, 10 HEPES, and 5 EGTA, pH 7.4. Excised patches were directly perfused with extracellular solution by placing them in front of one barrel of a double-barreled glass tube. Single channel currents were elicited by exposing the patch continuously to glycine containing solution, flowing through the adjacent barrel, by lateral switching of the tube. Experiments were recorded using an Axopatch 200B amplifier (Molecular Devices), filtered at 5 kHz (2 kHz for the α1^{Q−26′E/R19′A} double mutant) and digitized at 20 (ensemble currents) or 50 kHz (single-channel currents) using Clampex (pClamp 10 suite, Molecular Devices) via a Digidata 1440A digitizer.

Data Analysis

Single-channel current amplitudes were measured in Clampfit. The current amplitude of most receptors was estimated using amplitude histograms. However, for receptors that produced activations containing many unresolved openings (see Fig. 3A) we opted for direct cursor measurement of expanded sections of record that showed fully resolved levels. Multiple measurements of openings of the largest amplitude were made from at least three patches for each channel type held at −70 mV. In current-voltage (i-V) experiments, the amplitude was measured at voltages of ±70, ±35, ±15, and 0 mV. The data were fit to a polynomial function in SigmaPlot (Systat Software) and the reversal potential was read directly off the plots. Single-channel conductance (γ) was calculated from the single-channel amplitude (i) using Ohm's law,

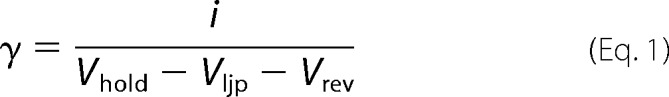where V_hold is the holding potential (−70 mV), V_ljp is the liquid junction potential, and V_rev is the reversal potential. V_ljp was calculated to be 4.7 mV for the solutions used (28). We confined our analysis to the largest, main conductance level.

FIGURE 3.

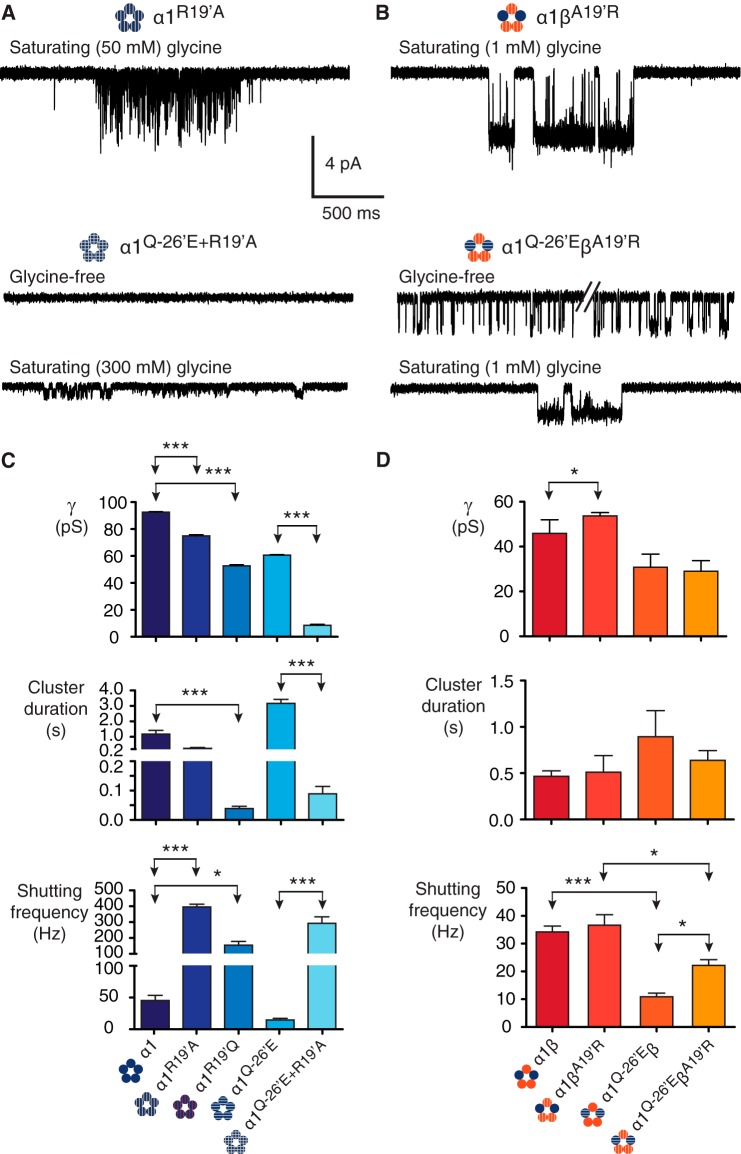
Mutations to 19′. A, homomeric α1^R19′A receptors show evidence of impaired receptor activation. When the α1^R19′A mutation is combined with the α1^Q−26′E mutation in the same subunit (α1^{R19′A/Q−26′E}) and expressed as homomers, the functional impairment was greatest, ablating constitutive activity and markedly reducing conductance. B, heteromeric receptors containing the β^A19′R subunit showed little evidence of functional impairment. When expressed with α1 wild-type (α1β^A19′R) the receptors had similar properties to wild-type α1β heteromers. Similarly, when β^A19′R was co-expressed with α1^Q−26′E the resulting heteromers (α1^Q−26′E-β^A19′R) were little changed compared with the α1^Q−26′E-β heteromers. C, group data summarizing the effects on channel conductance, cluster duration, and intra-cluster shutting frequency for receptors incorporating 19′ mutations. The number of clusters used in the analysis was 284 (α1^R19′A, 4 patches), 378 (α1^R19′Q, 5 patches), 99 (α1^{Q−26′E/R19′A}, 10 patches), 35 (α1β^A19′R, 3 patches), and 133 (α1^Q−26′E-β^A19′R, 5 patches). ***, p < 0.0001; *, p < 0.01.

The QuB suite was used to analyze the kinetic properties of GlyR activations. Segments of single-channel activity separated by long periods of baseline were selected by eye and idealized into noise-free open and shut events using a temporal resolution of 70 μs (29). Idealized data were fit with a simple model in which open and shut states were connected to a central shut state. Rate constants for transitions in the model were optimized using Maximum Likelihood Fitting (30), and states were added, to the central shut state, and re-fit until the log likelihood improved by less than 10 units. This fit was used to determine the critical time (t_crit), which was taken for the shut durations and used to divide the idealized segments into clusters (or bursts at 2 μm glycine). t_crit varied between 9 and 51 ms and generally preserved three shut components when the divided (chopped) data were re-fit in the manner described above. This analysis yielded mean cluster durations, intra-cluster open probabilities (P_o), and number of events per cluster. In addition, we monitored the effects of the mutations on the time constant of the main open exponential component (MOC) in the open dwell histograms of the re-fitted data. The MOC accounted for 51–96% of the current.

We used cluster duration and conductance to assay channel function. Cluster duration is a function of the net affect of all the equilibrium constants in the underlying activation mechanism and, as such, is an integrated index of the entire activation process. A point mutation will affect multiple state transitions along the activation coordinate, and it is experimentally intractable to determine which state-to-state transitions mutations will be affected. Because it is not possible to know, a priori, what the physical correlate of a particular equilibrium constant is, we avoided using any particular equilibrium constant as an index of receptor function, including in the pairwise interaction energy calculations.

Any mutation-induced change in conductance was taken to indicate that a given residue is charged. The magnitude of the change in conductance reflects the strength of the charge. Because we are only interested in factors affecting the activation process, we made no inferences regarding the determinants of permeation to avoid conflating the processes of activation and ion permeation. We used cluster duration and conductance as measures of the electrostatic topography of the gating landscape, exploiting the fact that the region of interest happens to be near the permeation pathway, thus giving us a measurable way of ascertaining the effective charge of relevant residues. As a measure of open state stability we monitored the shutting frequency within active periods. This proved to be a more sensitive stand-alone parameter than more conventional ones, such as intracluster P_o. P_o was only used in conjunction with cluster duration as an alternative method of calculating coupling energies.

Parameter measurements were plotted in Prism 6 (GraphPad). Data were analyzed by ordinary one-way analysis of variance in Prism, and Sidak's multiple comparisons test was used in the case of significance. Because cluster and burst durations, MOCs, and shutting frequencies are exponentially distributed, we analyzed these data on a patch-to-patch basis. Mean values for cluster duration, MOC, and shutting frequency were determined for each patch for a given receptor (these are normally distributed). Analysis of variance tests were applied to these means. The overall mean was then determined for plotting and data interpretation. Statistical significance was set at p < 0.01, and all data are presented as mean ± S.E.

Cluster (or burst) durations were determined for the largest conductance level for each receptor. The energy of interaction between two residue positions incorporating mutations in the receptors was determined using,

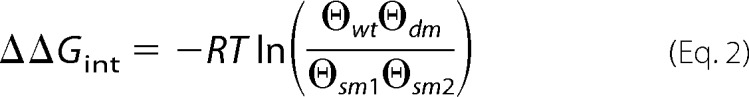where ΔΔG_int is the first-order coupling free energy (in kJ mol⁻¹) in a mutant cycle, R is the gas constant, T is absolute temperature, and ϴ is the product of the channel conductance and cluster duration at saturating concentrations of glycine for wild-type (wt), double mutant (dm), single mutant 1 (sm1), and single mutant 2 (sm2). Alternative parameters for ϴ are shown in Table 2.

TABLE 2.

Pairwise coupling energies between α1^Q−26′E and 19′ or 24′ positions in α1 and β subunits

	ϴ parametera	α1Q−26′E-α1R19′A	α1Q−26′E-α1K24′A	α1Q−26′E-βA19′R	α1Q−26′E-βK24′A
Pairwise coupling energy (kJ mol−1)	Clust. × Cond.	9.43	−0.97	1.60	−0.32
	Clust.	5.09	−1.06	1.06	−0.54
	Cond.	4.34	0.09	0.54	0.22
	Clust. × Po	7.36	−3.84	1.09	−0.46
	MOC	4.68	−3.29	−1.08	1.17

^a Clust., mean cluster duration (ms); Cond., conductance (pS); P_o, intracluster open state occupancy.

Ensemble currents were recorded in response to brief (<1 ms) exposure to a saturating concentration of glycine by rapidly moving the double-barreled tube by means of a piezoelectric translator (Siskyou MXPZT-300), controlled by a voltage-step protocol in Clampex. The exchange time (rise and decay ∼200 μs) was verified for each recording session by monitoring changes in the liquid junction potential using an open-tip electrode. Ten to fifteen responses from each patch were peak-normalized and averaged. The rise and decay times constants were measured by fitting 10–100% of the rising phase of the current to,

and the 20–80% of the decay phase of the current using,

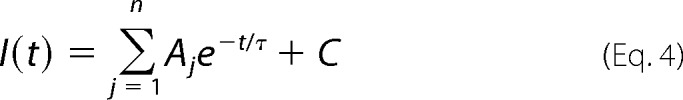where A is the amplitude, t is time, τ is the time constant, and C is a constant. The number of components (j) ranged from one to three to give the best fit as determined by eye. To facilitate comparison between the decay time constants, the weighted average time constant (τ_w) was calculated using the following equation.

RESULTS

Current-Voltage (i-V) Plots and Conductance

Our first experiments were aimed at accurately calculating the conductance of each receptor at −70 mV. Single channel current amplitude was measured over a voltage range of ±70 mV for three GlyRs to establish if the reversal potential varied between receptors incorporating a change of charge near the extracellular pore entrance. We tested the homomeric α1 wild-type, α1^Q−26′E, and α1^R19′Q receptors, the latter two involving a potential alteration in charge near the pore lumen. The largest, predominant current level was considered for α1 wild-type and α1^Q−26′E receptors, elicited by glycine concentrations of 20 μm (α1 wild-type) and 1 μm (α1^Q−26′E) (Fig. 1B, Table 1). Previous reports suggest that the homomeric α1^R19′Q GlyR exhibits either a single conductance of 18 pS (10) or two conductances, with one being predominant (15 pS, >99%) and the other being rare (37 pS, <1%) (9). We found that α1^R19′Q receptors exhibited multiple levels when exposed to glycine concentrations from 2 to 300 mm. We analyzed the smallest and largest of these levels (Fig. 1C). The i-V for all three channels intersected the voltage axis at 4.0 mV (Fig. 1D), allowing us to correct for the driving force according to Equation 1. The corresponding conductance calculations yielded values of 92.5 ± 0.3 pS for α1 wild-type and 60.6 ± 0.4 pS for α1^Q−26′E receptors. For the α1^R19′Q receptors the conductance values were 14.9 ± 0.5 and 52.7 ± 0.8 pS for the small and large amplitude currents, respectively. As all four plots reversed current at 4.0 mV, irrespective of the receptor type or conductance level measured, we infer that mutations at the subregion under investigation do not affect the reversal potential. For calculations of conductance for other receptors we will assume that they too reverse current at 4.0 mV.

TABLE 1.

GlyRs used in this study

	α1 Homomers	α1β Heteromers
Wild-type	α1	α1β
Mutants	α1Q−26′E	α1Q−26′Eβ
	α1R19′Q
	α1R19′A	α1βA19′R
	α1K24′C
	α1K24′A	α1βK24′A
	α1Q−26′E/R19′A	α1Q−26′E-βA19′R
	α1Q−26′E/K24′A	α1Q−26′E-βK24′A

Wild-type and α1^Q−26′E Homo- and Heteromeric GlyRs

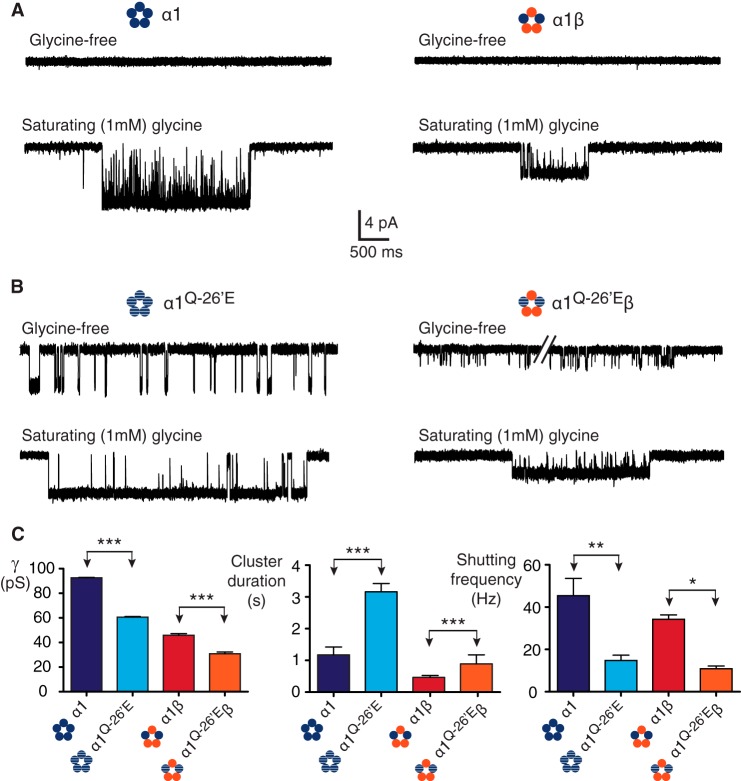
Having established an accurate method for calculating channel conductance, we compared single channel currents recorded from homomeric α1 wild-type and α1^Q−26′E receptors, with those of the same receptors incorporating the β subunit (Table 1). As previously noted, wild-type homo- and heteromeric receptors exhibit negligible spontaneous (agonist-free) activations (12, 31)(Fig. 2A, above). At a saturating (1 mm) glycine concentration, active periods occurred as clusters of openings flanked by quiet periods that correspond to receptor desensitization (Fig. 2A, below). We also observed spontaneous channel activity in α1^Q−26′E homomeric receptors (Fig. 2B above), as previously reported (13). As evidence was adduced for an interaction between the introduced glutamic acid at −26′ in one subunit and the Arg¹⁹′ position in the adjacent subunit (22) we investigated the effect of introducing the wild-type β subunit, which has an alanine at 19′. To our surprise, α1^Q−26′E-β heteromers were also constitutively active (Fig. 2B, above). This suggests that there might be additional residues that can interact with α1^Q−26′E in α1 and β subunits that give rise to spontaneous openings, or that at least one α1-α1 interface exists in α1β heteromeric receptors.

FIGURE 2.

Constitutive activity in α1^Q−26′E-containing homo- and heteromeric GlyRs. A, wild-type α1 homo- and α1β heteromeric receptors show no significant spontaneous activity in glycine-free solution. In saturating glycine receptor activations occur as clusters of open and shut events that define the activity of a single channel. In this and all subsequent figures, recordings were performed at −70 mV and channel openings are downward deflections. B, in the absence of glycine, α1^Q−26′E homo- and α1^Q−26′E-β heteromeric receptors activate in brief bursts. In saturating glycine, α1^Q−26′E-containing receptors activate in clusters of longer duration, lower conductance, and a reduced intra-cluster shutting frequency compared with their wild-type counterparts. C, group data summarizing the effects on channel conductance, cluster duration, and intra-cluster shutting frequency for wild-type and α1^Q−26′E-containing receptors. The number of clusters used in the analysis was 175 (α1 wild-type, 10 patches), 69 (α1β wild-type, 8 patches), 124 (α1^Q−26′E, 9 patches), and 72 (α1^Q−26′E-β, 9 patches). ***, p < 0.0001; **, p < 0.001; *, p < 0.01.

Channel conductance, cluster durations, the MOC, and the shutting frequency within each cluster were determined for the four receptors (Fig. 2C). Consistent with previous reports (12, 32, 33), the main conductance for wild-type homo- and heteromeric receptors was 92.5 ± 0.3 and 45.9 ± 1.4 pS, respectively. The mean cluster duration for wild-type α1 receptors was 1175 ± 246 ms and for α1β receptors was 466 ± 60 ms. The shutting frequency within clusters, a measure of open state stability, for α1 and α1β wild-type receptors was 45 ± 8 and 34 ± 2 Hz, respectively. The corresponding MOCs for α1 and α1β receptors were 24 ± 6 (fraction 74 ± 4%) and 32 ± 3 ms (fraction 78 ± 6%), with no significant difference between the time constants or fractions.

In homomeric α1^Q−26′E receptors, the introduction of a glutamic acid decreased the channel conductance to 60.6 ± 0.4 pS, dramatically increased the mean cluster length to 3161 ± 262 ms, and decreased the intracluster shutting frequency to 15 ± 3 Hz. A comparable pattern of changes was observed in α1^Q−26′E-β heteromers. There was a significant decrease in conductance to 30.8 ± 1.5 pS (Fig. 2C), which is proportional to the decrease measured in the homomeric receptors. The mean cluster duration for α1^Q−26′Eβ heteromers was 893 ± 283 ms, representing a proportional increase relative to the homomeric mutant receptor. The mean frequency of shutting within clusters mediated by α1^Q−26′E-β heteromers was 11 ± 1 Hz. The changes in cluster duration and the intracluster shut events reached significance when compared with wild-type α1β receptors. The MOCs were 258 ± 28 (fraction 82 ± 7%) and 48 ± 7 ms (fraction 77 ± 8%) for the α1^Q−26′E and α1^Q−26′E-β receptors, respectively. The MOC time constant for the α1^Q−26′E homomeric receptors was significantly different from both the wild-type and α1^Q−26′E-β receptors (p < 0.0001).

We infer that the α1^Q−26′E mutation confers four effects on GlyRs. First, receptors bearing this mutation are constitutively active. Second, the decrease in conductance demonstrates that the introduced glutamic acid side group carries a negative charge at pH 7.4, and is close enough to the permeation pathway to influence conductance. Third, the negative charge induces longer duration active periods (and greater MOC time constants) within which the conducting states are more stable. Finally, the β subunit dilutes the effect of the α1^Q−26′E mutation on cluster properties, but not on conductance.

19′ Mutations on an α1^Q−26′E Background

The above results indicate that α1^Q−26′E induces spontaneous openings, but that its effects on ligand-induced cluster duration are reduced when the β subunit is present. This suggests that β subunit residues proximal to α1^Q−26′E may account for the attenuation. To investigate this further, we introduced mutations at 19′ in the α1 and β subunits (Table 1). As with α1^R19′Q receptors, the homomeric α1^R19′A receptors, in the presence of a saturating glycine concentration (50 mm) also showed a significantly reduced conductance (75.0 ± 0.8 pS), a marked decrease in cluster duration to 257 ± 54 ms, a marked leftward shift in the MOC (0.7 ± 0.2 ms, 77 ± 9%), and a substantial increase in shutting frequency (395 ± 18 Hz) compared to the homomeric wild-type (Fig. 3, A and C). Expressing the α1^R19′A on an α1^Q−26′E background produced the α1^{Q−26′E/R19′A} homomeric receptor. Functional impairment was most severe in this double mutant receptor (Fig. 3A). Notably, all spontaneous activity was ablated. Indeed, little activity was observed for these receptors at glycine concentrations below 100 mm. We used 300 mm glycine to induce enough channel activity for analysis. These receptors opened to a conductance of 8.6 ± 0.7 pS, with a mean cluster length of 89 ± 25 ms, an MOC of 1.2 ± 0.2 ms (fraction 83 ± 5%), and a shutting frequency of 292 ± 41 Hz (Fig. 3C).

We then investigated the effect of the reciprocal β subunit mutation in α1β^A19′R GlyRs. When activated by a saturating (1 mm) glycine concentration, this receptor exhibited a small (∼7–8 pS) reduction in conductance (53.7 ± 1.5 pS) and no change to cluster duration (511 ± 179 ms), MOC (30 ± 6 ms, 78 ± 14%), or the frequency of shut events (37 ± 4 Hz) relative to wild-type α1β receptors (Fig. 3, B and D). This demonstrates a functional asymmetry between α1 and β subunits, in accord with a previous report based on whole cell experiments (34). That is, when an arginine residue occupies all five 19′ positions in the mutant heteromeric receptors, the functional parameters of conductance, cluster duration, and number of shut events within clusters are nearly indistinguishable from wild-type heteromers. This is in stark contrast to the effects of removing the arginine in the α1 subunit.

The heteromeric α1^Q−26′E-β^A19′R GlyR also exhibited minimal changes relative to α1^Q−26′E-β receptors. These receptors were constitutively active (Fig. 3B) with a conductance of 29.0 ± 1.5 pS. Glycine (1 mm) elicited clusters with a mean duration of 639 ± 106 ms, an MOC of 69 ± 5 ms (fraction 91 ± 6%), and a shutting frequency of 22 ± 2 Hz. The parameters of conductance, cluster duration, and MOC were not significantly different from the α1^Q-26′E-β receptors (Fig. 3D), whereas there was a small but significant difference in shutting frequency. Together, these data demonstrate the significance of the arginine residue at 19′ in the α1 subunit on receptor activation, in contrast to the β subunit, where the functional influence of this residue is minimal. The existence of spontaneous activity in α1^Q−26′E-β and α1^Q−26′E-β^A19′R receptors implies the presence of at least one α1-α1 interface. Alternatively, α1^Q−26′E may interact with different residues in α1 versus β subunits, giving rise to the observed effects.

24′ Mutations on an α1^Q−26′E Background

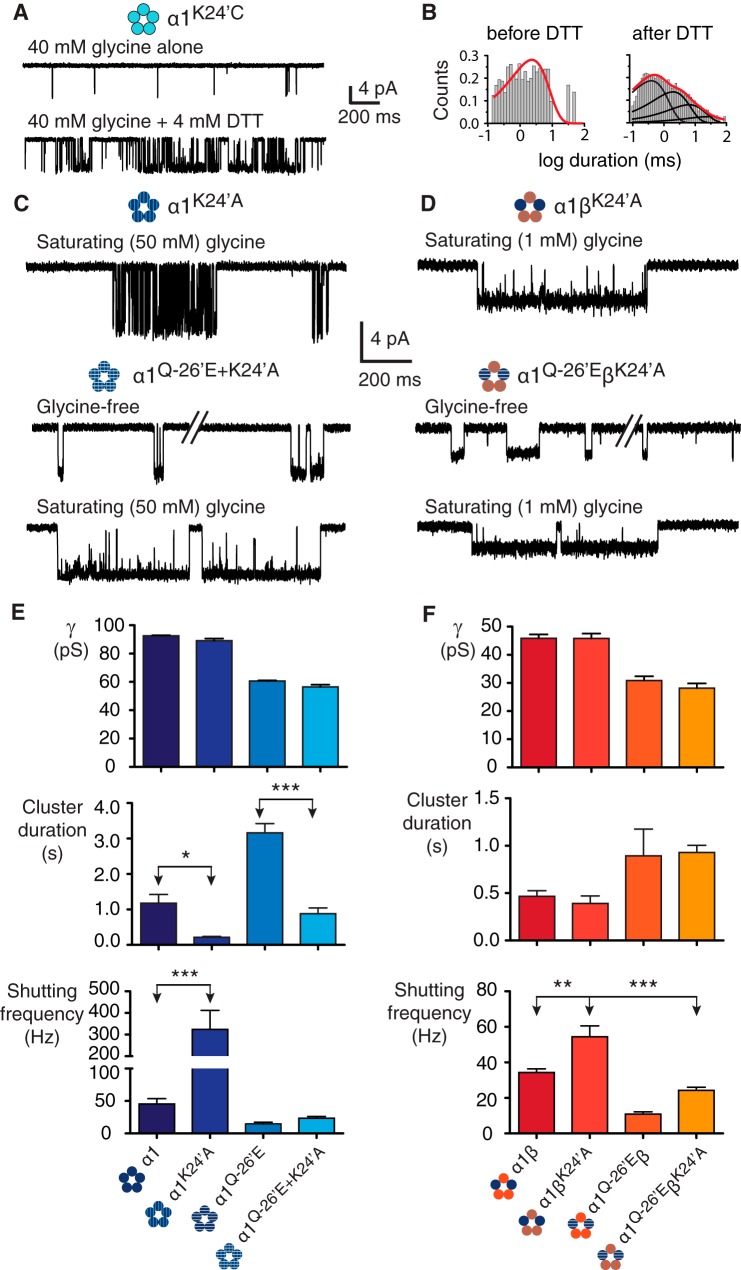
A possible candidate residue that might interact with the α1^Q−26′E residue is Lys²⁴′. This residue is highly conserved, like Arg¹⁹′, has a basic side group, and is critical to efficient channel activation in the α1 subunit (5, 35), especially when mutated to a hyperekplexia-causing glutamic acid (11, 12). Moreover, Lys²⁴′ sits on a segment (the M2-M3 linker) that is mobile enough to permit K24′C cross-linking between α1 subunits in functional GlyRs. This mobility was tested on α1^K24′C homomeric channels (Fig. 4A, Table 1). In the presence of glycine alone, the activations were sporadic and short-lived, as illustrated by the single ∼2 ms open dwell-time component (Fig. 4B, left). Following application of the reducing agent, DTT (4 mm), for a duration of 3–6 min in three patches, the mean burst duration increased dramatically to ∼90 ms and the open dwell-time distributions showed multiple components (Fig. 4B, right). This observation, and the demonstration of H₂O₂-induced reversibility (22) suggests that DTT reduces pre-existing disulfide bonds formed between α1^K24′C residues. No significant difference was detected in conductance for this mutant (90.0 ± 0.5 pS) compared with wild-type, either before or after DTT application. We reasoned that the high amplitude movement of the M2-M3 linker during the activation process could bring Lys²⁴′ close enough to α1^Q−26′E to facilitate interaction between the two. This is also consistent with the pLGIC crystal structures that show proximity between the Lys²⁴′ and −26′ positions (Fig. 1A).

FIGURE 4.

Mutations to 24′. A, α1^K24′C homomeric receptors show evidence of cysteine-cysteine cross-linking. A ∼4 min application the reducing agent DTT (4 mm) resulted in a change in channel activity from infrequent, simple openings to more complex and wild-type-like activations. B, open dwell histograms for the corresponding recordings showing that before DTT the data are fit to a single exponential histogram, whereas after DTT the data are fit to multiple components. C, homomeric α1^K24′A receptors show a reduction in mean cluster duration and an increase in the intracluster shutting frequency. When α1^K24′A is combined with α1^Q−26′E in the same subunit (α1^{K24′A/Q−26′E}), the resulting activations resemble those of the α1^Q−26′E homomers, but with reduced cluster durations. D, heteromeric α1β^K24′A and α1^Q−26′E-β^K24′A receptor activations suggest little effect of the β^K24′A mutation. Bar graphs summarizing the effects on channel conductance, mean cluster duration, and intracluster shutting frequency for homomeric (E) and heteromeric (F) receptors incorporating 24′ mutations. The number of clusters used for homomeric receptors was 124 (α1^K24′A, 4 patches) and 69 (α1^{Q−26′E/K24′A}, 8 patches) and for heteromeric receptors was 114 (α1β^K24′A, 7 patches) and 76 (α1^Q−26′E-β^K24′A, 9 patches). ***, p < 0.0001; **, p < 0.001; *, p < 0.01.

We tested mutant channels that incorporated the K24′A substitution in α1 and β subunits. Representative current traces are shown in Fig. 4, C and D. The first of these was the α1^K24′A homomeric GlyR (Fig. 4C). A saturating (50 mm) glycine concentration induced clusters with a conductance of 89.1 ± 1.6 pS, representing a nonsignificant change compared with α1 wild-type homomers. Greater differences were observed in the kinetic properties of the receptors. Cluster duration and the MOC were an order of magnitude briefer at 214 ± 23 and 3.0 ± 1 ms (fraction 51 ± 1%), whereas the intracluster shutting frequency was an order of magnitude higher at 324 ± 88 Hz (Fig. 4E). The α1^K24′A mutation was then combined with the α1^Q−26′E to produce the double mutant α1^{Q−26′E/K24′A} homomeric receptor. These were active in the absence of glycine (Fig. 4C) and had a similar channel conductance (56.4 ± 1.6 pS) to the α1^Q−26′E homomers. Clusters of activity induced by 50 mm glycine had a mean duration of 882 ± 158 ms and the receptor shut at a frequency of 23 ± 3 Hz while active (Fig. 4F). The MOC for this receptor was 124 ± 26 ms (fraction 96 ± 3%).

Similar experiments were conducted using the equivalent β subunit mutation (β^K24′A), which was initially expressed with the wild-type α1 subunit (Fig. 4D). No significant changes were observed in this receptor in terms of conductance (45.8 ± 1.8 pS), the MOC (30 ± 4 ms, 90 ± 3%), or mean cluster duration (390 ± 81 ms) compared with wild-type heteromeric receptors in the presence of saturating (1 mm) glycine. An influence of the β^K24′A mutation to channel activation was only evident in the increased frequency of shutting, which was 54 ± 6 Hz (Fig. 4F). Heteromers containing α1^Q−26′E and β^K24′A subunits opened to a conductance of 28.1 ± 1.7 pS, which was not significantly different from the α1^Q−26′E-β heteromers. The cluster duration was 929 ± 75 ms and the shutting frequency within clusters was 24 ± 2 Hz (Fig. 4F). The MOC was 72 ± 17 ms (fraction 92 ± 4%), which was significantly increased compared with the wild-type heteromers (p < 0.01), whereas the fraction of the MOC was not. From these data we infer that the effects of the K24′A substitution are smaller than the R19′A substitution in both homomeric and heteromeric receptors. Notably, the minor effects on channel conductance suggest that whereas the channel is conducting current the Lys²⁴′ position is either too far from the permeation pathway to affect conductance or is otherwise neutralized.

The Energetics of α1^R19′, α1^K24′, and α1^Q−26′E Interactions in Homo- and Heteromeric GlyRs

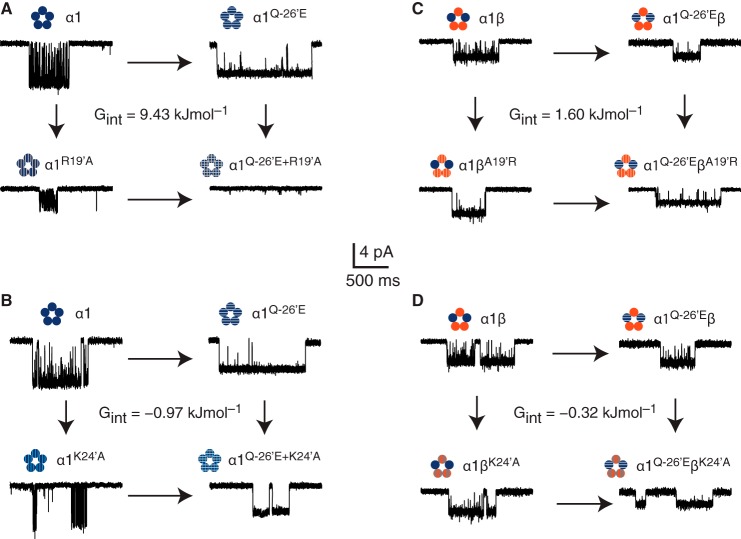
Our data reveal that α1^Q−26′E enhances channel function by conferring spontaneous activity, increasing the time constant of the main open dwell component, lengthening the duration of glycine-induced clusters, and decreasing the transition frequency to shut states while the channel is active. We have assessed the contributions of local electrostatic interactions with 19′ and 24′ residues in both the α1 and β subunits in mediating these effects. We next employed channel conductance and cluster duration in an attempt to define the relative strengths of these interactions in the channel activation process. These parameters were used in mutant cycle calculations for four potential interaction partner combinations involving the α1^Q−26′E residue (Fig. 5). The first of these was the α1^Q−26′ and α1^R19′ cycle. This revealed an interaction energy of 9.43 kJ mol⁻¹ (2.3 kcal mol⁻¹) (Fig. 5A). The energy of interaction between α1^Q−26′ and α1^K24′ was −0.97 kJ mol⁻¹ (−0.23 kcal mol⁻¹) (Fig. 5B). The coupling energies involving heteromers were lower than for homomeric receptors. The α1^Q−26′-β^A19′ cycle yielded an interaction energy of 1.60 kJ mol⁻¹ (0.38 kcal mol⁻¹) (Fig. 5C), whereas the interaction energy for the α1^Q−26′ and β^K24′ was the lowest, being −0.32 kJ mol⁻¹ (−0.08 kcal mol⁻¹) (Fig. 5D). Table 2 shows ΔΔG_int calculations using other kinetic parameters, in addition to the product of cluster duration and conductance. These include the use of cluster duration and conductance, separately, the product of the cluster duration and open state probability (P_o), and the MOC time constant for each receptor. Overall, these data show that interactions between −26′ and the 19′ and 24′ positions are strongest in α1 homomeric receptors, especially the interaction between α1^Q−26′ and α1^R19′. Introducing the β subunit, even one bearing an arginine at 19′ did not increase the strength of interactions with α1^Q−26′E, even though we predict a majority of α1-β subunit interfaces in heteromeric GlyRs (26, 27). Interactions between the −26′ and 24′ side groups in both subunits were weaker, but not negligible in the α1 subunit. The especially weak interaction energy between α1^Q−26′ and β^K24′ supports the notion that the TZ of the β subunit is of lesser significance in receptor activation than the α1 subunit.

FIGURE 5.

Energetic interactions between −26′ and 19′ or 24′. Mutant cycle analysis for interactions between −26′ and 19′ (A) and the −26′ and 24′ (B) in homomeric, and −26′ and 19′ (C) and the −26′ and 24′ (D) in homomeric GlyRs. Each mutant cycle is accompanied by sample recordings of each receptor and the calculated interaction energy (ΔΔG_int).

Generality of −26′, 19′, and 24′ Interactions Across the pLGIC Family

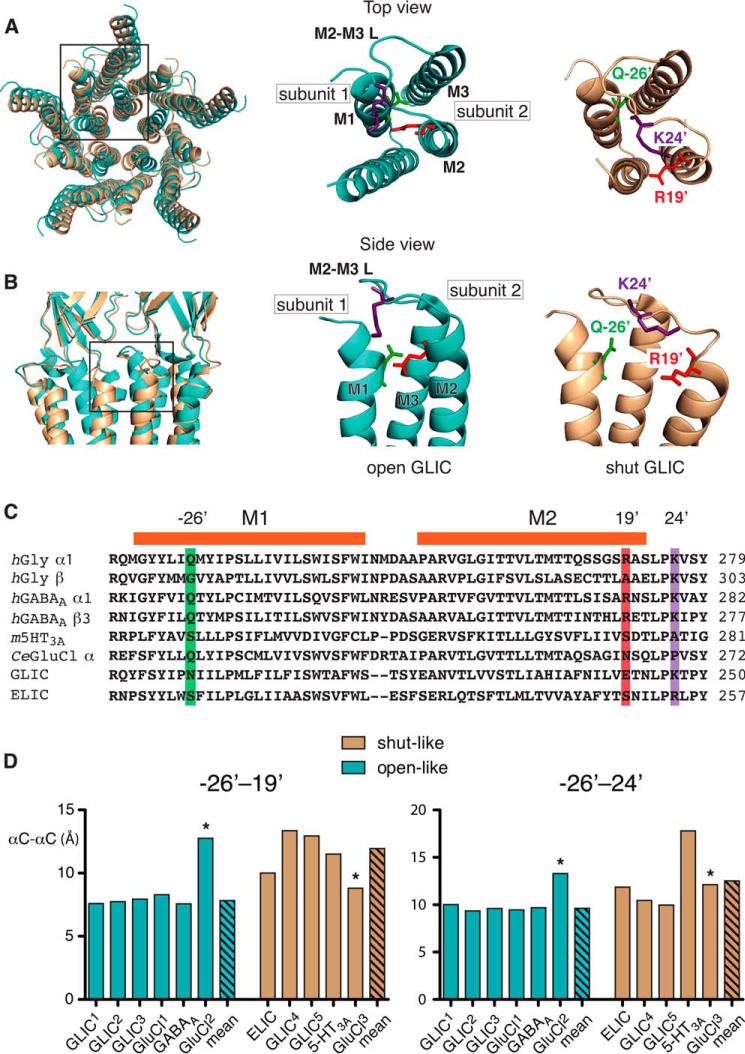
In recent years high-resolution structures of several members of the pLGIC family in putative current conducting and non-conducting states have become available. These include different species of prokaryotic (15, 17–19) and eukaryotic (14, 16, 20, 21) pLGICs. Given that these structures are static representations obtained under non-physiological conditions, it is vital to check them against functional data to ascertain if the crystal structures correspond to functionally relevant states. It is also useful to determine whether the putative interactions identified here are likely to have universal relevance across the pLGIC family. A structural alignment of two GLIC structures, in open (18) and closed (19) states (Fig. 6, A and B) reveals relative movements of the residues at −26′, 19′, and 24′ during channel opening.

FIGURE 6.

Spatial relationship between −26′, 19′, and 24′ in pLGICs of known structure. Superposition of top (A) and side (B) views of GLIC in putative open (cyan, Protein Data Bank code 3EHZ) and shut (beige, Protein Data Bank code 4NPQ) configurations showing the relative separation between positions, −26′, 19′, and 24′. Boxed regions showing the TDs of the open and shut structures with the first (M1) transmembrance domain of one subunit and the Gln⁻²⁶′ residue (green), and the second (M2) and third (M3) transmembrane domains of the adjacent subunit with Arg¹⁹′ (red) and Lys²⁴′ (purple). The M2-M3 linker (M2-M3 L) is also shown. C, sequence alignment covering the region under investigation of selected pLGICs. Highlighted are the −26′, 19′, and 24′ positions. The prefixes on the sequence labels denote, human (h), mouse (m), and Caenorhabditis elegans (Ce). Included are the sequences of GLIC (Gloeobacter violaceus) and ELIC (Erwinia chrysanthemi). D, bar plots of the Cα-Cα distances between the −26′ and 19′ and −26′ and 24′ positions obtained from the indicated crystal structures. The measurements were taken from the following Protein Data Bank files, in parentheses, GLIC¹ (3EHZ), GLIC² (3EAM), GLIC³ (3UU5), GLIC⁴ (3UU3), GLIC⁵ (4NPQ), ELIC (2VLO), GluCl¹ (3RIF), GluCl² (4TNW), GluCl³ (4TNV), GABA_A (4COF) and 5-HT_3A (4PIR). Asterisks denote outlier values (GluCl² and GluCl³) that were omitted from the means.

To determine whether the interactions examined in this study represent a universal structural principal of pLGIC activation we measured the α-carbon-α-carbon (αC-αC) distances between the −26′ and 19′ positions and the −26′ and 24′ positions (Fig. 6C) in crystal structures of pLGICs in putative conducting and non-conducting configurations (Fig. 6D). Inclusion of structures in either the open-like or closed-like groups was based on a consideration of several features of each structure, including the minimum pore diameter, M2 orientation, and the molecules in which each receptor was co-crystalized. In each case, our classifications are in accord with those proposed by the original authors.

The residues at positions −26′ and 19′ have a significantly smaller mean αC-αC distance in conducting states (7.8 ± 0.1 Å) compared with nonconducting ones (12.9 ± 1.0 Å). The mean distance between positions −26′ and 24′ differs less between the two states, with a nonsignificant decrease from 12.9 ± 2.2 (nonconducting) to 9.7 ± 0.1 Å (conducting). The distances between −26′ and 19′, and −26′ and 24′ from a recently published GluCl structure in apo (closed) and POPC-bound confirmations (open) were excluded from the mean distance calculations (14). The decision to exclude these data were made on the basis that the αC-αC distances from −26′ to 19′ or 24′ were clear outliers, especially for −26′ to 19′. Furthermore, the POPC-bound (presumably open) structure differs from an earlier ivermectin- and glutamate-bound structure (16) in terms of the distances measured, and this earlier structure does conform to the general trends observed. This suggests that the apo and POPC-bound structures might not resemble physiological conformations, and so were excluded from further analysis.

Prediction of Synaptic Currents Mediated by α1^Q−26′E-containing GlyRs

Finally, we investigated how the α1^Q−26′E hyperekplexia mutation might affect glycinergic inhibitory synaptic currents. Applying a saturating (1 mm) glycine concentration for brief periods (<1 ms) to outside-out membrane patches containing many receptors elicited synaptic-like ensemble currents. Wild-type α1 homomers and α1β heteromers activated rapidly, with 10–100% rise time constants of 0.24 ± 0.06 and 0.24 ± 0.02 ms, respectively. The decay time constants were also relatively brief, being 24.2 ± 7.3 ms for homomers and 15.7 ± 4.3 ms for heteromers (Fig. 7A). The β subunit had no significant influence on either parameter. Our results are consistent with those measured previously via similar techniques (36) and with synaptic currents of native synapses expressing α1 homomeric and α1β heteromeric GlyRs (37). This similarity in kinetics suggests that they are dominated by the α1 subunit. This inference was borne out in our experiments on α1^Q−26′E homomers and α1^Q−26′E-β heteromers. Currents mediated by both receptors containing the α1^Q−26′E mutation were activated with rise time constants that were similar to wild-type receptors. These were 0.26 ± 0.03 and 0.31 ± 0.09 ms for homo- and heteromeric receptors, respectively. The decay time constants measured from α1^Q−26′E and α1^Q−26′E-β receptors were an order of magnitude greater compared with their respective wild-type receptors (280 ± 41 and 272 ± 35 ms, respectively) and were not significantly different from each other (Fig. 7A).

FIGURE 7.

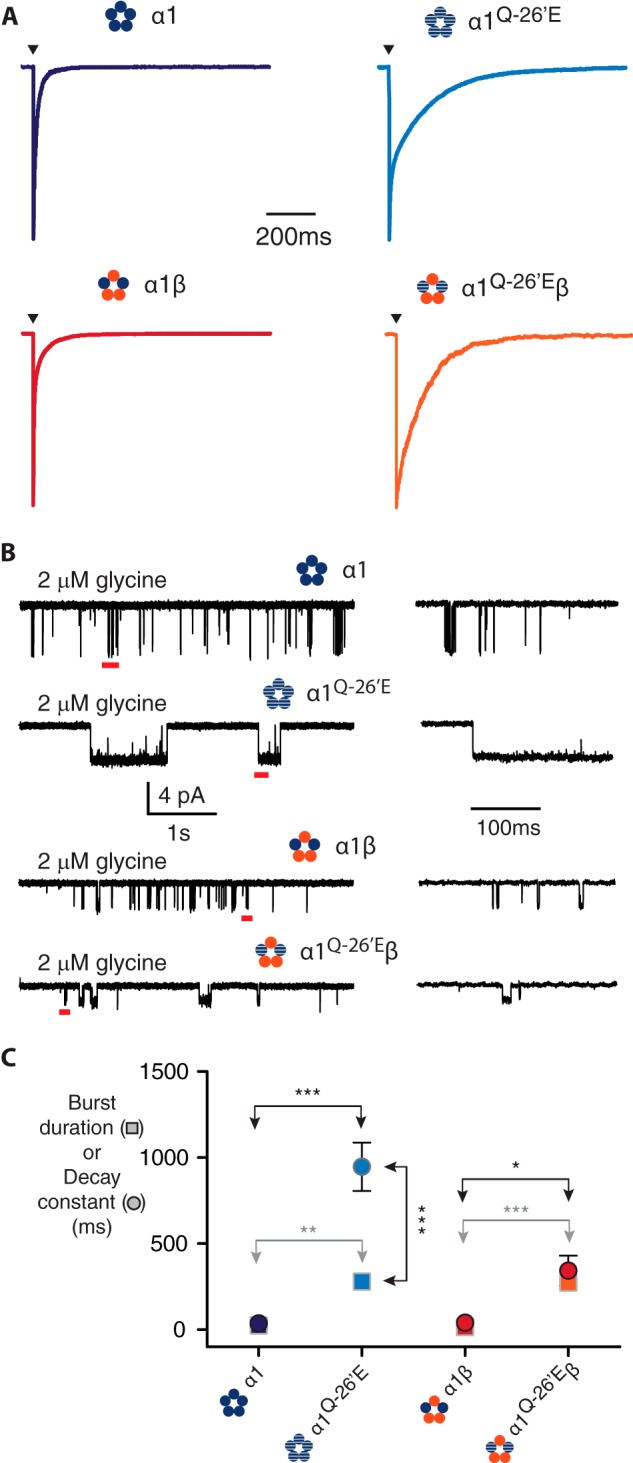
Synaptic-like ensemble currents and burst durations in α1^Q−26′E-containing homo- and heteromeric GlyRs. A, sample ensemble currents recorded from outside-out patches containing the indicated receptors. The currents were elicited by brief (<1 ms) exposure to saturating (1 mm) glycine. Note the slower rates of current decay for currents mediated by α1^Q−26′E-containing receptors. B, sample single channel recording in the presence of 2 μm glycine for the indicated receptors. The segments of record marked by a red bar are shown in expanded view on the left. C, mean values of burst duration (circles) and corresponding decay rates (squares) for the receptors in A and B. The number of bursts used in the analysis was 296 (α1 wild-type, 6 patches), 227 α1β (wild-type, 5 patches), 165 (α1^Q−26′E, 7 patches), and 450 (α1^Q−26′E-β, 5 patches). The number of patches used for the macropatch recordings was 5 (α1 wild-type), 9 α1β (wild-type), 11 (α1^Q−26′E), and 3 (α1^Q−26′E-β). ***, p < 0.0001; **, p < 0.001; *, p < 0.01.

It has been demonstrated that the time constant for deactivation of ensemble currents is the same as the burst durations at very low concentrations of ligand (38). However, it is difficult to predict what a sufficiently low concentration of glycine would be that might elicit burst durations that correspond to the measured decay times. We thus employed 2 μm glycine to activate bursts of activity from wild-type and α1^Q−26′E-containing homomers and heteromers (Fig. 7B). 2 μm glycine induced bursts of activity in α1^Q−26′E-containing receptors that were of longer duration compared with their wild-type counterparts. Wild-type α1 homomers were activated for a mean of 37 ± 4 ms, whereas the mean burst duration of α1^Q−26′E homomeric receptors was 947 ± 141 ms. Wild-type heteromers had a mean burst duration of 40 ± 3 ms and heteromers incorporating the α1^Q−26′E mutation had a mean burst duration of 344 ± 87 ms. The mean burst durations and ensemble current decay times were plotted on the same set of axes to investigate any correlation between them (Fig. 7C). A closer correspondence between burst duration and decay times was observed for wild-type receptors, the former quantity being ∼1.5–2.5-fold greater than the latter. For receptors containing the α1^Q−26′E mutation there was greater deviation between the burst duration and current decay times, especially for α1^Q−26′E homomers. We make the following inferences from these data. First, that current kinetics in homo- and heteromeric receptors are dominated by the α1 subunit. Second, that there is a strong correlation between the burst duration and the decay rate of ensemble currents. Third, that 2 μm glycine is likely too high a concentration to elicit bursts that are sufficiently brief to account for the current decay times, especially for mutant-containing receptors. Fourth, that synaptic currents in vivo mediated by GlyRs expressing the α1^Q−26′E mutation will decay dramatically more slowly than wild-type.

DISCUSSION

Our aim was to investigate the mechanism by which the α1^Q−26′E mutation induces spontaneous activity in homo- and heteromeric GlyRs on the level of single receptors. We reasoned that insights thus obtained may be used in conjunction with crystal structures of several, newly published pLCIC members to provide fundamental insights into the activation mechanisms of pLGICs in general. We investigated these receptors via single-channel analysis for two reasons. First, single channel kinetic analysis permits a quantitative understanding of the channel gating process and its underlying energetics (39, 40). Second, single channel conductance analysis allows us to determine whether mutations to residues near the pore lumen alter side group charge (24, 41). This would help us to resolve whether electrostatic interactions among the mutated residues affect receptor activation. The correlation between conductance and cluster length was critical for the interpretation of pairwise interactions because if a mutation did not affect conductance it also had no effect on cluster duration on receptors containing the α1^Q−26′E as a background. The importance of connecting cluster duration and conductance becomes clearer when comparing the α1^{Q−26′E/R19′A} receptors with α1^{Q−26′E/K24′A}, α1^Q−26′E-β^K24′A, or α1^Q−26′E-β^A19′R receptors. The α1^R19′A mutation decreases cluster duration and conductance on a wild-type background, and on an α1^Q−26′E background. In contrast, the α1^K24′A decreases cluster duration but not conductance. The α1^{Q−26′E/K24′A} double mutations had no additional effect on either parameter. The β^K24′A or β^A19′R mutations had no significant effects on cluster duration or conductance when co-expressed with either α1 wild-type or α1^Q−26′E. These observations support the notion that α1^K24′ is a salient gating element, but not as part of the α1^Q−26′-α1^R19′ pathway, whereas β^24′ or β^19′ positions seem not to support charge nor do they feature prominently in receptor activation.

Our finding that α1^Q−26′E-β, α1^Q−26′E-β^K24′A, and α1^Q−26′E-β^A19′R receptors are also spontaneously active in conjunction with high α1^−26′-α1^19′ coupling energy implies the presence of at least one α1-α1 interface. The stoichiometry of α1β GlyRs is in dispute, with some studies finding evidence for a 3α:2β ratio (42, 43) and others for a 2α:3β ratio (26, 27). If α and β subunits alternate in the pentamer, as proposed by both the Grudzinska and Yang studies (26, 27), the presence of at least one α1-α1 interface necessitates a 3α:2β ratio. This in turn implies that a single α1^−26′-α1^19′ electrostatic bond per pentamer in α1^Q−26′E-containing receptors is sufficient to induce spontaneous activity and enhance the duration of ligand-induced activations.

Assuming that the coupling energies calculated here reflect relative degrees of local conformational movements necessary for the receptor to transition between stable functional states, we can deduce the following about GlyR (and other pLGIC) activation. The TZ of the α1 subunit is the most mobile, especially the extracellular portions of M1, M2, and the M2-M3 linker, compared with the TZ of the β subunit. The mean increase in proximity between α1^−26′ and α1^19′, between putative non-conducting and conducting states derived from crystal structures is greatest (>5 Å, Fig. 6). So too, is the ΔΔG_int for this interaction in the α1 subunit (Fig. 5). The α1^−26′-α1^19′ coupling energy is well within the range for a significant interaction between residues in pLGICs during activation (39, 40, 44) and between ligand binding residues and ligand (45). We propose that this interaction represents one point of energy transfer along what is likely to be a broad reaction coordinate (broad corrugated activation barrier) as proposed by Auerbach for the related nAChR (40, 46).

The cross-linking evidence suggests that the α1 M2-M3 linker is also highly mobile. This mobility is evidently necessary to produce activations that exhibit the type of complexity (multiple dwell components, Fig. 4) characteristic of wild-type receptors (12, 47). However, the mean change in separation between −26′ and 24′ between conducting and non-conducting states is less than that for −26′ and 19′ (∼3 Å), and the absolute distance between these two positions is greater (Fig. 6). The relatively low coupling energy associated with α1^−26′ and α1^24′, along with evidence that α1^24′ mutations lead to profound perturbations in receptor activation suggests that this residue (and likely the M2-M3 linker) is involved in a different route of energy transfer to that of α1^−26′ and α1^19′. The α1^K24′ may interact with aromatic residues in the β10-M1 linker (Fig. 1A, inset) to form cation-π contacts, as predicted by the crystal structure of the β3 homomeric GABA_A receptor (21).

The coupling energies calculated for α1^−26′ with β^19′ and β^24′ parallel those for the α1 subunit alone. However, the corresponding values suggest either weak or no interactions. This is reconcilable with the notion that the β subunit has a subordinate role in receptor activation (34). Moreover, adding a basic residue at β^19′ or removing one from β^24′ had little or no effect on channel conductance, respectively. These data suggest that the microenvironment around these positions is such that basic residues are weakly protonated (24), or otherwise not felt by permeating ions. β^24′-β^24′ cysteine cross-linking is not amenable to electrophysiology, but an α1^−26′-β^24′ coupling energy that is comparable with the thermal energy of the receptor (40) would imply the βM2-M3 linker is relatively static with respect to α1^−26′ during receptor activation. Together, these findings imply that many parts of the receptor change energy during activation.

We have demonstrated that the increased duration of unliganded (spontaneous) activity was paralleled by an increase in the durations of fully liganded activity (clusters) in receptors containing the α1^Q−26′E mutation. This is also the case for wild-type receptors. From this observation we infer that the α1^Q−26′E mutation has not uncoupled the activation mechanism as it occurs in wild-type receptors, allowing the transmembrane domains to adopt open, conducting conformation(s) by autonomously interacting with α1^R19′. The indistinguishable conductance levels between unliganded and fully liganded receptors lend support to this inference (48, 49). Furthermore, we infer that by enhancing the α1^−26′-α1^19′ interaction, the α1^Q−26′E mutation has exposed a salient component of the activation mechanism of the wild-type receptor. If we assume that the receptors are in thermodynamic equilibrium, and that the ligand binding properties of receptors mutated at the TZ are little changed relative to wild-type (12, 50), then it follows that for an increase in the activation equilibrium constant for unliganded activation (an index of the efficacy with which the receptor transitions from non-conducting to conducting configurations) there will be a corresponding increase in the fully liganded activation equilibrium constant. This result has been well documented for constitutively active muscle nAChRs that bear mutations within the TZ (49, 51).

In summary, we sought to quantitate the strength of interactions between the 19′, 24′, and −26′ positions in contributing to the activation mechanism of both homo- and heteromeric GlyRs. We conclude that the α1^−26′-α1^19′ interaction is likely part of a significant pathway that distributes the energy of ligand binding to receptor activation. The significance of the interaction was made evident by the discovery that a single electrostatic interaction per α1^Q−26′E-containing pentamer is sufficient to enhance receptor activation. The 24′ position, although situated on a segment that is also highly mobile, is likely involved in a different energetic pathway. The local movements associated with these energetic interactions are evident in published crystal structures, indicating that they may pertain widely across the pLGIC family.