Significance
Quantifying a network's link predictability allows us to (i) evaluate predictive algorithms associated with the network, (ii) estimate the extent to which the organization of the network is explicable, and (iii) monitor sudden mechanistic changes during the network's evolution. The hypothesis of this paper is that a group of links is predictable if removing them has only a small effect on the network's structural features. We introduce a quantitative index for measuring link predictability and an algorithm that outperforms state-of-the-art link prediction methods in both accuracy and universality. This study provides fundamental insights into important scientific problems and will aid in the development of information filtering technologies.
Keywords: link prediction, complex networks, structural perturbation, predictability
Abstract
The organization of real networks usually embodies both regularities and irregularities, and, in principle, the former can be modeled. The extent to which the formation of a network can be explained coincides with our ability to predict missing links. To understand network organization, we should be able to estimate link predictability. We assume that the regularity of a network is reflected in the consistency of structural features before and after a random removal of a small set of links. Based on the perturbation of the adjacency matrix, we propose a universal structural consistency index that is free of prior knowledge of network organization. Extensive experiments on disparate real-world networks demonstrate that (i) structural consistency is a good estimation of link predictability and (ii) a derivative algorithm outperforms state-of-the-art link prediction methods in both accuracy and robustness. This analysis has further applications in evaluating link prediction algorithms and monitoring sudden changes in evolving network mechanisms. It will provide unique fundamental insights into the above-mentioned academic research fields, and will foster the development of advanced information filtering technologies of interest to information technology practitioners.
Understanding the organization of real networks is a long-standing challenge in many branches of science (1). Although some mechanisms have already been accepted as primary driving forces in network organization, including homophily (2–4), triadic closure (5–7), preferential attachment (8–10), reciprocity (11), and social balance (12), one or two of these mechanisms cannot provide a complete explanation; i.e., link formation in real-world networks is usually driven by both regular and irregular factors, and only the former can be explained using mechanistic models. This intrinsic network complexity presents us with the question of how to estimate what portions of a real network can be categorized as regular, in other words, to what extent the link formation in network is explicable.
This question brings to mind the link prediction problem in which the set of observed links in a network is used to estimate the likelihood that a nonobserved link exists (13). The extent to which the network formation is explicable coincides with our capacity to predict missing links (14, 15). On the one hand, an effective link prediction algorithm provides strong evidence of the corresponding mechanism(s) of network organization, e.g., effectiveness of common-neighborhood-based methods indicates the significance of triadic closure (16, 17). On the other hand, a better understanding of network organization should be transferable to a good link prediction algorithm, e.g., the prior assumption of hierarchical organization of networks can be directly applied to the design of a prediction algorithm (18). In this sense, the precision of a link prediction algorithm tells us the extent to which the link formation in network can be explained by this algorithm. However, different algorithms provide different precisions in same network (see Table 1, the precisions of seven link prediction (LP) methods on 10 networks) and thus the precision only reflects the link predictability associated with a specific algorithm, not the intrinsic feature of the network itself.
Table 1.
Link prediction accuracy measured by precision on the 10 real networks
| Precision | Jazz | Metabolic | Neural | USAir | Food web | Hamster | NetSci | Yeast | Router | |
| SPM | 0.677 | 0.354 | 0.168 | 0.451 | 0.561 | 0.469 | 0.334 | 0.166 | 0.158 | 0.357 |
| CN | 0.506 | 0.137 | 0.095 | 0.374 | 0.073 | 0.061 | 0.329 | 0.109 | 0.149 | 0.027 |
| AA | 0.525 | 0.190 | 0.105 | 0.394 | 0.075 | 0.061 | 0.334 | 0.121 | 0.150 | 0.026 |
| RA | 0.541 | 0.267 | 0.104 | 0.455 | 0.076 | 0.054 | 0.541 | 0.090 | 0.148 | 0.027 |
| Katz | 0.546 | 0.147 | 0.107 | 0.379 | 0.181 | 0.108 | 0.370 | 0.061 | 0.149 | 0.120 |
| HSM | 0.326 | 0.100 | 0.073 | 0.216 | 0.249 | 0.202 | 0.303 | 0.081 | 0.134 | 0.309 |
| SBM | 0.410 | 0.197 | 0.143 | 0.335 | 0.460 | 0.275 | 0.177 | 0.122 | 0.094 | 0.176 |
We compare our method, SPM, to six well-known methods presented in Materials and Methods. For each real network, 10% of its links will be randomly selected to constitute the probe set, and the rest of the links constitute the training set. Prediction accuracy is measured by precision. We set for SPM. For the parameter-dependent Katz index, the present results correspond to the optimal parameter subject to the highest precision. The highest value for each network is in boldface.
Predictability is usually defined as the possible maximum precision of a prediction algorithm (19). However, this kind of definition is not suitable for link prediction since a real network’s link predictability under such definition should be 1 because their nonobserved links are almost always distinguishable (see Materials and Methods). In this paper, link predictability indeed characterizes the inherent difficulty of prediction that does not depend on specific algorithms, and our fundamental hypothesis is that missing links are difficult to predict if their addition causes huge structural changes, and thus network is highly predictable if the removal or addition of a set of randomly selected links does not significantly change the network’s structural features. Accordingly, we propose a so-called “structural consistency” index that is based on the first-order matrix perturbation, which can reflect the inherent link predictability of a network and does not require any prior knowledge of the network’s organization. We also propose a structural perturbation method for link prediction that is more accurate and robust than the state-of-the-art methods.
Structural Consistency
Consider a simple undirected network where V is the set of nodes and E is the set of links. The given network can be represented by an adjacency matrix A, where the element if nodes i and j are connected and otherwise. We randomly select a fraction of the links to constitute a perturbation set , while the rest of the links constitute the set . Denote by and the corresponding adjacency matrices; obviously, . Since is real symmetric, it can be diagonalized as
| [1] |
where and are the eigenvalue and the corresponding orthogonal and normalized eigenvector for , respectively.
We consider the set as a perturbation to the network and construct the perturbed matrix via first-order approximation that allows the eigenvalues to change but fixes the eigenvectors. We first consider the nondegenerated case without any repeated eigenvalues (see SI Appendix, Case of Degenerate Eigenvalues, for the case with degenerate eigenvalues). After perturbation, the eigenvalue is corrected to be and its corresponding eigenvector is corrected to be . Left-multiplying the eigenfunction
| [2] |
by and neglecting second-order terms and , we obtain
| [3] |
This formula is reminiscent of the expectation value of the first-order perturbation Hamiltonian in quantum mechanics. Using the perturbed eigenvalues while keeping eigenvectors unchanged, the perturbed matrix can be obtained,
| [4] |
which can be considered as the linear approximation of the given network A if the expansion is based on .
The eigenvectors can well reflect network structural features (20). If the perturbation does not significantly change the structural features, the eigenvectors of the observed matrix (i.e., ) and those of the matrix (i.e., ) should be almost the same. If so, according to Eq. 4, should be very close to . Therefore, given a network A, we first randomly remove a group of randomly selected links , and then we perturb the remaining part by to obtain the perturbed matrix via Eq. 4. If the network is highly regular, the random removal will not sharply change the structure features, and thus A and should be close to each other. To measure this quantitatively, we rank all of the links in set in descending order according to their values in , where U is the universal set of links. We denote the set of top-L ranked links, where , namely, the number of links in the perturbation set. Then the links in together with the links in construct the perturbed network, which is usually different from . The structural consistency is defined as the fraction of common links between and , as
| [5] |
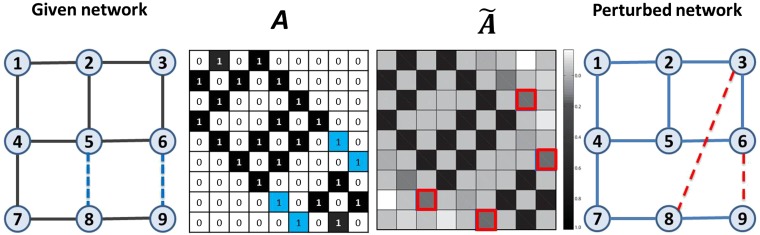
Fig. 1 shows how to calculate the structural consistency of a simple network, with a summary of detailed procedure presented in SI Appendix, Six Steps to Calculate σc.
Fig. 1.
An illustration of how to calculate the structural consistency. In the first plot, the blue dashed links constitute the perturbation set (corresponding to ), while the solid links constitute the set (corresponding to ). The second plot shows the adjacency matrix A of the given network, where the number in each square is the corresponding value of the matrix element. The black and blue squares represent the links in and , respectively. To calculate the consistency, we perturb with . The perturbed matrix is shown in the third plot, from which we derive the perturbed network in the fourth plot, where the red dashed lines are outcome links selected by ranking all links in in descending order according to their corresponding values in . Since there are two links in , then , and the set . In this case, only one of the two blue links is recovered by perturbation; then we have .
Structural Perturbation Method
The perturbation method used to determine the structural consistency can be applied to predict missing links. Link prediction aims at estimating the existence likelihood of nonobserved links based on the observed topology (13). The simplest framework of link prediction is similarity-based algorithms (16) in which each pair of nodes, x and y, is assigned a similarity score . All nonobserved links are ranked according to their scores, with an assumption that links with higher scores have higher existence likelihoods (see mathematical description of LP problem as well as the accuracy metrics in SI Appendix, Link Prediction Problem). Under this framework, the entries of can be considered as the similarity scores assigned to links. For example, in Fig. 1, if we want to predict one missing link of given network A by using the structural perturbation method (SPM), we will rank all of the nonobserved links (i.e., the links corresponding to 0 in matrix A) according to their scores in ; then the top one is the link (3,8). The feasibility of SPM is based on the strong correlation between independent perturbations (see SI Appendix, Table S1), which indicates that the missing links, which are considered as unknown information, can be recovered by perturbing the network with another set of known links (i.e., ).
Consider an undirected network : To test the algorithm’s accuracy, the set of links, E, is randomly divided into two parts: (i) a training set , which is treated as known information, and (ii) a probe set (i.e., validation subset) , which is used for testing and can be considered as missing links. No information in the probe set is allowed to be used for prediction. Obviously, and . Our task is to uncover the links in the probe set based on the information in the training set.
Notice that, in this task, the training set plays a similar role to the observed network A, and to obtain the perturbed matrix , we randomly select a fraction of links from as perturbation set . Then, by perturbing with , we obtain through Eq. 4. The final average prediction matrix is obtained by averaging over 10 independent selections of . By ranking all of the nonobserved links (i.e., links in ) in decreasing order according to their scores given by , we select the top- links and see how many of them are in the probe set. This ratio is called “precision,” which is used to quantify the performance of the algorithm (21). A summary of detailed procedures can be found in SI Appendix, Five Steps to Calculate Prediction Accuracy of SPM.
We compare the structural perturbation method with six widely applied link prediction algorithms, including four similarity-based indices: the common neighbors (CN) index (16), the Adamic-Adar (AA) index (22), the resource allocation (RA) index (17, 23), and the Katz index (24). We also use two likelihood methods: the hierarchical structure model (HSM) (18) and the stochastic block model (SBM) (25). See Materials and Methods for the six baseline algorithms. Table 1 shows the prediction accuracy of the 10 real-world networks (see Materials and Methods and SI Appendix, Table S2, for the description and basic statistics of the data), measured by precision [see SI Appendix, Table S3 for the results measured by another metric called AUC: the area under the receiver operating characteristic curve (26); see the definition in SI Appendix, Link Prediction Problem, Eq. 5]. The highest value for each network (in each column) is in boldface. Overall, SPM outperforms all other baseline algorithms including such state-of-the-art methods as the RA index, HSM, and SBM. In addition, SPM is the most robust method for disparate networks; i.e., although, in a few cases, its performance is not the best, it is always very good. In contrast, all six baseline algorithms give very poor predictions for some networks. In addition to the effectiveness of SPM, we can efficiently obtain an approximate result by sampling large-scale networks (see discussion in SI Appendix, Applying to Large Networks).
Notice that the random division of and is relevant to the prediction of missing parts of networks, such as protein−protein interaction networks where the known interactions are even fewer than unknown interactions (27). In addition to the prediction of missing links in static networks, LP algorithms can also predict future links in evolving networks, such as friendship recommendations in online social networks. In such issues, to evaluate the algorithmic performance, observed links should be divided according to their birth times: Elder (90%) and younger (10%) links constitute and , respectively. We have also tested LP algorithms in three real evolving networks (see Materials and Methods and SI Appendix, Table S2); as shown in Table 2, SPM still performs the best.
Table 2.
The precision of link prediction on three real-world temporal networks
| Networks | CN | AA | RA | Katz | HSM | SPM |
| Arxiv | 0.021 | 0.022 | 0.026 | 0.033 | 0.020 | 0.085 |
| 0.021 | 0.024 | 0.041 | 0.022 | 0.007 | 0.051 | |
| Enron | 0.032 | 0.033 | 0.027 | 0.033 | 0.008 | 0.033 |
Each network is of size N = 4,000, that sampled from the original networks by using the random-walk method (see SI Appendix). The best-performed entries are emphasized in bold. We set for SPM and for the parameter-dependent Katz index; the present results are obtained under the optimal parameter subject to the highest precision. The results of SBM are not included due to the high computational complexity.
Link Predictability
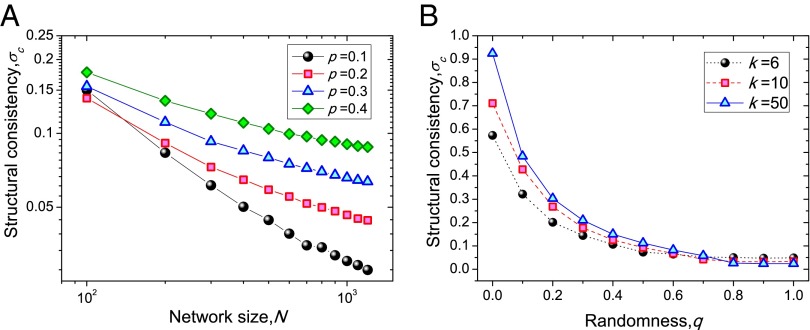
We first consider the structural consistency of modeled networks and show the validity of as an index for link predictability. In the Erdös−Rényi (ER) network (28), each pair of nodes is connected with probability p. If p is finite and the network size N goes to infinity, the spectral density adjacency matrices in ER networks obey the Wigner semicircle law and the eigenvectors are distributed isotropically at random (29, 30). The first-order perturbation of the eigenvalues is thus also random, leading to low structural consistency values. Given an ER network , we randomly select a fraction of the links (we have tested that is not sensitive to the specific value of ; see SI Appendix, Fig. S3), and determine the average structural consistency as a function of N for different p. Fig. 2A shows how the structural consistency decreases with the network size in a power-law-like relationship and tends to the random chance in the thermodynamical limit, supporting the intuition that fully random networks are unpredictable, which is also in accordance with the previous report about the very low link prediction accuracy on ER networks (31).
Fig. 2.
Structural consistency of modeled networks: (A) ER networks with different sizes N and connecting probabilities p; (B) WS networks with N = 1,000, and different average degrees k and rewiring probabilities q. Each data point is averaged over 100 independent runs.
We next consider the Watts−Strogatz (WS) networks (32) with controllable randomness. A WS network starts from a ring of N nodes where each node connects to its k nearest neighbors. With a probability q, each link is replaced by another link that joins two randomly chosen nodes. When , the network is a deterministic ring, and when , it is fully random. Fig. 2B shows how decreases with the rewiring probability q, indicating once again that higher irregularities (i.e., randomness) will result in lower predictability.
The above experimental results on modeled networks affirm the rationale behind the proposed index . We next turn our attention to real-world networks, whose predictabilities cannot be controlled as WS networks. We thus compare the structural consistency with the prediction accuracy from representative link prediction algorithms. Table 3 shows how the prediction precision is positively correlated with structural consistency for all six baseline algorithms, indicating that can, to some extent, reflect the link predictability of real networks. In addition, the precision values of algorithms that account for the global organization principles are approximately linearly correlated with the structural consistency (as indicated by >0.8 Pearson correlation coefficients in Table 3; see also Fig. 3), suggesting that the structural consistency is indeed a good indicator of whether the network is organized by some perceptible regulations. The results also show us that the missing links in networks with higher structural consistencies are easier to dig out using link prediction algorithms.
Table 3.
Pearson correlation coefficients (CC) between precision and structural consistency on the 10 real networks
| CN | AA | RA | Katz | HSM | SBM | SPM | |
| CC | 0.493 | 0.476 | 0.495 | 0.698 | 0.870 | 0.819 | 0.938 |
Fig. 3.
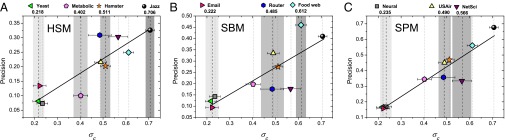
Scatter plot between structural consistency and precision of SPM, SBM, and HSM. The numbers on the top of the panels are the structural consistencies of the corresponding networks obtained at , averaged over 10 independent runs. The error bars represent the SDs of . The shadows in the background emphasize the structural consistencies of the corresponding networks. The higher is, the darker the corresponding shadow region is. The solid lines are the linear fittings with slopes being equal to 0.957, 0.598, and 0.495 for (C) SPM, (B) SBM, and (A) HSM, respectively.
Discussion
Throughout history, human beings, from ancient prophets to modern scientists, have attempted to make predictions. The recent development of theoretical tools and the expanding availability of massive databases have allowed scientists to predict behaviors and trends, chart emergent events, and locate missing elements of a system (33–35). In this paper, we treat predictability as an inherent measurement of the regularities in the organization of a networked system, and our hypothesis is that a missing part is predictable only when it does not significantly change the structural features of the observable part. If it does, it cannot be revealed through observation. The perspective of this hypothesis is that high predictability indicates some perceptible regulative principles in the organization of the network. Putting aside any a priori hypotheses of what this regulative principle might be, we directly measure the structural consistency of a network by perturbing its adjacency matrix and observing the change of eigenvalues provided the fixed eigenvectors, similar to the well-known first-order perturbation in quantum mechanics. Although we cannot determine the maximum precision of any given link prediction algorithm, the structural consistency is a good indicator of the inherent predictability of both modeled networks and real-world networks. Surprisingly, by directly applying the first-order matrix perturbation method, we achieve more-accurate link predictions than some gracefully designed methods such as HSM (18) and SBM (25). In particular, the performance of SPM for disparate networks is very robust; i.e., it is either the best or very close to the best. In contrast, other algorithms can largely fail. For example, CN, AA, RA, and Katz indices cannot adequately manage the food web, and the HSM poorly predicts missing links in a metabolic network, which is not organized in a hierarchical way. The SPM, on the other hand, does not make any a priori assumptions about any specific organizing principles of a network, and thus its predictions are consistently more robust.
Potential applications of this work are wide and can take both theoretical and practical forms. Using structural consistency values, we can determine whether a poor prediction was caused by an inappropriate algorithm or was due to the intrinsic unpredictability of the network, and then estimate how large a space is needed to improve the algorithm. For example, the CN index does not perform well for either neural or food webs. Because the structural consistency of a food web is much larger than that of a neural web, we can infer that CN is not appropriate for a food web, while the low precision of a neural web may result from its own low predictability. Indeed, as shown in Fig. 3, the networks largely below the fitting line are those where the corresponding algorithm is not suitable to be applied. For an evolving network, the structural consistency can give a temporal estimation of whether the network becomes more elusive or not, as well as monitor the sudden changes in the evolving mechanisms (see SI Appendix, Monitor the Sudden Changes of Evolving Networks with σc, for numerical experiments). In addition, the structural perturbation method, as a straightforward extension of structural consistency, can be directly applied to determining the missing links in real-world networks. This work should be of interest to academic researchers in a variety of fields, to information technology practitioners, and to business practitioners.
Materials and Methods
Maximum Precision of Link Prediction.
If we define link predictability as the maximum precision of any link prediction algorithm, then a network is of nearly zero predictability if all nonobserved links are completely the same (e.g., a star network). For example, a vertex-transitive (20) network is of zero predictability since all of the nodes in the observed structure are identical and thus missing links are also indistinguishable from nonexistent links. For a vertex-transitive network, given any of its two nodes u and v, there is some automorphism f such that . This extremely rigid definition from automorphism-based symmetry makes virtually all real-world networks have a predictability very close to 1, since the missing links can be distinguished from nonexistent links. Because it is approximately free of graph automorphisms, link predictability approaches 1 even in ER networks (36). Thus, this rigid approach does not allow us to obtain any a useful estimation of link predictability.
Data Description.
We consider the following 10 real-world networks drawn from disparate fields: (i) Jazz (37), a collaboration network of jazz musicians consists of 198 nodes and 2742 interactions; (ii) Metabolic (38), the metabolic network of Caenorhabditis elegans; (iii) Neural (32), the neural network of C. elegans (the original network is directed and weighted; here we treat it as a simple network by ignoring the directions and weights); (iv) US Air (39), the US Air transportation network; (v) Food web (40), the food web in Florida Bay during wet season; (vi) Hamster (41), a friendship network of users on the website hamsterster.com; (vii) NetSci (42), a coauthorship network of scientists working on network theory and experiment; (viii) Yeast (43), a protein−protein interaction network in budding yeast; (ix) Email (44), a network of email interchanges between members of the University Rovira I Virgili; (x) Router (45), a symmetrized snapshot of the structure of the Internet at the level of autonomous systems; (xi) Arxiv (46), a scientific collaboration network from the arXiv’s High Energy Physics C Theory (hep-th) section; (xii) Facebook (47), a network of a small group of Facebook users; and (xiii) Enron (48), an email communication network from employees of Enron between 1999 and 2003. The more detailed information and statistical features of these networks can be found in SI Appendix, Statistical Features of Experimental Networks.
Baseline Algorithms for Link Prediction.
The link prediction problem has been a long-standing challenge in modern information science (13, 49). Its main goal is to estimate the existence likelihood of nonobserved links based on the known topology and node attributes. Link prediction has already found wide applications in interdisciplinary fields, including uncovering missing parts of social and biological networks (50–52) and recommending friends and products in online social networks and e-commerce web sites (53–55).
For comparison, we introduce four benchmark similarity indices (13). The simplest is the CN index (16) in which two nodes, x and y, have a higher connecting probability if they have more common neighbors. Two improved indices based on CN are the AA index (22) and the RA index (17, 23), both of which assign less-connected neighbors more weight. The mathematical expressions are
| [6] |
| [7] |
| [8] |
where denotes the set of neighbors of node x.
Unlike the above three local similarity indices, the Katz index (24) uses global topological information by summing over the collection of paths with exponential damping according to path lengths, i.e.,
| [9] |
which can be rewritten in the compact form, when , as
| [10] |
where I is the identity matrix, A is the adjacency matrix, and is the largest eigenvalue of A. In our experiments, we tune the parameter α to optimize the performance of the Katz index. Notice that, since α cannot be exactly zero, the Katz index cannot degenerate to the CN index. Even when α is very close to zero, the performance of the Katz index can be different from the CN index, because, under the CN index, many nonobserved links are scored the same and thus ranked in a random way (see analysis on this so-called degeneracy phenomenon in refs. 17 and 31); therefore the very slight differences contributed by the latter items in Eq. 9 may result in considerable changes in the order of nonobserved links associated with the same number of common neighbors.
We also consider two probability methods. The HSM (18) method assumes that many real-world networks are hierarchically organized and thus nodes can be divided into groups and further divided into subgroups. The SBM (25) approach is one of the most general network models. Nodes are partitioned into groups and the connecting probability of any two nodes is only determined by the groups they belong to.
Supplementary Material
Acknowledgments
We thank G. D’Agostino for helpful discussion. This work was partially supported by the National Natural Science Foundation of China (Grants 11222543, 11075031, 11205042, and 61433014), NESS Project, and CCF-Tencent Open Research Fund. L.L. acknowledges the research start-up fund of Hangzhou Normal University under Grant PE13002004039 and the EU FP7 Grant 611272 (project GROWTHCOM). T.Z. acknowledges the Program for New Century Excellent Talents in University under Grant NCET-11-0070. The work at Boston University was supported by US National Science Foundation Grants 1125290 and 0855453.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1424644112/-/DCSupplemental.
References
- 1.Barabási A-L. Scale-free networks: A decade and beyond. Science. 2009;325(5939):412–413. doi: 10.1126/science.1173299. [DOI] [PubMed] [Google Scholar]
- 2.McPherson M, Smith-Lovin L, Cook JM. Birds of a feather: Homophily in social networks. Annu Rev Sociol. 2001;27:415–444. [Google Scholar]
- 3.Currarini S, Jackson MO, Pin P. Identifying the roles of race-based choice and chance in high school friendship network formation. Proc Natl Acad Sci USA. 2010;107(11):4857–4861. doi: 10.1073/pnas.0911793107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lewis K, Gonzalez M, Kaufman J. Social selection and peer influence in an online social network. Proc Natl Acad Sci USA. 2012;109(1):68–72. doi: 10.1073/pnas.1109739109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Szabo G, Alava M, Kertész J. 2004. Clustering in complex networks. Complex Networks, Lecture Notes in Physics, eds Ben-Naim E, Frauenfelder H, Toroczkai Z (Springer, New York), Vol 650, pp 139–162.
- 6.Kossinets G, Watts DJ. Empirical analysis of an evolving social network. Science. 2006;311(5757):88–90. doi: 10.1126/science.1116869. [DOI] [PubMed] [Google Scholar]
- 7.Yin D, Hong L, Xiong X, Davison BD. 2011. Link formation analysis in microblog. Proceedings of the 34th International ACM SIGIR Conference on Research and Development in Information Retrieval (ACM Press, New York), pp 1234–1236.
- 8.Barabási A-L, Albert R. Emergence of scaling in random networks. Science. 1999;286(5439):509–512. doi: 10.1126/science.286.5439.509. [DOI] [PubMed] [Google Scholar]
- 9.Jeong H, Néda Z, Barabási A-L. Measuring preferential attachment in evolving networks. Europhys Lett. 2003;61(4):567. [Google Scholar]
- 10.Leskovec J, Backstrom L, Kumar R, Tomkins A. 2008. Microscopic evolution of social networks. Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (ACM Press, New York), pp 462–470.
- 11.Garlaschelli D, Loffredo MI. Patterns of link reciprocity in directed networks. Phys Rev Lett. 2004;93(26 Pt 1):268701. doi: 10.1103/PhysRevLett.93.268701. [DOI] [PubMed] [Google Scholar]
- 12.Marvel SA, Strogatz SH, Kleinberg JM. Energy landscape of social balance. Phys Rev Lett. 2009;103(19):198701. doi: 10.1103/PhysRevLett.103.198701. [DOI] [PubMed] [Google Scholar]
- 13.Lü L, Zhou T. Link prediction in complex networks: A survey. Physica A. 2011;390(6):1150–1170. [Google Scholar]
- 14.Wang WQ, Zhang QM, Zhou T. Evaluating network models: A likelihood analysis. Europhys Lett. 2012;98(2):28004. [Google Scholar]
- 15.Zhang QM, Lü L, Wang WQ, Zhu YX, Zhou T. Potential theory for directed networks. PLoS ONE. 2013;8(2):e55437. doi: 10.1371/journal.pone.0055437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Liben-Nowell D, Kleinberg J. The link prediction problem for social networks. J Am Soc Inf Sci Technol. 2007;58(7):1019–1031. [Google Scholar]
- 17.Zhou T, Lü L, Zhang YC. Predicting missing links via local information. Eur Phys J B. 2009;71(4):623–630. [Google Scholar]
- 18.Clauset A, Moore C, Newman MEJ. Hierarchical structure and the prediction of missing links in networks. Nature. 2008;453(7191):98–101. doi: 10.1038/nature06830. [DOI] [PubMed] [Google Scholar]
- 19.Song C, Qu Z, Blumm N, Barabási A-L. Limits of predictability in human mobility. Science. 2010;327(5968):1018–1021. doi: 10.1126/science.1177170. [DOI] [PubMed] [Google Scholar]
- 20.Godsil C, Royle G. Algebraic Graph Theory. Springer; New York: 2001. [Google Scholar]
- 21.Herlocker JL, Konstann JA, Terveen K, Riedl JT. Evaluating collaborative filtering recommender systems. ACM Trans Inf Syst. 2004;22(1):5–53. [Google Scholar]
- 22.Adamic LA, Adar E. Friends and neighbors on the web. Soc Networks. 2003;25(3):211–230. [Google Scholar]
- 23.Ou Q, Jin YD, Zhou T, Wang BH, Yin BQ. Power-law strength-degree correlation from resource-allocation dynamics on weighted networks. Phys Rev E Stat Nonlin Soft Matter Phys. 2007;75(2 Pt 1):021102. doi: 10.1103/PhysRevE.75.021102. [DOI] [PubMed] [Google Scholar]
- 24.Katz L. A new status index derived from sociometric analysis. Psychometrika. 1953;18(1):39–43. [Google Scholar]
- 25.Guimerà R, Sales-Pardo M. Missing and spurious interactions and the reconstruction of complex networks. Proc Natl Acad Sci USA. 2009;106(52):22073–22078. doi: 10.1073/pnas.0908366106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hanley JA, McNeil BJ. A method of comparing the areas under receiver operating characteristic curves derived from the same cases. Radiology. 1983;148(3):839–843. doi: 10.1148/radiology.148.3.6878708. [DOI] [PubMed] [Google Scholar]
- 27.Amaral LAN. A truer measure of our ignorance. Proc Natl Acad Sci USA. 2008;105(19):6795–6796. doi: 10.1073/pnas.0802459105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Erdös P, Rényi A. On random graphs. Pub Math Debrecen. 1959;6:290–297. [Google Scholar]
- 29.Chung F, Lu L, Vu V. Spectra of random graphs with given expected degrees. Proc Natl Acad Sci USA. 2003;100(11):6313–6318. doi: 10.1073/pnas.0937490100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Farkas IJ, Derényi I, Barabási A-L, Vicsek T. Spectra of “real-world” graphs: Beyond the semicircle law. Phys Rev E Stat Nonlin Soft Matter Phys. 2001;64(2 Pt 2):026704. doi: 10.1103/PhysRevE.64.026704. [DOI] [PubMed] [Google Scholar]
- 31.Lü L, Jin CH, Zhou T. Similarity index based on local paths for link prediction of complex networks. Phys Rev E Stat Nonlin Soft Matter Phys. 2009;80(4 Pt 2):046122. doi: 10.1103/PhysRevE.80.046122. [DOI] [PubMed] [Google Scholar]
- 32.Watts DJ, Strogatz SH. Collective dynamics of ‘small-world’ networks. Nature. 1998;393(6684):440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- 33.Ginsberg J, et al. Detecting influenza epidemics using search engine query data. Nature. 2009;457(7232):1012–1014. doi: 10.1038/nature07634. [DOI] [PubMed] [Google Scholar]
- 34.Vespignani A. Predicting the behavior of techno-social systems. Science. 2009;325(5939):425–428. doi: 10.1126/science.1171990. [DOI] [PubMed] [Google Scholar]
- 35.Goel S, Hofman JM, Lahaie S, Pennock DM, Watts DJ. Predicting consumer behavior with Web search. Proc Natl Acad Sci USA. 2010;107(41):17486–17490. doi: 10.1073/pnas.1005962107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bollobás B. Random Graphs. 2nd Ed Cambridge Univ Press; Cambridge, UK: 2001. [Google Scholar]
- 37.Gleiser P, Danon L. Community structure in Jazz. Adv Complex Syst. 2003;6(4):565–573. [Google Scholar]
- 38.Duch J, Arenas A. Community detection in complex networks using extremal optimization. Phys Rev E Stat Nonlin Soft Matter Phys. 2005;72(2 Pt 2):027104. doi: 10.1103/PhysRevE.72.027104. [DOI] [PubMed] [Google Scholar]
- 39. Batagelj V, Mrvar A (2006) Pajek datasets. Available at vlado.fmf.uni-lj.si/pub/networks/data/. Accessed May 19, 2013.
- 40.Ulanowicz RE, Bondavalli C, Egnotovich MS. 1998. Network Analysis of Trophic Dynamics in South Florida Ecosystem, FY 97: The Florida Bay Ecosystem (Chesapeake Biol Lab, Solomons, MD), Tech Rep CBL 98-123.
- 41. Kunegis J (2013) Hamsterster friendships unique network dataset – KONECT. Available at konect.uni-koblenz.de/networks/petster-friendships-hamster. Accessed June 1, 2013.
- 42.Newman MEJ. Finding community structure in networks using the eigenvectors of matrices. Phys Rev E Stat Nonlin Soft Matter Phys. 2006;74(3 Pt 2):036104. doi: 10.1103/PhysRevE.74.036104. [DOI] [PubMed] [Google Scholar]
- 43.Bu D, et al. Topological structure analysis of the protein−protein interaction network in budding yeast. Nucleic Acids Res. 2003;31(9):2443–2450. doi: 10.1093/nar/gkg340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Guimerà R, Danon L, Díaz-Guilera A, Giralt F, Arenas A. Self-similar community structure in a network of human interactions. Phys Rev E Stat Nonlin Soft Matter Phys. 2003;68(6 Pt 2):065103. doi: 10.1103/PhysRevE.68.065103. [DOI] [PubMed] [Google Scholar]
- 45.Spring N, Mahajan R, Wetherall D, Anderson T. Measuring ISP topologies with Rocketfuel. IEEE/ACM Trans Networking. 2004;12(1):2–16. [Google Scholar]
- 46.Leskovec J, Kleinberg J, Faloutsos C. Graph evolution: Densification and shrinking diameters. ACM Trans Knowledge Discovery Data. 2007;1(1):2. [Google Scholar]
- 47.Viswanath B, Mislove A, Cha M, Gummadi KP. 2009. On the evolution of user interaction in Facebook. Proceedings of the 2nd Workshop on Online Social Networks (ACM Press, New York), pp 37–42.
- 48.Klimt B, Yang Y. 2004. The Enron corpus: A new dataset for email classification research. Proceedings of the European Conference on Machine Learning (Springer, New York), pp 217−226.
- 49.Getoor L, Diehl CP. Link mining: A survey. ACM SIGKDD Explor Newsl. 2005;7(2):3–12. [Google Scholar]
- 50.Mamitsuka H. Mining from protein−protein interactions, Wiley Interdiscip Rev: Data Min Knowl Discov. 2012;2(5):400–410. [Google Scholar]
- 51.Cannistraci CV, Alanis-Lobato G, Ravasi T. From link-prediction in brain connectomes and protein interactomes to the local-community-paradigm in complex networks. Sci Rep. 2013;3:1613. doi: 10.1038/srep01613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Barzel B, Barabási A-L. Network link prediction by global silencing of indirect correlations. Nat Biotechnol. 2013;31(8):720–725. doi: 10.1038/nbt.2601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Schifanella R, Barrat A, Cattuto C, Markines B, Menczer F. 2010. Folks in folksonomies: Social link prediction from shared metadata. Proceedings of the 3rd ACM International Conference on Web Search and Data Mining (ACM Press, New York), pp 271−280.
- 54.Aiello LM, et al. Friendship prediction and homophily in social media. ACM Trans Web. 2012;6(2):9. [Google Scholar]
- 55.Lü L, et al. Recommender systems. Phys Rep. 2012;519(1):1–49. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.