Informative features of local field potential signals in primary visual cortex during natural image stimulation

Abstract

The local field potential (LFP) is of growing importance in neurophysiology as a metric of network activity and as a readout signal for use in brain-machine interfaces. However, there are uncertainties regarding the kind and visual field extent of information carried by LFP signals, as well as the specific features of the LFP signal conveying such information, especially under naturalistic conditions. To address these questions, we recorded LFP responses to natural images in V1 of awake and anesthetized macaques using Utah multielectrode arrays. First, we have shown that it is possible to identify presented natural images from the LFP responses they evoke using trained Gabor wavelet (GW) models. Because GW models were devised to explain the spiking responses of V1 cells, this finding suggests that local spiking activity and LFPs (thought to reflect primarily local synaptic activity) carry similar visual information. Second, models trained on scalar metrics, such as the evoked LFP response range, provide robust image identification, supporting the informative nature of even simple LFP features. Third, image identification is robust only for the first 300 ms following image presentation, and image information is not restricted to any of the spectral bands. This suggests that the short-latency broadband LFP response carries most information during natural scene viewing. Finally, best image identification was achieved by GW models incorporating information at the scale of ∼0.5° in size and trained using four different orientations. This suggests that during natural image viewing, LFPs carry stimulus-specific information at spatial scales corresponding to few orientation columns in macaque V1.

local field potentials (LFPs) are low-frequency voltage fluctuations (<250 Hz) recorded by extracellular microelectrodes in the brain. Although LFPs were among the earliest neural signals studied (Di et al. 1990; Kandel and Buzsáki 1997; Mitzdorf 1985; Schroeder et al. 1998), their importance as a metric of network activity has only recently reemerged. Lately, they have also proved useful for decoding activity in the brain for use in brain-machine interfaces (Andersen et al. 2004; Rickert et al. 2005). LFPs are thought to be generated by transmembrane current flow in ensembles of neurons, reflecting their input and dendritic processing (Mitzdorf 1985; Okun et al. 2010). The relationship of LFPs to local spiking activity is, however, less clear. On one hand, LFPs and local spiking activity are significantly correlated (Burns et al. 2010). In fact, part of the LFP response can be explained by linear filtering of the local spiking activity (Rasch et al. 2009); in addition, spiking is closely related to the negative phase of the LFP (Berens et al. 2008b; Donoghue et al. 1998; Fries et al. 2001), and LFPs in V1 show orientation preference and tuning similar to that of the multiunit spike activity of the local neurons (Berens et al. 2008a; Frien et al. 2000; Katzner et al. 2009). On the other hand, the two signals have also been shown to carry independent information (Belitski et al. 2008). In V1, the spiking response of single neurons to visual stimuli can be successfully explained by modeling the neuronal receptive fields (RFs) as oriented filters with one or more Gabor wavelets (GW) (Adelson and Bergen 1985; Carandini et al. 2005; Jones and Palmer 1987). We investigated whether these GW models, devised to explain the spiking responses of individual neurons, can also explain the LFP responses of V1 neurons to natural images. To this end, we trained GW models on LFP responses evoked in macaque V1 by presentation of natural images, and we attempted to identify novel images from the LFP responses they evoked on the basis of predictions from the trained model. We found that these models can identify novel images significantly above chance, suggesting that LFP and spiking activity carry similar visual information.

There are uncertainties regarding the spatial extent over which the LFP signal is integrated, with reports of LFP spatial integration ranging from about 500 μm in diameter (Katzner et al. 2009; Xing et al. 2009) to several millimeters of cortex (Kajikawa and Schroeder 2011; Kreiman et al. 2006). Furthermore, it is unknown what features of LFP signals are most informative about natural images. We addressed these questions by comparing image identification performance of GW models based on different time and frequency windows of the evoked LFP signal, and of models trained with different wavelet sizes and different numbers of orientations. We found that the short-latency broadband LFP response range carries most information during natural image viewing and that this information arises from small regions in the images, corresponding to few orientation columns in V1.

MATERIALS AND METHODS

Surgical Preparation and Recording

All experimental procedures conformed to the guidelines of the NIH and were approved by the Institutional Animal Care and Use Committee of the University of Utah. Multielectrode extracellular recordings of LFPs were made from parafoveal V1 of one awake fixating and one anesthetized (sufentanil citrate, 4–12 μg·kg⁻¹·h⁻¹) and paralyzed (vecuronium bromide, 0.1–0.3 μg·kg⁻¹·h⁻¹) male macaque monkey (Macaca fascicularis), using 96-channel (10 × 10 electrode) Utah electrode arrays. The arrays were 4 × 4 mm in size with an interelectrode distance of 0.4 mm. The electrodes were 1 mm long but were only partially inserted into the cortex; therefore, most recordings likely were from the supragranular layers of V1.

The behaving monkey was chronically implanted with the array with the use of human protocols for both the surgery and postoperative care as previously detailed (Torab et al. 2011). The animal was trained to tolerate painless head stabilization and maintain gaze fixation within a 1° window around a fixation point for a liquid reward (Davis et al. 2009). Eye movements were monitored with an infrared camera (1-kHz sampling rate; EyeLink 1000, SR Research, Mississauga, ON, Canada).

For the anesthetized monkey, surgical preparation and maintenance of anesthesia used for acute recordings were as previously detailed (Shushruth et al. 2012). A craniotomy was performed over the occipital lobe and the dura reflected. The array was inserted pneumatically, and the dura and skin were sutured back over the array to prevent tissue desiccation.

Visual stimuli were presented on a calibrated CRT monitor (ViewSonic-G90FB for the awake monkey and Sony GDM-C520K with a refresh rate of 100 Hz and mean luminance of ∼45.7 cd/m² for the anesthetized monkey) located either 34 cm (awake monkey) or 57 cm (anesthetized monkey) from the animal's eyes. The stimulus presentation was controlled by a ViSaGe system (CRS, Cambridge, UK) to ensure precise timing.

Data Acquisition and Signal Processing

Data were acquired using a 128-channel Cerebus system (Blackrock Microsystems, Salt Lake City, UT). To obtain LFPs, signals from the 96 channels on the array were bandpassed between 0.3 and 7,500 Hz and continuously recorded at a sampling rate of 30 kHz. The recorded data was further digitally low-pass filtered below 250 Hz to isolate the LFPs and downsampled to 2,000 Hz. All LFP analyses were performed on this downsampled version.

Multiunit activity (MUA) was derived by high-pass filtering the broadband response recorded from the array, as described by Xing et al. (2012). In the anesthetized monkey, the MUA data was obtained by high-pass filtering the raw signal above 1 kHz and downsampling to 5 kHz, resulting in 0.2-ms time bins. The array in the awake monkey was a long-term (>1 yr) chronic implant, and hence, as commonly seen with chronic implants, there was a reduction in the ability to isolate spiking activity; for this reason, filtering was performed above 250 Hz. The filtered signal was full-wave rectified. MUA was characterized as the fraction of time bins whose activity was 3 SD above the activity during the interstimulus interval. MUA in the 40- to 300-ms time window following image presentation was used as the scalar image response; the rest of the modeling was performed as for the LFP signals. Note that LFP responses were derived from the raw voltage responses after low-pass filtering below 250 Hz, so the MUA and LFP responses are different measures of neural activity.

For spectral analysis, power at various spectral bands of the LFP signal was calculated with multitaper methods (Bokil et al. 2010) using the Chronux Matlab toolbox (www.chronux.org). Because we considered signals 0.5 s long, we set the number of orthogonal Slepian tapers to 3, which resulted in a half-bandwidth of 4 Hz.

Visual Stimuli

RF mapping.

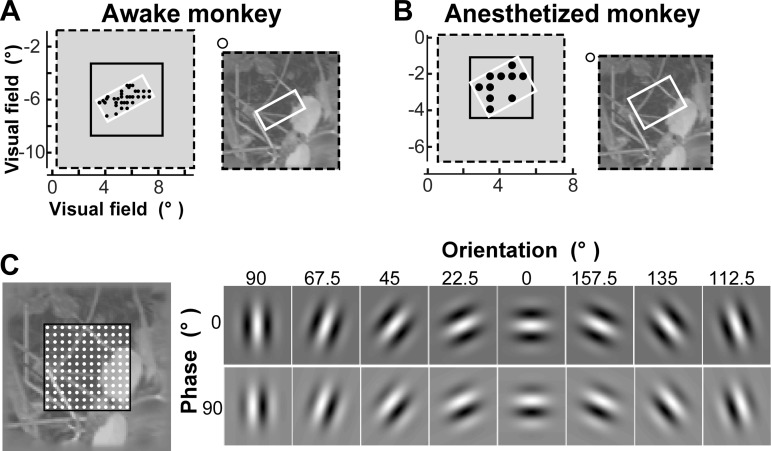
The retinotopic locations of the RFs on the array were mapped using sparse noise stimuli and analyzing the evoked LFPs. Specifically, small square dark or bright stimuli (0.1°–0.3° side) were presented for 100–300 ms on a gray background at locations defined by a rectangular grid. The stimulus location that evoked the largest LFP response (measured as the area under the average LFP response trace, i.e., the integral of the LFP trace) on an electrode was considered the center of the RF of that electrode. The retinotopic locations of the RFs across the array are shown as black dots in Fig. 1, A and B, left.

Fig. 1.

Visual stimuli and the Gabor wavelet (GW) model. A and B: an example natural image in the awake monkey (A) and the anesthetized monkey (B). Left, visual field locations of the presented natural image (black dashed box), recording array (white box), and image portion used for model training (solid black box). Black dots indicate the center of the receptive field (RF) mapped at each electrode (for many electrodes the RF locations overlapped, and this is indicated by larger dots). Right, each presented natural image (dashed black box) was overlaid onto the RF map under the array (white box). The visual field locations of the image (black dashed box) and the array (white box) are shown in each respective left panel. Open circle indicates the fixation point (awake monkey) or location of the fovea (anesthetized monkey). C: GW model. Left, grid scheme used for model training. Gabor wavelets were computed at each grid point (white dots). The visual field location of the region outlined in black is indicated by the solid black box shown in A and B, left. Different grid sizes were used for wavelets of different sizes, i.e., denser grids were used for smaller sizes. Right, complete set of Gabor wavelet orientations and phases used in the model. At each grid position, wavelets occurred at 8 different orientations and 2 phases.

Natural images.

We chose our stimulus images from the van Hateren natural image database of 4,000 images (van Hateren and van der Schaaf 1998) after cropping the images to their central 768 × 768 pixels. From this database we selected 200 images. To ensure that these images represented a broad range of orientation power spectra, they were selected as follows. We defined orientation power as

$${\text{P}}_i={\displaystyle \underset{{\theta }_i}{\overset{{\theta }_{i+1}}{\int }}F\left(r,\theta \right)d}\theta ,$$

where F(r, θ) is the Fourier transform of the cropped image expressed in polar coordinates, and θ₁, . . . , θ₂₀ are the limits of 20 orientation bins that we used. Then P₁, . . . , P₂₀ are the 20 elements of the orientation power spectrum. We also created a luminance histogram by using g₁, . . . , g₂₀ as the limits of 20 luminance bins. Then H₁, . . . , H₂₀ are the 20 elements of the luminance histogram. We created a feature vector for each of the 4,000 images by concatenating P₁, . . . , P₂₀ and H₁, . . . , H₂₀. We then separated the cropped images into 10 primary clusters by using the k-means algorithm (Duda et al. 2000) in this feature space. We chose 10 clusters to ensure that even the smallest clusters had a sufficient number of visually discernable images. Twenty images were chosen from each of the 10 primary clusters by further dividing the images in each cluster into 5 subclusters (again using the k-means algorithm) and randomly choosing 4 images from each subcluster. The image set (200 images) was equalized for mean luminance and root mean square (RMS) contrast. To minimize stimulation of the more distant modulatory surround region of V1 neurons (Angelucci et al. 2002), the images were further cropped to their central 192 × 192-pixel square and embedded in a background having the same mean luminance as that of the processed image set (Fig. 1, A and B). Our reason for further cropping the images was motivated by a parallel study in which we are investigating the GW models' ability to identify images only on the basis of LFP signals evoked by stimulation of the far surround (the surround region beyond that stimulated in this study). The edges of the image region (16 pixels wide) were linearly blended into the background. Of these 200 images, 100 (2 from each subcluster; i.e., 10 images from each cluster) were used as stimuli for the experiments. The remaining 100 images (i.e., the remaining 2 images from each subcluster) were used for model testing as explained below (see The Gabor Wavelet Model).

Images were presented on a computer monitor for 500 ms, followed by a 500-ms interstimulus interval, in pseudorandom order. Each image was presented 10–30 times in the awake monkey and 20 times in the anesthetized monkey. The image sides subtended a visual angle of 10.4° (awake monkey) or 7° (anesthetized monkey) and overlay the retinotopic position of the array (Fig. 1, A and B). For the awake monkey, image presentation began 500 ms after fixation was acquired and continued while the monkey maintained fixation within a 1° window around the fixation point. Image presentation was terminated if fixation was broken. For analysis we only used recording data acquired while the monkey maintained fixation for the entire 500 ms of image presentation. LFP responses to all images were recorded over the course of five separate sessions for the awake monkey and in a single acute session in the anesthetized monkey.

The Gabor Wavelet Model

Model architecture and training.

We used stimulus-evoked LFP responses to 100 images presented to the monkeys to train Gabor wavelet pyramid (GW) models (Jones and Palmer 1987; Kay et al. 2008; Lee 1996) (Fig. 1C). The models were applied to a 100 × 100-pixel square field of view (indicated as a solid black box in Fig. 1, A–C) of each presented image, corresponding to a visual field extent of 5.4° × 5.4° (awake monkey) or 3.6° × 3.6° (anesthetized monkey). Gabor wavelets were positioned on a k × k grid (k = 24, 12, 4, 2, and 1 grid positions for the awake monkey, and k = 16, 8, 2, and 1 for the anesthetized monkey). This corresponded, respectively, to wavelet sizes of 0.225°, 0.45°, 1.3°, 2.7°, and 5.4° (awake monkey) or 0.225°, 0.45°, 1.8°, and 3.6° (anesthetized monkey). At each grid position, wavelets occurred at two orthogonal phases and up to eight orientations, and for each wavelet the standard deviation of the underlying Gaussian equaled half its wavelength (Fig. 1C, right).

We trained the GW model to predict different features of the LFP signal as reported in results. Here we describe how model training was performed for one such feature, i.e., the signal range, defined as the difference between the maximum and minimum of the average LFP response trace during the 40- to 300-ms time window following image presentation (Fig. 2C). Each image was projected onto the set of Gabor wavelets, and the projections for the two orthogonal phases were squared, summed, and square rooted at each grid point (to obtain a measure of contrast energy). These set of values were then used as inputs to a linear RF model, which estimated the LFP signal range for each of the 96 electrodes on the array.

Fig. 2.

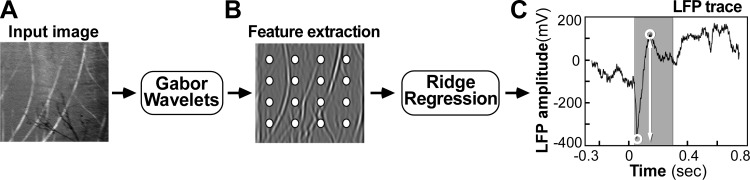
Model training. From the input image (A), a set of features was extracted using Gabor wavelets (B). A ridge regression model was then trained to predict the local field potential (LFP) response range (C) from this set of features. The shaded area in C marks the 40- to 300-ms time window following image presentation. The range of the LFP signal (predicted by the model) is marked by a white double arrow. For simplicity, in C we show the average LFP trace for one image at one electrode. In reality, one such model was trained for each electrode separately.

The parameters of the linear RF model were learned by using a ridge regression model as follows. Let n be the number of images and m be the number of responses from the GW model for each input image. Each LFP feature (here in particular the LFP signal range) was modeled as

$$y=Xw,$$

where X denotes the set of input responses (n × m), y is the LFP feature (here the range) averaged over trials for a single electrode (n × 1), and w (m × 1) is the weight vector to be learned. The ridge regression model minimizes the following loss function to find w:

$$L(w)=\frac{1}{2}\hspace{0.17em}\Vert y-Xw{\Vert }_2^2+\lambda \phi (w),$$

where φ(w) is a regularizer function that reduces overfitting and λ is the weight of regularizer in the optimization problem. In our model, φ(w) is the l₂ norm of the weight vector w. The parameter λ was tuned by cross-validation on a subset of 10% of the data that was held out from the training set (λ = 0.8 in the case of the signal range but is tuned for each LFP feature separately). We checked the performance (see Model performance metrics) on the validation set for different values of λ and selected the value with the best generalization performance, i.e., the performance on the held-out data. We emphasize that neither the training set nor the held-out set were used at test time to compute the identification performance and that the test set consisted of novel images. The model training is illustrated in Fig. 2.

We also compared the GW model with a pixel model, in which we used single pixel intensities from the center location of where the corresponding wavelets would be computed as the input responses in the GW model. The remainder of the methodology for the pixel model was as for the GW model.

Model performance metrics.

COEFFICIENT OF DETERMINATION.

The encoding efficiency of a model for responses recorded by each electrode in the array is dependent on multiple factors. One factor is the signal-to-noise ratio for the specific electrode. More importantly, because each electrode samples only the part of the image overlying the RFs of its recorded neurons, given the small number (i.e., 99) of images in our training set for any given iteration, there will be large variability across the electrodes in the diversity of images they have sampled relative to the space of all possible natural images. Thus the ability to predict novel stimuli using a particular electrode reflects both its signal-to-noise ratio and the diversity of the images that the RFs of its recorded neurons were able to sample.

To measure the performance of the model on each electrode, we computed the coefficients of determination (R² coefficients). These coefficients reflect the proportion of the variability in the data that can be captured by our model:

$$R^2=1-\frac{{\text{Var}}_{\text{err}}}{{\text{Var}}_{\text{data}}},$$

where Var_err denotes the mean squared error in the model and Var_data is the variance of the input data. A higher R² value signifies a better encoding model, with the caveat of inflated values from overfitting. We used the average R² across all electrodes on the 10% of the data held out from training to tune the parameter λ in the least-square minimization. This enabled us to make our model robust to over fitting without utilizing any of the data that would be used for testing identification performance. Moreover, note that overfitting would negatively impact the model performance during testing because our testing image set was different from the training image set.

IMAGE IDENTIFICATION.

To assess model performance, we used the model to identify novel images on the basis of LFP responses. Image identification was performed using the following strategy. First, 1 of the 100 images that were presented to the monkeys (for which we had recorded LFP responses) was removed (the “flag” image) and the remaining 99 images were used for model training on a specific LFP feature. These 99 images constituted the training image set. The model was then used to predict the specific LFP feature used for model training on each of the 96 electrodes for a different set of images, here termed the test image set. We used test image sets of different sizes, i.e., 2, 5, or 10 images, that consisted of the flag image plus 1, 4, or 9 novel images, respectively, drawn from the 100 images that were initially removed from the original 200 images selected from the Van Hateren database as described above (see Natural images). Therefore, the images used for model training and those used for model testing were composed of different images but were, however, similar with respect to their distributions of orientation power spectrum, luminance, and contrast, because they were drawn from the same image clusters and subclusters. This ensured that there was no bias toward identification of the flag image. The Euclidean distances between the experimentally recorded LFP feature of the flag image and the model-predicted LFP feature for all test images in a set were computed. The model was considered to have correctly identified the flag image if this distance was smallest for the flag image compared with the other images in the test set. This procedure enabled us to evaluate model predictions in the space of possible responses that can be elicited by natural images. We repeated this process 100 times by removing a different image from the training image set each time. Furthermore, for each of the 100 images removed from the training set, we used 85 different test sets (i.e., consisting of different images taken from the pool of 100 novel images) for each test set size (2, 5, or 10 images, i.e., 85 × 3 test sets for each removed image) to compute the model performance as a function of the test set size.

Correlation Analysis

To obtain a model-free coarse estimate of the spatial spread of LFP signals, we calculated the correlation of the broadband LFP signals as a function of electrode separation. Pairwise correlation coefficients were calculated for each electrode pair for each image using the mean LFP response to the images (between 40 and 300 ms after image presentation). The equivalent time window preceding the image presentation was used to calculate the baseline correlation. The electrode pairs were binned on the basis of their separation, and for each image the mean correlation was calculated for each bin.

RESULTS

We recorded LFP responses to 100 natural images from V1 of one awake fixating and one anesthetized macaque monkey using Utah multielectrode arrays. The images were selected from a larger database (van Hateren and van der Schaaf 1998) using an approach that ensured they encompassed a broad range of orientation power spectra (see materials and methods). The retinotopic locations of the RFs corresponding to the electrodes on the array were first mapped using sparse noise stimuli. The arrays encompassed a visual field region ∼3° × 4° (awake monkey) or 3.5° × 3.5° (anesthetized monkey) in size and were centered at ∼7.5° and 5.5° eccentricity, respectively (Fig. 1, A and B, left). The natural images presented to the monkeys were overlaid onto the visual field region encompassed by the array but extended beyond it [up to 3° (awake monkey) or 2.5° (anesthetized monkey) from the center of the RFs located at the edge of the array] (Fig. 1, A and B, right). Images were 10.4° × 10.4° (awake monkey) or 7° × 7° (anesthetized monkey) in size (Fig. 1, A and B, left). We used the imaged-evoked LFP responses to train GW models, which describe tuning along the dimensions of space, orientation, and spatial frequency (Fig. 1C). GW models were trained by projecting the images onto Gabor wavelets and learning the parameters of the model by ridge regression (see materials and methods and Fig. 2). We then validated these models by predicting LFP responses to novel images (i.e., not used for model training) and attempting to identify the images on the basis of the model-predicted LFP traces.

GW Models Provide Reliable Predictions of LFP Response Range

The reliability of the model-predicted LFP responses to natural images was quantified as the model's ability to correctly associate a given LFP response to the image that evoked it among a set of images. We initially used the range of LFP response (maximum minus minimum), henceforth termed “response range,” elicited by the image in the 40- to 300-ms postpresentation time window as our measure of LFP response (Fig. 2C). We surmised that signals in this time window would be physiologically relevant because the average fixation duration for macaques freely viewing natural scenes is 350 ms (Vinje and Gallant 2000). To assess model performance, we used the model for novel image identification, based on LFP responses, as detailed in materials and methods (see Image identification). Model performance was expressed as a percentage of novel images that were correctly identified as a function of test set size.

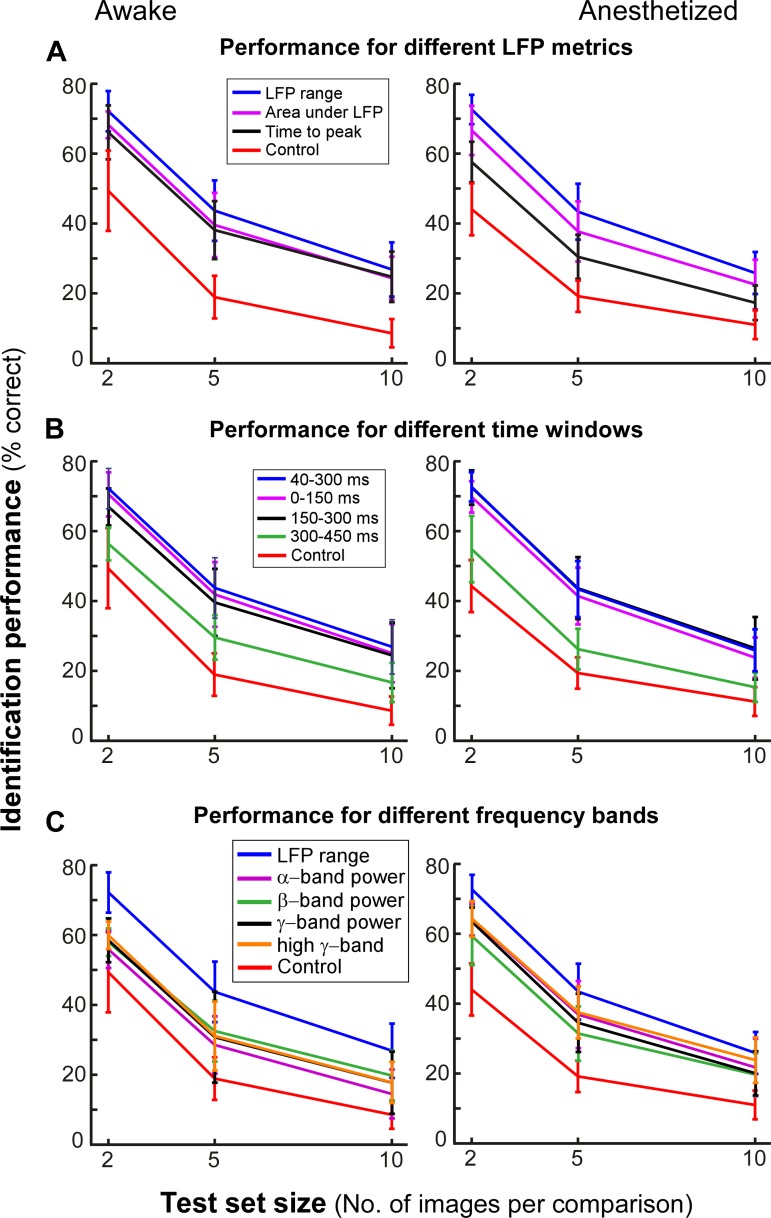
Figure 3A shows the identification performance of the GW model for the awake (left) and anesthetized monkeys (right). For both monkeys, 72% of the images were identified correctly by the GW model when the test set consisted of 2 images. As set size increased 5-fold from 2 to 10 images, performance declined to about 26% but remained well above chance (10%) as well as above the performance of a control GW model trained on baseline LFP responses (40–300 ms before image onset). For comparison we also used a “pixel model,” which is based on the pixel intensity values at the same grid positions as the wavelets in the GW model (see materials and methods). Whereas this model also performed above chance, the GW model significantly outperformed it (P < 10⁻¹¹, for all conditions in both monkeys on paired Wilcoxon signed rank test with Bonferroni correction; Table 1).

Fig. 3.

Image identification performance of the GW model trained on stimulus-evoked LFP or multiunit activity (MUA). Identification performance of the GW model was compared with the performances of a comparison pixel model and a control GW model trained on LFP data (A) or MUA data (B). Model performance was based on data from awake monkey (left) and anesthetized monkey (right). Blue curves represent identification performance of the GW model trained to predict LFP (A) or MUA (B) response range and computed with Gabor wavelets of 0.45° in size at 8 different orientations. Green curves represent identification performance for the pixel model. In both models the same k × k grid was used (k = 12 for awake monkey and 8 for anesthetized monkey). Red curves represent performance of control GW model trained using data in the 40- to 300-ms time window before image onset. Error bars represent 1 SD from average performance.

Table 1.

P values of the paired Wilcoxon signed rank test comparing the GW model with the pixel model (LFP data)

Test Set Size, No. of Images	Awake Monkey	Anesthetized Monkey
2	1.15 × 10−15	2.44 × 10−15
5	4.13 × 10−14	1.2 × 10−15
10	8.59 × 10−12	2.66 × 10−15

All data in Tables 1–9 are P values in awake and anesthetized monkey as indicated.

GW, Gabor wavelet; LFP, local field potential.

We also assessed the performance of the GW model trained on MUA extracted from the same data set in the same time windows as for the LFP signal analysis (see materials and methods). As expected, images could also be reliably identified on the basis of MUA (Fig. 3B and Table 2).

Table 2.

P values of the paired Wilcoxon signed rank test comparing the GW model with the pixel model (MUA data)

Test Set Size, No. of Images	Awake Monkey	Anesthetized Monkey
2	2.28 × 10−7	1.42 × 10−15
5	1.70 × 10−12	1.66 × 10−15
10	4.80 × 10−15	1.22 × 10−15

MUA, multiunit activity.

The good performance of the GW model indicates that this model captures important characteristics of the LFP responses of V1 neurons to natural images. Higher performance of the GW model compared with the pixel model indicates that identification improves substantially when orientation and spatial frequency tuning are included in the model.

Informative Features of LFP Signals in the Time and Frequency Domains

Because of the complexity of sources contributing to LFP signals, it is unclear how relevant information about a natural image evolves over time and which spectral bands carry this information. Therefore, we investigated the image identification performance of the model based on data from different time windows and different frequency bands of the LFP response.

Time course.

In the previous section we used a simple metric, the range of the LFP signal, for assessing the model performance. To determine whether this feature of LFP signals provides the best image discriminability, we compared the performances of models trained using two other biologically motivated scalar metrics: 1) the area under the LFP curve during the 40- to 300-ms time window following image presentation and 2) the time interval from image onset to first peak. Importantly, the model was trained and tested on the same metric. Figure 4A compares identification performance of the GW model for each of these LFP metrics in the awake (left) and anesthetized monkeys (right). Although performance was well above control for each metric, the LFP response range significantly outperformed the other two (P < 10⁻¹⁰ in the anesthetized monkey and P < 10⁻⁵ for all comparisons except one for the awake monkey; paired Wilcoxon signed rank test with Bonferroni correction; Table 3).

Fig. 4.

Informative features of the LFP in the time and frequency domains. A: GW model performance for different predicted LFP metrics (indicated by different colored curves per key). For all predicted features, the Gabor wavelets were computed at size 0.45° and at 8 different orientations. B: GW model performance for different time windows. C: model performance for different frequency bands. Other conventions are as described for Fig. 3.

Table 3.

P values of the paired Wilcoxon signed rank test comparing the model using range as the metric with the model using other metrics (LFP data)

	Area Under LFP Curve		Time to Peak
Test Set Size, No. of Images	Awake	Anesthetized	Awake	Anesthetized
2	1.08 × 10−10	5.94 × 10−12	1.13 × 10−8	2.62 × 10−15
5	3.93 × 10−10	1.01 × 10−12	5.88 × 10−7	1.29 × 10−15
10	2.58 × 10−6	5.89 × 10−11	0.0202	1.64 × 10−15

We next used the response range metric to assess the model identification performance based on LFP responses in 150-ms time windows following image onset (Fig. 4B). Performance was high in both the 0- to 150-ms and 150- to 300-ms time windows, and nearly equivalent to peak performance obtained by considering the response in the 40- to 300-ms window. In contrast, performance dropped when data from the 300- to 450-ms time window were used (P < 10⁻¹², Wilcoxon signed rank test with Bonferroni correction; Table 4), indicating that in V1 relevant information about natural scenes is contained in the first 300 ms of the LFP response.

Table 4.

P values of the paired Wilcoxon signed rank test comparing the model using a 300- to 450-ms time window with the model using other time windows (LFP data)

	0–150 ms		150–300 ms
Test Set Size, No. of Images	Awake	Anesthetized	Awake	Anesthetized
2	1.36 × 10−15	3.79 × 10−14	1.40 × 10−15	1.65 × 10−14
5	2.22 × 10−15	1.18 × 10−15	4.42 × 10−14	1.14 × 10−15
10	3.74 × 10−15	1.17 × 10−15	4.83 × 10−13	4.21 × 10−15

Frequency bands.

Our modeling approach also enabled us to investigate the discriminable information about natural images that is present in the various spectral bands of the LFP response. We extracted the mean power in the alpha (8–12 Hz), beta (13–30 Hz), gamma (31–50 Hz), and high-gamma (51–80 Hz) bands from the LFP responses using a multitaper approach (see materials and methods). Image identification performance of models trained on data from each spectral band was significantly below that of the model trained on the response range (P < 10⁻¹² in the awake monkey and P < 10⁻³ in the anesthetized monkey; Wilcoxon signed rank test), but it was still above that of control performance (see Fig. 4C and Table 5). Furthermore, identification performance was largely similar for models trained on different spectral bands, suggesting that discriminable information about natural images is not specific to any oscillatory component but is a property of the broadband LFP response elicited by the images.

Table 5.

P values of the paired Wilcoxon signed rank test comparing the model using range as the metric with the model using different spectral bands (LFP data)

	Power in Alpha Band		Power in Beta Band		Power in Gamma Band		Power in High-Gamma Band
Test Set Size, No. of Images	Awake	Anesthetized	Awake	Anesthetized	Awake	Anesthetized	Awake	Anesthetized
2	1.80 × 10−15	1.17 × 10−13	2.44 × 10−15	1.34 × 10−14	1.66 × 10−15	3.82 × 10−15	1.22 × 10−15	1.51 × 10−13
5	2.57 × 10−15	3.11 × 10−9	7.05 × 10−15	1.62 × 10−14	5.71 × 10−15	3.01 × 10−12	1.62 × 10−14	3.22 × 10−9
10	1.31 × 10−15	1.50 × 10−10	4.60 × 10−13	3.65 × 10−14	3.04 × 10−13	5.55 × 10−12	1.25 × 10−13	1.11 × 10−4

Spatial Spread of LFP Signals

The extent in the visual field over which LFP signals carry information about a natural stimulus is unknown. Two factors contribute to the visual spread of LFP signals, the electrical spread of the signal in the cortical tissue and the spread due to long-range connections within V1 (horizontal) and from higher areas to V1 (feedback) (Angelucci and Bressloff 2006). There are contradicting reports on the spatial extent of the cortical region that generates LFP signals. These reports range from about 500-μm diameter (Katzner et al. 2009; Xing et al. 2009), corresponding to about 0.5° diameter of visual space at the foveal eccentricities of our recordings (note that in Fig. 1 each 4-mm-wide array covers about 4° of visual space) to several millimeters (Kajikawa and Schroeder 2011; Kreiman et al. 2006). The contribution of long-range connectivity to the visual spread of LFP signals has not been extensively investigated, but we recently found that LFP signals in V1 can be recorded at large distances (>10° at parafoveal eccentricities) from the stimulated regions (Shushruth et al. 2011), suggesting these signals are carried by long-range connectivity.

To address the question of the visual spread of the LFP signal, we examined the model performance for GW features computed at different spatial scales. For example, if LFP signals integrate information at a local scale, e.g., 0.5°, we would expect the best model performance for Gabor wavelets of similar size. This is because, to maximize decoding, the spatial size of the filter has to match the spatial size at which information is being represented. A GW of smaller size, therefore, would be suboptimal, because it would carry less information about the LFP than a 0.5° GW. On the other hand, a GW of larger size, while pooling information from a larger image area, would not necessarily carry the same information encoded by the LFP; this unrelated information would thus degrade the model performance.

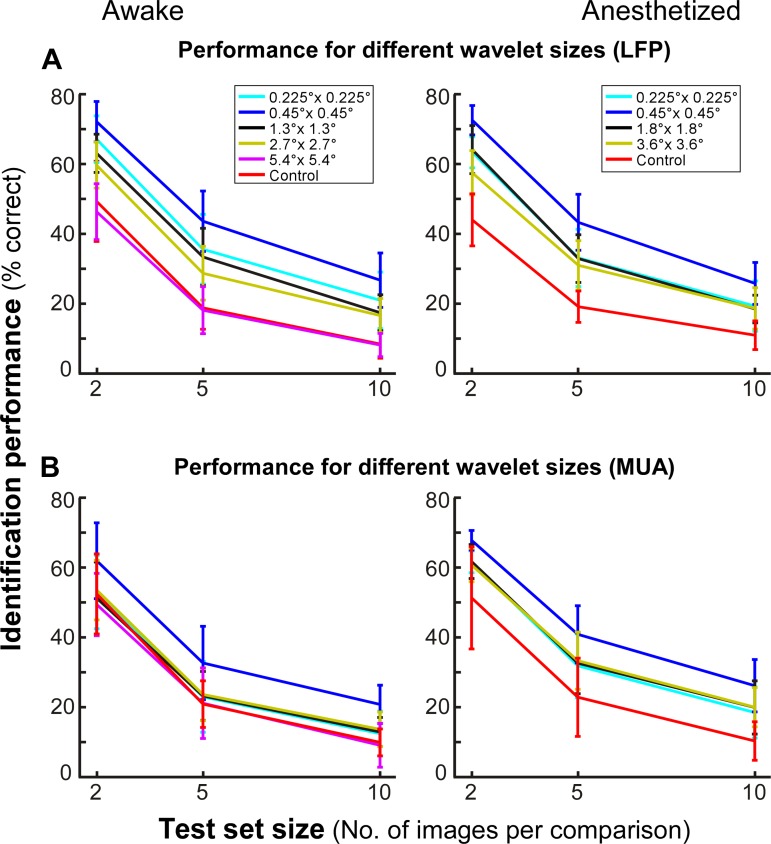
Figure 5A shows image identification performance of the GW model for different size wavelets used to model the LFP range. Although the model performed above chance for all but the largest wavelet sizes (5.4°), performance was significantly higher at 0.45° (P < 10⁻⁹, Wilcoxon signed rank test with Bonferroni correction; Table 6). Note that identification performance is not a monotonic function of wavelet size, since model performance decreased for wavelet sizes <0.45°; this suggests that the improvement in performance with decreasing wavelet size was not simply due to the increased number of parameters in the model and that coarse sampling of the image by the wavelets is not a limitation in our model. Similar results were observed for both the awake and anesthetized monkeys, suggesting that the LFP carries stimulus-specific information at these spatial scales. These measures of LFP spread are in agreement with those previously reported in V1 of anesthetized animals presented with artificial stimuli (Berens et al. 2008a; Katzner et al. 2009; Xing et al. 2009).

Fig. 5.

Spatial spread of LFP and MUA signals. A: performance of GW model trained on LFP as a function of wavelet size. B: performance of model trained on MUA as a function of wavelet size (according to key in A). At each size, wavelets were computed at 8 different orientations. Other conventions are as described for Fig. 3.

Table 6.

P values of the paired Wilcoxon signed rank test comparing the model using 0.45° wavelet size with the model using larger or smaller wavelet sizes (LFP data)

	0.225° Wavelet Size		1.3–1.8° Wavelet Size		2.7° Wavelet Size	3.6° Wavelet Size	5.4° Wavelet Size
Test Set Size, No. of Images	Awake	Anesthetized	Awake	Anesthetized	Awake	Anesthetized	Awake
2	2.22 × 10−12	5.62 × 10−15	2.24 × 10−13	9.27 × 10−12	1.32 × 10−14	5.73 × 10−15	1.20 × 10−15
5	3.94 × 10−10	7.46 × 10−14	6.03 × 10−10	4.99 × 10−13	1.23 × 10−13	7.25 × 10−12	1.20 × 10−15
10	3.00 × 10−12	5.60 × 10−12	7.34 × 10−12	1.99 × 10−13	1.48 × 10−11	8.39 × 10−13	1.49 × 10−15

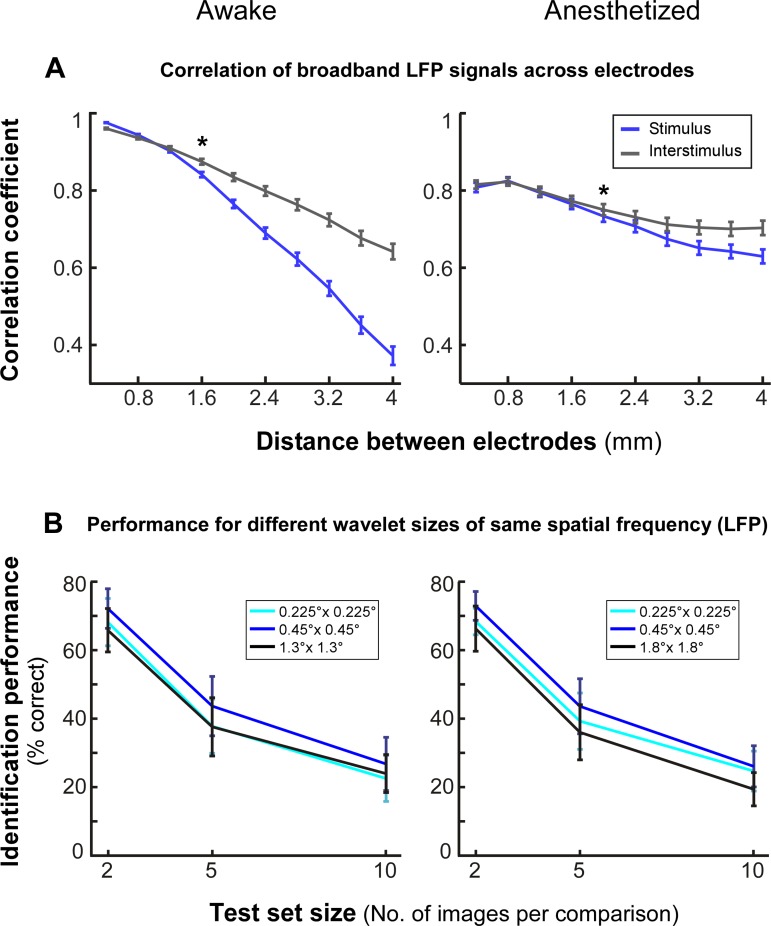
Because the Gabor model samples space in a quantized manner, as further support for the model results as well as to obtain an upper-bound model-independent measure of the spatial spread of the LFP, we performed the following analysis. We measured the correlation between the broadband LFP signals as a function of recording electrode distance during natural image stimulation (see materials and methods) and compared this with the signal correlation measured for the same electrodes during the preceding interstimulus interval. Stimulation with natural images reduced the correlation compared with the unstimulated condition (Fig. 6A). In the awake monkey, this reduction began at distances >1.2 mm of electrode separation and was statistically significant at 1.6-mm separation (P < 10⁻³, paired t-test); in the anesthetized monkey, reduced correlation began at electrode separations >1.6 mm and was statistically significant at 2-mm separation (P < 0.05). At 7.5° (awake monkey) and 5.5° (anesthetized monkey) eccentricity, these cortical distances correspond to 1–1.4° (awake monkey) and 1.1–1.3° (anesthetized monkey) of visual space (using magnification factor values from Van Essen et al. 1984). This coarse, model-free measure sets an upper bound of ∼1–1.4° for the spread of LFP signals between two electrodes.

Fig. 6.

Spatial spread of LFP signals: control analyses. A: correlation of LFP responses as a function of electrode separation. The mean correlation across the 100 images presented is shown for electrode pairs binned at multiples of 0.4-mm separation calculated after image presentation (blue) or during the preceding interstimulus interval (gray). *P < 0.05, indicating statistical significance. B: performance of model trained on LFP for different wavelet envelope sizes but matched for spatial frequency.

Finally, because in our model the size of the Gabor envelope determines the spatial frequency of the filter, to disambiguate the effect of size from that of spatial frequency, we performed a control analysis equating the spatial frequency of the 0.45° filter with the filter of the next lower (0.225°) or next higher [1.3° (awake monkey) and 1.8° (anesthetized monkey)] size. After we controlled for spatial frequency, the best model performance was still obtained for 0.45° wavelet size (Fig. 6B).

We also performed the same analysis of spatial spread for MUA in the same time window as for the LFP signal. The inferred spread of MUA was very similar to that of LFP (Fig. 5B and Table 7). This result is consistent with previous studies that used artificial stimuli (Xing et al. 2009).

Table 7.

P values of the paired Wilcoxon signed rank test comparing the model using 0.45° wavelet size with the model using larger or smaller wavelet sizes (MUA data)

	0.225° Wavelet Size		1.3–1.8° Wavelet Size		2.7° Wavelet Size	3.6° Wavelet Size	5.4° Wavelet Size
Test Set Size, No. of Images	Awake	Anesthetized	Awake	Anesthetized	Awake	Anesthetized	Awake
2	1.26 × 10−9	4.40 × 10−15	1.29 × 10−8	2.59 × 10−12	3.41 × 10−7	5.57 × 10−14	2.42 × 10−11
5	2.01 × 10−8	1.70 × 10−12	2.24 × 10−8	3.67 × 10−11	1.93 × 10−8	8.27 × 10−9	1.62 × 10−9
10	4.27 × 10−13	9.13 × 10−13	1.75 × 10−12	4.09 × 10−9	3.65 × 10−11	5.90 × 10−9	4.85 × 10−14

Orientation Tuning of LFP Signals

The data showing the effects of wavelet size on model performance suggested that the LFP integrates information over a cortical area larger than a single orientation domain. Therefore, we examined how model performance was affected by varying the number of orientations of wavelets in the GW model. Figure 7A shows image identification performance when different numbers of wavelet orientations were included in the GW model. Although even a Gaussian scale space, which has no directionality (0 orientations), performed better than the control, there was a large increase in performance when a GW model with two orientations (horizontal and vertical) was used. Increasing the number of orientations in the GW model to four (0°, 45°, 90°, and 135°) provided an additional modest, but significant, increase in performance (P ≤ 0.006 in the awake monkey, P < 10⁻⁹ in the anesthetized monkey; paired Wilcoxon signed rank test with Bonferroni correction; Table 8). Inclusion of eight orientations (0°, 22.5°, 45°, 67.5°, 90°, 112.5°, 135°, and 157.5°), instead, provided no additional improvement in performance (no rejection of null hypothesis at the 0.017 significance level; Table 8). Thus the LFP seems to integrate signals at spatial scales slightly larger than a single orientation column in macaque V1, but smaller than an orientation hypercolumn (see discussion).

Fig. 7.

Orientation tuning of LFP and MUA signals. Image identification performance of GW model trained on LFP (A) or MUA (B) is shown as a function of number of orientations (according to key in A). At all orientations, wavelets were computed at 0.45° size. 0 orientations: Gaussian filter. Other conventions are as described in Fig. 3.

Table 8.

P values of the paired Wilcoxon signed rank test comparing the model using 4 orientations with the model using larger or smaller numbers of orientations (LFP data)

	8 Orientations		2 Orientations		0 Orientations
Test Set Size, No. of Images	Awake	Anesthetized	Awake	Anesthetized	Awake	Anesthetized
2	0.0105	Not rejected (0.9255)	5.51 × 10−8	8.16 × 10−13	2.85 × 10−15	1.09 × 10−14
5	0.0045	Not rejected (0.6095)	0.0061	1.34 × 10−12	3.54 × 10−14	2.1 × 10−15
10	Not rejected (0.2821)	0.0133	Not rejected (0.0608)	3.98 × 10−10	8.37 × 10−14	1.25 × 10−15

A similar analysis performed on MUA, instead, revealed a slight but significant (P < 10⁻³; Table 9) increase in performance for the model including eight orientations compared with the model including four orientations, but more so in the anesthetized monkey, suggesting a more local scale of integration for MUA compared with LFP (Fig. 7B). The MUA analysis in the awake monkey yielded a less consistent increase in performance for the eight-orientation model. This may be due to the weaker MUA signals recorded in this monkey after years of array implantation (see materials and methods) or to a slightly larger area of integration for MUA because of the more peripheral eccentricity (7.5°) of the recordings in this monkey compared with that in the anesthetized monkey (5.5°).

Table 9.

P values of the paired Wilcoxon signed rank test comparing the model using 4 orientations with the model using larger or smaller numbers of orientations (MUA data)

	8 Orientations		2 Orientations		0 Orientations
Test Set Size, No. of Images	Awake	Anesthetized	Awake	Anesthetized	Awake	Anesthetized
2	Not rejected (0.5805)	8.22 × 10−4	Not rejected (0.3707)	1.26 × 10−11	6.51 × 10−9	3.77 × 10−14
5	7.79 × 10−4	5.90 × 10−7	Not rejected (0.6480)	1.85 × 10−4	6.77 × 10−13	2.62 × 10−13
10	4.73 × 10−5	1.75 × 10−9	Not rejected (0.3116)	Not rejected (0.8067)	1.43 × 10−15	6.39 × 10−10

DISCUSSION

We have shown that it is possible to predict LFP responses evoked by natural images using encoding models of V1 RFs devised to account for the spiking response of single V1 neurons, such as the GW models. These models can predict multiple features of the stimulus-evoked LFP signal, with the signal range providing the most reliable predictions. Furthermore, the best performance in image identification based on predicted LFP signals was obtained for a model with Gabor wavelets of about 0.5° size and 4 orientations. This suggests that the LFP signal during natural image viewing carries specific information about small image regions, corresponding to a cortical region about 500 μm in diameter, i.e., larger than a single orientation column but smaller than an orientation hypercolumn (i.e., a full cycle of orientation columns).

LFPs Can Be Predicted by Spiking RF Models in V1

LFPs are thought to reflect local current sources and sinks whose largest contribution arises from synaptic activity and subthreshold membrane oscillations (Mitzdorf 1985; Okun et al. 2010). Synaptic activity at a cortical region is not just influenced by narrowly spreading thalamic inputs (Angelucci and Sainsbury 2006) but can arise from considerable distances from the recording electrode via long-range intra-V1 horizontal connections and feedback connections from extrastriate cortex (Angelucci et al. 2002). Because these long-range connections only elicit subthreshold responses, thus modulating rather than driving their target V1 cells (Hirsch and Gilbert 1991; Hupe et al. 1998; Mignard and Malpeli 1991; Sandell and Schiller 1982; Yoshimura et al. 2000), their contribution to LFPs could be much larger than their contribution to neuronal spiking. Furthermore, whereas some studies have suggested that LFPs integrate signals locally, other studies have indicated that the latter may instead arise from several millimeters of cortex (see Introduction). For all these reasons it was unclear whether GW models, devised to explain the spiking properties of single V1 neurons, could successfully predict stimulus-evoked LFP responses, especially under naturalistic conditions. Our finding that GW models are good predictors of both LFP and spiking responses supports previous studies that have reported significant correlation between the spiking response in the immediate vicinity of the recording electrode and the LFP signal (Burns et al. 2010). This is also consistent with a previous observation that applying linear filtering on the spiking responses of a few neurons explains a significant fraction of LFP responses recorded from the same site (Rasch et al. 2009). However, this does not rule out the possibility that LFPs and spikes, in addition to similar information, also carry independent information (Belitski et al. 2008). For example, LFP responses carry significant information about stimuli presented in the modulatory region of the RF, i.e., in the RF surround, whose stimulation does not evoke spikes (Hwang and Andersen 2012; Shushruth et al. 2011) in the absence of RF stimulation. An alternative or additional explanation for our results is that if LFP signals in our experimental paradigm indeed reflect activity from a local pool of neurons, the topographic and columnar organization of V1 (due to which neighboring neurons share similar RF properties) could lead to similarity, and therefore to a correlational relationship, between LFP and spiking responses. Thus, in higher cortical areas lacking this fine architecture, there may be differences in stimulus representation between spikes and LFPs. Although GW models are good predictors of LFP responses, their performance is limited by the simplistic nature of this model. It is the goal of our future studies to test extensions to this model and alternative models by using an approach similar to that used in this study.

Informative Features of LFPs

LFP is a continuous time voltage signal. Although “spiking rate” is generally thought to be at least one informative feature of a neuron spiking response, it is unclear what features of the LFP are similarly informative. The signal range has been previously shown to carry information about object encoding in inferotemporal cortex (Kreiman et al. 2006) and about hand movement target and velocity in motor cortex (Mehring et al. 2003). Similarly, we find that among the scalar features we have considered, models estimated from the LFP signal range allow for best image identification and thus are most informative. Moreover, we find that this information is contained in the first 300 ms of the LFP response. This time window corresponds to the mean intersaccadic interval previously reported in free-viewing monkeys (Vinje and Gallant 2000). In the frequency domain, different spectral bands have been proposed to carry specific information about the stimuli. In particular, oscillations in the gamma band (30–80 Hz) have been shown to dominate during visual stimulation, although it is unknown whether they play a functional role or are just a reflection of local network activity (Berens et al. 2008b; Fries 2009). Recent reports have suggested that the stimulus selectivity of the gamma band can be different from the stimulus selectivity of the spiking activity at the same location (Jia et al. 2011; Ray and Maunsell 2011). In particular, these studies suggested that the gamma band reflects activity over a larger cortical region than spiking activity. Our results support these findings, in that we have found that the power in the gamma band of the LFP carries less information than the range of the LFP signal during natural image stimulation, as would be expected if the former integrated activity over a larger cortical region than the latter. Moreover, we found similar image identification performance of the model for all different frequency bands of the LFP, suggesting that information about natural images is not carried by a specific oscillatory component, but rather is distributed across the short-latency broadband LFP response, and that each band likely carries slightly different information. Therefore, this also suggests that the dominant gamma-band responses previously observed in V1 during visual stimulation (reviewed in Berens et al. 2008b; Fries 2009) are not just related to the information content of visual stimuli but possibly also reflect a stimulus-independent internal state of cortical circuits.

Visuospatial Spread of LFP Signals

Our approach also allowed us to investigate the visual region over which LFP signals carry visual information about natural images. The visual spread of the LFP results from the electrical spread of the signal in the cortical tissue and the spread due to connectivity (both local and long range). Several studies have examined the spatial extent of the cortical region that generates LFP signals. Three studies in V1 of anesthetized macaques or cats, using simple grating stimuli, suggested that the scale of integration is about 500–800 μm in diameter (Berens et al. 2008a; Katzner et al. 2009; Xing et al. 2009). Measurements in MT of awake macaques also suggested a local scale of about 400 μm (Liu and Newsome 2006). In contrast, other studies in inferotemporal (Kreiman et al. 2006) and auditory cortices (Kajikawa and Schroeder 2011), using more complex stimuli, have suggested a much larger area of integration. Only one of the above studies (Xing et al. 2009) relied on a more direct measure of the LFP spread based on the use of small stimuli (0.2°) and the retinotopic map of V1, and determined that LFPs propagate locally (500-μm diameter) within macaque V1. In contrast, all other studies relied on indirect estimates based on associating the LFP with columnar structures of certain feature selectivities, e.g., orientation, direction, or speed. These measurements, therefore, are based on the assumption that broader tuning of the LFP is due to wider spatial integration by the LFP compared with single units, an assumption that may only partially be correct (Jia et al. 2011). No previous studies have directly addressed the contribution of long-range connectivity to LFP signals. However, we have recently observed that LFPs in macaque V1 can be recorded at large distances (>10° of visual space) from the stimulated regions (Shushruth et al. 2011). The approach we used in the present study only allowed us to determine the combined contributions to the LFP signal of electrical spread and spread due to long-range connectivity, i.e., the visual region over which LFP signals carry information about natural images. The visual stimuli we used encompassed the RFs and near-surround region of the recorded neurons, and therefore the recorded LFPs should have reflected information from both regions. We found that the GW model performed best when the size of the wavelets was 0.45°. At the eccentricities of our recordings (centered at 7.5° or 5.5°), this corresponds to about 500–700 μm of cortical space (Van Essen et al. 1984). Given that a full cycle of orientations in macaque V1 extends on average about 760–800 μm (Bartfeld and Grinvald 1992; Obermayer and Blasdel 1993; Vanduffel et al. 2002) and that a single orientation domain is about 300–500 μm in diameter (Blasdel 1992; Ts'o et al. 1990; Vanduffel et al. 2002), 500–700 μm of cortical space encompass more than a single orientation column but less than the full diameter of an orientation hypercolumn. Consolidating this finding, we found that best model performance was obtained by a GW model including four different wavelet orientations but that increasing the number of orientations to eight did not improve performance. This suggests that the LFP pools spatial information over a few orientation columns in V1 (and hence cannot resolve finer orientation differences) but less than a full orientation hypercolumn (because it does contain enough information to resolve 4 orientations). In contrast, a similar model trained on MUA responses, at least in the anesthetized monkey, showed a small but significant improvement in performance when eight orientations were included, suggesting a more local integration region for MUA compared with LFPs. Although these results may seem to support a local origin of the LFP, what they truly show is that stimulus-specific information can be extracted at a very local level from the LFP signal, when both the RF and near-surround regions are stimulated. A recent report showed that different stimulation paradigms cause LFP signals to integrate at different spatial scales (Jia et al. 2011). Therefore, it is possible that surround stimulation in the absence of RF stimulation recruits exclusively long-range connectivity and evokes LFPs at large distances from the stimulated regions (Shushruth et al. 2011). Recently, a detailed biophysical model of the spatial reach of the LFP demonstrated that the size of the cortical region generating the LFP also depends on the correlation in synaptic activity. Specifically, contributions to LFP signals arise from smaller regions when the contributing cells are uncorrelated in their activity, but they arise from larger regions for correlated inputs (Linden et al. 2011). Accordingly, different stimulation paradigms could result in different levels of correlations between the synaptic currents contributing to the recorded LFP. In the context of our study, natural image stimulation is known to decorrelate neuronal spiking responses (Vinje and Gallant 2000), thus possibly resulting in LFP signals with smaller visuospatial reach. In summary, our study extends previous results (Berens et al. 2008a; Katzner et al. 2009; Xing et al. 2009) by suggesting that the LFP area of integration is small even when the LFP response is evoked by natural stimuli involving the near receptive field surround of the recorded cells.

GRANTS

We are grateful for support from National Science Foundation Grants IOS-0848106 and IOS-1355075 (to A. Angelucci), National Eye Institute Grants EY022757 and EY019743 (to A. Angelucci) and EY019363 (to B. Greger), U.S. Army Telemedicine & Advanced Technology Research Center Grant W81XWH-06-1-0497 (to B. Greger), a University of Utah Research Foundation Seed Grant (to T. Tasdizen), and a grant from Research to Prevent Blindness, Inc., to the Department of Ophthalmology, University of Utah.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

M.S., S.S., T.D., J.M.I., P.A.H., and A.A. performed experiments; M.S. and S.S. analyzed data; M.S., S.S., B.G., A.A., and T.T. interpreted results of experiments; M.S., S.S., and A.A. prepared figures; M.S., S.S., A.A., and T.T. drafted manuscript; M.S., S.S., B.G., A.A., and T.T. edited and revised manuscript; M.S., S.S., B.G., A.A., and T.T. approved final version of manuscript; S.S., B.G., A.A., and T.T. conception and design of research.