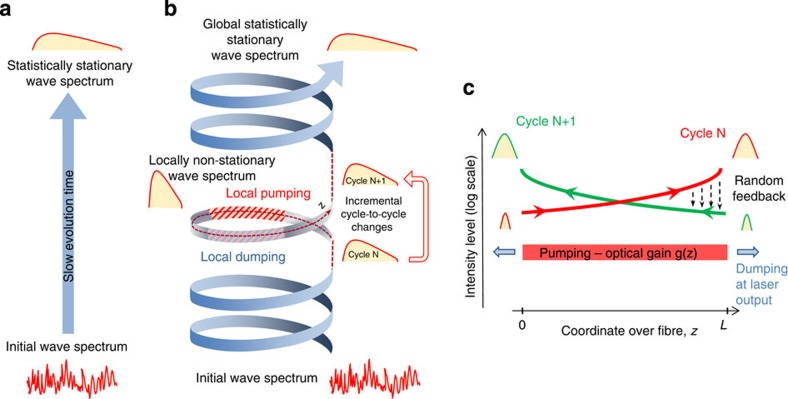
Figure 1. Wave kinetics in active cyclic systems.

(a) In classical wave kinetics, initial wave spectrum evolves gradually to a statistically stationary wave spectrum when energy pumping/dumping is homogeneous over the evolution time. The evolution is governed by wave kinetic equation. The global statistically stationary wave spectrum is also a local stationary solution, that is, does not changed when shifted in time on any arbitrary value. (b) In active cyclic systems, the energy pumping/dumping act in a periodic way resulting in cycling dynamics and double-scale evolution of the wave spectrum. When the energy pumping/dumping changes within the cycle, the wave spectrum is locally non-stationary exhibiting strong changes within each cycle. This evolution is governed by a local pumping-driven wave kinetic equation equation (3). At the same time, the spectrum evolves in a gradual incremental way from cycle to cycle similar to classical wave kinetics. If the overall pumping within the cycle is equal to energy dumping, the system approaches the global stationary solution. (c) In a random fibre laser, the optical pumping is distributed over the fibre, while the dumping occurs at fibre ends where the radiation goes out. Each pass of the optical fibre is one cycle. The generation spectrum exhibits strong changes during evolution within each cycle because of optical gain. Random distributed feedback couples the optical spectrum on consequent cycles. As the gain is equal to losses in a laser, the optical spectrum must be identical on different cycles. Thus, the global stationary solution does exist.