FIG. 3.
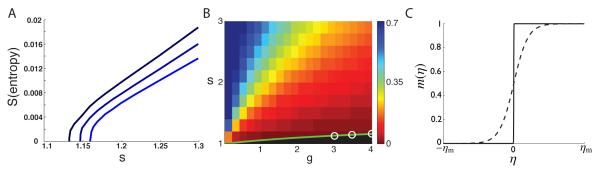
The entropy as a function of s and g, which is 1/N times the average (over J) of the logarithm of the number of stable fixed points in the network model. In both plots, the entropy goes to 0 at the values of s and g corresponding to the phase transition between the nonzero fixed-point and persistent chaotic regions in figure 1. A) The entropy as a function of s for, from top to bottom curves, g = 3, 3.5 and 4. B) The entropy over a range of s and g values represented by colors. The green line shows where the entropy reaches 0. The white circles indicate the results obtained from the zero intercepts of the curves in A. C) The weighting function m(η) near the transition (solid curve; s=1.133 and g=3) and away from the transition (dashed curve; s=1.135 and g=3).
