Abstract
The nucleation-growth model has been used extensively for characterizing in vitro amyloid fibril formation kinetics and for simulating the relationship between amyloid and disease. In the majority of studies amyloid has been considered as the dominant, or sole, aggregation end product, with the presence of other competing non-amyloid aggregation processes, for example amorphous aggregate formation, being largely ignored. Here, we examine possible regulatory effects that off-pathway processes might exert on the rate and extent of amyloid formation – in particular their potential for providing false positives and negatives in the evaluation of anti-amyloidogenic agents. Furthermore, we investigate how such competing reactions might influence the standard interpretation of amyloid aggregation as a two-state system. We conclude by discussing our findings in terms of the general concepts of supersaturation and system metastability – providing some mechanistic insight as to how these empirical phenomena may manifest themselves in the amyloid arena.
Over the last fifty-years the product of a particular class of protein aggregation reaction, known as amyloid, has come to the fore as the potential instigator of a disparate range of diseases collectively termed amyloidosis [1–3]. The current mechanistic paradigm of amyloid formation describes it as comporting to a nucleated-growth (NG) model akin to that used to describe crystal formation [3–8]. The NG model may be simply interpreted as a sequential-stepwise-process first involving a relatively slow/unfavorable primary nucleation event (capable of creating the basic amyloid structural unit) which is then followed by a rapid/favorable growth stage in which the basic amyloid unit can undergo growth by monomer addition/monomer loss, fibre joining/fibre breakage or a mixture of the two (Eqn. 1) [3,9,10]. Changes in the individual parameters expressed in Eqn. 1 have predictable consequences (described in Table 1) on the amyloid kinetic profile. It is this regular correspondence that allows both empirical assignment and mechanistic causation to be inferred from the differential kinetic behavior exhibited by amyloid when grown under two types of conditions [3,4,6,11].
Table 1.
Consequences for Amyloid Kinetics of Parameter Changes within the Nucleation-Growth Model
| Parameter# | Consequences* |
|---|---|
| Monomer concentration (M) |
|
| Nucleation rate (kn+, kn−) |
|
| Nucleation size (n) | In the classical Oosawa-Asakura model of helical polymer formation [7], an increase in the molecularity^ of the nucleation reaction will lower the concentration of the critical nucleus. This will concomitantly |
| Growth rate by monomer addition (kg+) | Increasing the rate of monomer addition to amyloid fibrils will tend to (1) increase the rate of amyloid formation (weight concentration) [8,21] (2) increase the size distribution of amyloid (average molecular weight) |
| Dissociation rate by monomer loss (kg−) | Slower rates of monomer dissociation from amyloid fibrils will tend to
|
| Fiber breakage rate (kb) | Fiber breakage rates have been shown to display different behaviors.
|
| Fiber joining rate (kj) | The effect of variation in fiber joining rate on both the rate of amyloid formation and the amyloid fiber distribution properties has been less well studied [9,10]. Intuitively, we may propose that increasing the fiber joining rate will,
|
Parameters refer to rate constants governing the elementary steps of the nucleated growth scheme shown (Eqn. 1).
Here we draw a distinction between two types of amyloid growth. The first refers to the total mass of monomer incorporated into amyloid i.e. weight concentration. The second refers to the general size of the amyloid size distribution i.e. average molecular weight [8,22,23].
By molecularity we mean the number of molecules involved in the reaction.
| [1a] |
| [1b] |
| [1c] |
| [1d] |
The characteristic empirical behavior encoded in Eqn. 1 and described in Table 1 is predicated upon the experimental system conforming to a single class of aggregation pathway. For the in vitro case, experimental conditions can be achieved which satisfy the requirement of yielding a single structural class/strain of amyloid fiber [12,13]. However under ‘non-optimized’ in vitro conditions [14–18], or under non-controllable in vivo situations [19,20], there is no guarantee that the experimental system will conform to such a single pathway requirement [3,11]. In such cases, aggregation may occur along multiple pathways with a variety of protein aggregation products, both amyloid and other types, being produced [13–15]. As a result the standard consequences arising from a nucleated growth-type mechanism for amyloid (outlined in Table 1), previously taken to be axiomatic, may not be applicable.
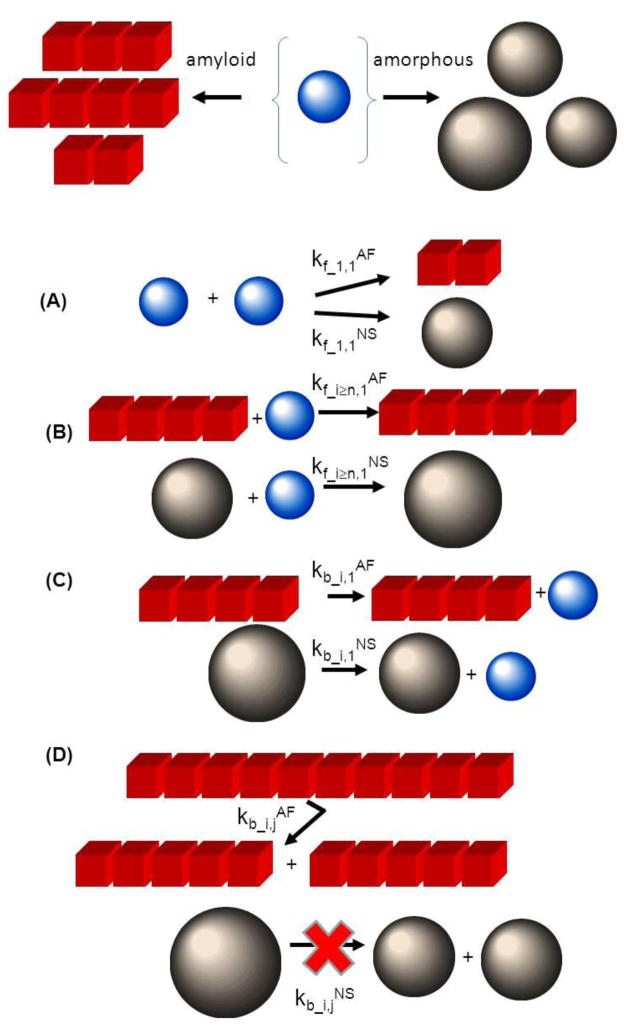
In the current work, we have examined likely possible effects of the existence of competing aggregation reactions on the time course and equilibrium extent of amyloid formation. Two modes of protein aggregation, amyloid formation and non-specific agglomeration 1, were considered to be in direct competition for a common pool of monomer (Fig. 1). Amyloid formation was treated as a one-dimensional nucleated growth process [3,8,22–24]. In the mathematical realization of this model, all chemical species were simulated using an explicit approach [23] featuring fibril nucleation, fiber growth by monomer extension and internal and end-fragmentation of polymer (Fig. 1). The size-specific forward and backwards rate constants governing the amyloid formation reaction 2 are respectively denoted by kf_i,1AF and kb_i,jAF. The non-specific aggregation process was considered as a series of diffusion limited reactions3 for which the aggregate can reversibly grow and shrink through monomer addition and monomer loss (Fig. 1). As for the amyloid fibers, the non-specific agglomeration process was also modeled explicitly, with the rate constants for each step assigned on the basis of a diffusion collision model which considered the ith aggregate (i.e. aggregate species composed of i monomers) to have geometric properties defined by the following relationships for volume, V and radius, R; Vi = iV1; Ri = [3iV1/(4π)]1/3. For the interaction of one spherical species with another, the diffusion collision scheme predicts a functional dependence of the growth rate on monomer size as per Eqn. 2a (justification provided in Appendix 1). Assuming that monomer contained within non-specific aggregate can dissociate most easily from the aggregate’s surface we have set the size specific dissociation rate constant proportional to surface area (Eqn. 2b).
Figure 1. TOP- Schematic mechanism reflecting competition for monomer (small blue spheres) between amorphous aggregation (black spheres) and amyloid formation (red cubes). BOTTOM- Four distinct types of elementary process are considered in the competitive aggregation mechanism.
(A) Nucleation: describes the formation of a key structural or energetic intermediate that represents the bottle neck for further aggregate growth. Kinetics are respectively specified by a series of bimolecular reactions involving monomer addition to the growing pre-nucleus with second order forward nucleation rate constants, kf_i<n,1AF (amyloid) and kf_i<n,1NS (non-specific aggregation) having units of M−1s−1. In the current case, nucleus size, n, is arbitrarily modeled as a dimer for both modes of aggregation (i.e. n = 2). (B) Growth: Growth of both amyloid and non-specific aggregate is considered to occur via monomer addition with respective second-order forward rate constants written as kf_i≥1,1AF (amyloid) and kf_ i≥1,1NS (with units of M−1s−1). The growth stage for amyloid formation is characterized by kf_i>n,1AF ≫ kf_i<n,1AF whilst the growth stage for non-specific aggregation is defined by kf_i>n,1NS = kf_i<n,1NS (i.e. no distinction between nucleation and growth stages). (C) Breakage via monomer release: Both non-specific aggregate and amyloid are considered to be able to decrease in size through release of monomer, which subsequently reclaims its structural state operative under the particular solution conditions (blue sphere). Breakage resulting in monomer release for each type of aggregate is defined by first order rate constants kb_i,1AF and kb_i,1NS having units of s−1. In this paper both non-specific and amyoid monomer release rates were assigned equal to the common value kb_1,1. (D) Breakage resulting in release of two smaller aggregate species: This mode of breakage, describing the division of an aggregate of size i+j into two separate aggregates of size i and j, was defined by a set of breakage rate constants kb_i,jAF and kb_i,jNS for the amyloid and non-specific aggregation cases respectively. However only amyloid was considered as being able to undergo appreciable internal fragmentation i.e. kb_i,jAF > 0. All internal modes of breakage were considered equal for the amyloid case such that kb_i,jAF = kb_i,1AF (for all i,j). As the non-specific aggregate was modeled as a sphere, internal fragmentation was considered much less likely than monomer release i.e. kb_i,jNS ≈ 0.
| [2a] |
| [2b] |
The values of forward and backward rate constants for the amorphous aggregation reaction (that form the basis for the scaling in Eqn. 2) were chosen to explore the often invoked assumption – that amyloid represents the lowest energy structural state available to the protein [27,28]. Due to their presumed diffusion limited nature (Eqn. 2) we set the values of kf_11NS and kb_11NS in relation to kf_1,1AF and kb_1,1AF to affect behavior in which non-specific aggregate was formed faster but was ultimately less thermodynamically stable than the competing amyloid. Based on the relevant experimental procedures [29–32] we transformed the simulated time courses into an equivalent pseudo-experimental signal based on the following two experimental observations. Observation 1: All species heavier than the monomer can be differentially sedimented or filtered and therefore both non-specific aggregate and amyloid are retained in the pellet/filter [29,31]. Observation 2: Amyloid exhibits a positive Thioflavin T binding response whereas non-specific aggregate exhibits no Thioflavin T binding ability [30,32].
Results
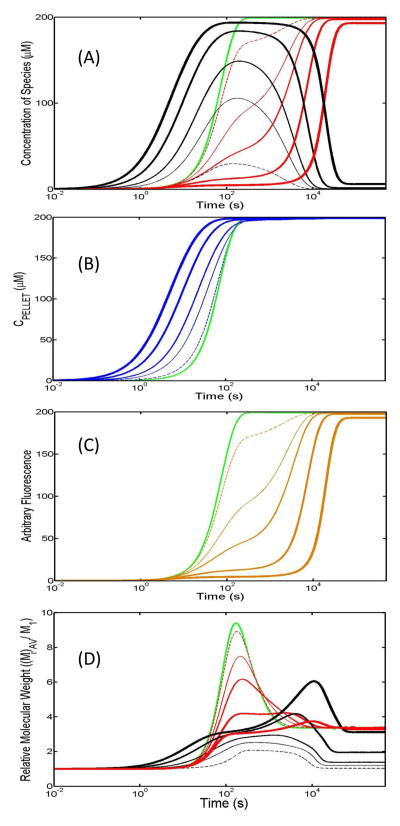
Six different cases of an aggregation reaction were simulated in which amyloid growth competed against amorphous aggregation for monomer (Fig. 2). Fig. 2A represents a species plot description of the temporal evolution of amyloid (red lines) and non-specific aggregate (black lines) components. The fundamental rate constants defining the non-specific agglomeration component of the aggregation reaction were varied through the six simulations to transition from relatively fast to relatively slow aggregation. In this study, fast and slow designations are made relative to the rate of amyloid formation (see figure legend). In the absence of competition by amyloid, all sets of non-specific agglomeration rate constants would incorporate practically all monomer into the non-specific aggregate form.
Figure 2. Simulation of the kinetics of amyloid versus non-specific aggregate growth in a situation whereby both modes of aggregation are competing for a common pool of monomer.
Amyloid formation was defined throughout all kinetic simulations by a set of common rate constants (values listed below) which, in the absence of any competing non-specific aggregation pathway, would return an identical kinetic profile (green lines). The fundamental rate constants defining the non-specific agglomeration component of the aggregation reaction were varied from relatively fast to relatively slow aggregation carried out in six stages (values described below). (A) Time-dependent species plot: The two types of competing aggregate from a single simulation are designated by lines of the same thickness/marking pattern with black referring to non-specific aggregate and red describing amyloid formation. (B) Time-dependence of total aggregate: The total mass of aggregate, amyloid and non-specific agglomerate, as a function of time (as would be recorded by filter binding or pelleting assays). (C) Time-dependence of Thioflavin T binding: Simulated signal observed for Thioflavin T dye binding assay which exhibits a positive fluorescence signal when bound to aggregate species having a stacked intermolecular beta-sheet character i.e. amyloid. (D) Time-dependence of relative molecular weight: Simulated case where aggregates are first separated into their various types prior to determination of their relative molecular weight. Parameters for amyloid rate constants and six stages of variation in non-specific rate constants (1) Amyloid: (kb_i,jAF = 5×10−4s−1, kf_1,1AF = 10M−1s−1, kf_i>1,1AF = 1000M−1s−1) (2) Non-Specific Aggregation: Set 1: fastest agglomeration (thickest line, kb_1,1NS = 5×10−4s−1, kf_1,1NS = 500M−1s−1), Set 2: second fastest agglomeration (second thickest line, kb_1,1NS = 5×10−4s−1, kf_1,1NS = 250M−1s−1), Set 3: third fastest agglomeration (third thickest line: kb_1,1NS = 5×10−4s−1, kf_1,1NS = 100M−1s−1), Set 4: fourth fastest agglomeration (fourth thickest line: kb_1,1NS = 5×10−4s−1, kf_1,1NS = 50M−1s−1), Set 5: slowest agglomeration (thindashed line: kb_1,1NS= 5×10−4s−1, kf_1,1NS = 10M−1s−1), Set 6: no agglomeration (green line: kb_1,1NS=0s−1, kf_1,1NS=0M−1s−1).
From the information provided in the species plot progress curves, we sought to develop a range of realistic experimental measures of the aggregation process. Two closely related procedures for monitoring the progress of an aggregation reaction involve either the centrifugal or filtration-based separation of all species larger than a predetermined size limit – commonly chosen to be that of the monomer4 [30,31]. Fig. 2B describes the total amount of protein that would be recorded by such a pelleting/filtration assay for the six simulation cases described in Fig. 2A (thick to thin blue lines representing transition from fast to slow non-specific aggregation with green line representing zero non-specific aggregation). Note that the classical sigmoidal pattern typically associated with amyloid formation is restored. Another frequently-used procedure for recording the kinetics of amyloid formation involves the use of amyloid specific dyes such as Thioflavin T [29,32] and Congo Red [33]. These dyes show a concerted change in spectral properties upon binding to amyloid and can thus provide a near continuous measure of its formation. Fig. 2C describes the simulated fluorescence trace that would be recorded for a Thioflavin T dye-binding analysis of amyloid formation over the six simulation cases (thick to thin orange lines representing fast to slow transition in the agglomeration reaction with green line describing a zero rate). Techniques based on the measurement of light scattered from purified aggregate fractions (such as DLS and SEC-MALLS [34,35]) can provide some information on the size distribution and structure of the aggregate – such as average molar mass. Fig. 2D shows the time dependence of the number average molecular weight of two types of aggregate, amyloid (red) and non-specific agglomerate (black) over the six simulation cases explored (thick to thin lines describing the transition from fast to slow agglomeration rate).
Discussion
Perhaps the most remarkable feature of the current study is the degree to which the inclusion of a competing non-specific pathway can radically change the shape and characteristic kinetics of the amyloid progress curve (Fig. 2C). This point is notable for two different reasons relating to (i) in vitro screening of potential anti-amyloid agents/conditions, and (ii) modelling of the role of amyloid in amyloidosis diseases.
With regard to point (i.) in vitro screening of anti-amyloid agents; oftentimes, the underlying goal behind an amyloid formation assay is the evaluation of the ability of a drug, ligand, or set of buffer conditions to limit amyloid growth [36–44]. As indicated by the current simulations, there is significant potential for any observed anti-amyloid effect to be due to stimulation/retardation of a competing pathway, which may/may not be operative under the pertinent in vivo conditions. Further to this point, when comparing the anti-amyloid effect of drug/buffer conditions between two different model systems, the lack of a common set of competing aggregation pathways between the systems may complicate the interpretation of the screening results if the drug/conditions differentially stimulate the competing pathways particular to each system. One such example of a potentially complicated drug action comes from the apparent inhibition of various amyloid species by the flavonoid (−)-epigallocatechin 3-gallate (EGCG) [45–47]. Dispute over the exact nature of the anti-amyloid mechanism of EGCG stems from its contested dual potential to either stabilize competing micelle-products [46] or destabilize the amyloid directly [45,47]. In the light of the findings of the present study, the potential for the absence of a direct anti-amyloidogenic activity of this inhibitor is extant. Another example of the potential complicating effects of a competing pathway lies in the work of Chiti and coworkers who sought to define the factors affecting the absolute reaction rates of protein aggregation [48–51]. The mainstay of these early studies was muscle acyl phosphatase – a protein shown by the same authors to form both amyloid and amorphous aggregation products [51]. Their adopted algorithmic approach involved parameterizing the effects of variations in temperature, ionic strength, pH and protein intrinsic factors in terms of aggregation kinetics recorded by pelleting assay and Thioflavin T dye binding assays. The findings presented in the current paper suggest that care must be placed in the choice of basis set data for formulation of any such amyloid propensity scales [49,50] due to the many orders of magnitude differences that may potentially be brought about by the presence of a competing pathway (Fig. 2).
With regard to point (ii) modelling of the role of amyloid in the amyloidosis diseases; the main aim in using kinetic-rate-model simulations in amyloidosis research lies in the exploration of possible linkages between amyloid formation and the different stages of disease onset/symptomatic display [3,23]. Due to its fundamental connection to the underlying chemical physics, the NG paradigm has been the mainstay of such modelling efforts in vitro [3,5,6,11,28]. However in transitioning from the test-tube to the patient, many have assumed that amyloid formation in the body may be describable in terms of the framework of the NG model, and have used this model as a chemical scaffold upon which to build theories of disease progression [3,23,52,53]. In such a conceptualization the chemical environment in which the protein is placed is implicitly considered in the sense that it may act to alter the statistical likelihood of an individual step in the pathway but is not fundamentally required for the step to occur – i.e. the human body is treated as a reaction vessel defining a unique set of rate constants for Eqn. 1. However the presence of a competing pathway will upset this deterministic conceptualization of aggregate growth. In the current study the presence of a competing pathway has been shown to be operationally equivalent to a complex time dependent function of the availability of free protein i.e. CM(t) = f(t;X1,X2,..). Such a time-dependent functionalization of the free monomer concentration in terms a set of parameters [X1, X2,..] has not been widely (if at all) discussed prior to this point. However consideration of such a functionalization of CM may prove particularly insightful to understanding the causation and timing of amyloidosis disease onset. For example an increased production of protein monomer, as for leukemia related overproduction of antibody light chain in AL amyloidosis, may be sufficient to cause disease phenotype/symptomatic display [54]. As previously noted such a disease switch point may take the form of a change in free monomer concentration, a change in total amyloid loading or a change in the loading of a particular subsection of the amyloid distribution (Fig. 2) [3,23].
A final point worthy of discussion is the general similarities that can be drawn between the kinetic behavior observed in the current simulations and the physical phenomenon of supersaturation [55,56]. Supersaturation describes a non-equilibrium state of a system for which its full transition to its new equilibrium state has been kinetically limited thereby leading to a long-lived metastable intermediate. One pertinent example of supersaturation is the ability to increase a liquid’s dissolved gas content above its known solubility limit, when the liquid lacks competent nucleation centers for bubble formation such as might be produced by containers possessing pitted walls capable of accommodating significant amounts of dissolved gas [57,58]. At a purely empirical level the simulations in the current paper describe a slow kinetic transition from initial monomer to final amyloid states (Fig. 2) which proceed via formation of a non-specific aggregate intermediate (NS-AGG) (Eqn. 3).
| [3] |
In this context we note that the kinetically limited transition of protein to the amyloid state observed in the current studies can, by analogy, be interpreted as a supersaturation process [14,57,58] 5. In general the relative coarseness of the experimental measurement techniques used to record the formation of amyloid oftentimes impose an artificial ‘two-phase’ conceptualization upon the system i.e. the measurement signal either designates the protein as soluble monomer or aggregate (Eqn. 4a – Fig. 2B) or alternatively as amyloid fiber or non-amyloid fiber (Eqn. 4b – Fig. 2C).
| [4a] |
| [4b] |
Although higher-order structural and analytical methods are capable of providing a richer picture of the heterogeneous nature of the aggregate distribution (Fig. 2D), necessarily over-simplistic strategies, employed in the data-reduction associated with these techniques, also lead to a similar two-phase interpretation being imposed upon the system post-experiment. So, whether due to limitations of the experimental methodology or of the methods used for data reduction/analysis, the operative transition for study is a type of two-state transition as represented by Eqn. 4. However, the complex multi-phase kinetics of amyloid production seen in Fig. 2c does not easily comport to such a two-state system. In light of the previous discussion of supersaturation, the non-specific protein aggregate form presents itself as an obvious candidate for the metastable species responsible for supersaturation-like delayed production of the amyloid phase from the monomer [14,44,46,55–58].
In conclusion, this study has highlighted some of the empirical consequences of a protein aggregation mechanism possessing an amorphous competing reaction pathway in addition to the amyloid forming pathway. The real-life manifestations of such a competitive growth scheme will undoubtedly be more complex than the simple two-state system investigated here. We briefly discuss some of the higher order complexity that may be introduced by multiple competing species in Appendix 2. However we believe that the general physical principles which determine the system behavior are captured within this study and therefore our results may prove instructional to others working on the same, or closely related, problems.
Acknowledgments
DH would like to acknowledge Dr. Nami Hirota for comments received on an early draft of this manuscript.
Funding Sources
The research of D.H. is supported by an A.N.U. Senior Research Fellowship. The research of J.K. is supported by a Bolyai Janos fellowship from the Hungarian Academy of Sciences. The research of J.A.C. is supported by a Project Grant from the National Health and Medical Research Council of Australia. The research of Y.G. is supported by the Japanese Ministry of Education, Culture, Sports, Science and Technology. The research of H.E. was supported in part by the Intramural Research Program of the NIH, National Institute of Diabetes Digestive and Kidney Diseases.
Abbreviations
- NG
Nucleated Growth
- NS-AGG
Non-Specific Aggregate
Appendix 1: Size dependence of non-specific aggregation
The diffusive collision rate between a spherical aggregate of i monomers and a monomer (of radius Ri and R1 respectively), can be calculated directly from Fick’s Laws [A1,A2]. The per unit area flux, j1, (molecules m2s−1) of monomers across some region of surface surrounding an (initially) stationary aggregate i is given by,
| [A1] |
Here D1 represents the monomer diffusion constant (m2s−1) and r denotes the radial distance of the flux boundary from the center of the aggregate i. The total flux of monomer, J1, (molecules s−1) through this surface region is,
| [A2] |
The total rate of collisions occurring at Ri1 (where Ri1 = Ri +R1) can be obtained by separating and integrating the differential (Eqn. A3).
| [A3] |
Relaxing the requirement for aggregate i to be stationary and expressing the total flux in terms of the rate of molar collisions between aggregate i and monomer yields Eqn. A4.
| [A4] |
Setting the diffusion constant for a spherical aggregate composed of i monomers to be Di = kT/(6 πηRi) where η is the dynamic viscosity of the solvent yields a dependence of the associative collision rate Ji1 on the size of aggregate i and monomer. The previous development can be used to show that the forward rate of reaction scales with both the ratio of diffusion constants and the ratio of the collisional radius Ri1 = Ri+R1, yielding (Eqn. A5a). With regards to dissociation from the aggregate: for a spherical aggregate shape the rate of monomer release from the aggregate is taken as a first-order process which scales with the ratio of surface area (Eqn. A5b).
| [A5a] |
| [A5b] |
Expansion of equations A5a and A5b along with their subsequent combination with the non-specific volume relations described prior to Eqn. 2a yield Eqn. 2 in the main article. Interestingly, the theoretical development employed here, based solely on diffusive encounter arguments, yields a one-third power dependence for the aggregate rate constant on aggregate size rather than the two-thirds power dependence predicted based on mean free path and collisional cross section arguments derived for particle motion in the gas phase. This difference represents an important distinction between these two regimes. A recent study by Stranks et. al. [A3] develops an alternative result to the one presented here. By application of scaling arguments, they derive an analytical equation suggesting that the non-specific rate of incorporation of monomer by spherical aggregates in the diffusion limited regime should exhibit a two-thirds power dependence on particle size. Interestingly much of the supporting experimental data on amorphous aggregation in the study by Stranks et al. [A3] reflects an experimental value closer to 1/3 than 2/3. Higher values of the exponent may signify fractal-like growth kinetics due to increasing reactive surface area associated with an irregular non-specific aggregate surface. Alternatively, the several assumptions required in that work to develop a set of kinetic equations from the scaled data may not be in the strongest form (i.e. assumption of irreversible aggregation, assumption of turbidity as a linear descriptor of aggregate mass concentration).
Appendix 1 References
- A1.Hammes GG, Schimmel PR. Rapid Reactions and Transient States. In: Boyer PD, editor. The Enzymes. Vol. 2. New York: Academic Press; 1970. pp. 67–68. [Google Scholar]
- A2.Cantor CR, Schimmel PR. Biophysical Chemistry. W.H. Freeman and Company; 1980. Chapter 16, Kinetics of Ligand Interactions; pp. 920–921. [Google Scholar]
- A3.Stranks SD, Ecroyd H, Van Sluyter S, Waters EJ, Carver JA, von Smekal L. Model for amorphous aggregation processes. Physical Review E. 2009;80:051907. doi: 10.1103/PhysRevE.80.051907. [DOI] [PubMed] [Google Scholar]
Appendix 2: Potential complexities introduced by the existence of multiple competing species
In the main paper we have modeled competition between amyloid and non-specific agglomerate as a contest for monomer between just two structural forms of aggregate. In reality however it is likely that multiple sub-types of each aggregate may exist. This situation would yield an equation of the form [A6] for the total balance of populations (defined in terms of the constituent concentrations CAMYLOID and CNON-SPECIFIC). Equation A6 can be interpreted with reference to a generalized nomenclature, (CAGG)qM which describes an aggregate of degree of polymerization, q, of sub-type M, at a number concentration C.
| [A6a] |
| [A6b] |
The existence of a series of cascade like reactions in which monomer is shuttled from one form to another before finally reaching a low energy amyloid state would further complicate the metastability issue addressed in the main paper. Interestingly the introduction of a higher-order conceptualization of the aggregate space would also greatly complicate the search for the assumed toxic component of the aggregate distribution.
Footnotes
We use the terms non-specific agglomeration, non-specific aggregation and amorphous aggregation interchangeably throughout this paper.
Although a method has been developed for assigning size dependent values for these rate constants for a linear growth model [24,25] here we have simplified the process by assigning a set of fixed values for the respective nucleation, growth and breakage steps.
The diffusion limited regime has historically been termed as perikinetic aggregation [26].
A very similar result is produced by filter binding/filtration assay [31].
In that its concentration dictates a phase shift which is slow to occur due to a long-lived metastable intermediate.
The authors declare no competing financial interests.
Author Contributions
DH and YG conceived the idea for the paper. DH performed the simulations. DH, JK, HE, JC and YG wrote the paper.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Merlini G, Seldin DC, Gertz MA. Amyloidosis: pathogenesis and new therapeutic options. J Clin Oncol. 2011;29:1924–1933. doi: 10.1200/JCO.2010.32.2271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Sipe JD, Benson MD, Buxbaum JN, Ikeda SI, Merlini G, Saraiva MJ, Westermark P. Amyloid fibril protein nomenclature: 2012 recommendations from the Nomenclature Committee of the International Society of Amyloidosis. Amyloid. 2012;19:167–170. doi: 10.3109/13506129.2012.734345. [DOI] [PubMed] [Google Scholar]
- 3.Hall D, Edskes H. Computational modeling of the relationship between amyloid and disease. Biophys Rev. 2012;4:205–222. doi: 10.1007/s12551-012-0091-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Naiki H, Higuchi K, Nakakuki K, Takeda T. Kinetic analysis of amyloid fibril polymerization in vitro. Lab Investig. 1991;65:104–110. [PubMed] [Google Scholar]
- 5.Jarrett JT, Lansbury PT., Jr Seeding “one-dimensional crystallization” of amyloid: a pathogenic mechanism in Alzheimer’s disease and scrapie? Cell. 1993;73:1055–1058. doi: 10.1016/0092-8674(93)90635-4. [DOI] [PubMed] [Google Scholar]
- 6.Lomakin A, Chung DS, Benedek GB, Kirschner DA, Teplow DB. On the nucleation and growth of amyloid beta-protein fibrils: detection of nuclei and quantitation of rate constants. Proc Natl Acad Sci USA. 1996;93:1125–1129. doi: 10.1073/pnas.93.3.1125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Oosawa F, Asakura S. Thermodynamics of the Polymerization of Protein. Academic; London: 1975. [Google Scholar]
- 8.Hall D, Minton AP. Effects of inert volume-excluding macromolecules on protein fiber formation. II Kinetic models for nucleated fiber growth. Biophys Chem. 2004;107:299–316. doi: 10.1016/j.bpc.2003.09.016. [DOI] [PubMed] [Google Scholar]
- 9.Binger KJ, Pham CL, Wilson LM, Bailey MF, Lawrence LJ, Schuck P, Howlett GJ. Apolipoprotein C-II amyloid fibrils assemble via a reversible pathway that includes fibril breaking and rejoining. J Mol Biol. 2008;376:1116–1129. doi: 10.1016/j.jmb.2007.12.055. [DOI] [PubMed] [Google Scholar]
- 10.Ghosh P, Kumar A, Datta B, Rangachari V. Dynamics of protofibril elongation and association involved in Aβ42 peptide aggregation in Alzheimer’s disease. BMC Bioinform. 2010;11:S24. doi: 10.1186/1471-2105-11-S6-S24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gillam JE, MacPhee CE. Modelling amyloid fibril formation kinetics: mechanisms of nucleation and growth. J Phys Condensed Matter. 2013;25:373101. doi: 10.1088/0953-8984/25/37/373101. [DOI] [PubMed] [Google Scholar]
- 12.Qian J, Lu Y, Chia A, Zhang M, Rupar PA, Gunari N, Winnik MA. Self-seeding in one dimension: A route to uniform fiber-like nanostructures from block copolymers with a crystallizable core-forming block. ACS nano. 2013;7:3754–3766. doi: 10.1021/nn400124x. [DOI] [PubMed] [Google Scholar]
- 13.Fandrich M, Pedersen MWS, Otzen D. Amyloid fibrils and prefibrillar aggregates: molecular and biological properties. 2013. Fibrillar Polymorphism. [Google Scholar]
- 14.Ikenoue T, Lee YH, Kardos J, Yagi H, Ikegami T, Naiki H, Goto Y. Heat of supersaturation-limited amyloid burst directly monitored by isothermal titration calorimetry. Proc Natl Acad Sci USA. 2014;111:6654–6659. doi: 10.1073/pnas.1322602111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Streets AM, Sourigues Y, Kopito RR, Melki R, Quake SR. Simultaneous measurement of amyloid fibril formation by dynamic light scattering and fluorescence reveals complex aggregation kinetics. PloS one. 2013;8:e54541. doi: 10.1371/journal.pone.0054541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Stathopulos PB, Scholz GA, Hwang YM, Rumfeldt JA, Lepock JR, Meiering EM. Sonication of proteins causes formation of aggregates that resemble amyloid. Prot Sci. 2004;13:3017–3027. doi: 10.1110/ps.04831804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Qin Z, Hu D, Zhu M, Fink AL. Structural characterization of the partially folded intermediates of an immunoglobulin light chain leading to amyloid fibrillation and amorphous aggregation. Biochemistry. 2007;46:3521–3531. doi: 10.1021/bi061716v. [DOI] [PubMed] [Google Scholar]
- 18.Wood SJ, Maleeff B, Hart T, Wetzel R. Physical, morphological and functional differences between pH 5.8 and 7.4 aggregates of the Alzheimer’s amyloid peptide A β. J Mol Biol. 1996;256:870–877. doi: 10.1006/jmbi.1996.0133. [DOI] [PubMed] [Google Scholar]
- 19.Bednarska NG, Schymkowitz J, Rousseau F, Van Eldere J. Protein aggregation in bacteria: the thin boundary between functionality and toxicity. Microbiology. 2013;159:1795–1806. doi: 10.1099/mic.0.069575-0. [DOI] [PubMed] [Google Scholar]
- 20.Jimenez JL, Tennent G, Pepys M, Saibil HR. Structural diversity of ex vivo amyloid fibrils studied by cryo-electron microscopy. J Mol Biol. 2001;311:241–247. doi: 10.1006/jmbi.2001.4863. [DOI] [PubMed] [Google Scholar]
- 21.Hall D, Edskes H. Silent prions lying in wait: a two-hit model of prion/amyloid formation and infection. J Mol Biol. 2004;336:775–786. doi: 10.1016/j.jmb.2003.12.004. [DOI] [PubMed] [Google Scholar]
- 22.Hall D, Minton AP. Effects of inert volume-excluding macromolecules on protein fiber formation. I Equilibrium models. Biophys Chem. 2002;98:93–104. doi: 10.1016/s0301-4622(02)00087-x. [DOI] [PubMed] [Google Scholar]
- 23.Hall D, Edskes H. A model of amyloid’s role in disease based on fibril fracture. Biophys Chem. 2009;145:17–28. doi: 10.1016/j.bpc.2009.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hall D, Hirota N, Dobson CM. A toy model for predicting the rate of amyloid formation from unfolded protein. J Mol Biol. 2005;351:195–205. doi: 10.1016/j.jmb.2005.05.013. [DOI] [PubMed] [Google Scholar]
- 25.Hall D, Hirota N. Multi-scale modelling of amyloid formation from unfolded proteins using a set of theory derived rate constants. Biophys Chem. 2009;140:122–128. doi: 10.1016/j.bpc.2008.11.013. [DOI] [PubMed] [Google Scholar]
- 26.Elimelech M, Gregory J, Jia J, Williams R. Particle Deposition and Aggregation. Chapter 6. Butterworth and Heinemann; 1995. pp. 157–204. [Google Scholar]
- 27.Straub JE, Thirumalai D. Toward a molecular theory of early and late events in monomer to amyloid fibril formation. Annual Review of Physical Chemistry. 2011;62:437–463. doi: 10.1146/annurev-physchem-032210-103526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Knowles TP, Vendruscolo M, Dobson CM. The amyloid state and its association with protein misfolding diseases. Nature Reviews Molecular Cell Biology. 2014;15:384–396. doi: 10.1038/nrm3810. [DOI] [PubMed] [Google Scholar]
- 29.Levine H., III . Chapter 18. Quantification of β-sheet amyloid fibril structures with Thioflavin T. In: Wetzel R, editor. Methods in Enzymology: Amyloids, Prions and Other Protein Aggregates. Vol. 309. 1999. pp. 274–284. [DOI] [PubMed] [Google Scholar]
- 30.Binger KJ, Ecroyd H, Yang S, Carver JA, Howlett GJ, Griffin MD. Avoiding the oligomeric state: αB-crystallin inhibits fragmentation and induces dissociation of apolipoprotein C-II amyloid fibrils. FASEB J. 2013;27:1214–1222. doi: 10.1096/fj.12-220657. [DOI] [PubMed] [Google Scholar]
- 31.Wanker EE, Scherzinger E, Heiser V, Sittler A, Eickhof H, Lehrach Hans. Membrane filter assay for detection of amyloid like polyglutamine containing protein aggregates Chapter 24. In: Wetzel R, editor. Methods in Enzymology: Amyloids, Prions and Other Protein Aggregates. Vol. 309. 1999. pp. 375–385. [DOI] [PubMed] [Google Scholar]
- 32.Naiki H, Gejyo F. Kinetic analysis of amyloid fibril formation. Chapter 20. In: Wetzel R, editor. Methods in Enzymology: Amyloids, Prions and Other Protein Aggregates. Vol. 309. 1999. pp. 305–317. [DOI] [PubMed] [Google Scholar]
- 33.Klunk WE, Jacob RF, Preston-Mason R. Quantifying amyloid by Congo Red spectral assay. Chapter 19. In: Wetzel R, editor. Methods in Enzymology: Amyloids, Prions and Other Protein Aggregates. Vol. 309. 1999. pp. 285–304. [DOI] [PubMed] [Google Scholar]
- 34.Lomakin AL, Benedek G, Teplow DB. Monitoring protein assembly using quasielastic light scattering spectroscopy. Chapter 27. In: Wetzel R, editor. Methods in Enzymology: Amyloids, Prions and Other Protein Aggregates. Vol. 309. 1999. pp. 429–459. [DOI] [PubMed] [Google Scholar]
- 35.Sahin E, Roberts CJ. Therapeutic Proteins. Humana Press; 2012. Size-exclusion chromatography with multi-angle light scattering for elucidating protein aggregation mechanisms; pp. 403–423. [DOI] [PubMed] [Google Scholar]
- 36.Levine H, III, Scholten JD. Screening for pharmacologic inhibitors of amyloid fibril formation. Chapter 29. In: Wetzel R, editor. Methods in Enzymology: Amyloids, Prions and Other Protein Aggregates. Vol. 309. 1999. pp. 467–475. [DOI] [PubMed] [Google Scholar]
- 37.Karran E, Mercken M, De Strooper B. The amyloid cascade hypothesis for Alzheimer’s disease: an appraisal for the development of therapeutics. Nat Rev Drug Discov. 2011;10:698–712. doi: 10.1038/nrd3505. [DOI] [PubMed] [Google Scholar]
- 38.Härd T, Lendel C. Inhibition of amyloid formation. J Mol Biol. 2012;421:441–465. doi: 10.1016/j.jmb.2011.12.062. [DOI] [PubMed] [Google Scholar]
- 39.Grelle G, Otto A, Lorenz M, Frank RF, Wanker EE, Bieschke J. Black tea theaflavins inhibit formation of toxic amyloid-β and α-synuclein fibrils. Biochemistry. 2011;50:10624–10636. doi: 10.1021/bi2012383. [DOI] [PubMed] [Google Scholar]
- 40.Caruana M, Högen T, Levin J, Hillmer A, Giese A, Vassallo N. Inhibition and disaggregation of α-synuclein oligomers by natural polyphenolic compounds. FEBS Lett. 2011;585:1113–1120. doi: 10.1016/j.febslet.2011.03.046. [DOI] [PubMed] [Google Scholar]
- 41.Di Giovanni S, Eleuteri S, Paleologou KE, Yin G, Zweckstetter M, Carrupt PA, Lashuel HA. Entacapone and tolcapone, two catechol O-methyltransferase inhibitors, block fibril formation of α-synuclein and β-amyloid and protect against amyloid-induced toxicity. J Biol Chem. 2010;285:14941–14954. doi: 10.1074/jbc.M109.080390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Pandey N, Strider J, Nolan WC, Yan SX, Galvin JE. Curcumin inhibits aggregation of α-synuclein. Acta Neuropathol. 2008;115:479–489. doi: 10.1007/s00401-007-0332-4. [DOI] [PubMed] [Google Scholar]
- 43.Findeis MA. Approaches to discovery and characterization of inhibitors of amyloid β-peptide polymerization. Biochimica et Biophysica Acta (BBA)-Mol Basis of Disease. 2000;1502:76–84. doi: 10.1016/s0925-4439(00)00034-x. [DOI] [PubMed] [Google Scholar]
- 44.Johnson SM, Connelly S, Fearns C, Powers ET, Kelly JW. The transthyretin amyloidoses: from delineating the molecular mechanism of aggregation linked to pathology to a regulatory-agency-approved drug. J Mol Biol. 2012;421:185–203. doi: 10.1016/j.jmb.2011.12.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Meng F, Abedini A, Plesner A, Verchere CB, Raleigh DP. The flavanol (−)-epigallocatechin 3-gallate inhibits amyloid formation by islet amyloid polypeptide, disaggregates amyloid fibrils, and protects cultured cells against IAPP-induced toxicity. Biochemistry. 2010;49:8127–8133. doi: 10.1021/bi100939a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Hudson SA, Ecroyd H, Dehle FC, Musgrave IF, Carver JA. (−)-Epigallocatechin-3-Gallate (EGCG) Maintains kappa-casein in its pre-fibrillar state without redirecting its aggregation pathway. J Mol Biol. 2009;392:689–700. doi: 10.1016/j.jmb.2009.07.031. [DOI] [PubMed] [Google Scholar]
- 47.Bieschke J, Russ J, Friedrich RP, Ehrnhoefer DE, Wobst H, Neugebauer K, Wanker EE. EGCG remodels mature alpha-synuclein and amyloid-beta fibrils and reduces cellular toxicity. Proc Natl Acad Sci. 2010;107:7710–7715. doi: 10.1073/pnas.0910723107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Chiti F, Stefani M, Taddei N, Ramponi G, Dobson CM. Rationalization of the effects of mutations on peptide and protein aggregation rates. Nature. 2003;424:805–808. doi: 10.1038/nature01891. [DOI] [PubMed] [Google Scholar]
- 49.Chiti F. Protein Misfolding, Aggregation, and Conformational Diseases. Springer; US: 2006. Relative importance of hydrophobicity, net charge, and secondary structure propensities in protein aggregation; pp. 43–59. [Google Scholar]
- 50.DuBay KF, Pawar AP, Chiti F, Zurdo J, Dobson CM, Vendruscolo M. Prediction of the absolute aggregation rates of amyloidogenic polypeptide chains. J Mol Biol. 2004;341:1317–1326. doi: 10.1016/j.jmb.2004.06.043. [DOI] [PubMed] [Google Scholar]
- 51.Chiti F, Webster P, Taddei N, Clark A, Stefani M, Ramponi G, Dobson CM. Designing conditions for in vitro formation of amyloid protofilaments and fibrils. Proc Natl Acad Sci. 1999;96:3590–3594. doi: 10.1073/pnas.96.7.3590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Craft DL, Wein LM, Selkoe DJ. A mathematical model of the impact of novel treatments on the Aβ burden in the Alzheimer’s brain, CSF and plasma. Bull Math Biol. 2002;64:1011–1031. doi: 10.1006/bulm.2002.0304. [DOI] [PubMed] [Google Scholar]
- 53.Simmons MK, Manjeshwar R, Agdeppa ED, Mattheyses RM, Kiehl TR, Montalto MC. A computational positron emission tomography simulation model for imaging β-Amyloid in Mice. Molecul Imag Biol. 2005;7:69–77. doi: 10.1007/s11307-005-0952-9. [DOI] [PubMed] [Google Scholar]
- 54.Gillmore JD, Hawkins PN, Pepys MB. Amyloidosis: a review of recent diagnostic and therapeutic developments. British J Haematol. 1997;99:245–256. doi: 10.1046/j.1365-2141.1997.303194.x. [DOI] [PubMed] [Google Scholar]
- 55.Kenrick FB, Wismer KL, Wyatt KS. Supersaturation of gases in liquids. J Phy Chemistry. 1924;28:1308–1315. [Google Scholar]
- 56.Liger-Belair G, Vignes-Adler M, Voisin C, Robillard B, Jeandet P. Kinetics of gas discharging in a glass of champagne: The role of nucleation sites. Langmuir. 2002;18:1294–1301. [Google Scholar]
- 57.Harper JD, Lansbury PT., Jr Models of amyloid seeding in Alzheimer’s disease and scrapie: mechanistic truths and physiological consequences of the time-dependent solubility of amyloid proteins. Ann Rev Biochem. 1997;66:385–407. doi: 10.1146/annurev.biochem.66.1.385. [DOI] [PubMed] [Google Scholar]
- 58.Yoshimura Y, Lin Y, Yagi H, Lee YH, Kitayama H, Sakurai K, So M, Ogi H, Naiki H, Goto Y. Distinguishing crystal-like amyloid fibrils and glass-like amorphous aggregates from their kinetics of formation. Proc Natl Acad Sci. 2012;109:14446–14451. doi: 10.1073/pnas.1208228109. [DOI] [PMC free article] [PubMed] [Google Scholar]