Neuromechanics of muscle synergies for posture and movement

Abstract

Recent research suggests that the nervous system controls muscles by activating flexible combinations of muscle synergies to produce a wide repertoire of movements. Muscle synergies are like building blocks, defining characteristic patterns of activation across multiple muscles that may be unique to each individual, but perform similar functions. The identification of muscle synergies has strong implications for the organization and structure of the nervous system, providing a mechanism by which task-level motor intentions are translated into detailed, low-level muscle activation patterns. Understanding the complex interplay between neural circuits and biomechanics that give rise to muscle synergies will be critical to advancing our understanding of neural control mechanisms for movement.

Introduction

How do humans and animals successfully interact with the complex and unpredictable dynamics of the natural environment? In motor control, task-level goals such as moving the hand to a target, walking through a door, or orienting the body with respect to gravity must be translated into complex muscle activation patterns that produce the movement. Studies of motor systems ranging from those of invertebrates to those of humans suggest that the nervous system uses flexible combinations of just a few muscle synergies—the elements from which complex muscle activation patterns are constructed—to produce a wide range of motor behaviors [1,2,3•,4•,5•,6]. We define a muscle synergy to be a vector specifying relative levels of muscle activation (cf. [7,8]). The absolute level of activation of each muscle synergy is presumed to be modulated by a single neural command signal. For a given motor task, several muscle synergies are activated in varying combinations to produce the motor behavior [9].

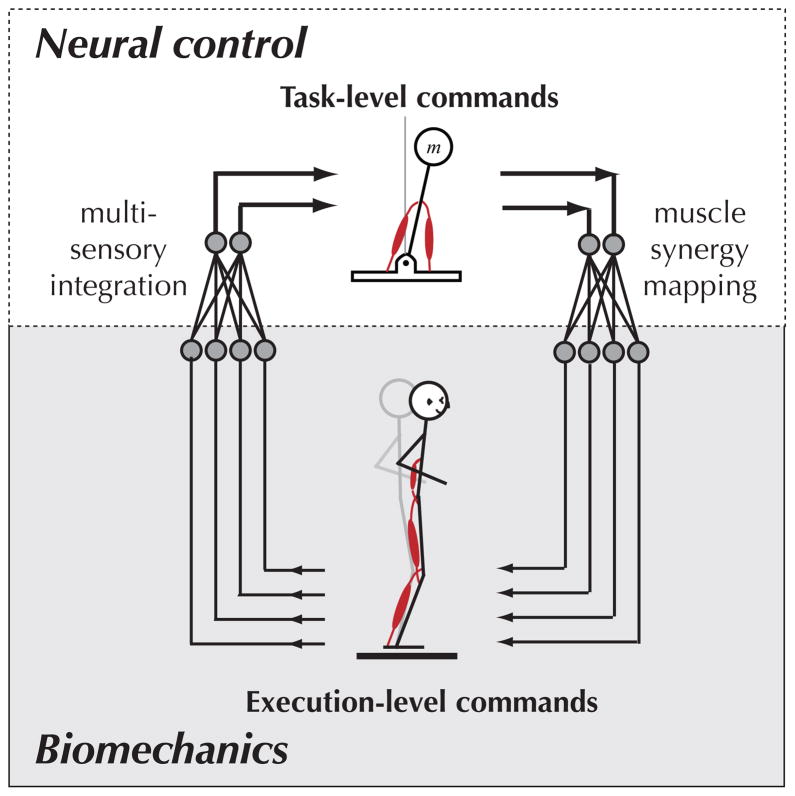
We propose that the nervous system uses muscle synergies as a set of heuristic solutions to transform task-level goals into detailed spatiotemporal patterns of muscle activation (Figure 1). Muscle synergies may therefore represent the bottom of a hierarchal neural control structure in which higher neural centers operate on increasingly conceptual variables related to task-level motor performance [10–14]. This structure mirrors the series of hierarchal transformations that occur in many sensory processing systems [15,16]. The existence of muscle synergies also implies that from among many possible motor solutions, a limited set are chosen by each individual—addressing Bernstein’s degrees-of-freedom problem [17]. Thus, at least on behaviorally short time-scales, motor patterns are constrained by the available library of muscle synergies, influencing motor performance.

Figure 1.

Muscle synergies allow task-level neural commands to be translated into execution-level muscle activation patterns. This hierarchal structure mirrors that of multisensory integration systems.

Here we review recent findings regarding the characteristics and functions of muscle synergies in a variety of motor tasks. We will focus on several open questions in the field: Do muscle synergies produce task-level functions? Are muscle synergies innate or learned? How many muscle synergies are required for task performance? We propose that appropriate neuromechanical models can help to answer these questions.

Muscle synergies

Do muscle synergies produce task-level functions, or are they an artifact of a sophisticated analysis? Recently, results from many areas have demonstrated that the activity of muscle synergies can be correlated to functional outputs related to task performance [1,7,18,19]. During standing balance control, a small set of muscle synergies can be identified that co-activate muscles throughout the limbs and trunk. For any given perturbation, one or more muscle synergies may be activated, so that their combined influences define the resulting muscle activation pattern [9]. The activity of each muscle synergy is directionally tuned, responding to specific directions of center-of-mass (CoM) motion in both voluntary [8] and reactive postural adjustments [3•,4•,20], suggesting an appealing link between muscle synergy activity and higher motor centers (e.g., [21]). In cats, muscle synergy activation has been more specifically correlated with the direction of the force vector produced by the hindlimb for postural stabilization [4•,20]. Further supporting the idea that a few descending signals determine muscle activation patterns, trial-by-trial variations in human postural control can be explained by variations in muscle synergy activation levels [3•]. Because robust muscle synergies must be identified in data sets in which the number of muscles and experimental conditions exceed the number of underlying muscle synergies, they reflect structure in the data rather than structure in the experimental design [22].

Experimental evidence also suggests that – rather than reflecting the state of local sensory or reflex networks during any particular postural task – muscle synergy function is generalized across tasks [4•,20]. When postural configuration is changed, proprioceptive information [23], H-reflex excitability [24], and even intrinsic electrical properties of spinal motoneurons [25] are altered. Despite these alterations, changes in postural responses to perturbations in a range of different postural configurations can be accounted for by modulating the activation levels of a common set of muscle synergies [4•]. Further, when there is explicit sensory loss in the visual, vestibular, or somatosensory systems, the spatial tuning characteristics of individual muscles are retained, suggesting that muscle synergy patterns are unaffected by sensory deficits [26,27]. Similarly, muscle synergies producing locomotor behaviors are largely retained after deafferentation [28]. Although sensory information appears to alter the amplitude and timing of neural commands to muscle synergies, muscle synergy patterns themselves do not appear to be affected.

Are muscle synergies innate or learned? In humans, rudimentary postural responses emerge as early as 4–5 months of age [29], suggesting that the underlying muscle synergies may be innate to some degree. It is possible that muscle synergies for postural control are encoded in cells at the level of the spinal cord [30,31] or brainstem [32•], and are similar to cortico-motoneuronal cells that coordinate hand muscles for grasp [33••,34]. However, inter-subject variations in both muscle synergy patterns and the number of muscle synergies suggest that muscle synergies are shaped by adaptive processes. If this is the case, the morphology and experience of each individual may interact in unexpected ways over time [35], resulting in a unique set of muscle synergy patterns. More subtly, these adaptive processes themselves may vary depending on context [36•,37]. It is therefore reasonable to expect that adaptation may occur differently – and at different rates – for muscle synergy patterns and for descending commands [38•]. Fundamentally, mechanics dictates that responses to postural perturbations across subjects must be similar in terms of kinetic and kinematic variables (cf. [39]). Accordingly, in cats, the directional tuning and force outputs of each muscle synergy are consistent across animals, but the specific muscular patterns of each muscle synergy vary considerably across animals [4•]. Despite these variations, the particular muscle synergy pattern chosen by a subject – whether cat or human – is stable across days and does not appear to be rapidly modified. In contrast, levels of muscle synergy activation, which we presume to reflect descending neural commands, change both across and within experimental conditions [3•,4•].

Finally, how many muscle synergies are required for task performance? Clinically, muscle synergies have been associated with constraints on movement in motor deficit, for example the “pathological synergies” associated with stroke [40,41]. How can we reconcile this conception of muscle synergies with the above studies demonstrating healthy subjects using muscle synergies as a flexible, dextrous strategy? We hypothesize that even in healthy subjects, motor patterns are in fact constrained by the available library of muscle synergies, limiting motor performance to well within the boundaries imposed by musculoskeletal mechanics (cf. [33••,42]). Perhaps then, the difference between some conditions of motor deficit and motor skill is simply a matter of the number of available muscle synergies and the appropriateness of those muscle synergies [43,44].

Neuromechanical modeling

Neuromechanical modeling studies [45] may help resolve these and other pertinent questions regarding muscle synergies. In this section we will outline the advantages of this integrative approach.

Anatomically-detailed biomechanical models are critical for estimating muscle synergy function. Because of interactions between musculoskeletal elements, the function of any single muscle or muscle synergy cannot be examined in isolation. As all muscles accelerate joints they do not cross, proximal and distal muscles must be co-activated to produce stable task function [46–48,49•]. This idea is strikingly apparent when one considers animals without obvious rigid structure (e.g., [50•]).

However, biomechanical models in themselves are insufficient to reveal neural control mechanisms, but rather provide a landscape of possible solutions available to the nervous system. In most natural behaviors, task-level goals can be equivalently achieved with different kinetic or kinematic strategies [51–53], which can themselves be equivalently achieved with different spatial and temporal patterns of muscle activation [54•,55,56]. Therefore, biomechanical models do not uniquely determine muscle activation patterns, nor do they predict muscle synergies, but rather they delineate the large “solution space” afforded by the musculoskeletal system for task performance.

What computations might determine the way the nervous system coordinates muscles? One possibility is that the nervous system explicitly encodes an appropriate transformation function (e.g., an “inverse internal model” [57]), perhaps selected to optimize various performance criteria [56,58•,59,60]. These explanations produce good estimates of experimental measures, generally describing mean neural behaviors without estimating variations from that mean. In general, such models do not directly address how such computations might be inplemented, but instead assume that the nervous system is unconstrained in its plasticity [61].

Neural models that incorporate relevant properties and constraints of neural processing are also necessary to understand how muscle synergies might be encoded in the nervous system. Information representation in the nervous system may be limited by metabolic constraints, making some computational structures more favorable than others [16,62•]. Such “sparse” representations appear to encode explicit features in the environment in an efficient manner [16]. Additionally, the nervous system adapts through statistical learning processes [36•,37,63], so that computational structures may reflect the prior experience of the individual. In turn, conservative mechanisms may limit the context and extent of adaptation [36•,64].

Although the constraints of the nervous system are important, the solution space afforded by the nervous system is still very large. In neural systems, the same network can be modified to produce a variety of outputs [50•,65], which in turn can be equivalently produced by a many different parameter states [66,67]. Therefore, neural models are also insufficient to specify muscle synergies, providing only a landscape of possible motor output patterns.

We propose that muscle synergies emerge from the interacting constraints and features of the nervous and musculoskeletal systems. Our rationale is supported by computational studies of motor cortex topography demonstrating that functionally-organized regions of the cortex may arise from interactions between the biomechanical characteristics of the behavioral repertoire and the biases in the nervous system towards co-localizing neurons that process similar information [68,69•,70]. As an example relevant to muscle synergies, consider the energetic constraints on the musculoskeletal and nervous systems during locomotion. Movement patterns are energetically efficient in a mechanical sense when joint motions are functionally immobilized or linearly correlated (e.g. “inverted pendulum,” or “spring-mass” dynamics in locomotion [71–74]). Simultaneously, energetic efficiency in neural systems — limiting the number of neurons dedicated to encode task performance — may favor piecewise-linear representations of complex elements [16,52]. Thus the combined neural and mechanical energetic pressures may give rise to a motor control strategy of activating linear combinations of muscle synergies that coordinate the musculoskeletal system to act in low-dimensional movement patterns [33••,67].

Muscle synergies may allow higher centers in the nervous system to encode task-level variables, perhaps enabling faster adaptation to environmental demands. In postural control a few variables encoding overall body motion are sufficient to specify muscle synergy activation levels over the time-course of a postural response [54••], eliminating the need to actively control lower-level variables, for example individual joints. This type of dimensional reduction in the neuromechanical system may also explain why simple biomechanical models can predict complex motor behaviors [71–74], as well as compensatory strategies in motor deficit [54••,75•]. But, it is important to note that these low-dimensional and linear behaviors arise from specific relationships between many nonlinear components within the neural and musculoskeletal systems [16,55,67,76••], and do not imply that the systems themselves are linear. Muscle synergies may reflect a sparse code for motor tasks, whereby higher centers can rapidly reconfigure the coordination of task-level commands to muscle synergies, which in turn coordinate specific elements in the periphery that produce functional behaviors [67,77]. Muscle synergies therefore represent a solution to an inverse “binding problem” typical of sensory systems by encoding functional, task-relevant muscle coordination patterns [78]. Thus, muscle synergies may be stable over short-term motor adaptation, but over longer time scales, muscle synergies themselves may also change [38•]. Because of the large solution space of muscle synergies sufficiently near the energetically optimal operating regions defined by simple biomechanical models, a cascade of ancillary factors may influence the specific muscle synergy patterns within each individual [79].

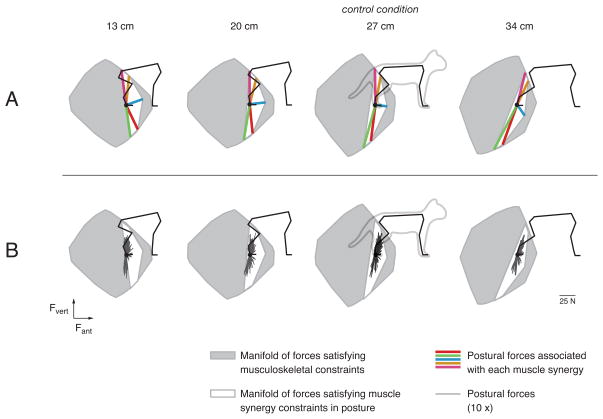
Neuromechanical models can be a practical way to estimate the degree to which motor patterns are constrained by the available library of muscle synergies and whether these constraints influence motor performance. Due to adaptive processes, in statistically-likely tasks motor performance using muscle synergies can approximate that of an optimal controller [10,46,80•]. However, in statistically-unlikely conditions, this approximation may be degraded (cf. [52]). As an example, using a neuromechanical model of the cat hindlimb [81•] we demonstrated that muscle synergies used for postural control in the cat restrict the force-production capability of the limb (Figure 2, [81•]), but may also reduce moments about the CoM when the cat stands in a postural configuration approximating its natural stance. However, when the cat is required to assume postural configurations away from the “preferred” condition, postural forces rotate with the sagittal limb axis, creating large moments about the CoM. This rotation is not imposed by biomechanical limitations, but appears to be a consequence of using identical muscle synergies in disparate postural configurations. Similarly, neuromechanical models of both finger force generation and pedaling in humans demonstrate that muscle activation patterns corresponding to maximal task performance appear to be retained at sub-maximal levels [46,82], possibly in order to achieve a range of related behaviors using the smallest number of muscle synergies. These studies suggest that from the perspective of the nervous system, there may be some “cost” associated with increasing the number of muscle synergies; however, this has yet to be explicitly compared to that of the sub-optimal performance that may arise as a consequence of using fewer muscle synergies.

Figure 2.

The force-production capability of the cat hindlimb is restricted when an identical set of muscle synergies is used for balance control in different postural configurations (adapted from [81•]). A: The gray polygons represent the manifold of possible endpoint forces in a neuromechanical model of the cat hindlimb, given musculoskeletal constraints. From left to right, postural configuration is altered by increasing the “stance distance”, or the anterior-posterior distance between the feet. The most natural, “preferred” postural configuration in the third column is denoted by the cartoon cat. Colored lines denote the force vectors associated with each experimentally-observed muscle synergy. These synergy force vectors rotate with the limb axis as postural configuration changes. The white polygons represent the restricted manifold of possible endpoint forces when the experimentally-identified muscle synergies are used at all postures. B: Manifolds from A are overlaid with recorded postural forces. The “synergy-limited” manifolds predict the systematic rotation of postural forces as stance distance increases.

Finally, neuromechanical models may help explain the redundancy that exists between neural and biomechanical motor control strategies. Biomechanical mechanisms may perform computation typically attributed to active neural control [74,83•]. This idea has been linked to Bernstein’s [17] concept of “preparing the periphery” [50]. In posture, stabilization of the body occurs with equal frequency across individuals through feedforward activation of muscles or through sensory feedback control [84•]. These strategies predict qualitatively different muscle synergy patterns. In the first, a muscle pattern is selected to increase the stiffness of the system, rejecting perturbations using biomechanical properties of the musculature. In the second, a muscle pattern is selected to increase the compliance of the system, to facilitate the effectiveness of the active response (NE Bunderson, TJ Burkholder, LH Ting, American Society of Biomechanics, 2007, also J Biomech in review). The decision to use any particular balance of these two strategies within each individual may be a heuristic process based on experience. Similarly, any particular muscle synergy pattern may represent a unique coordination solution that emerges from complex, multifaceted interactions between the components of the neuromechanical system. Future work investigating the robustness, flexibility, and emergence of muscle synergies depends upon the development of neuromechanical models as well as evaluation techniques to quantify the interactions of components within the models [76••].

Abbreviations

CoM

center of mass