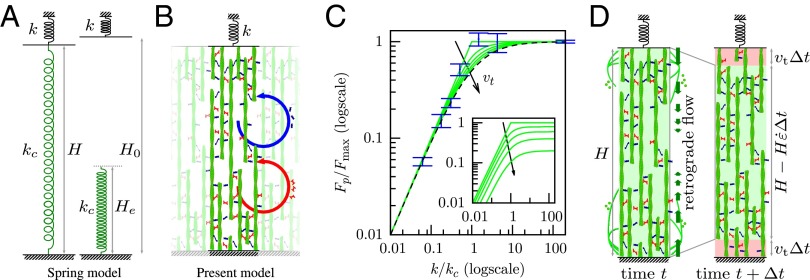
Fig. 3.

A 1D simplification of the 3D model preserves the essential mechanisms and results. (A) The spring model with spring stiffness $k_c$ and rest length $L_e$ used elsewhere in the literature with which this model is compared (SI Text, S4.2). (B) Sketch of the 1D model. Actin filaments (green) are bound together by myosin (red) and other cross-linkers (blue), forming a structure of elastic modulus E. Cross-linkers and myosin unbind at a fixed frequency, which is at the origin of the viscoelastic behavior (SI Text, S2), and rebind so that their average number per filament unit length remains constant in time. In addition, myosins perform power strokes at a fixed frequency. The resulting rheology is sketched in Fig. S5C. (C) Equilibrium state of models and cells as a function of microplate stiffness k normalized by critical stiffness $k_c$ and maximum force $F_{\max }$ in each case. Blue, experimental results plotted with $k_c={\sigma }_{\text{a}}/\left(L_0+4{\tau }_{\alpha }{v}_{\text{t}}\right)=41$ nN/$\mathrm{\mu }\text{m}$ (no adjustment) (SI Text, S3.6); dashes, tension of the spring model; green, tension calculated in the 1D model for different values of the speed of treadmilling $v_{\text{t}}$. The stiffness dependence of force in experiments is well-matched by both the spring model and the 1D model. (Inset) Tension calculated in the 1D model for different values of the speed of treadmilling $v_{\text{t}}$ and normalized by $F_{\max }$ in the absence of treadmilling $v_{\text{t}}=0$: treadmilling reduces the force transmitted to the microplates. (D) A dynamic equilibrium is attained when the retrograde flow exactly balances the speed of polymerization at the boundaries (here, sketched in the 1D model geometry).