Figure 5. A random 91 knot and its disk matrix.
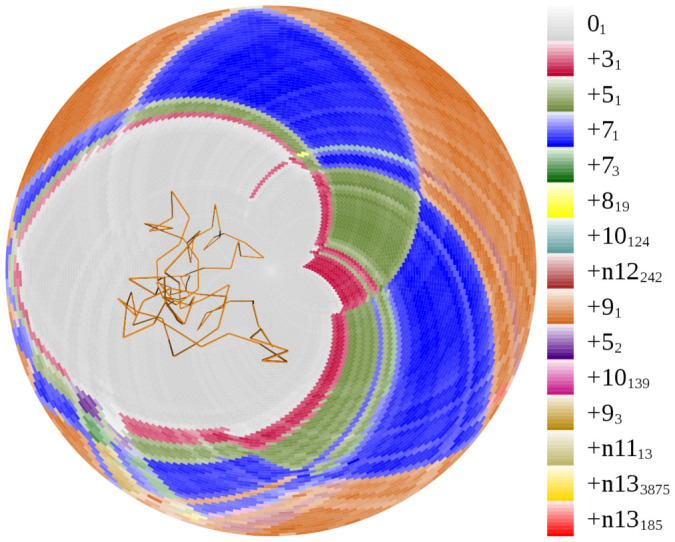
Notice the presence of the predecessors 71, 51 and 31 as first, second, and third-generation subknots, respectively. Notice also the presence of several more complicated subknots, which consume a small amount of the area of the disk matrix. For the knot types with more than 10 crossings, we use the Dowker-Thistlethwaite notation where the leading letter (n or a) tells whether the knot type is non-alternating or alternating, respectively, and the knot types are indexed within the non-alternating and alternating classes.
