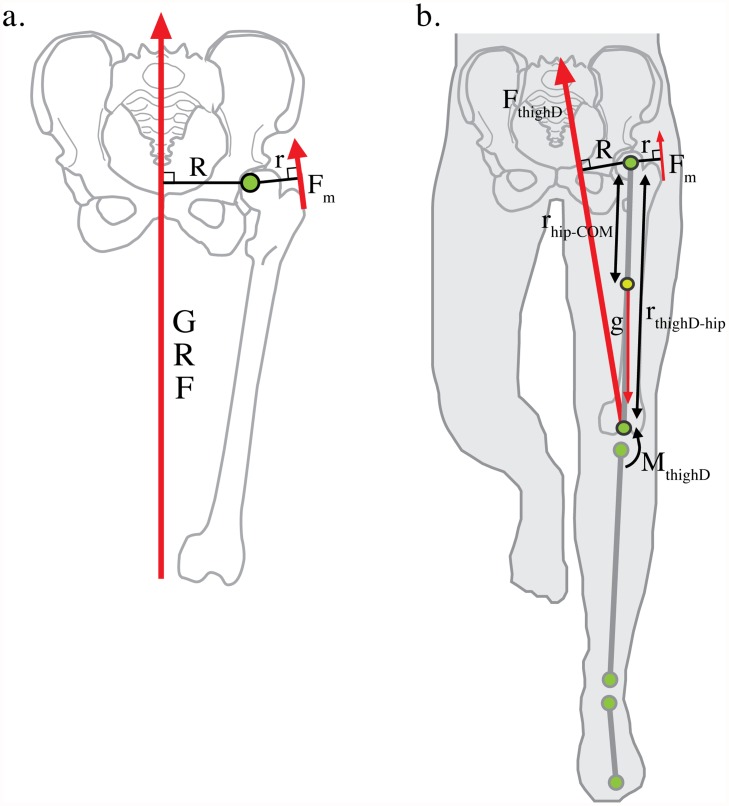
Fig 1. Static and dynamic models of hip abductor force production.

a. The standard static biomechanical model of hip abductor force production assumes the ground reaction force vector (GRF) passes nearly vertically through the body center of mass during locomotion. The effective mechanical advantage (EMA) of the hip abductor muscles is defined as r/R, where r is the abductor muscle moment arm and R is the moment arm of the GRF vector. Hip abductor force (F _m) is equal the multiple of GRF and 1/EMA. A narrow pelvis is thought to reduce locomotor cost by decreasing R and hip abductor force production, but this may increase the likelihood of cephalopelvic disproportion (CPD) by narrowing the maternal birth canal. b. Inverse dynamics models the lower extremity as a series of linked-segments in which the foot, shank and thigh each act as rigid bodies interacting at frictionless joints [23,24]. The net internal hip moment is equal to the thigh moment of inertia times its angular acceleration, minus the distal thigh moment (M _thighD), minus the cross-product of the positional vector of hip relative to the thigh center of mass (r _hip-COM) and gravity (g), minus the external moment acting on the thigh defined as the cross product of the positional vector of the distal thigh segment relative to the hip (r _thighD-hip) and the force vector acting on the distal thigh (F _thighD). R can then be measured dynamically as the perpendicular distance from the hip joint center to F _thighD (see Methods). If the predictions of the static model and the obstetrical dilemma hold, R measured dynamically will be nearly equal to half- biacetabular width.