Figure 2. Kinetic defect observed on addition of second and third lysine residues in iterated lysine stretch.
(A) Example eTLC displaying the E. coli translation products of a AUG-(AAA)5-UAA message. The ± poles of the electrophoretic TLC are indicated. MK4 and MK5 products (and those with greater numbers of lysine) are difficult to resolve in this system but the other products are easily visualized. (B) Kinetic scheme for rate constants of sequential lysine additions to peptide chain. (C) Bar graph displaying rate constants for the addition of individual lysines to a variety of messages: MKFK-Stop (gray), MKA5-Stop (blue), MKG5-Stop (black), and MFK (gray).
Figure 2—figure supplement 1. Ribosomes stall while adding a second lysine.
Toeprinting assays were performed with constructs containing 1–12 consecutive lysines inserted (either AAG and AAA codons). Assays were performed in the presence and absence of thiostrepton to mark ribosomes on the initiating AUG codon. Sequences on which toeprints appear are highlighted in red.
Figure 2—figure supplement 2. Modeling of rate constants in Mathematica.
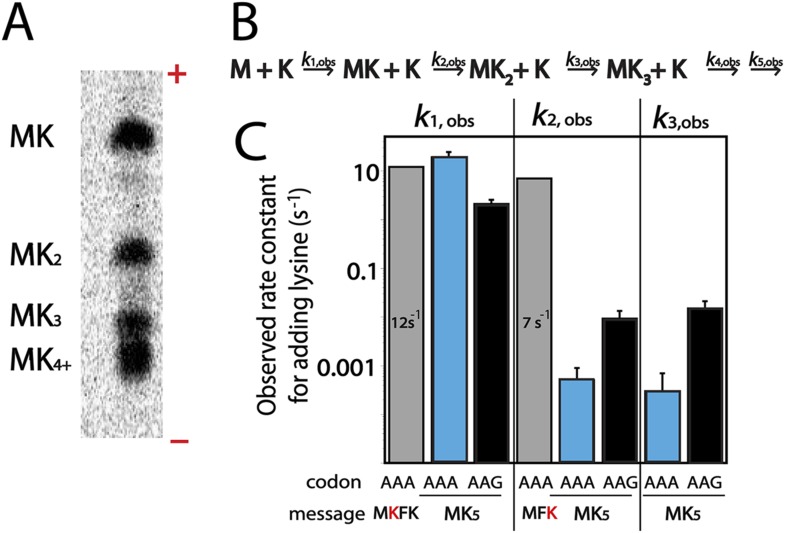
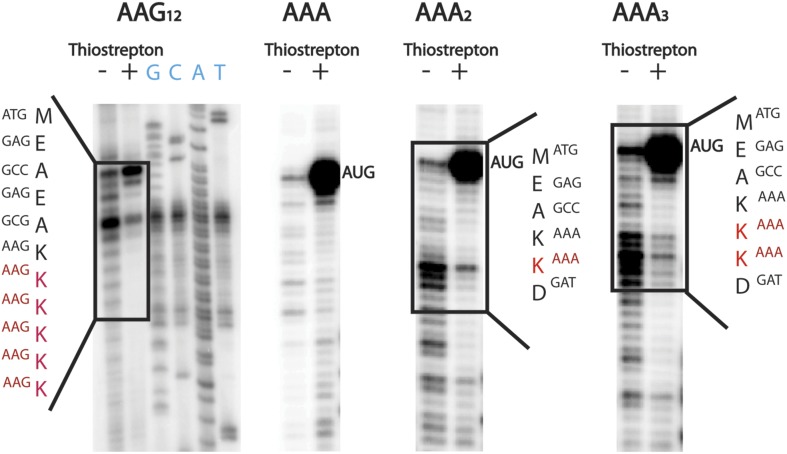
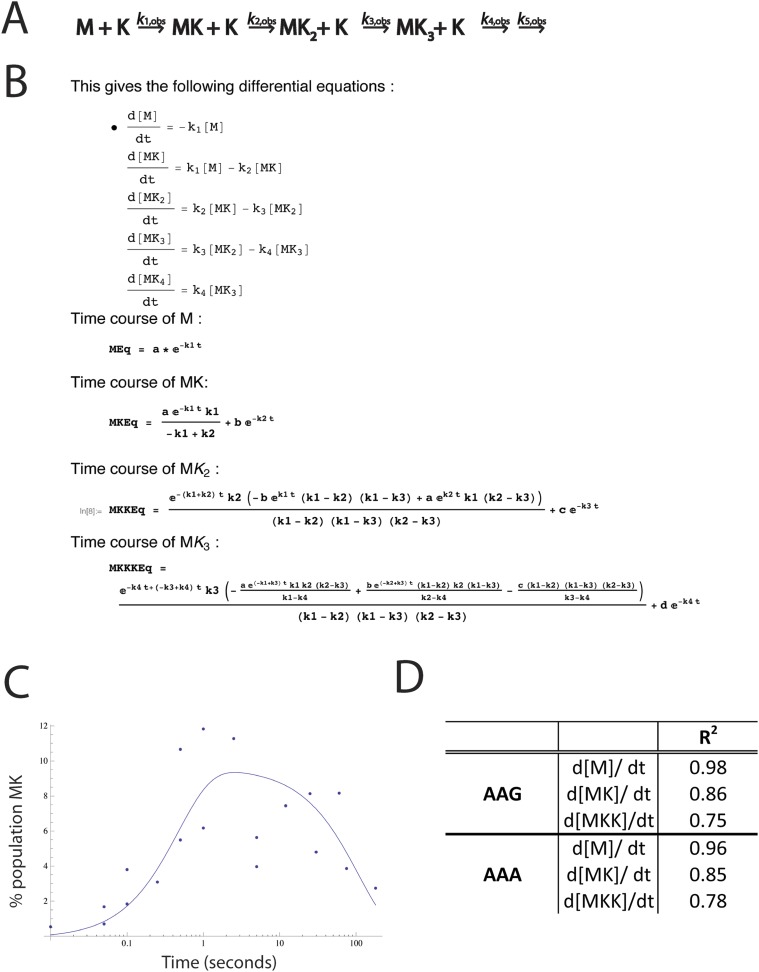
(A) Kinetic scheme used to model the rate constants of sequential lysine additions to the peptide chain (same as Figure 2A). We also attempted to model with peptidyl-tRNA drop-off rates included. Inserting peptidyl-tRNA drop-off into our model decreases the quality of fits, and returns rates of drop-off small enough that they are inconsequential relative to the time scale of the reaction. (B) The top panel displays the differential equations used to solve for each rate constant. The bottom panels display the mathematical solutions for the differential equations. These solutions were used to perform modeling and fit the data. The fits were performed both iteratively (e.g., we solved for k1 by fitting the plots measuring the disappearance of M, then input that value into the equation describing the appearance of MK to solve for k2) and by letting all of the values float for each data set. In both cases, the rate constants modeled were essentially the same, indicating that the first lysine is added quickly (k1), and subsequent lysines (k2, k3) are added more slowly. (C) An example fit in Mathematica showing time course for the formation and depletion of MK on a message with AAG codons. This time course, for example, was used to model the k2 value. (D) R2 values for the fits for the appearance and disappearance of each species used to model rate constants.