Fig. 2.

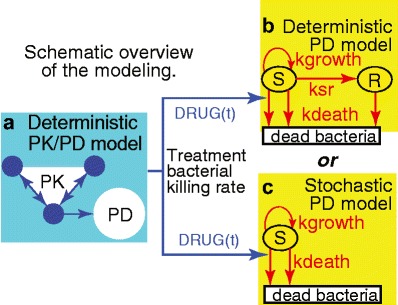
Abbreviated synopsis of the modeling. a As input for deterministic or stochastic PD models of CFU growth and death one needs a rate for the killing of cycling bacteria by gentamicin. This rate, the function DRUG(t), was estimated by using published PK/PD mathematical models, consisting of a standard 3-compartment PK model (small circles), and then a deterministic PD calculation (large circle) accounting for the fact that CFU develop reversible, transient, “adaptive” gentamicin drug resistance in response to dosing. DRUG(t) is a non-linear function of the free drug concentration calculated from the PK model. b Additional PD calculations are needed to estimate, using the published deterministic model, the total number, s(t), of bacteria per patient in the compartment S for cycling CFU, and the number r(t) of possible “resting” (quiescent) bacteria in compartment R, which is initially empty, i.e., r(0) = 0. Arrows indicate bacterial cell population dynamical processes and their labels are transition rates. For example, ksr, which is time and density dependent, is the rate at which cycling bacteria become quiescent. According to the model, ksr becomes substantial only if the total number of bacteria grows to about 100 times the number present at birth; until then the decrease of cycling bacteria due to onset of quiescence is predicted to be negligible. c The present paper emphasizes a stochastic mathematical model of the eradication probability E(t) that s(t) = 0. In the stochastic calculation: (i) The number s is considered to jump from integer to integer as time increases. For reasons explained in the “Results” section, it is possible to use a simplified model which has no R compartment. (ii) Jump probabilities are determined by rates: for treatment killing (downward arrow at left) with per-cell jump probability DRUG(t) h⁻¹; for background killing (other downward arrow) with per-cell jump probability kdeath h⁻¹; and for bacterial fission with per-cell jump probability kgrowth h⁻¹. (iii) E(t) is the probability that at some time between 0 and t, s has jumped from 1 to 0, whereupon, according to the model, it remains 0. Thus, E(t) always increases as time increases. None of the calculations attempt to take into account irreversible gentamicin resistance or neonate immune system assistance to gentamicin treatment