Abstract
The calibration and performance of the opposite-side flavour tagging algorithms used for the measurements of time-dependent asymmetries at the LHCb experiment are described. The algorithms have been developed using simulated events and optimized and calibrated with B+→J/ψK+, B0→J/ψK∗0 and B0→D∗−μ+νμ decay modes with 0.37 fb−1 of data collected in pp collisions at 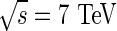 during the 2011 physics run. The opposite-side tagging power is determined in the B+→J/ψK+ channel to be (2.10±0.08±0.24) %, where the first uncertainty is statistical and the second is systematic.
during the 2011 physics run. The opposite-side tagging power is determined in the B+→J/ψK+ channel to be (2.10±0.08±0.24) %, where the first uncertainty is statistical and the second is systematic.
Introduction
The identification of the flavour of reconstructed B0 and 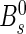 mesons at production is necessary for the measurements of oscillations and time-dependent CP asymmetries. This procedure is known as flavour tagging and is performed at LHCb by means of several algorithms.
mesons at production is necessary for the measurements of oscillations and time-dependent CP asymmetries. This procedure is known as flavour tagging and is performed at LHCb by means of several algorithms.
Opposite-side (OS) tagging algorithms rely on the pair production of b and 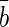 quarks and infer the flavour of a given B meson (signal B) from the identification of the flavour of the other b hadron (tagging B).1,2 The algorithms use the charge of the lepton (μ, e) from semileptonic b decays, the charge of the kaon from the b→c→s decay chain or the charge of the inclusive secondary vertex reconstructed from b-hadron decay products. All these methods have an intrinsic dilution on the tagging decision, for example due to the possibility of flavour oscillations of the tagging B. This paper describes the optimization and calibration of the OS tagging algorithms which are performed with the data used for the first measurements performed by LHCb on
quarks and infer the flavour of a given B meson (signal B) from the identification of the flavour of the other b hadron (tagging B).1,2 The algorithms use the charge of the lepton (μ, e) from semileptonic b decays, the charge of the kaon from the b→c→s decay chain or the charge of the inclusive secondary vertex reconstructed from b-hadron decay products. All these methods have an intrinsic dilution on the tagging decision, for example due to the possibility of flavour oscillations of the tagging B. This paper describes the optimization and calibration of the OS tagging algorithms which are performed with the data used for the first measurements performed by LHCb on 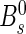 mixing and time-dependent CP violation [1–3].
mixing and time-dependent CP violation [1–3].
Additional tagging power can be derived from same-side tagging algorithms which determine the flavour of the signal B by exploiting its correlation with particles produced in the hadronization process. The use of these algorithms at LHCb will be described in a forthcoming publication. The use of flavour tagging in previous experiments at hadron colliders is described in Refs. [4, 5].
The sensitivity of a measured CP asymmetry is directly related to the effective tagging efficiency εeff, or tagging power. The tagging power represents the effective statistical reduction of the sample size, and is defined as
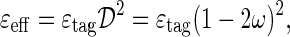 |
1 |
where εtag is the tagging efficiency, ω is the mistag fraction and 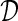 is the dilution. The tagging efficiency and the mistag fraction are defined as
is the dilution. The tagging efficiency and the mistag fraction are defined as
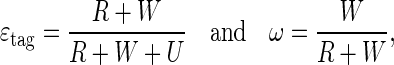 |
2 |
where R, W, U are the number of correctly tagged, incorrectly tagged and untagged events, respectively.
The mistag fraction can be measured in data using flavour-specific decay channels, i.e. those decays where the final state particles uniquely define the quark/antiquark content of the signal B. In this paper, the decay channels B+→J/ψK+, B0→J/ψK∗0 and B0→D∗−μ+νμ are used. For charged mesons, the mistag fraction is obtained by directly comparing the tagging decision with the flavour of the signal B, while for neutral mesons it is obtained by fitting the B0 flavour oscillation as a function of the decay time.
The probability of a given tag decision to be correct is estimated from the kinematic properties of the tagging particle and the event itself by means of a neural network trained on Monte Carlo (MC) simulated events to identify the correct flavour of the signal B. When more than one tagging algorithm gives a response for an event, the probabilities provided by each algorithm are combined into a single probability and the decisions are combined into a single decision. The combined probability can be exploited on an event-by-event basis to assign larger weights to events with low mistag probability and thus to increase the overall significance of an asymmetry measurement. In order to get the best combination and a reliable estimate of the event weight, the calculated probabilities are calibrated on data. The default calibration parameters are extracted from the B+→J/ψK+ channel. The other two flavour-specific channels are used to perform independent checks of the calibration procedure.
The LHCb detector and the data sample
The LHCb detector [6] is a single-arm forward spectrometer which measures CP violation and rare decays of hadrons containing b and c quarks. A vertex detector (VELO) determines with high precision the positions of the primary and secondary vertices as well as the impact parameter (IP) of the reconstructed tracks with respect to the primary vertex. The tracking system also includes a silicon strip detector located in front of a dipole magnet with integrated field about 4 Tm, and a combination of silicon strip detectors and straw drift chambers placed behind the magnet. Charged hadron identification is achieved through two ring-imaging Cherenkov (RICH) detectors. The calorimeter system consists of a preshower detector, a scintillator pad detector, an electromagnetic calorimeter and a hadronic calorimeter. It identifies high transverse energy hadron, electron and photon candidates and provides information for the trigger. Five muon stations composed of multi-wire proportional chambers and triple-GEMs (gas electron multipliers) provide fast information for the trigger and muon identification capability.
The LHCb trigger consists of two levels. The first, hardware-based, level selects leptons and hadrons with high transverse momentum, using the calorimeters and the muon detectors. The hardware trigger is followed by a software High Level Trigger (HLT), subdivided into two stages that use the information from all parts of the detector. The first stage performs a partial reconstruction of the event, reducing the rate further and allowing the next stage to fully reconstruct and to select the events for storage up to a rate of 3 kHz.
The majority of the events considered in this paper were triggered by a single hadron or muon track with large momentum, transverse momentum and IP. In the HLT, the channels with a J/ψ meson in the final state were selected by a dedicated di-muon decision that does not apply any requirement on the IP of the muons.
The data used in this paper were taken between March and June 2011 and correspond to an integrated luminosity of 0.37 fb−1. The polarity of the LHCb magnet was reversed several times during the data taking period in order to minimize systematic biases due to possible detector asymmetries.
Flavour tagging algorithms
Opposite-side tagging uses the identification of electrons, muons or kaons that are attributed to the other b hadron in the event. It also uses the charge of tracks consistent with coming from a secondary vertex not associated with either the primary or the signal B vertex. These taggers are called electron, muon, kaon and vertex charge taggers, respectively. The tagging algorithms were developed and studied using simulated events. Subsequently, the criteria to select the tagging particles and to reconstruct the vertex charge are re-tuned, using the B+→J/ψK+ and the B0→D∗−μ+νμ control channels. An iterative procedure is used to find the selection criteria which maximize the tagging power εeff.
Only charged particles reconstructed with a good quality of the track fit are used. In order to reject poorly reconstructed tracks, the track is required to have a polar angle with respect to the beamline larger than 12 mrad and a momentum larger than 2 GeV/c. Moreover, in order to avoid possible duplications of the signal tracks, the selected particles are required to be outside a cone of 5 mrad formed around any daughter of the signal B. To reject tracks coming from other primary interactions in the same bunch crossing, the impact parameter significance with respect to these pile-up (PU) vertices, 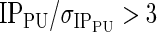 , is required.
, is required.
Single-particle taggers
The tagging particles are selected exploiting the properties of the b-hadron decay. A large impact parameter significance with respect to the primary vertex (IP/σIP) and a large transverse momentum pT are required. Furthermore, particle identification cuts are used to define each tagger based on the information from the RICH, calorimeter and muon systems. For this purpose, the differences between the logarithm of the likelihood for the muon, electron, kaon or proton and the pion hypotheses (referred as DLLμ−π, DLLe−π, DLLK−π and DLLp−π) are used. The detailed list of selection criteria is reported in Table 1. Additional criteria are used to identify the leptons. Muons are required not to share hits in the muon chambers with other tracks, in order to avoid mis-identification of tracks which are close to the real muon. Electrons are required to be below a certain threshold in the ionization charge deposited in the silicon layers of the VELO, in order to reduce the number of candidates coming from photon conversions close to the interaction point. An additional cut on the ratio of the particle energy E as measured in the electromagnetic calorimeter and the momentum p of the candidate electron measured with the tracking system, E/p>0.6, is applied.
Table 1.
Selection criteria for the OS muon, electron and kaon taggers
| Tagger | min p T [GeV/c] | min p [GeV/c] | min (IP/σ IP) | Particle identification cuts | min (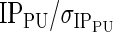 ) ) |
|---|---|---|---|---|---|
| μ | 1.2 | 2.0 | – | DLLμ−π>2.5 | 3.0 |
| e | 1.0 | 2.0 | 2.0 | DLLe−π>4.0 | 3.0 |
| K | 0.8 | 5.9 | 4.0 | DLLK−π>6.5 | 4.7 |
| DLLK−p>−3.5 |
In the case of multiple candidates from the same tagging algorithm, the single-particle tagger with the highest pT is chosen and its charge is used to define the flavour of the signal B.
Vertex charge tagger
The vertex charge tagger is based on the inclusive reconstruction of a secondary vertex corresponding to the decay of the tagging B. The vertex reconstruction consists of building a composite candidate from two tracks with a transverse momentum pT>0.15 GeV/c and IP/σIP>2.5. The pion mass is attributed to the tracks. Moreover, good quality of the vertex reconstruction is required and track pairs with an invariant mass compatible with a 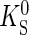 meson are excluded. For each reconstructed candidate the probability that it originates from a b-hadron decay is estimated from the quality of the vertex fit as well as from the geometric and kinematic properties. Among the possible candidates the one with the highest probability is used. Tracks that are compatible with coming from the two track vertex but do not originate from the primary vertex are added to form the final candidate. Additional requirements are applied to the tracks associated to the reconstructed secondary vertex: total momentum > 10 GeV/c, total pT>1.5 GeV/c, total invariant mass > 0.5 GeV/c2 and the sum of IP/σIP of all tracks > 10.
meson are excluded. For each reconstructed candidate the probability that it originates from a b-hadron decay is estimated from the quality of the vertex fit as well as from the geometric and kinematic properties. Among the possible candidates the one with the highest probability is used. Tracks that are compatible with coming from the two track vertex but do not originate from the primary vertex are added to form the final candidate. Additional requirements are applied to the tracks associated to the reconstructed secondary vertex: total momentum > 10 GeV/c, total pT>1.5 GeV/c, total invariant mass > 0.5 GeV/c2 and the sum of IP/σIP of all tracks > 10.
Finally, the charge of the tagging B is calculated as the sum of the charges Qi of all the tracks associated to the vertex, weighted with their transverse momentum to the power κ
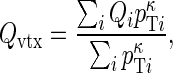 |
3 |
where the value κ=0.4 optimizes the tagging power. Events with |Qvtx|<0.275 are rejected as untagged.
Mistag probabilities and combination of taggers
For each tagger i, the probability ηi of the tag decision to be wrong is estimated by using properties of the tagger and of the event itself. This mistag probability is evaluated by means of a neural network trained on simulated B+→J/ψK+ events to identify the correct flavour of the signal B and subsequently calibrated on data as explained in Sect. 5.
The inputs to each of the neural networks are the signal B transverse momentum, the number of pile-up vertices, the number of tracks preselected as tagging candidates and various geometrical and kinematic properties of the tagging particle (p, pT and IP/σIP of the particle), or of the tracks associated to the secondary vertex (the average values of pT, of IP, the reconstructed invariant mass and the absolute value of the vertex charge).
If there is more than one tagger available per event, the decisions provided by all available taggers are combined into a final decision on the initial flavour of the signal B. The combined probability P(b) that the meson contains a b-quark is calculated as
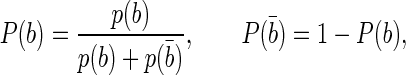 |
4 |
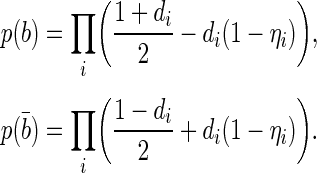
where
 |
5 |
Here, di is the decision taken by the i-th tagger based on the charge of the particle with the convention di=1(−1) for the signal B containing a 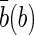 quark and ηi the corresponding predicted mistag probability. The combined tagging decision and the corresponding mistag probability are d=−1 and η=1−P(b) if
quark and ηi the corresponding predicted mistag probability. The combined tagging decision and the corresponding mistag probability are d=−1 and η=1−P(b) if 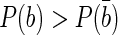 , otherwise d=+1 and
, otherwise d=+1 and 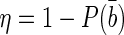 .
.
The contribution of taggers with a poor tagging power is limited by requiring the mistag probabilities of the kaon and the vertex charge to be less than 0.46.
Due to the correlation among taggers, which is neglected in (5), the combined probability is slightly overestimated. The largest correlation occurs between the vertex charge tagger and the other OS taggers, since the secondary vertex may include one of these particles. To correct for this overestimation, the combined OS probability is calibrated on data, as described in Sect. 5.
Control channels
The flavour-specific B decay modes B+→J/ψK+, B0→J/ψK∗0 and B0→D∗−μ+νμ are used for the tagging analysis. All three channels are useful to optimize the performance of the OS tagging algorithm and to calibrate the mistag probability. The first two channels are chosen as representative control channels for the decays 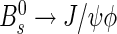 and
and 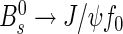 , which are used for the measurement of the
, which are used for the measurement of the 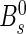 mixing phase ϕs [2, 3], and the last channel allows detailed studies given the high event yield of the semileptonic decay mode. All B decay modes with a J/ψ meson in the final state share the same trigger selection and common offline selection criteria, which ensures a similar performance of the tagging algorithms. Two trigger selections are considered, with or without requirements on the IP of the tracks. They are labeled “lifetime biased” and “lifetime unbiased”, respectively.
mixing phase ϕs [2, 3], and the last channel allows detailed studies given the high event yield of the semileptonic decay mode. All B decay modes with a J/ψ meson in the final state share the same trigger selection and common offline selection criteria, which ensures a similar performance of the tagging algorithms. Two trigger selections are considered, with or without requirements on the IP of the tracks. They are labeled “lifetime biased” and “lifetime unbiased”, respectively.
Analysis of the B+→J/ψK+ channel
The B+→J/ψK+ candidates are selected by combining J/ψ→μ+μ− and K+ candidates. The J/ψ mesons are selected by combining two muons with transverse momenta pT>0.5 GeV/c that form a common vertex of good quality and have an invariant mass in the range 3030–3150 MeV/c2. The K+ candidates are required to have transverse momenta pT>1 GeV/c and momenta p>10 GeV/c and to form a common vertex of good quality with the J/ψ candidate with a resulting invariant mass in a window ±90 MeV/c2 around the B+ mass. Additional requirements on the particle identification of muons and kaons are applied to suppress the background contamination. To enhance the sample of signal events and reduce the dominant background contamination from prompt J/ψ mesons combined with random kaons, only the events with a reconstructed decay time of the B+ candidate t>0.3 ps are selected. The decay time t and the invariant mass m of the B+ meson are extracted from a vertex fit that includes a constraint on the associated primary vertex, and a constraint on the J/ψ mass for the evaluation of the J/ψK invariant mass. In case of multiple B candidates per event, only the one with the smallest vertex fit χ2 is considered.
The signal events are statistically disentangled from the background, which is dominated by partially reconstructed b-hadron decays to J/ψK+X (where X represents any other particle in the decay), by means of an unbinned maximum likelihood fit to the reconstructed B+ mass and decay time. In total ∼85 000 signal events are selected with a background to signal ratio B/S∼0.035, calculated in a window of ±40 MeV/c2 centered around the B+ mass. The mass fit model is based on a double Gaussian distribution peaking at the B+ mass for the signal and an exponential distribution for the background. The time distributions of both the signal and the background are assumed to be exponential, with separate decay constants. The fraction of right, wrong or untagged events in the sample is determined according to a probability density function (PDF), 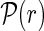 , that depends on the tagging response r, defined by
, that depends on the tagging response r, defined by
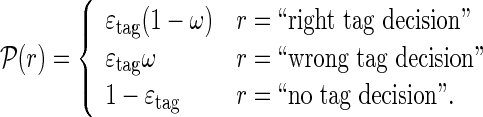 |
6 |
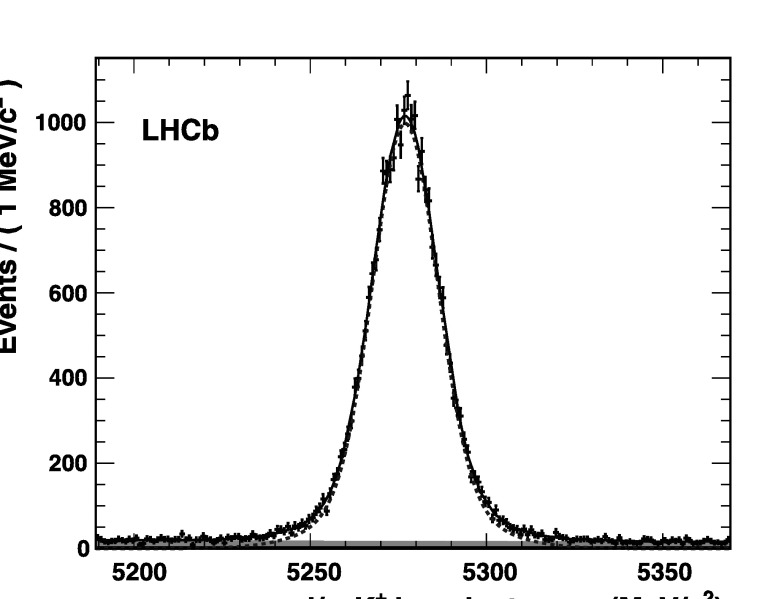
The parameters ω and εtag (defined in (2)) are different for signal and background. Figure 1 shows the mass distribution of the selected and tagged events, together with the superimposed fit.
Fig. 1.
Mass distribution of OS tagged B +→J/ψK + events. Black points are data, the solid blue line, red dotted line and green area are the overall fit, the signal and the background components, respectively (Color figure online)
Analysis of the B0→D∗−μ+νμ channel
The B0→D∗−μ+νμ channel is selected by requiring that a muon and the decay 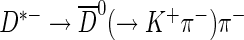 originate from a common vertex, displaced with respect to the pp interaction point. The muon and
originate from a common vertex, displaced with respect to the pp interaction point. The muon and 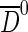 transverse momenta are required to be larger than 0.8 GeV/c and 1.8 GeV/c respectively. The selection criteria exploit the long B0 and
transverse momenta are required to be larger than 0.8 GeV/c and 1.8 GeV/c respectively. The selection criteria exploit the long B0 and 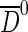 lifetimes by applying cuts on the impact parameters of the daughter tracks, on the pointing of the reconstructed B0 momentum to the primary vertex, on the difference between the z coordinate of the B0 and
lifetimes by applying cuts on the impact parameters of the daughter tracks, on the pointing of the reconstructed B0 momentum to the primary vertex, on the difference between the z coordinate of the B0 and 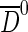 vertices, and on the
vertices, and on the 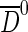 flight distance. Additional cuts are applied on the muon and kaon particle identification and on the quality of the fits of all tracks and vertices. In case of multiple B candidates per event the one with the smallest impact parameter significance with respect to the primary vertex is considered. Only events triggered in the HLT by a single particle with large momentum, large transverse momentum and large IP are used. In total, the sample consists of ∼482 000 signal events.
flight distance. Additional cuts are applied on the muon and kaon particle identification and on the quality of the fits of all tracks and vertices. In case of multiple B candidates per event the one with the smallest impact parameter significance with respect to the primary vertex is considered. Only events triggered in the HLT by a single particle with large momentum, large transverse momentum and large IP are used. In total, the sample consists of ∼482 000 signal events.
Even though the final state is only partially reconstructed due to the missing neutrino, the contamination of background is small and the background to signal ratio B/S is measured to be ∼0.14 in the signal mass region. The main sources of background are events containing a 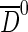 originating from a b-hadron decay (referred to as
originating from a b-hadron decay (referred to as 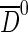 -from-B), events with a D∗− not from a b-hadron decay, decays of B+ mesons to the same particles as the signal together with an additional pion (referred to as B+) and combinatorial background. The different background sources can be disentangled from the signal by exploiting the different distributions of the observables m=mKπ, Δm=mKππ−mKπ, the reconstructed B0 decay time t and the mixing state q. The mixing state is determined by comparing the flavour of the reconstructed signal B0 at decay time with the flavour indicated by the tagging decision (flavour at production time). For unmixed (mixed) events q=+1(−1) while for untagged events q=0. The decay time is calculated using the measured B0 decay length, the reconstructed B0 momentum and a correction for the missing neutrino determined from simulation. It is parametrized as a function of the reconstructed B0 invariant mass.
-from-B), events with a D∗− not from a b-hadron decay, decays of B+ mesons to the same particles as the signal together with an additional pion (referred to as B+) and combinatorial background. The different background sources can be disentangled from the signal by exploiting the different distributions of the observables m=mKπ, Δm=mKππ−mKπ, the reconstructed B0 decay time t and the mixing state q. The mixing state is determined by comparing the flavour of the reconstructed signal B0 at decay time with the flavour indicated by the tagging decision (flavour at production time). For unmixed (mixed) events q=+1(−1) while for untagged events q=0. The decay time is calculated using the measured B0 decay length, the reconstructed B0 momentum and a correction for the missing neutrino determined from simulation. It is parametrized as a function of the reconstructed B0 invariant mass.
An extended unbinned maximum likelihood fit is performed by defining a PDF for the observables (m,Δm,t,q) as a product of one PDF for the masses and one for the t and q observables. For the 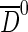 and D∗− mass peaks two double Gaussian distributions with common mean are used, while a parametric function motivated by available phase space is used to describe the Δm distributions of the
and D∗− mass peaks two double Gaussian distributions with common mean are used, while a parametric function motivated by available phase space is used to describe the Δm distributions of the 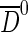 -from-B, and combinatorial background components. The decay time distribution of the signal consists of mixed, unmixed and untagged events, and is given by
-from-B, and combinatorial background components. The decay time distribution of the signal consists of mixed, unmixed and untagged events, and is given by
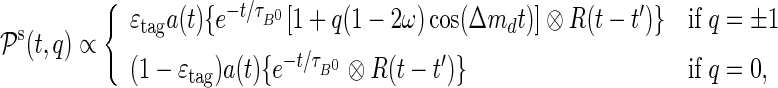 |
7 |
where Δmd and 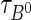 are the
are the 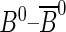 mixing frequency and B0 lifetime. The decay time acceptance function is denoted by a(t) and R(t−t′) is the resolution model, both extracted from simulation. A double Gaussian distribution with common mean is used for the decay time resolution model. In (7) the tagging parameters are assumed to be the same for B and
mixing frequency and B0 lifetime. The decay time acceptance function is denoted by a(t) and R(t−t′) is the resolution model, both extracted from simulation. A double Gaussian distribution with common mean is used for the decay time resolution model. In (7) the tagging parameters are assumed to be the same for B and 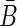 -mesons.
-mesons.
The decay time distributions for the B+ and 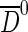 -from-B background components are taken as exponentials convolved by the resolution model and multiplied by the same acceptance function as used for the signal. For the prompt D∗ and combinatorial background, Landau distributions with independent parameters are used. The dependence on the mixing observable q is the same as for the signal. The tagging parameters εtag and ω of the signal and of each background component are varied independently in the fit, except for the B+ background where they are assumed to be equal to the parameters in the signal decay. Figure 2 shows the distributions of the mass and decay time observables used in the maximum likelihood fit. The raw asymmetry is defined as
-from-B background components are taken as exponentials convolved by the resolution model and multiplied by the same acceptance function as used for the signal. For the prompt D∗ and combinatorial background, Landau distributions with independent parameters are used. The dependence on the mixing observable q is the same as for the signal. The tagging parameters εtag and ω of the signal and of each background component are varied independently in the fit, except for the B+ background where they are assumed to be equal to the parameters in the signal decay. Figure 2 shows the distributions of the mass and decay time observables used in the maximum likelihood fit. The raw asymmetry is defined as
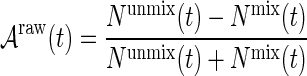 |
8 |
where Nmix (Nunmix) is the number of tagged events which have (not) oscillated at decay time t. From (7) it follows that the asymmetry for signal is given by
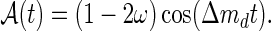 |
9 |
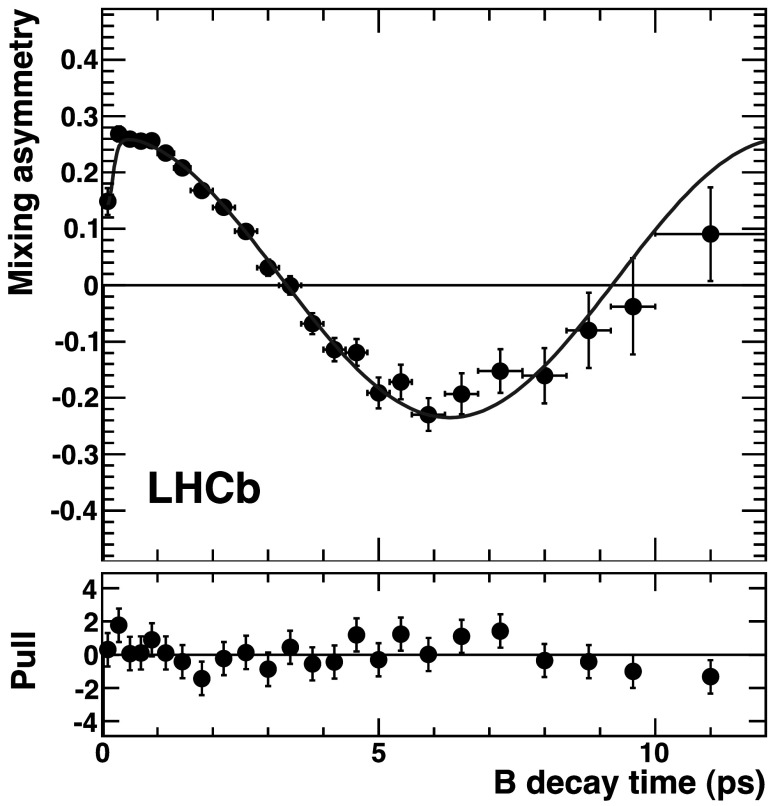
Figure 3 shows the raw asymmetry for the subset of events in the signal mass region that are tagged with the OS tagger combination. At small decay times the asymmetry decreases due to the contribution of background events, 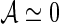 . The value of Δmd was fixed to Δmd=0.507 ps−1 [7]. Letting the Δmd parameter vary in the fit gives consistent results.
. The value of Δmd was fixed to Δmd=0.507 ps−1 [7]. Letting the Δmd parameter vary in the fit gives consistent results.
Fig. 2.
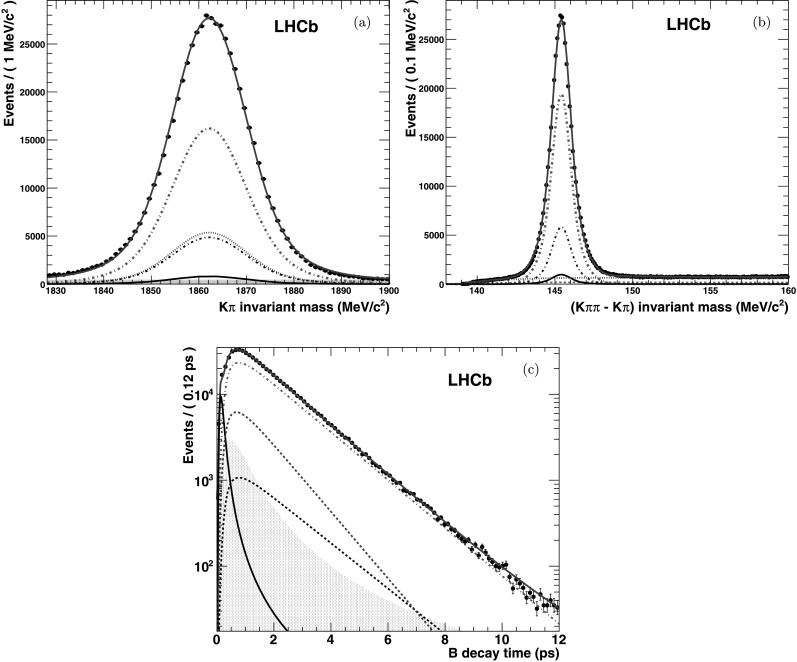
Distributions of (a) K
+
π
− invariant mass, (b) mass difference m(Kππ)−m(Kπ) and (c) decay time of the B
0→D
∗−
μ
+
ν
μ events. Black points with errors are data, the blue curve is the fit result. The other lines represent signal (red dot-dashed), 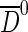 -from-B decay background (gray dashed), B
+ background (green short dashed), D
∗ prompt background (magenta solid). The combinatorial background is the magenta filled area (Color figure online)
-from-B decay background (gray dashed), B
+ background (green short dashed), D
∗ prompt background (magenta solid). The combinatorial background is the magenta filled area (Color figure online)
Fig. 3.
Raw mixing asymmetry of B 0→D ∗− μ + ν μ events in the signal mass region when using the combination of all OS taggers. Black points are data and the red solid line is the result of the fit. The lower plot shows the pulls of the residuals with respect to the fit (Color figure online)
Analysis of the B0→J/ψK∗0 channel
The B0→J/ψK∗0 channel is used to extract the mistag rate through a fit of the flavour oscillation of the B0 mesons as a function of the decay time. The flavour of the B0 meson at production time is determined from the tagging algorithms, while the flavour at the decay time is determined from the K∗0 flavour, which is in turn defined by the kaon charge.
The B0→J/ψK∗0 candidates are selected from J/ψ→μ+μ− and K∗0→K+π− decays. The J/ψ mesons are selected by the same selection as used for the B+→J/ψK+ channel, described in Sect. 4.1. The K∗0 candidates are reconstructed from two good quality charged tracks identified as K+ and π−. The reconstructed K∗0 meson is required to have a transverse momentum higher than 1 GeV/c, a good quality vertex and an invariant mass within ±70 MeV/c2 of the nominal K∗0 mass. Combinations of J/ψ and K∗0 candidates are accepted as B0 candidates if they form a common vertex with good quality and an invariant mass in the range 5100–5450 MeV/c2. The B0 transverse momentum is required to be higher than 2 GeV/c. The decay time and the invariant mass of the B0 are extracted from a vertex fit with an identical procedure as for the B+→J/ψK+ channel, by applying a constraint to the associated primary vertex, and a constraint to the J/ψ mass. In case of multiple B candidates per event, only the candidate with the smallest χ2 of the vertex is kept.
Only events that were triggered by the “lifetime unbiased” selection are kept. The B0 candidates are required to have a decay time higher than 0.3 ps to remove the large combinatorial background due to prompt J/ψ production. The sample contains ∼33 000 signal events.
The decay time distribution of signal events is parametrized as in (7), without the acceptance correction. The background contribution, with a background to signal ratio B/S∼0.29, is due to misreconstructed b-hadron decays, where a dependence on the decay time is expected (labeled “long-lived” background). We distinguish two long-lived components. The first corresponds to events where one or more of the four tracks originate from a long-lived particle decay, but where the flavour of the reconstructed K∗0 is not correlated with a true b-hadron. Its decay time distribution is therefore modeled by a decreasing exponential. In the second long-lived background component, one of the tracks used to build the K∗0 originated from the primary vertex, hence the correlation between the K∗0 and the B flavour is partially lost. Its decay time distribution is more “signal-like”, i.e. it is a decreasing exponential with an oscillation term, but with different mistag fraction and lifetime, left as free parameters in the fit.
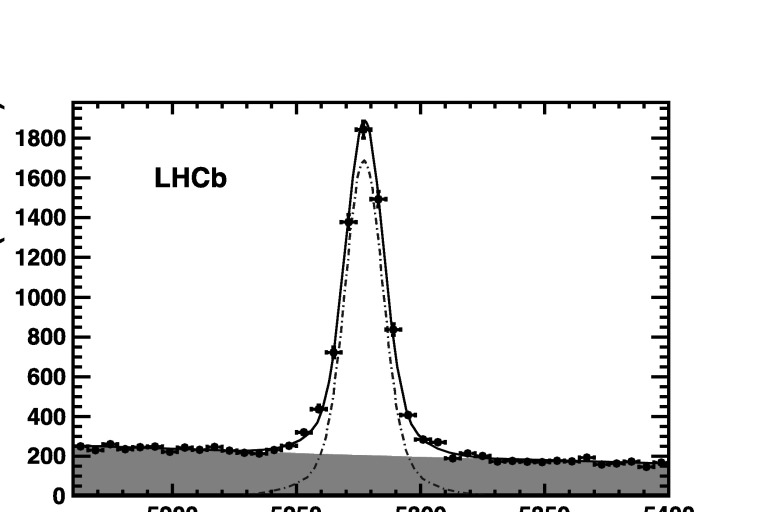
The signal and background decay time distributions are convolved with the same resolution function, extracted from data. The mass distributions, shown in Fig. 4, are described by a double Gaussian distribution peaking at the B0 mass for the signal component, and by an exponential with the same exponent for both long-lived backgrounds.
Fig. 4.
Mass distribution of OS tagged B 0→J/ψK ∗0 events. Black points are data, the solid blue line, red dotted line and green area are the overall fit, the signal and the background components, respectively (Color figure online)
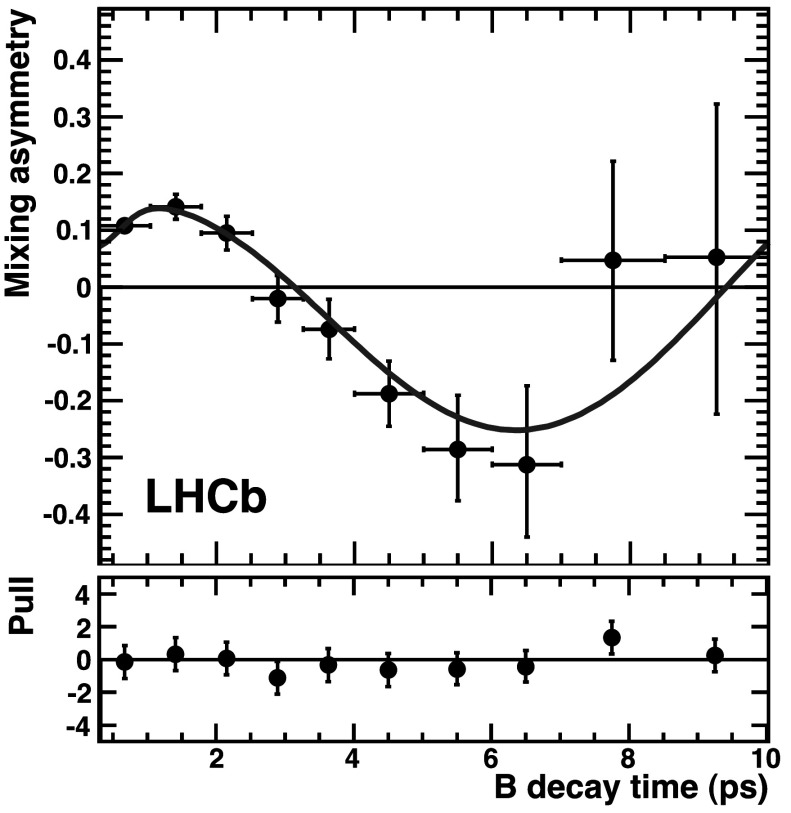
The OS mistag fraction is extracted from a fit to all tagged data, with the values for the B0 lifetime and Δmd fixed to the world average [7]. Figure 5 shows the time-dependent mixing asymmetry in the signal mass region, obtained using the information of the OS tag decision. Letting the Δmd parameter vary in the fit gives consistent results.
Fig. 5.
Raw mixing asymmetry of the B 0→J/ψK ∗0 events in the signal mass region, for all OS tagged events. Black points are data and the red solid line is the result of the fit. The lower plot shows the pulls of the residuals with respect to the fit (Color figure online)
Calibration of the mistag probability on data
For each individual tagger and for the combination of taggers, the calculated mistag probability (η) is obtained on an event-by-event basis from the neural network output. The values are calibrated in a fit using the measured mistag fraction (ω) from the self-tagged control channel B+→J/ψK+. A linear dependence between the measured and the calculated mistag probability for signal events is used, as suggested by the data distribution,
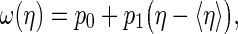 |
10 |
where p0 and p1 are parameters of the fit and 〈η〉 is the mean calculated mistag probability. This parametrization is chosen to minimize the correlation between the two parameters. Deviations from p0=〈η〉 and p1=1 would indicate that the calculated mistag probability should be corrected.
In order to extract the p0 and p1 calibration parameters, an unbinned maximum likelihood fit to the mass, tagging decision and mistag probability η observable is performed. The fit parametrization takes into account the probability density function of η, 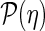 , that is extracted from data for signal and background separately, using events in different mass regions. For example, the PDF for signal events from (6) then becomes
, that is extracted from data for signal and background separately, using events in different mass regions. For example, the PDF for signal events from (6) then becomes
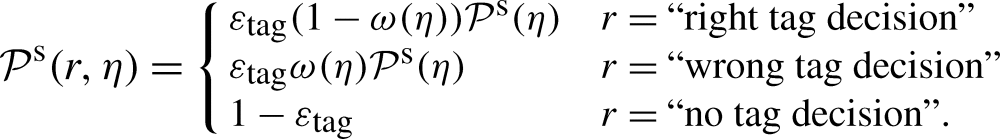 |
11 |
The measured mistag fraction of the background is assumed to be independent from the calculated mistag probability, as confirmed by the distribution of background events.
The calibration is performed on part of the data sample in a two-step procedure. Each tagger is first calibrated individually. The results show that, for each single tagger, only a minor adjustment of p0 with respect to the starting calibration of the neural network, performed on simulated events, is required. In particular, the largest correction is p0−〈η〉=0.033±0.005 in the case of the vertex charge tagger, while the deviations from unity of the p1 parameter are about 10 %, similar to the size of the corresponding statistical errors. In a second step the calibrated mistag probabilities are combined and finally the combined mistag probability is calibrated. This last step is necessary to correct for the small underestimation (p0−〈η〉=0.022±0.003) of the combined mistag probability due to the correlation among taggers neglected in the combination procedure. The calibrated mistag is referred to as ηc in the following.
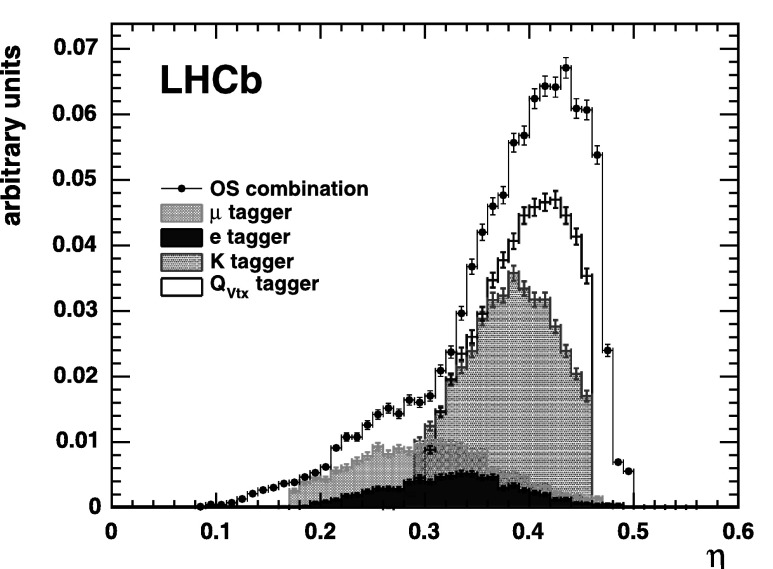
Figure 6 shows the distribution of the mistag probability for each tagger and for their combination, as obtained for B+→J/ψK+ events selected in a ±24 MeV/c2 mass window around the B+ mass.
Fig. 6.
Distribution of the calibrated mistag probability for the single OS taggers and their combination for B +→J/ψK + events selected in a ±24 MeV/c 2 mass window around the B + mass
Tagging performance
The tagging performances of the single taggers and of the OS combination measured after the calibration of the mistag probability are shown in Tables 2, 3 and 4 for the B+→J/ψK+, B0→J/ψK∗0 and B0→D∗−μ+νμ channels, respectively.
Table 2.
Tagging performance in the B +→J/ψK + channel. Uncertainties are statistical only
| Taggers | ε tag [%] | ω [%] | ε tag(1−2ω)2 [%] |
|---|---|---|---|
| μ | 4.8±0.1 | 29.9±0.7 | 0.77±0.07 |
| e | 2.2±0.1 | 33.2±1.1 | 0.25±0.04 |
| K | 11.6±0.1 | 38.3±0.5 | 0.63±0.06 |
| Q vtx | 15.1±0.1 | 40.0±0.4 | 0.60±0.06 |
| OS average (η c<0.42) | 17.8±0.1 | 34.6±0.4 | 1.69±0.10 |
| OS sum of η c bins | 27.3±0.2 | 36.2±0.5 | 2.07±0.11 |
Table 3.
Tagging performance in the B 0→J/ψK ∗0 channel. Uncertainties are statistical only
| Taggers | ε tag [%] | ω [%] | ε tag(1−2ω)2 [%] |
|---|---|---|---|
| μ | 4.8±0.1 | 34.3±1.9 | 0.48±0.12 |
| e | 2.2±0.1 | 32.4±2.8 | 0.27±0.10 |
| K | 11.4±0.2 | 39.6±1.2 | 0.49±0.13 |
| Q vtx | 14.9±0.2 | 41.7±1.1 | 0.41±0.11 |
| OS average (η c<0.42) | 17.9±0.2 | 36.8±1.0 | 1.24±0.20 |
| OS sum of η c bins | 27.1±0.3 | 38.0±0.9 | 1.57±0.22 |
Table 4.
Tagging performance in the B 0→D ∗− μ + ν μ channel. Uncertainties are statistical only
| Taggers | ε tag [%] | ω [%] | ε tag(1−2ω)2 [%] |
|---|---|---|---|
| μ | 6.08±0.04 | 33.3±0.4 | 0.68±0.04 |
| e | 2.49±0.02 | 34.3±0.7 | 0.25±0.02 |
| K | 13.36±0.05 | 38.3±0.3 | 0.74±0.04 |
| Q vtx | 16.53±0.06 | 41.5±0.3 | 0.48±0.03 |
| OS average (η c<0.42) | 20.56±0.06 | 36.1±0.3 | 1.58±0.06 |
| OS sum of η c bins | 30.48±0.08 | 37.0±0.3 | 2.06±0.06 |
The performance of the OS combination is evaluated in different ways. First the average performance of the OS combination is calculated, giving the same weight to each event. In this case, the best tagging power is obtained by rejecting the events with a poor predicted mistag probability ηc (larger than 0.42), despite a lower εtag. Additionally, to better exploit the tagging information, the tagging performance is determined on independent samples obtained by binning the data in bins of ηc. The fits described in the previous sections are repeated for each sub-sample, after which the tagging performances are determined. As the samples are independent, the tagging efficiencies and the tagging powers are summed and subsequently the effective mistag is extracted. The total tagging power increases by about 30 % with respect to the average value, as shown in the last line of Tables 2–4.
The measured tagging performance is similar among the three channels. The differences between the B+→J/ψK+ and B0→J/ψK∗0 results are large in absolute values, but still compatible given the large statistical uncertainties of the B0→J/ψK∗0 results. There are two reasons for the difference in the tagging efficiency for the B0→D∗−μ+νμ and the B→J/ψX channels. Firstly, their selections lead to different B momentum spectra which through production correlations give different momentum spectra of the tagging B. Secondly, the fraction of events passing the hardware trigger due to high transverse momentum leptons or hadrons produced in the opposite B decay differs.
Systematic uncertainties
The systematic uncertainties on the calibration parameters p0 and p1 are studied by repeating the calibration procedure on B+→J/ψK+ events for different conditions. The difference is evaluated between the value of the fitted parameter and the reference value, and is reported in the first row of Table 5. Several checks are performed of which the most relevant are reported in Table 6 and are described below:
The data sample is split according to the run periods and to the magnet polarity, in order to check whether possible asymmetries of the detector efficiency, or of the alignment accuracy, or variations in the data-taking conditions introduce a difference in the tagging calibration.
The data sample is split according to the signal flavour, as determined by the reconstructed final state. In fact, the calibration of the mistag probability for different B flavours might be different due to the different particle/antiparticle interaction with matter or possible detector asymmetries. In this case a systematic uncertainty has to be considered, unless the difference is explicitly taken into account when fitting for CP asymmetries.
The distribution of the mistag probability in the fit model,
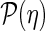 , is varied either by assuming the signal and background distributions to be equal or by swapping them. In this way possible uncertainties related to the fit model are considered.
, is varied either by assuming the signal and background distributions to be equal or by swapping them. In this way possible uncertainties related to the fit model are considered.
In addition, the stability of the calibration parameters is verified for different bins of transverse momentum of the signal B.
Table 5.
Fit values and correlations of the OS combined mistag calibration parameters measured in the B +→J/ψK +, B 0→J/ψK ∗0 and B 0→D ∗− μ + ν μ channels. The uncertainties are statistical only
| Channel | p 0 | p 1 | 〈η c〉 | p 0−p 1〈η c〉 | ρ(p 0,p 1) |
|---|---|---|---|---|---|
| B +→J/ψK + | 0.384±0.003 | 1.037±0.038 | 0.379 | −0.009±0.014 | 0.14 |
| B 0→J/ψK ∗0 | 0.399±0.008 | 1.016±0.102 | 0.378 | 0.015±0.039 | 0.05 |
| B 0→D ∗− μ + ν μ | 0.395±0.002 | 1.022±0.026 | 0.375 | 0.008±0.010 | 0.14 |
Table 6.
Systematic uncertainties on the calibration parameters p 0 and p 1 obtained with B +→J/ψK + events
| Systematic effect | δp 0 | δp 1 | δ(p 0−p 1〈η c〉) |
|---|---|---|---|
| Run period | ±0.005 | ±0.003 | ±0.004 |
| B-flavour | ±0.008 | ±0.067 | ±0.020 |
Fit model assumptions 
|
<±0.001 | ±0.005 | ±0.002 |
| Total | ±0.009 | ±0.07 | ±0.02 |
The largest systematic uncertainty in Table 6 originates from the dependence on the signal flavour. As a cross check this dependence is also measured with B0→D∗−μ+νμ events, repeating the calibration after splitting the sample according to the signal decay flavour. The differences in this case are δp0=±0.009 and δp1=±0.009, where the latter is smaller than in the B+→J/ψK+ channel. Both for the run period dependence and for the signal flavour the variations of δp0 and δp1 are not statistically significant. However, as a conservative estimate of the total systematic uncertainty on the calibration parameters, all the contributions in Table 6 are summed in quadrature.
The tagging efficiencies do not depend on the initial flavour of the signal B. In the case of the B+→J/ψK+ channel the values are (27.4±0.2) % for the B+ and (27.1±0.2) % for the B−.
Comparison of decay channels
The dependence of the calibration of the OS mistag probability on the decay channel is studied. The values of p0, p1 and 〈ηc〉 measured on the whole data sample for all the three channels separately, are shown in Table 5. The parameters p1 are compatible with 1, within the statistical uncertainty. The differences p0−p1〈ηc〉, shown in the fifth column, are compatible with zero, as expected. In the last column the correlation coefficients are shown.
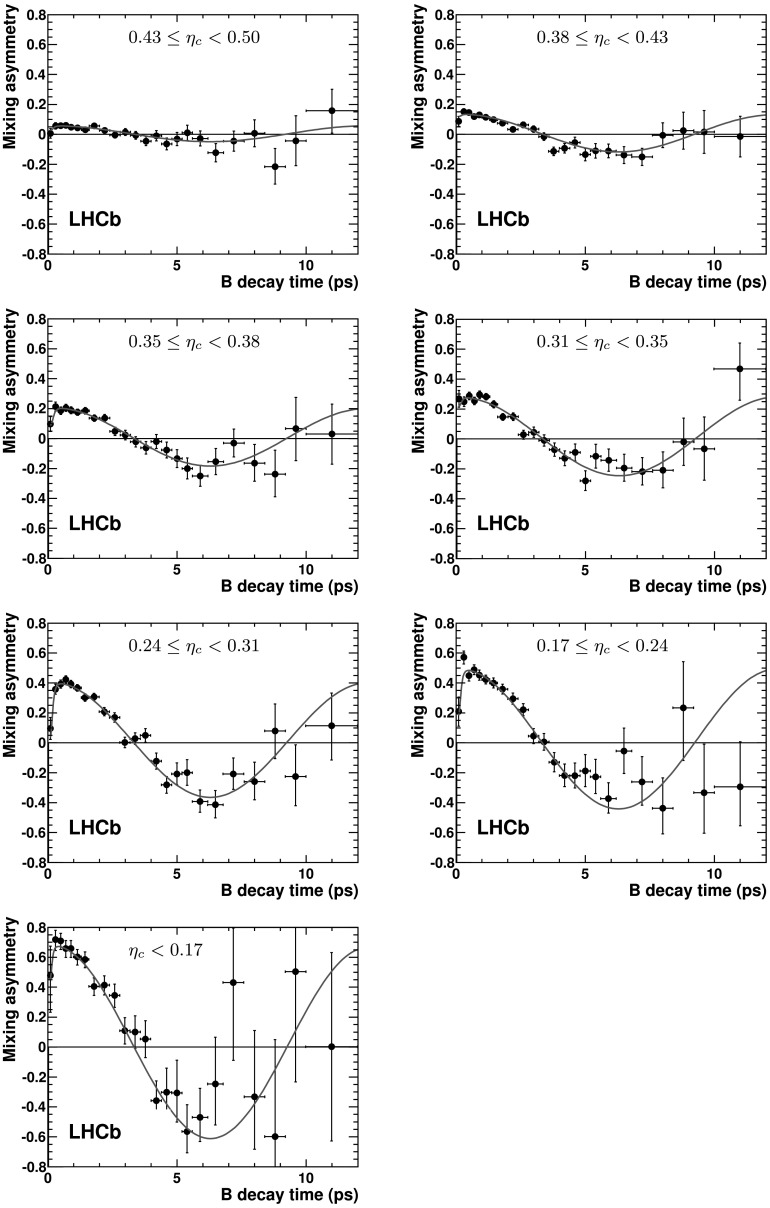
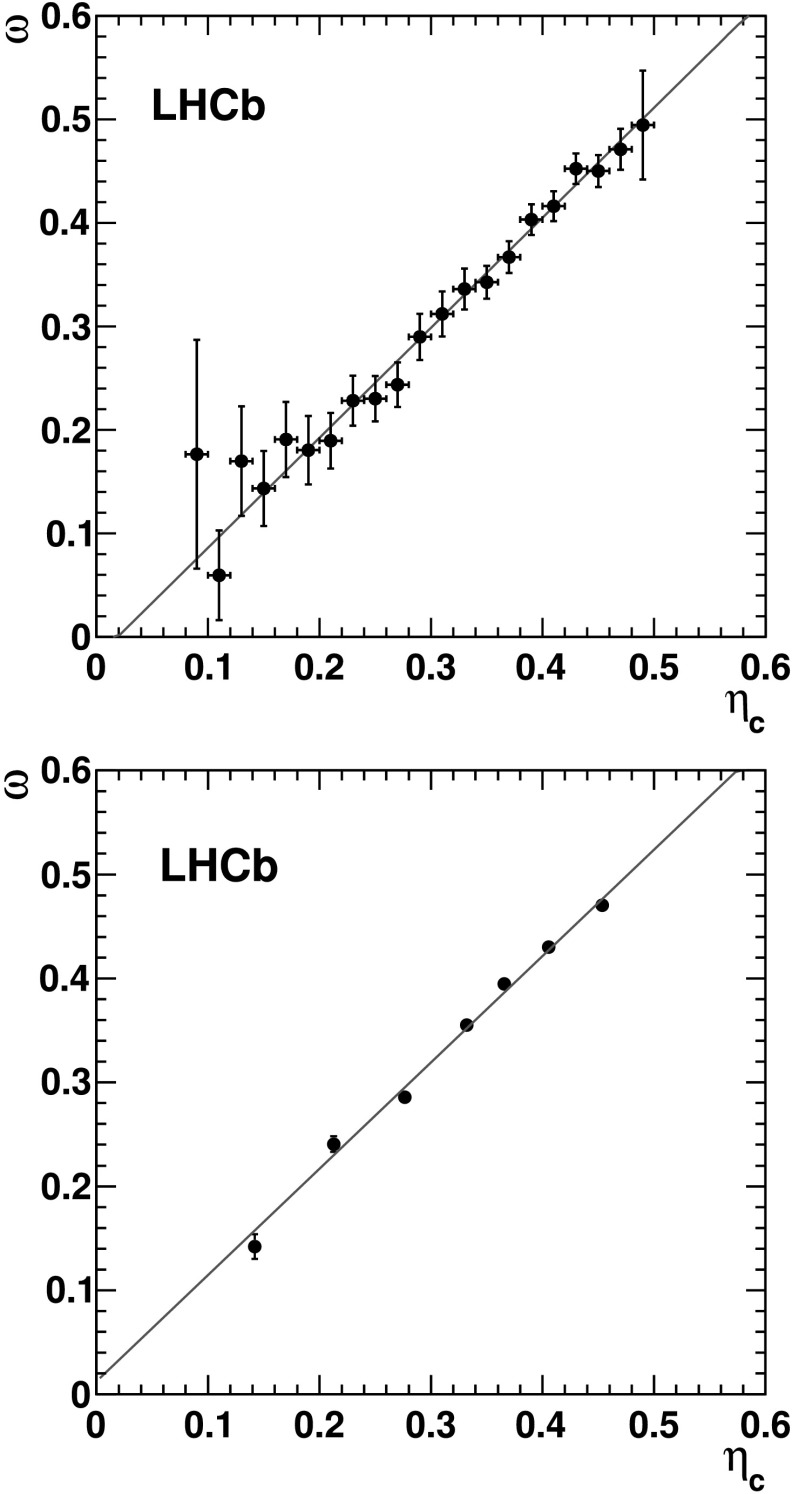
To extract the calibration parameters in the B0→J/ψK∗0 channel an unbinned maximum likelihood fit to mass, time and ηc is performed. In analogy to the B+→J/ψK+ channel, the fit uses the probability density functions of ηc, extracted from data for signal and background separately by using the sPlot [8] technique. The results confirm the calibration performed in the B+→J/ψK+ channel, albeit with large uncertainties. The results for the B0→D∗−μ+νμ channel are obtained from a fit to independent samples corresponding to different ranges of the calculated mistag probability as shown in Fig. 7. The trigger and offline selections, as well as signal spectra, differ for this decay channel with respect to the channels containing a J/ψ meson. Therefore the agreement in the resulting parameters is a validation of the calibration and its applicability to B decays with different topologies. In Fig. 8 the dependency of the measured OS mistag fraction as a function of the mistag probability is shown for the B+→J/ψK+ and B0→D∗−μ+νμ signal events. The superimposed linear fit corresponds to the parametrization of (10) and the parameters of Table 5.
Fig. 7.
Raw mixing asymmetry as a function of B decay time in B 0→D ∗− μ + ν μ events, in the signal mass region, using the OS tagger. Events are split into seven samples of decreasing mistag probability η c
Fig. 8.
Measured mistag fraction (ω) versus calculated mistag probability (η c) calibrated on B +→J/ψK + signal events for the OS tagger, in background subtracted events. Left and right plots correspond to B +→J/ψK + and B 0→D ∗− μ + ν μ signal events. Points with errors are data, the red lines represent the result of the mistag calibration, corresponding to the parameters of Table 5
The output of the calibrated flavour tagging algorithms will be used in a large variety of time-dependent asymmetry measurements, involving different B decay channels. Figure 9 shows the calculated mistag distributions in the B+→J/ψK+, B0→J/ψK∗0 and 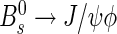 channels. These events are tagged, triggered by the “lifetime unbiased” lines and have an imposed cut of t>0.3 ps. The event selection for the decay
channels. These events are tagged, triggered by the “lifetime unbiased” lines and have an imposed cut of t>0.3 ps. The event selection for the decay 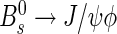 is described elsewhere [3]. The distributions of the calculated OS mistag fractions are similar among the channels and the average does not depend on the pT of the B. It has been also checked that the mistag probability does not depend on the signal B pseudorapidity.
is described elsewhere [3]. The distributions of the calculated OS mistag fractions are similar among the channels and the average does not depend on the pT of the B. It has been also checked that the mistag probability does not depend on the signal B pseudorapidity.
Fig. 9.
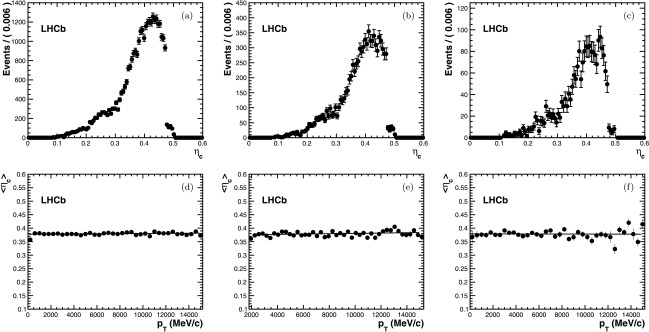
Top: calibrated mistag probability distribution for (a) B
+→J/ψK
+, (b) B
0→J/ψK
∗0 and (c) 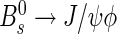 events. Bottom: distributions of the mean calibrated OS mistag probability as a function of signal p
T for the (d) B
+, (e) B
0 and (f)
events. Bottom: distributions of the mean calibrated OS mistag probability as a function of signal p
T for the (d) B
+, (e) B
0 and (f) 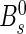 channels. The plots show signal events extracted with the sPlot technique and with the requirement t>0.3 ps. The three p
T distributions are fitted with straight lines and the slopes are compatible with zero
channels. The plots show signal events extracted with the sPlot technique and with the requirement t>0.3 ps. The three p
T distributions are fitted with straight lines and the slopes are compatible with zero
Event-by-event results
In order to fully exploit the tagging information in the CP asymmetry measurements, the event-by-event mistag probability is used to weight the events accordingly. The effective efficiency is calculated by summing the mistag probabilities on all signal events 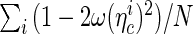 . We underline that the use of the per-event mistag probability allows the effective efficiency to be calculated on any set of selected events, also for non flavour-specific channels. Table 7 reports the event-by-event tagging power obtained using the calibration parameters determined with the B+→J/ψK+ events as reported in Table 5. The uncertainties are obtained by propagating the statistical and systematic uncertainties of the calibration parameters. In addition to the values for the three control channels the result obtained for
. We underline that the use of the per-event mistag probability allows the effective efficiency to be calculated on any set of selected events, also for non flavour-specific channels. Table 7 reports the event-by-event tagging power obtained using the calibration parameters determined with the B+→J/ψK+ events as reported in Table 5. The uncertainties are obtained by propagating the statistical and systematic uncertainties of the calibration parameters. In addition to the values for the three control channels the result obtained for 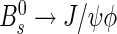 events is shown. For all channels the signal is extracted using the sPlot technique. The results for the tagging power are compatible among the channels containing a J/ψ meson. The higher value for B0→D∗−μ+νμ is related to the higher tagging efficiency.
events is shown. For all channels the signal is extracted using the sPlot technique. The results for the tagging power are compatible among the channels containing a J/ψ meson. The higher value for B0→D∗−μ+νμ is related to the higher tagging efficiency.
Table 7.
Tagging efficiency, mistag probability and tagging power calculated from event-by-event probabilities for B
+→J/ψK
+, B
0→J/ψK
∗0, B
0→D
∗−
μ
+
ν
μ and 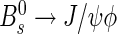 signal events. The quoted uncertainties are obtained propagating the statistical (first) and systematic (second) uncertainties on the calibration parameters determined from the B
+→J/ψK
+ events
signal events. The quoted uncertainties are obtained propagating the statistical (first) and systematic (second) uncertainties on the calibration parameters determined from the B
+→J/ψK
+ events
| Channel | ε tag [%] | ω [%] |
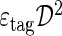 [%] [%] |
|---|---|---|---|
| B +→J/ψK + | 27.3±0.1 | 36.1±0.3±0.8 | 2.10±0.08±0.24 |
| B 0→J/ψK ∗0 | 27.3±0.3 | 36.2±0.3±0.8 | 2.09±0.09±0.24 |
| B 0→D ∗− μ + ν μ | 30.1±0.1 | 35.5±0.3±0.8 | 2.53±0.10±0.27 |
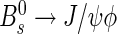
|
24.9±0.5 | 36.1±0.3±0.8 | 1.91±0.08±0.22 |
Summary
Flavour tagging algorithms were developed for the measurement of time-dependent asymmetries at the LHCb experiment. The opposite-side algorithms rely on the pair production of b and 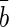 quarks and infer the flavour of the signal B meson from the identification of the flavour of the other b hadron. They use the charge of the lepton (μ, e) from semileptonic B decays, the charge of the kaon from the b→c→s decay chain or the charge of the inclusive secondary vertex reconstructed from b-hadron decay products. The decision of each tagger and the probability of the decision to be incorrect are combined into a single opposite side decision and mistag probability. The use of the event-by-event mistag probability fully exploits the tagging information and estimates the tagging power also in non flavour-specific decay channels.
quarks and infer the flavour of the signal B meson from the identification of the flavour of the other b hadron. They use the charge of the lepton (μ, e) from semileptonic B decays, the charge of the kaon from the b→c→s decay chain or the charge of the inclusive secondary vertex reconstructed from b-hadron decay products. The decision of each tagger and the probability of the decision to be incorrect are combined into a single opposite side decision and mistag probability. The use of the event-by-event mistag probability fully exploits the tagging information and estimates the tagging power also in non flavour-specific decay channels.
The performance of the flavour tagging algorithms were measured on data using three flavour-specific decay modes B+→J/ψK+, B0→J/ψK∗0 and B0→D∗−μ+νμ. The B+→J/ψK+ channel was used to optimize the tagging power and to calibrate the mistag probability. The calibration parameters measured in the three channels are compatible within two standard deviations.
By using the calibration parameters determined from B+→J/ψK+ events the OS tagging power was determined to be εtag(1−2ω)2=(2.10±0.08±0.24) % in the B+→J/ψK+ channel, (2.09±0.09±0.24) % in the B0→J/ψK∗0 channel and (2.53±0.10±0.27) % in the B0→D∗−μ+νμ channel, where the first uncertainty is statistical and the second is systematic. The evaluation of the systematic uncertainty is currently limited by the size of the available data sample.
Acknowledgements
We express our gratitude to our colleagues in the CERN accelerator departments for the excellent performance of the LHC. We thank the technical and administrative staff at CERN and at the LHCb institutes, and acknowledge support from the National Agencies: CAPES, CNPq, FAPERJ and FINEP (Brazil); CERN; NSFC (China); CNRS/IN2P3 (France); BMBF, DFG, HGF and MPG (Germany); SFI (Ireland); INFN (Italy); FOM and NWO (The Netherlands); SCSR (Poland); ANCS (Romania); MinES of Russia and Rosatom (Russia); MICINN, XuntaGal and GENCAT (Spain); SNSF and SER (Switzerland); NAS Ukraine (Ukraine); STFC (United Kingdom); NSF (USA). We also acknowledge the support received from the ERC under FP7 and the Region Auvergne.
Footnotes
Unless explicitly stated, charge conjugate modes are always included throughout this paper.
In the simulation the fraction of produced B0, B+, 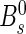 and baryon from the hadronization of the tagging B are the same as the inclusive fractions.
and baryon from the hadronization of the tagging B are the same as the inclusive fractions.
References
-
1.
R. Aaij et al. (LHCb collaboration), Measurement of the
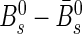 oscillation frequency Δms in
oscillation frequency Δms in 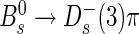 decays. arXiv:1112.4311. Submitted to Phys. Lett. B. doi:10.1016/j.physletb.2012.02.031
decays. arXiv:1112.4311. Submitted to Phys. Lett. B. doi:10.1016/j.physletb.2012.02.031
-
2.Aaij R., LHCb collaboration et al. Measurement of ϕs in
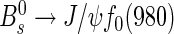 Phys. Lett. B. 2012;707:497. [Google Scholar]
Phys. Lett. B. 2012;707:497. [Google Scholar] -
3.
R. Aaij et al. (LHCb collaboration), Measurement of the CP violating phase ϕs in the decay
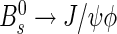 . arXiv:1112.3183. Submitted to Phys. Rev. Lett. doi:10.1103/PhysRevLett.108.101803
. arXiv:1112.3183. Submitted to Phys. Rev. Lett. doi:10.1103/PhysRevLett.108.101803
- 4.Abazov V.M., DØ collaboration et al. Measurement of Bd mixing using opposite-side flavor tagging. Phys. Rev. D. 2006;74 doi: 10.1103/PhysRevD.74.112002. [DOI] [Google Scholar]
- 5. T. Aaltonen et al. (CDF collaboration), Measurement of B0 oscillations and calibration of flavor tagging in semileptonic decays. http://www-cdf.fnal.gov/physics/new/bottom/060406.blessed-semi_B0mix/. CDF Note 8235
- 6.Alves A.A., Jr., LHCb collaboration et al. The LHCb detector at the LHC. J. Instrum. 2008;3 doi: 10.1088/1748-0221/3/08/S08005. [DOI] [Google Scholar]
- 7.Nakamura K., Particle Data Group et al. Review of particle physics. J. Phys. G. 2010;37 doi: 10.1088/0954-3899/37/7A/075021. [DOI] [Google Scholar]
- 8.Pivk M., Le Diberder F.R. sPlot: a statistical tool to unfold data distributions. Nucl. Instrum. Methods A. 2005;555:356. doi: 10.1016/j.nima.2005.08.106. [DOI] [Google Scholar]