On the problem of resonance assignments in solid state NMR of uniformly ¹⁵N,¹³C-labeled proteins

Abstract

Determination of accurate resonance assignments from multidimensional chemical shift correlation spectra is one of the major problems in biomolecular solid state NMR, particularly for relative large proteins with less-than-ideal NMR linewidths. This article investigates the difficulty of resonance assignment, using a computational Monte Carlo/simulated annealing (MCSA) algorithm to search for assignments from artificial three-dimensional spectra that are constructed from the reported isotropic ¹⁵N and ¹³C chemical shifts of two proteins whose structures have been determined by solution NMR methods. The results demonstrate how assignment simulations can provide new insights into factors that affect the assignment process, which can then help guide the design of experimental strategies. Specifically, simulations are performed for the catalytic domain of SrtC (147 residues, primarily β-sheet secondary structure) and the N-terminal domain of MLKL (166 residues, primarily α-helical secondary structure). Assuming unambiguous residue-type assignments and four ideal three-dimensional data sets (NCACX, NCOCX, CONCA, and CANCA), uncertainties in chemical shifts must be less than 0.4 ppm for all MCSA runs to yield fully correct assignments for SrtC, and less than 0.2 ppm for MLKL. Eliminating CANCA data has no significant effect, but additionally eliminating CONCA data leads to more stringent requirements for chemical shift precision. Introducing moderate ambiguities in residue-type assignments does not have a significant effect.

Introduction

Site-specific resonance assignments are usually a prerequisite for the extraction of useful structural or dynamical information from NMR spectra of proteins. When proteins are labeled with ¹⁵N and ¹³C only at specific sites or in a small number of amino acids [1, 2], assignments are trivial. However, when proteins are uniformly or extensively ¹⁵N,¹³C-labeled, as is now a standard practice in biomolecular solid state NMR, assignments must be obtained by an analysis of multiple multidimensional chemical shift correlation spectra [3–18]. Although in principle this analysis may seem straightforward, in practice it can be quite difficult, tedious, and error-prone. The limited signal-to-noise ratios and relatively broad lines of most solid state NMR spectra of proteins, compared with their solution NMR counterparts, makes the task of obtaining site-specific resonance assignments from multidimensional solid state NMR spectra especially problematic.

In an infamous paper published in 1996, when solid state NMR spectroscopy of uniformly labeled proteins under magic-angle spinning was in its infancy, I attempted to quantify how the difficulty of obtaining unique assignments would depend on the solid state NMR linewidths [19]. Using isotropic ¹⁵N and ¹³C chemical shifts from solution NMR studies of the 76-residue protein ubiquitin, I constructed a set of artificial three-dimensional (3D) spectra for protein segments of various lengths. I then used an elaborate computational algorithm to search for resonance assignments in a sequential manner, assuming various linewidths (i.e., various uncertainties in the precise values of the chemical shifts when comparing crosspeak positions from different 3D spectra). By running the same algorithm many times, I determined a lower limit on the number of distinct resonance assignments that were consistent with all 3D spectra, as a function of the assumed linewidth and the length of the protein segment. The main result was that the linewidths would have to be under 0.5 ppm for the assignments to be unique if the protein segment was more than 30 residues in length [19].

Although this old result is not terribly inaccurate, the 3D spectra considered in these old simulations were not the same as 3D spectra that are now used in real experiments on real proteins. Most importantly, sidechain chemical shifts were not included in the artificial 3D spectra. Moreover, the well-known correlations of ¹³C chemical shifts with residue type, which in practice are very important in the assignment process, were not used in the assignment algorithm.

More recently, as my research group began to study uniformly labeled proteins in noncrystalline states, such as amyloid fibrils and viral capsids [20–22], we realized that the “traditional” manual and sequential approach to resonance assignment, which can be very effective when applied to proteins with very sharp solid state NMR lines, can easily fail when applied to non-ideal (but scientifically interesting) systems. The main problem is that, although one may be able to find a plausible set of resonance assignments that seems fully consistent with one’s multidimensional spectra, there is no guarantee that this set of assignments is unique. We were therefore led to develop a more general computational approach for analyzing multidimensional data, based on a relatively simple and flexible Monte Carlo/simulated annealing (MCSA) algorithm [23, 24]. The MCSA algorithm allows us to treat nearly any combination of multidimensional spectra, to include partial residue-type assignments derived from chemical shift values (or from other information), and to repeat the assignment process many times in order to identify protein segments that have unique resonance assignments, segments that have non-unique assignments, and segments that are “invisible”. The same algorithm can also be applied to nucleic acids or other heteropolymers, and to solution NMR data. The MCSA algorithm, contained in a Fortran95 program called mcassign2b (available upon request from robertty@mail.nih.gov), has been used in several of our recent publications [20–22, 25].

The resonance assignment problem is a complicated one. The uniqueness of assignments from a given set of multidimensional data obviously depends on the linewidths and on the length of the protein sequence. It may also depend on the protein’s secondary structure, the diversity of the amino acid composition, the presence or absence of repetition in the sequence, and the extent of “invisible” segments (i.e., protein segments that do not contribute to the solid state NMR data, due to static or dynamic disorder). Since every protein has its own characteristics, both in terms of its biochemical/biophysical properties and its NMR properties, it is not possible to formulate definite rules that govern the uniqueness of assignments in all cases. Nonetheless, given the importance of the assignment problem, the time-consuming nature of sample preparations and solid state NMR measurements, the availability of the MCSA algorithm, and the relative ease of computer simulations, it makes sense to use computational simulations to investigate how the uniqueness of assignments depends on various factors. Results from assignment simulations can help guide one’s choice of samples and measurements in real experiments.

MCSA algorithm

Figure 1 shows a simplified flow chart for the MCSA algorithm [24]. One first prepares input files, including one file that contains the protein sequence, at least one signal table for each multidimensional spectrum that contains rows of correlated chemical shift values, linewidths (i.e., uncertainties in the chemical shifts), and residue-type assignments, and one file that specifies the “connections” between signal tables. Signal tables are created manually, by careful inspection of the experimental data to identify crosspeaks and sets of crosspeaks that correlate with one another. The number of chemical shift columns in each table can vary, but is normally at least equal to the dimension of the corresponding NMR spectrum. Residue-type assignments for each signal row need not be unambiguous, as discussed below. The connection table specifies which pairs of chemical shift columns from different signal tables should agree after signals (i.e., rows from signal tables) are assigned to specific residues.

Figure 1.

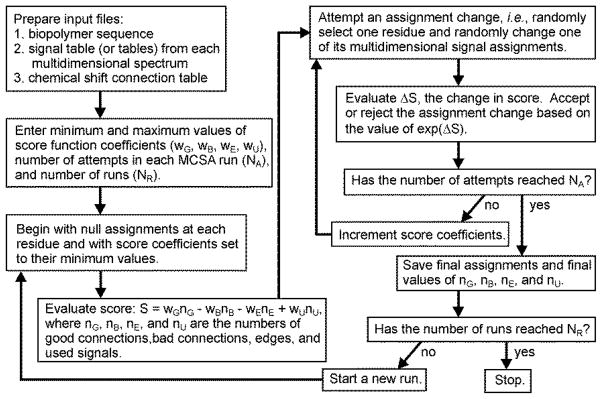
Flow chart for the Monte Carlo/simulated annealing algorithm for resonance assignment, as contained in the program mcassign2b.

One then runs the mcassign2b program, providing as input the minimum and maximum values of coefficients w_G, w_B, w_E, and w_U in the score function, the number of Monte Carlo attempts in each independent MCSA run, and the number of runs. The score for a given assignment of signals to residues in the protein sequence is defined to be S(n_G,n_B,n_E,n_U) = w_Gn_G − w_Bn_B − w_En_E + w_Un_U, where n_G is the number of good connections (i.e., agreements between chemical shifts from different signal tables), n_B is the number of bad connections (i.e., disagreements between chemical shifts from different signal tables), n_E is the number of assignment “edges” (i.e., connections that can not be tested due to gaps between the residues to which signals have been assigned), and n_U is the total number of rows from all signal tables that have been “used” (i.e., assigned to specific residues). In evaluating the connections, two chemical shifts are considered to agree when the square of their difference is less than the sum of their squared uncertainties.

The mcassign2b program seeks to maximize the score, which means maximizing the numbers of good connections and used signals and minimizing the numbers of bad connections and edges. Typically, the initial assignments at each residue are “null”, meaning that no signals are assigned to any residue. In each Monte Carlo attempt, the assignment from one randomly chosen signal table at one randomly chosen residue is changed (or replaced by a null assignment) and the concomitant change in score ΔS is evaluated. The attempt is then accepted or rejected according to the standard Metropolis condition [26]. That is, the attempt is accepted only if exp(ΔS) is greater than a random number between 0.0 and 1.0. As the run proceeds, the score function coefficients are increased from their minimum their maximum values, making the acceptance probability decrease toward zero.

Compared with the original mcassign2 program described by Hu et al. [24], our current mcassign2b program includes two additional features: (1) Rather than starting with null assignments, one can start with a set of tentative or partial assignments, determined from an earlier MCSA run or from other information; (2) Rather than increasing the score coefficients linearly from their minimum to their maximum values, the score coefficients can remain constant once the acceptance probability falls to a specified value, then increase to their maximum values toward the end of a run. These features were added to facilitate applications to larger proteins, as described by Bayro et al. [22]

It should be noted that many other research groups have developed and applied automated or computer-aided methods for obtaining resonance assignments from multidimensional NMR spectra [27–43], including methods that are conceptually related to the MCSA algorithm [35, 40]. The point of this article is not to demonstrate that a particular algorithm or program is the best choice for resonance assignments, but rather to illustrate how simulations can provide useful insights into various factors and requirements related to the uniqueness of assignments. Other algorithms or programs can certainly be used to accomplish the same ends.

Simulated assignments for two proteins with different secondary structures

Choice of proteins and construction of 3D spectra

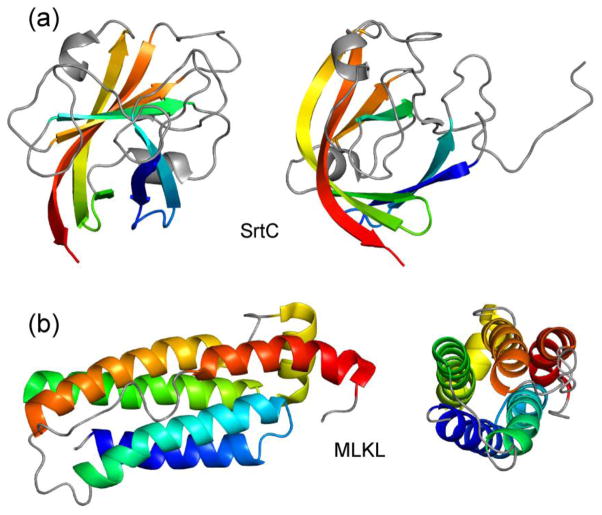
For the simulations described below, two proteins with similar sizes and with nearly complete ¹⁵N and ¹³C chemical shift assignments from solution NMR were chosen: (1) The 147-residue catalytic domain of the Bacillus anthracis sortase protein SrtC, whose structure was reported by Robson et al. [44] (Protein Data Bank code 2LN7, BioMagResBank code 18152); (2) The 166-residue N-terminal domain of the mixed-lineage kinase domain-like (MLKL) protein, whose structure was reported by Su et al. [45] (Protein Data Bank code 2MSV, BioMagResBank code 25135). As shown in Figure 2, these two proteins have quite different secondary structure compositions, with SrtC being primarily β-strands and MLKL being primarily α-helices.

Figure 2.

Cartoon representations of the structures of B. anthracis SrtC catalytic domain [44] (a) and MLKL N-terminal domain [45] (b), as determined by solution NMR (PDB 2LN7 and PDB 2MSV, respectively). Chemical shift values for these two proteins (BMRB 18152 and BMRB 25135) were used to generate artificial 3D solid state NMR spectra for assignment simulations. Each protein is viewed from two directions, approximately 90° apart. Signals from segments in grey were taken to be “invisible” in certain simulations, as discussed in the text.

For each protein, four signal tables representing artificial 3D solid state NMR spectra were constructed from the reported solution NMR chemical shifts. Rows in the first table, representing an NCACX spectrum, contain chemical shifts of N_i, CO_i, Cα_i, and Cβ_i, i.e., backbone amide nitrogen, backbone carbonyl carbon, α-carbon, and β-carbon of residue i. Rows in the second table, representing an NCOCX spectrum, contain chemical shifts of N_i+1, CO_i, Cα_i, and Cβ_i. Rows in the third table, representing a CONCA spectrum, contain chemical shifts of CO_i−1, N_i, and Cα_i. Rows in the fourth table, representing a CANCA spectrum, contain chemical shifts of Cα_i, N_i, and Cα_i−1. For SrtC, the NCACX, NCOCX, CONCA, and CANCA tables contained 119, 116, 110, and 116 signal rows, respectively. For MLKL, these tables contained 148, 148, 145, and 147 signal rows, respectively. The numbers of signal rows do not equal the numbers of residues in the protein sequences because certain chemical shift values are not available, especially for residues 1–6, 22, 38–41, 54, 65–74, 115, 122–124, 132, and 146 of SrtC and for residues 1–12, 52, 53, 65, 66, 93, 104, 106–108, 134, 135, 137, and 138 of MLKL.

Sidechain chemical shifts other than those of β-carbons are not included explicitly in the NCACX and NCOCX signal tables. In our experience, crosspeaks to sidechain carbons beyond β-carbons are often weak in experimental spectra, especially in the case of 3D NCOCX spectra, and do not contribute much information about connections between different 3D spectra. Sidechain chemical shifts beyond Cβ are more important for establishing residue-type assignments, which are included explicitly in the signal tables.

Chemical shift assignments from the BioMagResBank and signal tables for mcassign2b are contained in Supporting Information.

Dependence on chemical shift uncertainties

First, the dependence of MCSA results on the assumed uncertainties in chemical shift values was examined. Uncertainties of 0.1, 0.2, 0.3, 0.4, 0.6, and 0.8 ppm were tested. For each condition, 10 independent MCSA runs were performed, with 2 × 10⁸ attempts in each run. Score coefficients w_G, w_B, w_E, and w_U had minimum values of 0.0, 2.0, 0.0, and 0.0, and maximum values of 10.0, 50.0, 2.0, and 2.0. Each run was executed in approximately 200 s, using one core of an Intel Xeon E5640 processor. After each run, the final values of n_G, n_B, n_E, and n_U were stored and the final assignments of NCACX signals were compared with the correct NCACX assignments.

Results for SrtC and MLKL are summarized in Tables 1 and 2, which report the number of successful runs and the maximum number of incorrect assignments of NCACX signals (i.e., the largest number of NCACX signal rows that were assigned to the wrong residue) in the successful runs for each condition. Here, a successful run is defined as one for which the final value of n_B was zero and the final value of n_U equaled the total number of signal rows in all signal tables, i.e., a run that produced assignments that were fully consistent with information in the input files (but were not necessarily correct). Runs that produced assignments with bad connections or did not use all available signals were considered unsuccessful. Table 1 shows that, for SrtC, all successful runs with uncertainties of 0.3 ppm or less produced the correct assignments. However, larger uncertainties produced assignments that were fully consistent with the input files, but nonetheless were not entirely correct. Table 2 shows that, for MLKL, uncertainties above 0.1 ppm produced successful runs with incorrect assignments.

Table 1.

Summary of results from MCSA assignment simulations on SrtC catalytic domain (PDB 2LN7)

chemical shift uncertainties (ppm)	number of 3D spectra	ambiguous residue-type assignments?	“invisible” segments?	number of successful runs from 10 attempts	maximum number of incorrect NCACX assignments in successful runs
0.1	4	no	no	10	0
0.2	4	no	no	10	0
0.3	4	no	no	10	0
0.4	4	no	no	7	2
0.6	4	no	no	9	6
0.8	4	no	no	3	10
0.1	3	no	no	10	0
0.2	3	no	no	10	0
0.3	3	no	no	10	0
0.4	3	no	no	10	2
0.6	3	no	no	10	8
0.8	3	no	no	9	13
0.1	2	no	no	10	0
0.2	2	no	no	10	0
0.3	2	no	no	10	2
0.4	2	no	no	10	4
0.6	2	no	no	10	12
0.8	2	no	no	10	28
0.1	4	yes	no	10	0
0.2	4	yes	no	10	0
0.3	4	yes	no	8	0
0.4	4	yes	no	7	2
0.6	4	yes	no	6	6
0.8	4	yes	no	7	12
0.1	4	no	yes	10	0
0.2	4	no	yes	10	0
0.3	4	no	yes	10	0
0.4	4	no	yes	10	0
0.6	4	no	yes	10	2
0.8	4	no	yes	8	4

Table 2.

Summary of results from MCSA assignment simulations on MLKL N-terminal domain (PDB 2MSV)

chemical shift uncertainties (ppm)	number of 3D spectra	ambiguous residue-type assignments?	“invisible” segments?	number of successful runs from 10 attempts	maximum number of incorrect NCACX assignments in successful runs
0.1	4	no	no	10	0
0.2	4	no	no	10	4
0.3	4	no	no	5	6
0.4	4	no	no	2	8
0.6	4	no	no	0	-
0.8	4	no	no	0	-
0.1	3	no	no	10	0
0.2	3	no	no	10	4
0.3	3	no	no	10	12
0.4	3	no	no	10	14
0.6	3	no	no	5	26
0.8	3	no	no	2	48
0.1	2	no	no	10	4
0.2	2	no	no	10	8
0.3	2	no	no	9	22
0.4	2	no	no	10	26
0.6	2	no	no	0	-
0.8	2	no	no	1	87
0.1	4	yes	no	10	0
0.2	4	yes	no	10	4
0.3	4	yes	no	7	12
0.4	4	yes	no	1	8
0.6	4	yes	no	0	-
0.8	4	yes	no	0	-
0.1	4	no	yes	10	0
0.2	4	no	yes	10	4
0.3	4	no	yes	5	12
0.4	4	no	yes	3	8
0.6	4	no	yes	0	-
0.8	4	no	yes	0	-

These results highlight the complexity of the resonance assignment problem. Even with ideal data from four 3D spectra, including unambiguous residue-type assignments of all signals, it is possible to find assignments that include all available signals and are internally consistent, but still contain errors, unless the chemical shift uncertainties are quite small. Moreover, proteins with different sequences and secondary structures can present significantly different assignment difficulties.

Dependence on the number of 3D spectra

Next, the dependence of MCSA results on the number of available 3D spectra was examined, using either three (NCACX, NCOCX, CONCA) or two (NCACX, NCOCX) signal tables. As shown in Table 1, eliminating the CANCA data did not degrade the quality of the final NCACX assignments for SrtC, as no incorrect assignments from successful runs were observed with chemical shift uncertainties of 0.3 ppm or less. Additionally eliminating the CONCA data produced incorrect assignments with 0.3 ppm uncertainty. As shown in Table 2, eliminating the CANCA data also did not degrade the quality of final NCACX assignments for MLKL, but additionally eliminating the CONCA data led to incorrect assignments even with 0.1 ppm uncertainty in chemical shifts. These results suggest that information about sequential correlations of Cα chemical shifts may not be important in the assignment process, at least when unambiguous residue-type assignments are available, while sequential correlations of CO and Cα chemical shifts may be more valuable.

Effect of residue-type ambiguity

The assumption of entirely unambiguous residue-type assignments is rather unrealistic. Although certain residues, such as Ala, Ser, Thr, and Gly, can be reliably distinguished from others by their characteristic Cα and Cβ chemical shifts, most other residue types can not be identified unambiguously without observing at least several sidechain chemical shifts. Crosspeaks to sidechain sites beyond Cβ are often weak, absent, or difficult to identify in 3D spectra that are used for resonance assignments. Therefore, the effect of residue-type ambiguity on resonance assignments was examined next. Specifically, the NCACX signal tables were modified by replacing E and Q residue-type assignments with EQ residue-type assignments (meaning that Glu and Gln signals could be assigned to either Glu or Gln), H and W with HW, R and K with RK, D and N with DN, and F and Y with FY. Residue-type assignments in other signal tables were made more ambiguous, since sidechain signals are generally weaker in experimental NCOCX spectra and are absent from CONCA and CANCA spectra. Specifically, residue-type assignments were grouped as EQ, MKRHW, NDL, and FY in NCOCX signal tables and as NDLKMRHQEWFYC and VPI in CONCA and CANCA signal tables. Somewhat surprisingly, introduction of these residue-type ambiguities did not significantly affect the success rates of MCSA runs or the accuracy of NCACX assignments for either SrtC or MLKL, as shown in Tables 1 and 2. Greater ambiguities must eventually lead to inaccurate assignments, but this was not tested.

Effect of “invisible” segments

Finally, the effect of “invisible” segments was examined by eliminating signals from the grey-colored segments in Figure 2 from the signal tables. Essentially, signals from long stretches of irregular secondary structure, which might conceivably be attenuated by dynamic disorder in the solid state, were eliminated. Signals from β-strands in SrtC and α-helices in MLKL were retained, along with signals from relatively short loops. For SrtC, 65 NCACX signal rows, 63 NCOCX signal rows, 62 CONCA signal rows, and 64 CANCA signal rows were retained. For MLKL, the corresponding numbers were 124, 124, 123, and 124.

Although one might expect the introduction of “invisible” segments to impair the accuracy of the final resonance assignments (since bad connections could be avoided by creating additional gaps between segments with assigned signals), in fact the results in Tables 1 and 2 show no such effect for either SrtC or MLKL.

Discussion

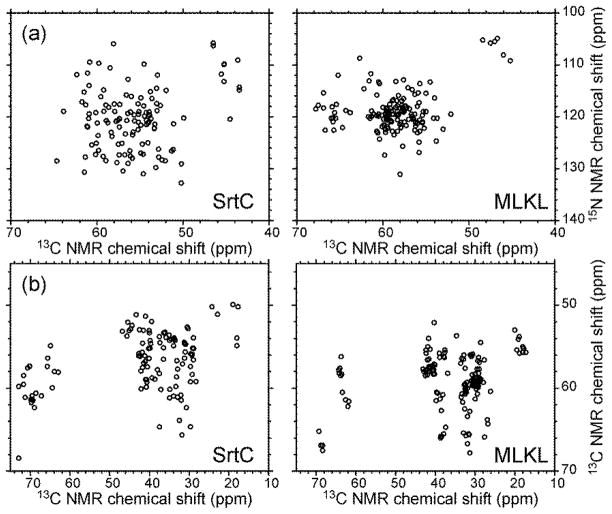
Several aspects of these resonance assignment simulations merit further discussion. First, it is clear that narrow NMR lines are a prerequisite for accurate assignments for proteins comprised of ~150 residues, even when high-quality 3D spectra can be obtained. Strictly speaking, the chemical shift uncertainties discussed above and indicated in Tables 1 and 2 are not the same as NMR linewidths, since the uncertainty can be significantly less than the linewidth if the signal-to-noise ratio is high. For example, a simple exercise in which noise is added to an ideal Gaussian lineshape and the result is fit with a Gaussian function indicates that the uncertainty in the peak position is less than one third of the full-width-at-half-maximum when the signal-to-noise (i.e., the ratio of the true peak height to the root-mean-squared noise) is 5:1. Interestingly, the requirement on chemical shift uncertainties is markedly different for the two proteins considered in these simulations, with smaller uncertainties being required in the case of MLKL. This difference is attributable to the lower degree of spectral dispersion for MLKL, as illustrated by the simulated 2D spectra in Figure 3, which is in turn attributable to the high αhelix content of the MLKL structure.

Figure 3.

Simulated 2D N-Cα (a) and Cα-Cβ (b) spectra of SrtC and MLKL.

Second, the simulations suggest that 3D CANCA spectra do not contain important assignment information that is complementary to the information in 3D NCACX, NCOCX, and CONCA spectra. This observation may have practical implications, since acquisition of a 3D CANCA spectrum can be time-consuming. Additional simulations on proteins with different sequences and secondary structures are required before the generality of this observation can be established. Simulations of this type, in which the numbers and properties of data sets are varied, can be a useful tool for designing efficient assignment strategies.

Third, although assignment simulations for SrtC and MLKL suggest that the presence of “invisible” segments does not increase the difficulty of determining unique resonance assignments, the situation may be different for other proteins. In particular, proteins with repetitive sequences are problematic, as it becomes difficult to assign signals uniquely to repeated sequence motifs if some of the repeats are “invisible” [20].

Fourth, complete assignment of all NMR signals is not necessarily a prerequisite for structural or dynamical studies. However, it is important to identify accurately the signals that do not have definite site-specific assignments. This identification can be made by comparing results of multiple MCSA runs.

Although only ¹⁵N and ¹³C chemical shifts are considered in the simulations described above, multidimensional solid state NMR spectra of proteins that include ¹H chemical shifts are also obtained in some experiments [46–48]. Simulations that include ¹H chemical shifts can be carried out with the mcassign2b program, without any modifications, and could be used to design assignment strategies for such experiments.

Finally, as shown in Tables 1 and 2, the number of successful MCSA runs decreased when the chemical shift uncertainties were large. Apparently, the “score landscape” (analogous to a potential energy landscape in protein folding simulations [49]) becomes rougher and the MCSA algorithm is more likely to become “trapped” in local score maxima. Similarly, a manual approach to sequential assignments is more likely to reach a “dead end” when the NMR linewidths are large. A larger number of attempts in each MCSA run generally increases the number of successful runs.

Highlights.

• Unique resonance assignments can be difficult to obtain

• The MCSA assignment algorithm can test for uniqueness

• Assignment simulations on artificial 3D data provide insights