Methods for Estimating Kidney Disease Stage Transition Probabilities Using Electronic Medical Records

Abstract

Chronic diseases are often described by stages of severity. Clinical decisions about what to do are influenced by the stage, whether a patient is progressing, and the rate of progression. For chronic kidney disease (CKD), relatively little is known about the transition rates between stages. To address this, we used electronic health records (EHR) data on a large primary care population, which should have the advantage of having both sufficient follow-up time and sample size to reliably estimate transition rates for CKD. However, EHR data have some features that threaten the validity of any analysis. In particular, the timing and frequency of laboratory values and clinical measurements are not determined a priori by research investigators, but rather, depend on many factors, including the current health of the patient. We developed an approach for estimating CKD stage transition rates using hidden Markov models (HMMs), when the level of information and observation time vary among individuals. To estimate the HMMs in a computationally manageable way, we used a “discretization” method to transform daily data into intervals of 30 days, 90 days, or 180 days. We assessed the accuracy and computation time of this method via simulation studies. We also used simulations to study the effect of informative observation times on the estimated transition rates. Our simulation results showed good performance of the method, even when missing data are non-ignorable. We applied the methods to EHR data from over 60,000 primary care patients who have chronic kidney disease (stage 2 and above). We estimated transition rates between six underlying disease states. The results were similar for men and women.

Introduction

The severity of many chronic diseases, including cancer and chronic kidney disease (CKD), are characterized, at least in part, by stages. The stage of disease and rate of progression or regression are important to deciding whether to treat, how to treat, and how often to monitor a patient. Moreover, knowledge about transition rates between stages helps patients understand what to expect and policymakers what to plan.

One approach for analyzing disease stage data is hidden Markov models (HMMs) (MacDonald and Zucchini 1997, 2009). Unlike ordinary Markov models, HMMs account for the fact that sometimes the observed disease stages are different from the underlying disease stages as a result of measurement error. Recently, researchers have used continuous-time HMMs to analyze data in a variety of clinical areas, such as hepatocellular cancer (Kay 1986), HIV progression (Satten and Longini 1996), and aortic aneurysms (Jackson 2003). However, a continuous-time model is computationally costly, and may be infeasible if the sample size is large, which is typically the case with electronic health records (EHR) data. Further, for many studies there would be no benefit to having finer information about the timing of a measurement than the calendar date. Discrete-time HMMs are a useful alternative, and have been developed and applied to a variety of health problems (Shirley et al. 2010; Rabiner 1986; Jackson and Sharples 2002; Scott 1999; Scott 2002; Scott et al. 2005; Gentleman et al. 1994; Bureau et al. 2000). While discrete-time HMMs have many desirable features, the estimation of transition rates typically requires large observational studies with long follow-up times as transitioning usually occurs over years. The resources required for such studies are often costly and time prohibitive. Use of longitudinal EHRs data from large primary care practices offers an alternative means of assembling longitudinal health experience of a population. Such data have the advantage of having both sufficient follow-up time and sample size to reliably and accurately estimate these rare transition rates.

In this paper we address challenges with using estimated glomerular filtration rate (eGFR) to study transition rates for chronic kidney disease (CKD). While large populations with years of longitudinal EHR data seem well suited for estimating CKD transition rates, two problems arise. First, unlike planned observational studies, digital patient records vary substantially in when (e.g., a patient seeks care for a problem) and why (i.e., a physician decides what to measure) a measurement is obtained, including measuring in relation to the severity of the underlying disease state. While eGFR is routinely measured on patients, the reason for measurement is also related to health status. Relatedly, measurement frequency varies substantially among patients and is often sporadic, leading to inferential challenges for handling these diverse types of missing data. Second, the size of the data set makes it challenging to fit complex models that involve computationally expensive optimization.

The objectives of this paper are to test methods for HMM that can address the challenges of estimating transition rates from large EHR data sets with irregular and potentially informative observation times. We deal with the size of the data and the irregularity of the observation times by developing a discretization method that transforms daily data (with a high degree of missingness) to data from wider time ranges. We use simulation studies to explore the impact of discretization assumptions on bias and variability, as well as on computing time.

In order to ensure that the simulation results are particularly relevant to CKD, we first conducted a preliminary analysis of the CKD data. In the simulation studies, we simulated data from models whose parameters were similar to those from the CKD analysis. To address concerns about potentially informative observation times (i.e., the decision to obtain or not obtain eGFR on a given date might depend on the observed health state), we conduct simulation studies where we apply our method to simulated data that have informative observation times. We find that the informative observation times do not have significant impact on the inference. We also demonstrate the feasibility of using this method on large EHR data, and present results from the CKD data as an illustration.

The rest of the paper is organized as follows: Section 2 describes the CKD study. Section 3 gives a brief introduction to HMMs and discusses in detail the HMM we proposed to fit the CKD data. Section 4 describes the simulation study and provides the results. The results of the CKD analysis are presented in Section 5. Finally, Section 6 includes a discussion of the findings, their implications, and some of the future research interests.

Background and Data

The study was approved by the Institutional Review Boards (IRBs) of Geisinger Health System and the University of Pennsylvania. Methods on CKD stages, access to EHR data, and HMM are described herein.

Chronic Kidney Disease

National Kidney Foundation Kidney Disease Outcome Quality Initiative (NKFKDOQI) classifies a patient’s CKD as being in one of five stages, defined by the level of the patient’s estimated glomerular filtration rate (eGFR) (Levy et al. 1999): kidney impairment with normal kidney function (stage 1, eGFR> 90), kidney impairment with mildly decreased kidney function (stage 2, eGFR 60-89), moderately decreased kidney function (stage 3, eGFR 44-59), severely decreased kidney function (stage 4, eGFR 15-29) and kidney failure (stage 5, eGFR< 15). Many patients who have CKD progress through these stages.

Data Description

All data for this study was derived from the Geisinger Health System (GHS), an integrated delivery system offering health care services to residents of 31 of Pennsylvania’s 67 counties with a significant presence in central and northeastern Pennsylvania. GHS includes the Geisinger Health Plan (GHP), an insurance plan, and the Geisinger Clinic (GC)—two major independent business entities with overlapping populations—as well as a host of other provider facilities (e.g., hospitals, addiction centers, etc.). GC primary care physicians manage approximately 400,000 patients annually. Adult (i.e., 18+ years of age) primary care patients were the source population for this study. These patients were similar to those in the region and were predominantly caucasian.

For this study, a database was created from EHR data of GC primary care patients that encompassed whether or not they were insured by GHP. All health information was integrated, including laboratory orders and results, medication orders, and inpatient (since 2007) and outpatient encounters. Longitudinal data were available for the period from July 30th, 2003 to Dec. 31st, 2009. Patients’ disease stages were evaluated according to eGFR values. Data were obtained from the National Kidney Registry and the Social Security Death Index, in order to determine dates at which any patients had dialysis, a kidney transplant, or died. Demographic variables routinely collected as part of patient care, such as age and gender, were also available.

Subjects were included in the study if they were between the ages of 30 and 75 years old, had Stage 2 or higher CKD at the time of their first eGFR, and had at least two valid values of disease stage (eGFRs, dialysis, kidney transplant, death). A total of 66,633 patients satisfied these criteria. Table 1 shows the baseline demographic information of our sample, where we define baseline as the date of first observed eGFR. The percentages of female and male were similar for patients who started with stage two CKD, but there were significantly more females than males who started with later stages of CKD. The mean age was 55 years old in both the male and female patients. The younger median age for stages 4 and 5 indicates the selection inherent to the prevalent sample because older patients are more common in more severe CKD stages and the risk of death among older patients is higher. There were 2,610 patients recorded with either dialysis, kidney transplant, or death as the outcome at the end of study.

Table 1.

Baseline demographic characteristics

	Female	Male	Total
Count
Stage 2–5 Stage 2 3 4 5	37,507(56%) 33,105(55%) 4,215(65%) 168(60%) 19(70%)	29,126(44%) 26,722(45%) 2,283(35%) 113(40%) 8(30%)	66,633 59,827 6,498 281 27
Median and IQR of age
All stages Stage 2 3 4 5	55(21) 54(20) 67(13) 64(14) 62(13)	55(20) 54(19) 66(13) 62(15) 61(12)	55(20) 54(20) 66(13) 63(15) 62(13)

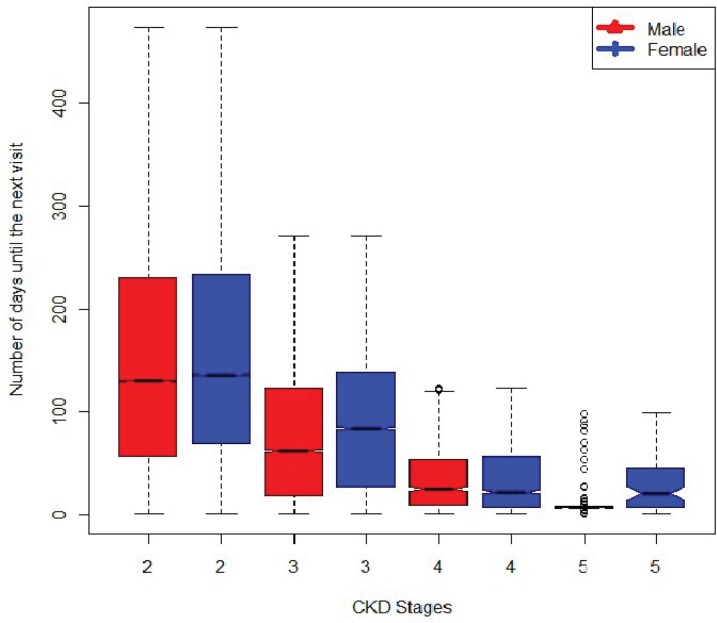
eGFR was obtained as part of a routine laboratory protocol and to monitor patients with CKD. As such, the time interval between lab measurements varied substantially among patients. The average number of eGFRs was four with a range of visits from 2 to 155 and a median number of 144 days between measurements with a range of 1 day to 2,169 days. Measurement of eGFR was more frequent for patients with more advanced stages of CKD increasing from a median of 144 days between measures for patients with Stage 2 CKD to 91 days for Stage 3 CKD patients, 22 days for Stage 4 CKD patients, and 11 days for stage 5 CKD patients. Figure 1 shows the distribution, by gender, of the number of days until the next visit for different CKD stages. Overall, the distributions are similar between men and women except for CKD stage 5 where men have more frequent visits than women. It should be noted that the data include both prevalent and incident cases.

Figure 1.

The boxplot shows the distributions, by CKD stages and gender, of the average number of days between measurements.

Statistical Model and Methodology

Introduction to Hidden Markov Model

A hidden Markov model (HMM) consists of two components: an observable component and an unobservable or “hidden” component. The hidden component behaves as a Markov process, which is a stochastic process with the memoryless property (MacDonald and Zucchini 2009). The property states that conditional on the present state of the process, its future and past are independent. Let h_t be the hidden state at time t, where t = 1, ...T, and assume each state can take a discrete value from the state space S, h_t = 1, ...S. For example, in the CKD example, h_t would represent the true (unobserved) disease state at time t, where the possible disease states are 1, 2, . . ., S. This “hidden” or ”latent” variable h, is assumed to follow the Markov process expressed below:

$$\text{Pr}\left(h_{t+1}=s|h_t=r,h_{t-1},...,h_1\right)=\text{Pr}\left(h_{t+1}=s|h_t=r\right)$$

where r, s ⊂ S. The above equation depicts a discrete-time HMM because the transition from State r at time t to State s at time t + 1 happens in an equally spaced time interval, denoted by a time increase of 1 unit. A time-homogeneous discrete-time HMM affirms the transition probability from state r to s is the same regardless of the time t:

$$\text{Pr}\left(h_{t+1}=s|h_t=r\right)=\text{Pr}\left(h_{t+k+1}=s|h_{t+k}=r\right)$$

Of course, because h is unobserved, estimation of transition rates will need to rely on linking observed variables to the unobserved variable. Let y_t denote the observed state at time t, t = 1, ...T, and take a discrete value from,1, ..., M. For example, in the CKD data y_t would represent the observed stage of CKD (1 to 5), based on eGFR. This may or may not coincide with the “true” disease state, as eGFR is measured with error and is an imperfect marker of disease. The probability of observing state m given that the hidden state is r at time t, is expressed as Pr(yt = m|ht = r). This is called the “state-dependent distribution” because the distribution of the observed value depends on the value of the hidden state.

There are three sets of parameters in a discrete-time HMM: the initial state probability, π, the transition probability matrix, Γ, and the state-dependent probability, P. The initial state probability, π = (π₁, ...π_S), specifies the distribution of the first hidden state, h₁. The transition probability matrix, Γ(S) where S denote the hidden state space, can be used to describe the distribution of the hidden state at time t + 1 given the hidden state at time t.

$$\Gamma (S)=\left(\begin{array}{cccc}{\gamma }_{11}& {\gamma }_{12}& \cdots & {\gamma }_{1S}\\ {\gamma }_{21}& {\gamma }_{22}& \cdots & {\gamma }_{2S}\\ ⋮& \ddots & \ddots & ⋮\\ {\gamma }_{S1}& {\gamma }_{S2}& \cdots & {\gamma }_{SS}\end{array}\right)$$

The element, γ12, for example, is the probability of transitioning from State 1 at time t to State 2 at time t + 1, Pr(γt+1 = 2|γt = 1). The transition probability matrix requires that each row must sum to 1: _jγ_ij = 1, i = 1, ...S. Given the hidden state at time t, the observed states are independent from each other and can take on a range of values with a probability distribution. It can be described using a probability matrix, P (S, M), where S denotes the hidden state space and M denotes the observed state space.

$$P\left(S,M\right)=\left(\begin{array}{cccc}{p}_{11}& p_{12}& \cdots & p_{1M}\\ p_{21}& p_{22}& \cdots & p_{2M}\\ ⋮& \ddots & \ddots & ⋮\\ p_{S1}& p_{S2}& \cdots & p_{SM}\end{array}\right)$$

The element, p12, for example, is the probability of observing State 2, given that the hidden state is 1 at time t, Pr(yt = 2|ht = 1). Like the transition probability matrix, each row of the state-dependent probability matrix must also sum to 1: M pij = 1, i = 1, ...S

The HMM for the CKD Data

If we assume that transitions between disease states are observed only at clinical visits, then a continuous-time HMM would be ideal to fit the CKD data because these visits happen at irregular times. However, such models require converting an instantaneous probability matrix to a probability matrix of time t in the construction of likelihood. It is computationally expensive because the probability matrix needs to be calculated at each time point for all the patients and the CKD data has many patients with long follow-up times. In our experience, built-in optimization functions in R, such as optim, have difficulty with likelihoods that involve latent classes and many parameters. Further, we attempted to use an existing R package for HMMs, but were unable to achieve convergence. If, however, we assume that transitions happen on a daily basis, then a discrete-time HMM can be used since transitions occur at a fixed interval length. A discrete-time HMM is more computationally efficient than a continuous-time HMM because it models a transition probability matrix rather than an instantaneous probability matrix. For daily transitions, ideally, we would like to observe the eGFR every day or on any given day. However, the observations of eGFR from EHRs are mostly sporadic. For purposes of modeling, we define all days between days with an observed eGFR to have a missing eGFR value. The combination of observed and missing values yields a very large data set that is computationally expensive to use for HMM. Moreover, the daily granularity of the data is far more refined than is necessary given the usual rate of change in eGFR. We therefore considered alternatives, where, rather than daily data, we explored the use of different interval lengths (30, 90, and 180 days). For example, when using a 30-day interval, we use the average of the multiple observed states within one interval to determine observed status. If this average is not an integer, then either the ceiling or the floor of the average will be used depending on the value of the last observed state in the interval. For example, if the average within a particular state is 2.4 and the last observed state is 4, State 3 will be the value in this interval. If the last observed state is 1, then State 2 will be used instead. In the last interval, if State 5 is observed along with other values, then State 5 will be used. If there are only missing values in the interval, then a missing value is assigned. We used simulation studies to explore the association between interval length and bias.

Once the CKD data are combined into different interval lengths, we use a discrete-time, time-homogeneous HMM with five observable states (1, 2, 3, 4, 5) to model the data. For the number of hidden states, we explored different possibilities, including 4, 5 and 6 state models. For this section, we will describe the model with five hidden states (A, B, C, D, E). Generalization to other number of states is straightforward. The first four observed states (State 1, 2, 3, 4) correspond to CKD stage 2, 3, 4, and 5, where State 5 is the absorbing state (kidney transplant, dialysis or death). Once a patient enters the absorbing state, the patient will stay in it permanently. In other words, if a patient has a kidney transplant, was put on dialysis, or died, the patient can no longer regress or progress naturally. Note that the hidden states do not necessarily correspond to the observed states (i.e., hidden state B does not have to imply observed state 2), except for the absorbing state. The meaning of the hidden disease states are based on the state dependent probabilities.

The HMM follows a natural disease progression model, in which transitions are only allowed to be between adjacent states and to the absorbing state (Jackson 2007). This model says, for example, that a transition from State B to State D does not happen unless a transition from State B to State C occurred first. Below is the assumed transition probability matrix for our model.

$$\Gamma (5)=\left(\begin{array}{ccccc}{\gamma }_{AA}& {\gamma }_{AB}& 0& 0& 1-{\gamma }_{AA}-{\gamma }_{AB}\\ {\gamma }_{BA}& {\gamma }_{BB}& {\gamma }_{BC}& 0& 1-{\gamma }_{BA}-{\gamma }_{BB}-{\gamma }_{BC}\\ 0& {\gamma }_{CB}& {\gamma }_{CC}& {\gamma }_{CD}& 1-{\gamma }_{CB}-{\gamma }_{CC}-{\gamma }_{CD}\\ 0& 0& {\gamma }_{DC}& {\gamma }_{DD}& 1-{\gamma }_{DC}-{\gamma }_{DD}\\ 0& 0& 0& 0& 1\end{array}\right)$$

We assume that, conditional on h_t ∈ {A, B, C, D}, h_t+1 has a multinomial distribution. The last row indicates that if the hidden state at time t is the absorbed state, then the probability of transitioning to other states at time t + 1 is 0.

The state dependent probability matrix accounts for measurement error in the observed data. Given the hidden state is j, the observed state expresses the error distribution, in this case, the distribution is multinomial.

We assume that only j or the adjacent states, j − 1 or j + 1, can the number of parameters needed to be estimated, and it seems to represent the majority of the measurement error in the CKD data. The absorbing state is assumed to be observed without error. This means that if a patient had a transplant or died, it would be recorded accurately without the possibility of error.

$$P\left(5,5\right)=\left(\begin{array}{ccccc}{p}_{A1}& 1-p_{A1}& 0& 0& 0\\ p_{B1}& p_{B2}& 1-p_{B1}-p_{B2}& 0& 0\\ 0& p_{C2}& p_{C3}& 1-p_{C2}-p_{C3}& 0\\ 0& 0& 1-p_{D4}& p_{D4}& 0\\ 0& 0& 0& 0& 1\end{array}\right)$$

Each row of the above matrix has a multinomial distribution with 0 probability of observing State 5 if the hidden state is not State E. The last row shows that if the hidden state is State E, then the probability of observing State 5 is 1.

Lastly, the initial hidden state probability distribution, which assigns probabilities to the hidden state at t = 1, will also have a multinomial distribution and can be represented with a vector, π=(π_A,...,π_D, 0). The last element of the vector is set to 0 because we assumed that patients cannot enter the study if they are already in State E.

Methodology

Assume the hidden state, h_it, where i = 1, ..., N and t = 1, ..., T_i, takes on a discrete value, s, from a sample space, S such that S = (A, B, C, D, E). The observed state, y_it, can also take on a discrete value, m, from a sample space, O, such that, m = 1, ..., M . At time t and given the hidden state, h_it, y_it can be observed from a state-dependent probability distribution. The likelihood of the observed data for all subjects given the parameter, θ = (π, Γ, P) is below:

$$\begin{array}{l}L\left(\theta |Y\right)=\prod _{i=1}^{N}L\left(\theta |Y_i\right)=\prod _{i=1}^N\sum _{h\in S^{T_i}}{\pi }_1\left(h_1\right)P_{h_1}\left(y_{i1}|\theta \right)\times \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\prod _{t=2}^{T_i}\gamma \left(h_{t-1},h_t\right)P_{h_t}\left(y_{\mathit{it}}|\theta \right)\end{array}$$

It is difficult to estimate θ directly from the above likelihood because of the product of summations. Instead, the expectation-maximization (EM) algorithm can be used; for HMMs, a special case of the EM algorithm was developed by Baum and Welch (1970) and is called the “Baum-Welch algorithm.” The EM algorithm makes use of the augmented likelihood of the complete data (observed data, Y, and hidden data, H):

$$\begin{array}{l}L\left(\theta |Y,H\right)\propto \prod _{i=1}^N\prod _{j=A}^E{\pi }_j^{I\left(h_{i1}=j\right)}\times \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\prod _{i=1}^N\prod _{t=2}^{T_i}\prod _{j=A}^E\prod _{k=A}^E{\gamma }_{jk}^{I\left(h_{\mathit{it}-1}=j\right)I\left(h_{\mathit{it}}=k\right)}\times \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\prod _{i=1}^N\prod _{t=1}^{T_i}\prod _{j=A}^E\prod _{k=1}^M{p}_{jk}^{I\left(h_{\mathit{it}}=j\right)I\left(y_{\mathit{it}}=k\right)}\end{array}$$

The EM algorithm involves iteratively computing the expected value of the observed likelihood given the current estimates of the parameters (the E-step) and then maximizing this observed likelihood over the parameters (the M-step). The computational details of the EM algorithm, the likelihood and θ are listed in the appendix. We use the nonparametric bootstrap to derive the standard errors (SEs). The resampling is done at the patient level.

Simulation Study

Data Generation

We conducted simulation studies to investigate the bias caused by different interval lengths and to investigate the effect of different missing data mechanisms on bias and variability. The reason for using intervals rather than analyzing daily data is to reduce the computational burden. The simulations are intended to provide information about the trade-off between bias, variability and computing time. As seen in Table 1, there is a large amount of variability in the frequency at which lab values are collected in EHRs. This is potentially a type of informative missing data. The simulation study is designed to provide insight into the effect that informative missingness might have on inference. Data in the simulation study were simulated to mimic the CKD data. We have used five hidden and five observed states to perform exploratory analysis on the CKD data. The results are used as the parameter values in the simulation. The simulation and all the analysis are coded in R.

First, complete daily status (i.e., no missing data) for 5,000 subjects, each with data up to six years, were generated using the discrete-time, time-homogeneous HMM described in section 3.2. The first hidden state, h_it, was generated with initial probabilities π = (0.80, 0.10, 0.07, 0.03, 0.0). Then, the first observed state, y_it, was generated with state-dependent probability matrix:

$$P\left(5,5\right)=\left(\begin{array}{ccccc}0.90& 0.10& 0& 0& 0\\ 0.10& 0.80& 0.10& 0& 0\\ 0& 0.10& 0.80& 0.10& 0\\ 0& 0& 0.10& 0.90& 0\\ 0& 0& 0& 0& 1\end{array}\right)$$

The rest of the data were created in two steps. In the first step, the hidden state at time t, h_it, t = 2, ..., T_i was generated using the transition probability matrix. The 180-day transition probability matrix is listed below.

$$\Gamma \left(5,5\right)=\left(\begin{array}{ccccc}0.90& 0.07& 0& 0& 0.03\\ 0.03& 0.85& 0.09& 0& 0.03\\ 0& 0.03& 0.80& 0.14& 0.03\\ 0& 0& 0.03& 0.75& 0.22\\ 0& 0& 0& 0& 1\end{array}\right)$$

The daily transition probability, which is used to generate the true disease status, can be derived by calculating Γ 180 . Since the progression of CKD at a later stage is more aggressive than that of an earlier stage, in the transition probability matrix, γ₄₅ > γ₃₄ > γ₂₃ > γ₁₂. We assumed that the regression of the disease was the same across all the states. In the second step, the observed state at time t, y_it, were generated with the state-dependent probability matrix again. This sequence of data were terminated when either six years of data were created or the absorbing state, State 5, was reached.

Missing Data Mechanisms

Next, we generated an indicator variable for missing data. Let W_it be the indicator variable of whether the value at time t was missing for subject i (equal to 1 if missing and 0 otherwise). We assumed that the first and the last values will always be observed. This assumption ensures that at least one transition will be observed for each subject.

We used three missing data mechanisms. The first missing data mechanism would be valid under the missing at random (MAR) assumption. MAR means that the missing data mechanisms depends only on the observed data. The missing data indicator variable, W_it, was generated sequentially, starting at visit 2 (since we assume no missing data at visit 1). In particular, we assume that Pr(W_it) depends only on the most recent observed value of y. For the second missing data mechanism, we assumed that Pr(W_it) depends only on y_{i,t − 1}, regardless of whether it was observed or not. This mechanism violates the MAR assumption because y_i,t−1 might not be observed, hence, it is a type of missing not at random (MNAR). We call this mechanism MNAR1.The final missing data mechanism that we considered assumes that the probability of missingness at time t depends only on the hidden state, h_it at time t. This mechanism also violates the MAR assumption because h is never observed. We call this mechanism “MNAR2.” The definitions for these three missing mechanisms are defined in Table 2.

Table 2.

Illustrations of different missing mechanisms

Missing Mechanism	Definition
MAR	Pr(Wit = 1|yij = 1)
MNAR1	Pr(Wit = 1|yit−1 = 1)
MNAR2	Pr(Wit = 1|hit = 1)

For each missing data mechanism, we further used three schemes to describe the differences in the number of days until the next visit. These three schemes are displayed in Table 3. Each cell gives the probability of being missing at each time. These probabilities determine how long on average a patient will wait until the next visit. The value in parentheses indicates the average number of days until the next visit. In scheme 1, the probability α_k is chosen so that the number of missing values between two observed values mimics the actual CKD data. In the CKD data, individuals with CKD stage 2 tend to have a longer time for the next eGFR measurement than individuals in CKD stage 3 and later stages. For patients in stage 2, the average time to the next measurement is 169 days. This time dropped down to 93 days for patients in stage 3, and so on. Hence, the lower the value of k, the higher the value of α_k. In scheme 2, α_k also depends on the value of k but the range for the number of days until the next visit (50–100 days) is shorter in length than the ones from scheme 1 (11–143 days). In scheme 3, the range of the duration (2–200 days) is longer in length than the ones from scheme 1 (11–143 days). α_k is assigned such that the sample size among the three schemes are similar. These schemes are intended to represent different realistic scenarios and are a good way to test the robustness of our model.

Table 3.

Probability of missing data on a given day, in each disease state, for each of the 3 missing data scenarios

Scheme	State 1	State 2	State 3	State 4
1	0.993 (143)	0.989 (91)	0.954 (22)	0.909 (11)
2	0.990 (100)	0.987 (77)	0.984 (62)	0.980 (50)
3	0.995 (200)	0.950 (20)	0.750 (4)	0.550 (2)

Note: The number in parentheses is the average number of days until the next observed value.

Finally, we used our “discretization” method to group the daily data into intervals of 30, 90, and 180 days.

Analysis

The convergence criteria used was less than 0.1 percent maximum difference between the current estimates and previous estimates. For each scenario and each parameter, we recorded the average value of the parameter estimates, the empirical standard deviation, and the absolute bias. In addition, the average time to convergence was recorded.

Results

We report detailed results here for all the missing data mechanisms in scheme 1 (the number of days till the next visit mimics the actual CKD data). The other two schemes had very similar results and are reported in the appendix. Table 4 lists the average computation time (seconds) used in 100 simulations for each interval length and the missing mechanisms. As expected, the convergence time decreases as the interval length increases. There seems to be more savings in going from the 30 day interval to the 90 day interval, compared to going from the 90 day to the 180 day interval. The computational times are not much different among different missing mechanisms within each interval length.

Table 4.

The average computation time (seconds)

Missing Mechanism	30 Day	90 Day	180 Day
MAR	9592	2821	2373
MNAR1	8602	4106	1513
MNAR2	9394	3790	2602

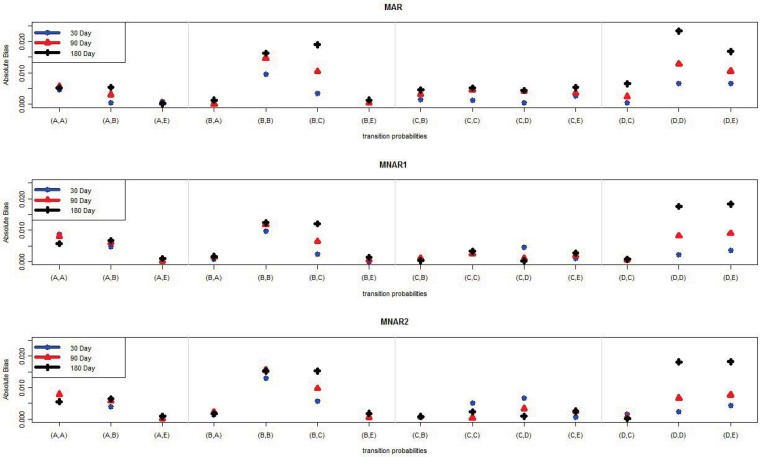
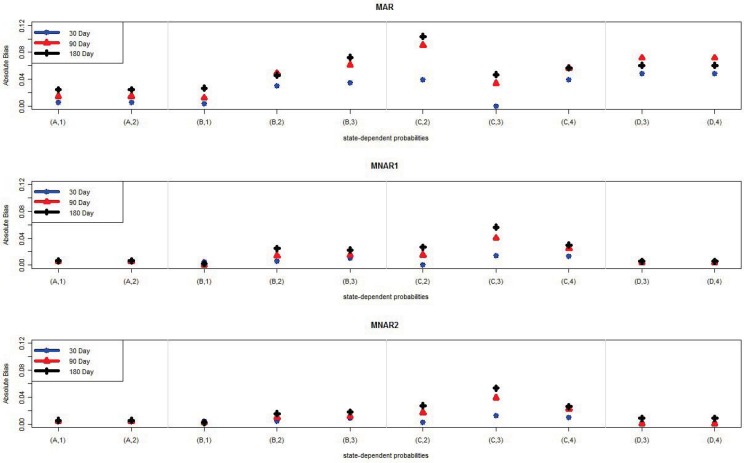
Tables 5–13 list the parameter estimates and empirical standard deviations (ESD) for the MAR, MNAR1, and MNAR2 mechanisms, respectively. Figures 2–3 show a graphical comparison of the absolute biases of different intervals and different missing mechanisms for the transition- and state-dependent probability parameters. The results show that, in general, there is not a lot of bias regardless of which interval length was selected. The estimates from the 30-day interval tended to have the least bias and the ones from the 180-day interval tended have the most bias. This result is not surprising since the shorter interval length means fewer data have been combined and more data are used for estimation. For example, consider the transition probability from State 4 to State 4, γ_DD. Under the MAR missing mechanism the absolute bias is 0.007 in the 30-day interval, 0.013 in the 90-day interval, and 0.023 in the 180-day interval. For each interval length, the absolute biases among the missing mechanisms are comparable. That is, we did not observe any pattern of biases tending to be larger for either NMAR1 or NMAR2, compared to MAR. We speculate in the Discussion section about why this might be the case.

Table 5.

Parameter estimates with MAR missing mechanism

	True value	θ̂(ESD)	θ̂(ESD)	θ̂ (ESD)
		30 Days	90 Days	180 Days
Initial Prob.
πA	0.80	0.799 (0.007)	0.794 (0.006)	0.775 (0.006)
πB	0.10	0.103 (0.005)	0.109 (0.005)	0.127 (0.006)
πC	0.07	0.069 (0.004)	0.068 (0.004)	0.068 (0.004)
πD	0.03	0.029 (0.002)	0.030 (0.002)	0.030 (0.002)

Table 13.

Parameter estimates with MNAR2 missing mechanism

	True value	θ̂(ESD)	θ̂(ESD)	θ̂(ESD)
		30 Days	90 Days	180 Days
State-dep. Prob.
pA1	0.90	0.904 (0.0016)	0.904 (0.0019)	0.905 (0.0026)
pA2	0.10	0.096 (0.0016)	0.096 (0.0019)	0.095 (0.0026)
pB1	0.10	0.104 (0.0024)	0.102 (0.0032)	0.102 (0.0041)
pB2	0.80	0.805 (0.0029)	0.810 (0.0043)	0.816 (0.0048)
pB3	0.10	0.091 (0.0022)	0.088 (0.0026)	0.082 (0.0036)
pC2	0.10	0.097 (0.0020)	0.083 (0.0034)	0.073 (0.0053)
pC3	0.80	0.812 (0.0026)	0.839 (0.0042)	0.853 (0.0058)
pC4	0.10	0.091 (0.0017)	0.078 (0.0032)	0.074 (0.0051)
pD3	0.10	0.101 (0.0025)	0.100 (0.0045)	0.091 (0.0072)
pD4	0.90	0.899 (0.0025)	0.900 (0.0045)	0.909 (0.0072)

Figure 2.

The absolute bias of the average of 14 transition probability parameter estimates of 100 samples for each interval length (30, 90, 180) under MAR, MNAR1, and MNAR2 missing mechanisms.

Note: (A,A) is the transition from State A to State A.

Figure 3.

The absolute bias of the average of 10 state-dependent probability parameter estimates of 100 samples for each interval length (30, 90, 180) under MAR, MNAR1, and MNAR2 missing mechanisms.

Note: (A,1) is observing state 1 giving the hidden state is State A.

For both the state-dependent and transition probability parameters, the ESD tended to increase as the interval length increased. This is expected since a widening interval decreases the number of data points. There was no difference in ESD for the initial probabilities, since the information for these parameters comes from the baseline data (not affected by interval length choice). We observed a larger impact of interval length on ESD than we did on bias. Thus, when choosing an interval length, the primary considerations should be the trade-off between standard errors and computational feasibility.

Application to CKD Data

We applied our proposed HMM, described in Section 3.2, to the CKD data, which were described in Section 2. We decided to use a 90-day time window, as that seemed to be a reasonable trade-off between computational feasibility and efficiency. We fitted separate models for men and women.

Number of Hidden States

Models with four, five, and six hidden states were fitted to the data for both male and female subgroups with an interval length of 90 days. We decided not to consider a seven state model because a model with several more latent states than observed states can become unstable. The Akaike information criterion (AIC) and the Bayesian information criterion (BIC) were calculated for all the models (four, five, six hidden states). The results are listed in Table 14. The HMM with six hidden states produced much smaller AIC (105222.1 for male, 154025.1 for female) and BIC (105424.7 for male, 154227.7 for female) values than the ones with four hidden states and five hidden states. Since the smaller AIC or BIC indicates a better fit of the model, we decided to fit the data with a six hidden state (A, B, C, D, E, F) and five observed state (1, 2, 3, 4, 5) model.

Table 14.

Comparison of HMMs

	Four hidden states	Five hidden states	Six hidden states
Men
AIC	108,895	106,224	105,222
BIC	109,009	106,378	105,424
Women
AIC	158,880	155,665	154,025
BIC	158,994	155,819	154,227

Parameter estimates and standard errors, stratified by sex, are displayed in Tables 15–17.

Table 15.

Parameter estimates for the CKD data: 90 Day

	Women	Men
	Estimate (SE)	Estimate (SE)
Initial Prob.
πA	0.799 (0.0080)	0.862 (0.0032)
πB	0.122 (0.0066)	0.081 (0.0033)
πC	0.074 (0.0025)	0.053 (0.0021)
πD	0.005 (0.0045)	0.004 (0.0004)
πE	0.000 (0.0001)	0.000 (0.0001)

Table 17.

Parameter estimates for the CKD data: 90 Day

	Women	Men
	Estimate (SE)	Estimate (SE)
State-dep. Prob.
pA1	0.980 (0.0010)	0.986 (0.0007)
pA2	0.020 (0.0010)	0.014 (0.0007)
pB1	0.583 (0.0194)	0.584 (0.0165)
pB2	0.416 (0.0193)	0.414 (0.0164)
pB3	0.001 (0.0003)	0.002 (0.0003)
pC1	0.025 (0.0026)	0.020 (0.0033)
pC2	0.964 (0.0021)	0.968 (0.0031)
pC3	0.011 (0.0013)	0.012 (0.0013)
pD2	0.143 (0.0177)	0.130 (0.0192)
pD3	0.847 (0.0172)	0.861 (0.0187)
pD4	0.010 (0.0019)	0.009 (0.0033)
pE3	0.174 (0.0565)	0.050 (0.0541)
pE4	0.826 (0.0565)	0.950 (0.0541)

State-Dependent Probabilities

We begin with the state-dependent probability results, because these provide information about the interpretation of the hidden states. Recall that we focused on CKD stages 2–5 (along with the absorbing state). Thus, observed state y = 1 corresponds to CKD stage 2. Observed state y = 5 is the absorbing state (transplant, dialysis, or death). Hidden state F always corresponds with observed state 5. From the results in men (women have similar results), we see that hidden state A almost always corresponds with observed state 1 (stage 2 CKD). However, hidden state B is a mixture of observed state 1 (probability 0.58) and observed state 2 (probability 0.41). Thus, we could think of hidden state B as subjects who might be near the CKD stage 2 and 3 boundary. Ninety-seven percent of the time, hidden state C corresponds with observed state 2. Thus, we could think of hidden state C as CKD stage 3. This finding suggests that it might be clinically meaningful to divide stage 3 into stage 3a and 3b where some patients progress to the next stage while others do not. With hidden state D, state 3 has been observed 86 percent of the time and observed state 4 only 9 percent of the time. Thus, we could think of hidden state D as being subjects who are typically in CKD stage 4. Finally, 95 percent of the time, hidden state E corresponds with observed state 4. Thus, we could think of hidden state E as subjects who are in CKD stage 5. The SEs are very small in general, but are particularly small for the parameters involving hidden states A to C. We estimate p_D3 and p_D4 with a little less accuracy, which is not surprising due to the fact that there are far fewer subjects in later disease stages.

Initial State Probabilities

Initially, about 86 percent of men and 80 percent of women were in hidden state A. Approximately 8 percent were in State B and 5 percent in State C for men and 12 percent were in State B and 7 percent in State C for women. Very few subjects began in hidden state D and almost none of them began in hidden state E. All of these parameter estimates had very small SEs (less than 0.005).

Transition Probabilities

The transition probabilities refer to the probabilities of transitioning from one hidden state to another within a 90-day period. In general, subjects are likely to remain in the same disease state over a 90-day period, with all of the same state probabilities at 0.70 and above. Subjects who were in State B were more likely to transition to State C than to State A. However, subjects who were in States C were more likely to transition to State B than to State D. Subjects who were in state D were equally likely to transition to state C and state E. In general, the results are very similar for men and women, with the exception being that the transition from State E to the absorbing State F is higher for men (0.26) than for women (0.16).

Progression probabilities (transition to the next higher state) has the following pattern: low for A to B, then increase for B to C, then decrease for C to D, but then increase for D to E and again for E to F. This pattern is consistent with what one might expect if there is a pathophysioligic channel at State C that determines if someone will have progressive disease.

Discussion

In this paper, we made novel use of a large EHR data set to estimate disease stage transition rates. Using EHR data for this purpose has many challenges, including the size of the data and the extreme variation (and likely informativeness) in the observation times. We proposed a discretization method to convert a continuous-time HMM to a discrete-time HMM and studied the effect of different amounts of discretization in a simulation study. We also investigated, via simulations, what effect disease stage-dependent observation times will have on the results. This is a common challenge with EHR data, where, typically: (1) more severe disease means more visits and a greater likelihood of being observed; and (2) the more one is observed the more the observations are conditioned by a desire to monitor.

The simulation results were promising for the method of discretization, in that the amount of bias was relatively small, even for the 180-day time window. Perhaps surprisingly, we found very little impact of nonignorable missing data on bias and variability. The missing data mechanisms that we considered depended on current or recent disease states. Other mechanisms might lead to more bias. Perhaps, for example, if the probability of missing data depended on the proximity to a transition, rather than the current disease state, there would be more bias. This is an area in need of further research.

For the CKD data, we found that of the four, five, and six hidden state models that we considered, the six hidden state model fits the data best. In the six state model, we found that all the CKD disease stages correspond to at least one hidden state in the model. One hidden state consists of subjects who are between stage 2 and 3. This suggests that there may be a disease state that is not well captured by the current five stage classification system. It also suggested that distinguishing CKD stage 3 into a stage 3a and stage 3b may be clinically sensible and correspond to empirical observations that some patients transition to a more severe stage while most patients do not. Within a 90-day period, transitions between hidden states were rare. The disease course, in terms of transitions between states, was very similar for men and women.

There were some limitations to this research. First, it should be noted that the population was mostly white and mostly from rural Pennsylvania (40 percent rural, whereas the national average is 20 percent), and might not be representative of the general population. Second, we used observed stages of CKD rather than eGFR values themselves. An alternative approach would be to relate eGFR values to hidden states. However, this approach is more computationally burdensome. Third, despite promising simulation results, we cannot rule out the possibility that selection bias (in terms of who had eGFR measured when) biased the results. It is also important to note that while a 90-day interval seemed to have good properties for CKD, a shorter window might be necessary for diseases that have rapid progression.

There is great potential for using EHR data to study characteristics of chronic diseases, due to the large population size and long follow-up times. The proposed discretization method makes the use of HMMs applied to large data sets more practical. While the simulation studies were promising, it will also be important to validate these results on a longitudinal CKD data set that was part of a research study (with planned data collection times and uniform standards). While transition rates themselves are important for understanding disease progression, the methods proposed here can be extended to another important area—prediction modeling. It is of interest to clinicians to be able to know who is likely to be a fast or slow progressor. Our models can be extended to allow transition rates to vary as a function of clinical predictors. The most direct way to do this is using stratification, like was done here for gender. For many predictors, the model could be extended to allow several latent classes for disease transition rates, with latent class probabilities depending on covariates. Relatedly, the model could be extended to have the disease transition rates vary from person to person according to a random effects distribution where the covariates may predict the random effects (Altman, 2007; Shirley et al., 2010)

Table 6.

Parameter estimates with MNAR1 missing mechanism

	True value	θ̂ (ESD)	θ̂ (ESD)	θ̂ (ESD)
		30 Days	90 Days	180 Days
Initial Prob.
πA	0.80	0.787 (0.006)	0.777 (0.007)	0.754 (0.007)
πB	0.10	0.109 (0.006)	0.121 (0.005)	0.143 (0.007)
πC	0.07	0.072 (0.003)	0.071 (0.003)	0.072 (0.003)
πD	0.03	0.031 (0.002)	0.031 (0.002)	0.032 (0.003)

Table 7.

Parameter estimates with MNAR2 missing mechanism

	True value	θ̂ (ESD)	θ̂(ESD)	θ̂(ESD)
		30 Days	90 Days	180 Days
Initial Prob.
πA	0.80	0.791 (0.006)	0.781 (0.006)	0.758 (0.006)
πB	0.10	0.105 (0.005)	0.116 (0.005)	0.138 (0.006)
πC	0.07	0.073 (0.004)	0.072 (0.004)	0.071 (0.004)
πD	0.03	0.031 (0.002)	0.031 (0.002)	0.033 (0.003)

Table 8.

Parameter estimates with MAR missing mechanism

	True value	θ̂ (ESD)	θ̂ (ESD)	θ̂ (ESD)
		30 Days	90 Days	180 Days
Transition Prob.
γAA	0.90	0.895 (0.0003)	0.894 (0.0011)	0.895 (0.0023)
γAB	0.07	0.070 (0.0003)	0.073 (0.0010)	0.075 (0.0022)
γAE	0.03	0.031 (0.0002)	0.030 (0.0006)	0.030 (0.0010)
γBA	0.03	0.030 (0.0004)	0.030 (0.0013)	0.029 (0.0028)
γBB	0.85	0.840 (0.0008)	0.835 (0.0022)	0.834 (0.0045)
γBC	0.09	0.094 (0.0006)	0.100 (0.0016)	0.109 (0.0032)
γBE	0.03	0.030 (0.0003)	0.030 (0.0009)	0.029 (0.0017)
γCB	0.03	0.029 (0.0006)	0.027 (0.0015)	0.025 (0.0035)
γCC	0.80	0.799 (0.0012)	0.795 (0.0034)	0.795 (0.0071)
γCD	0.14	0.140 (0.0011)	0.144 (0.0031)	0.144 (0.0059)
γCE	0.03	0.033 (0.0003)	0.034 (0.0015)	0.035 (0.0030)
γDC	0.03	0.029 (0.0008)	0.027 (0.0025)	0.023 (0.0051)
γDD	0.75	0.757 (0.0017)	0.763 (0.0042)	0.773 (0.0092)
γDE	0.22	0.213 (0.0015)	0.209 (0.0042)	0.203 (0.0077)

Table 9.

Parameter estimates with MNAR1 missing mechanism

	True value	θ̂(ESD)	θ̂ (ESD)	θ̂ (ESD)
		30 Days	90 Days	180 Days
Transition Prob.
γAA	0.90	0.891 (0.0004)	0.892 (0.0010)	0.894 (0.0019)
γAB	0.07	0.075 (0.0004)	0.076 (0.0010)	0.077 (0.0018)
γAE	0.03	0.030 (0.0002)	0.030 (0.0006)	0.029 (0.0010)
γBA	0.03	0.031 (0.0003)	0.032 (0.0011)	0.032 (0.0025)
γBB	0.85	0.840 (0.0006)	0.838 (0.0020)	0.838 (0.0043)
γBC	0.09	0.092 (0.0005)	0.096 (0.0016)	0.102 (0.0031)
γBE	0.03	0.030 (0.0003)	0.029 (0.0009)	0.029 (0.0017)
γCB	0.03	0.031 (0.0005)	0.031 (0.0016)	0.030 (0.0033)
γCC	0.80	0.803 (0.0011)	0.798 (0.0036)	0.797 (0.0061)
γCD	0.14	0.135 (0.0010)	0.139 (0.0029)	0.140 (0.0059)
γCE	0.03	0.031 (0.0003)	0.032 (0.0011)	0.033 (0.0028)
γDC	0.03	0.031 (0.0008)	0.031 (0.0024)	0.031 (0.0059)
γDD	0.75	0.752 (0.0017)	0.758 (0.0050)	0.768 (0.0092)
γDE	0.22	0.216 (0.0014)	0.211 (0.0039)	0.202 (0.0083)

Table 10.

Parameter estimates with MNAR2 missing mechanism

	True value	θ̂ (ESD)	θ̂ (ESD)	θ̂ (ESD)
		30 Days	90 Days	180 Days
Transition Prob.
γAA	0.90	0.892 (0.0003)	0.892 (0.0011)	0.894 (0.0020)
γAB	0.07	0.074 (0.0003)	0.076 (0.0010)	0.076 (0.0019)
γAE	0.03	0.030 (0.0002)	0.030 (0.0005)	0.029 (0.0010)
γBA	0.03	0.031 (0.0004)	0.032 (0.0013)	0.032 (0.0023)
γBB	0.85	0.837 (0.0007)	0.834 (0.0023)	0.835 (0.0044)
γBC	0.09	0.096 (0.0005)	0.100 (0.0016)	0.105 (0.0033)
γBE	0.03	0.029 (0.0003)	0.029 (0.0009)	0.028 (0.0017)
γCB	0.03	0.030 (0.0005)	0.031 (0.0014)	0.031 (0.0037)
γCC	0.80	0.805 (0.0010)	0.800 (0.0030)	0.798 (0.0069)
γCD	0.14	0.133 (0.0008)	0.137 (0.0029)	0.139 (0.0054)
γ CE	0.03	0.031 (0.0004)	0.032 (0.0014)	0.032 (0.0029)
γDC	0.03	0.031 (0.0007)	0.031 (0.0025)	0.030 (0.0057)
γDD	0.75	0.752 (0.0016)	0.757 (0.0048)	0.768 (0.0099)
γDE	0.22	0.216 (0.0015)	0.212 (0.0042)	0.202 (0.0081)

Table 11.

Parameter estimates with MAR missing mechanism

	True value	θ̂(ESD)	θ̂(ESD)	θ̂(ESD)
		30 Days	90 Days	180 Days
State-dep. Prob.
pA1	0.90	0.905 (0.0019)	0.915 (0.0019)	0.925 (0.0023)
pA2	0.10	0.095 (0.0019)	0.085 (0.0019)	0.075 (0.0023)
pB1	0.10	0.104 (0.0026)	0.112 (0.0037)	0.127 (0.0053)
pB2	0.80	0.830 (0.0028)	0.849 (0.0039)	0.846 (0.0054)
pB3	0.10	0.066 (0.0019)	0.039 (0.0020)	0.027 (0.0025)
pC2	0.10	0.139 (0.0029)	0.191 (0.0052)	0.204 (0.0070)
pC3	0.80	0.800 (0.0035)	0.766 (0.0052)	0.753 (0.0071)
pC4	0.10	0.061 (0.0019)	0.043 (0.0027)	0.043 (0.0046)
pD3	0.10	0.149 (0.0032)	0.172 (0.0061)	0.161 (0.0097)
pD4	0.90	0.851 (0.0032)	0.828 (0.0061)	0.839 (0.0097)

Table 12.

Parameter estimates with MNAR1 missing mechanism

	True value	θ̂(ESD)	θ̂(ESD)	θ̂(ESD)
		30 Days	90 Days	180 Days
State-dep. Prob.
pA1	0.90	0.905 (0.0019)	0.905 (0.0022)	0.906 (0.0024)
pA2	0.10	0.095 (0.0019)	0.095 (0.0022)	0.094 (0.0024)
pB1	0.10	0.105 (0.0023)	0.101 (0.0026)	0.098 (0.0043)
pB2	0.80	0.806 (0.0024)	0.814 (0.0031)	0.825 (0.0043)
pB3	0.10	0.089 (0.0018)	0.085 (0.0023)	0.078 (0.0033)
pC2	0.10	0.099 (0.0021)	0.085 (0.0033)	0.074 (0.0048)
pC3	0.80	0.814 (0.0026)	0.840 (0.0039)	0.856 (0.0055)
pC4	0.10	0.087 (0.0018)	0.075 (0.0027)	0.070 (0.0050)
pD3	0.10	0.106 (0.0028)	0.103 (0.0052)	0.095 (0.0091)
pD4	0.90	0.894 (0.0028)	0.897 (0.0052)	0.905 (0.0091)

Table 16.

Parameter estimates for the CKD data: 90 Day

	Women	Men
	Estimate (SE)	Estimate (SE)
Transition Prob.
γAA	0.987 (0.0004)	0.989 (0.0004)
γAB	0.011 (0.0004)	0.009 (0.0004)
γ AF	0.002 (0.0001)	0.002 (0.0001)
γBA	0.029 (0.0015)	0.025 (0.0025)
γBB	0.932 (0.0024)	0.928 (0.0037)
γBC	0.036 (0.0019)	0.038 (0.0020)
γBF	0.003 (0.0004)	0.009 (0.0007)
γCB	0.014 (0.0008)	0.016 (0.0018)
γCC	0.973 (0.0009)	0.962 (0.0019)
γCD	0.007 (0.0005)	0.011 (0.0006)
γCF	0.006 (0.0004)	0.011 (0.0007)
γDC	0.031 (0.0043)	0.029 (0.0046)
γ DD	0.918 (0.0051)	0.896 (0.0057)
γDE	0.016 (0.0019)	0.026 (0.0036)
γDF	0.035 (0.0033)	0.049 (0.0052)
γED	0.000 (0.0000)	0.033 (0.0152)
γEE	0.839 (0.0329)	0.704 (0.0303)
γEF	0.161 (0.0329)	0.263 (0.0311)

Appendix. Formulas

Likelihood

Let’s assume the hidden state, h_it, where i = 1, ..., N and t = 1, ..., T_i, takes on a discrete value, s, from a sample space, S, such that, s = 1, ..., S. The observed state, y_it, can also take on a discrete value, m, from a sample space, M, such that, m = 1, ..., M . At time t and given the hidden state, h_it, y_it can be observed from a state-dependent probability distribution.

$$\begin{array}{l}L\left(\theta |Y,H\right)\propto \prod _{i=1}^N\prod _{j=A}^E{\pi }_j^{I\left(h_{i1}=j\right)}\times \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\prod _{i=1}^N\prod _{t=2}^{T_i}\prod _{j=A}^E\prod _{k=A}^E{\gamma }_{jk}^{I\left(h_{\mathit{it}-1}=j\right)I\left(h_{\mathit{it}}=k\right)}\times \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\prod _{i=1}^N\prod _{t=1}^{T_i}\prod _{j=A}^E\prod _{k=1}^M{p}_{jk}^{I\left(h_{\mathit{it}}=j\right)I\left(y_{\mathit{it}}=k\right)}\end{array}$$

From the likelihood above, we can see that given the hidden states, the initial state probability, the transition probability, and the state dependent probability have multinomial distributions with parameter π, γ_jk, and p_jk . To simplify the estimation of the parameters, the log of this augmented likelihood is often used.

$$\begin{array}{l}l\left(\theta |Y,H,Z\right)\propto \sum _{i=1}^n\sum _{j=A}^{E}I\left(h_{i1}=j\right)\text{log}\left({\pi }_j\right)+\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\sum _{i=1}^n\sum _{t=2}^{T_i}\sum _{j=A}^E\sum _{k=A}^{E}I\left(h_{\mathit{it}-1}=j\right)I\left(h_{\mathit{it}}=k\right)\text{log}\left({\gamma }_{jk}\right)+\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\sum _{i=1}^n\sum _{t=1}^{T_i}\sum _{j=A}^E\sum _{k=1}^{M}I\left(h_{\mathit{it}}=j\right)I\left(y_{\mathit{it}}=k\right)\text{log}\left(p_{jk}\right)\end{array}$$

Expectation Maximization (EM) Method

To estimate the parameters, θ, an iterative algorithm called the “expected-maximization (EM) algorithm” is used. The EM algorithm is an iterative algorithm in which iteratively, the expected value of the complete data log likelihood given the current parameters is computed (E-step) and then this expected value is maximized over the parameters (M-step). The special case of the EM algorithm for HMMs was developed by Baum and Welch (1970). For the E-step, the forward-backward (FB) algorithm is used. This algorithm is composed of two passes: the forward and the backward (MacDonald and Zucchini 1997). In the forward pass, the joint distribution of the observed data up to time t and the hidden state at time t is calculated. After all the data are observed, the backward pass will update the information on the hidden state from the last time point to the first based on all the observed data. In the forward pass, denoted by α_t, the joint distribution of the observed data up to time t and the hidden state at time t is calculated as below:

$$\begin{array}{lll}\hfill {\alpha }_t(i)& =\hfill & \text{Pr}\left(Y_1=y_1,\dots ,Y_t=y_t,H_t=i\right)\hfill \\ \hfill {\alpha }_1(i)& =& \text{Pr}\left(H_1=i\right)\text{Pr}\left(Y_1=y_1|H_1=i\right)={\pi }_i{P}_{1,y1}\hfill \\ \hfill {\alpha }_{t+1}(j)& =& \sum _{i=A}^E\text{Pr}\left(Y_1,\dots ,Y_{t+1},H_t=i,H_{t+1}=j\right)\hfill \\ & =\hfill & \left(\sum _{i=A}^E{\alpha }_t(i){\gamma }_{ij}\right)P_{t+1,y_{t+1}}\hfill \end{array}$$

After all the data are observed, the backward pass, β_t, will update the information on the hidden state from the last time point to the first based on all the observed data.

$$\begin{array}{lll}{\beta }_t(i)\hfill & =\hfill & \text{Pr}\left(Y_{t+1}=y_{t+1},\dots ,Y_T=y_T|H_t=i\right)\hfill \\ {\beta }_T(i)\hfill & =\hfill & 1\hfill \\ {\beta }_t(i)\hfill & =\hfill & \sum _{j=A}^E\frac{\text{Pr}\left(Y_{t+1},\dots ,Y_{T,}{H}_t=i,H_{t+1}=j\right)}{\text{Pr}\left(H_t=i\right)}\hfill \\ \hfill & =\hfill & \sum _{j=A}^E{\beta }_{t+1}(j){\gamma }_{ij}{P}_{t+1,y_{t+1}}\hfill \end{array}$$

The observed likelihood for each subject, i, can be calculated using α_i in the following way:

$$\begin{array}{lll}\hfill L_{\mathit{iT}}& =\hfill & \sum _{j=A}^E\text{Pr}\left(Y_{i1}=y_{i1},\dots ,Y_{\mathit{iT}},H_{\mathit{iT}}=j\right)\hfill \\ \hfill & =\hfill & \sum _{j=A}^E{\alpha }_{\mathit{iT}}(j)\hfill \end{array}$$

Since there are hidden data, H, in the log likelihood, we use the expected value of the missing information to compute the expected value of the complete data log likelihood given the current parameter estimates:

$$\begin{array}{lll}E\left[l\left(\theta |Y,H\right)\right]\hfill & \propto \hfill & \text{log}\left({\pi }_i\right)\sum _{i=1}^n\sum _{j=A}^{E}E\left[I\left(h_{i1}=j\right)\right]+\hfill \\ \hfill & \hfill & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{log}\left({\gamma }_{jk}\right)\sum _{i=1}^n\sum _{t=2}^{T_i}\sum _{j=A}^E\sum _{k=A}^{E}E\left[I\left(h_{\mathit{it}-1}=k\right)\right]+\hfill \\ \hfill & \hfill & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{log}\left(p_{\mathit{jk}}\right)\sum _{i=1}^n\sum _{t=1}^{T_i}\sum _{j=A}^E\sum _{k=1}^{M}I\left(y_{\mathit{it}}=k\right)E\left[I\left(h_{\mathit{it}}=j\right)\right]\hfill \end{array}$$

The expectation of the missing data are calculated as follows. Note the superfix g represents the gth iteration of the parameters.

$$E\left[I\left(h_{i1}=j\right)|Y,{\theta }^g\right]=\frac{{\alpha }_{i1}^g(j){\beta }_{i1}^g(j)}{L_{\mathit{iT}}}$$

$$E\left[I\left(h_{\mathit{it}}=j\right)|Y,{\theta }^g\right]=\frac{{\alpha }_{\mathit{it}}^g(j){\beta }_{\mathit{it}}^g(j)}{L_{\mathit{iT}}}$$

$$E\left[I\left(h_{\mathit{it}}=k\right)I\left(h_{\mathit{it}-1}=j\right)|Y,{\theta }^g\right]=\frac{{\alpha }_{\mathit{it}-1}^g(j){\gamma }_{\mathit{jk}}{P}_{t,y_t}{\beta }_{\mathit{it}}^g(k)}{L_{iT}}$$

In the M-step, θ can be estimated in closed form using the expected values derived from above.

The initial probability distribution, π, can be estimated as follows:

$${\widehat{\pi }}^{g+1}(j)=\frac{\sum E\left[I\left(h_{i1}=j\right)|Y,{\theta }^g\right]}{n}$$

The transition probability, γ_ij, where i = 1, ...S, j = 1, ..., S, can be estimated as follow:

$${\widehat{\gamma }}_{\mathit{jk}}^{g+1}=\frac{{\sum }_{i=1}^n{\sum }_{t=2}^{T_i}E\left[I\left(h_{\mathit{it}}=k\right)I\left(h_{\mathit{it}-1}=j\right)|Y,{\theta }^g\right]}{{\sum }_{i=1}^n{\sum }_{t=2}^{T_i}E\left[I\left(h_{\mathit{it}-1}=j\right)|Y,{\theta }^g\right]}$$

The state dependent probability, p_jk, where j = 1, ...S, k = 1, ..., M, can be estimated as follow:

$${\widehat{p}}_{jk}^{g+1}=\frac{{\sum }_{i=1}^n{\sum }_{t=1}^{T_i}I\left(y_{\mathit{it}}=k\right)E\left[I\left(h_{\mathit{it}}=j\right)z_{\mathit{it}}|Y,{\theta }^g\right]}{{\sum }_{j=1}^M{\sum }_{i=1}^n{\sum }_{t=1}^{T_i}I\left(y_{\mathit{it}}=k\right)E\left[I\left(h_{\mathit{it}}=j\right)z_{\mathit{it}}|Y,{\theta }^g\right]}$$

The EM method does not provide the standard errors for the parameters. We have decided to estimate the standard errors using bootstrap with replacement.

How to Handle Missing Data

If data is missing at a particular time point, an empty transition is assumed to occur. This is illustrated by replacing the state dependent probability, P_s,yt,with 1’s in the calculation of α_t, β_t, and E[I (h_it = k)I (h_it−1 = j)].

$${\alpha }_t(i)=\left(\sum _{i=A}^E{\alpha }_t(i){\gamma }_{ij}\right)\times 1$$

$${\beta }_t(i)=\sum _{j=A}^E{\beta }_{t+1}(j){\gamma }_{ij}\times 1$$

$$E\left[I\left(h_{\mathit{it}}=k\right)I\left(h_{\mathit{it}-1}=j\right)|Y,{\theta }^g\right]=\frac{{\alpha }_{\mathit{it}-1}^g(j){\gamma }_{jk}\times 1\times {\beta }_{\mathit{it}}^g(k)}{L_{\mathit{iT}}}$$

Simulation Results: Scheme 2

Table 18.

The average computation time (seconds)

Missing Mechanism	30 Day	90 Day	180 Day
MAR	9643	2657	1568
MNAR1	14036	2490	1513
MNAR2	14941	2760	2254

Table 19.

Parameter estimates with MAR missing mechanism

	True value	θ̂(ESD)	θ̂(ESD)	θ̂(ESD)
		30 Days	90 Days	180 Days
Initial Prob.
πA	0.80	0.799 (0.007)	0.794 (0.006)	0.775 (0.006)
πB	0.10	0.103 (0.005)	0.109 (0.005)	0.127 (0.006)
πC	0.07	0.069 (0.004)	0.068 (0.004)	0.068 (0.004)
πD	0.03	0.029 (0.002)	0.030 (0.002)	0.030 (0.002)

Table 20.

Parameter estimates with MAR missing mechanism

	True value	θ̂(ESD)	θ̂(ESD)	θ̂(ESD)
		30 Days	90 Days	180 Days
Transition Prob.
γAA	0.90	0.895 (0.0004)	0.894 (0.0011)	0.895 (0.0020)
γAB	0.07	0.071 (0.0003)	0.073 (0.0011)	0.075 (0.0017)
γAE	0.03	0.031 (0.0002)	0.031 (0.0005)	0.030 (0.0010)
γBA	0.03	0.030 (0.0005)	0.030 (0.0014)	0.029 (0.0027)
γBB	0.85	0.840 (0.0007)	0.836 (0.0021)	0.834 (0.0046)
γBC	0.09	0.094 (0.0005)	0.100 (0.0017)	0.109 (0.0032)
γBE	0.03	0.029 (0.0003)	0.029 (0.0009)	0.029 (0.0018)
γCB	0.03	0.029 (0.0006)	0.027 (0.0016)	0.026 (0.0037)
γCC	0.80	0.799 (0.0011)	0.795 (0.0036)	0.795 (0.0066)
γCD	0.14	0.139 (0.0009)	0.144 (0.0030)	0.145 (0.0058)
γCE	0.03	0.033 (0.0004)	0.034 (0.0013)	0.035 (0.0035)
γDC	0.03	0.030 (0.0007)	0.028 (0.0024)	0.025 (0.0053)
γDD	0.75	0.757 (0.0017)	0.762 (0.0045)	0.772 (0.0092)
γDE	0.22	0.213 (0.0015)	0.210 (0.0041)	0.203 (0.0085)

Table 21.

Parameter estimates with MAR missing mechanism

	True value	θ̂(ESD)	θ̂(ESD)	θ̂(ESD)
		30 Days	90 Days	180 Days
State-dep. Prob.
pA1	0.90	0.905 (0.0017)	0.915 (0.0018)	0.925 (0.0023)
pA2	0.10	0.095 (0.0017)	0.085 (0.0018)	0.075 (0.0023)
pB1	0.10	0.104 (0.0026)	0.112 (0.0032)	0.126 (0.0047)
pB2	0.80	0.830 (0.0030)	0.849 (0.0033)	0.846 (0.0053)
pB3	0.10	0.066 (0.0018)	0.039 (0.0018)	0.027 (0.0025)
pC2	0.10	0.139 (0.0023)	0.191 (0.0046)	0.203 (0.0078)
pC3	0.80	0.800 (0.0028)	0.766 (0.0045)	0.754 (0.0073)
pC4	0.10	0.061 (0.0017)	0.043 (0.0028)	0.043 (0.0046)
pD3	0.10	0.149 (0.0030)	0.173 (0.0058)	0.159 (0.0092)
pD4	0.90	0.851 (0.0030)	0.827 (0.0058)	0.841 (0.0092)

Table 22.

Parameter estimates with MNAR1 missing mechanism

	True value	θ̂(ESD)	θ̂(ESD)	θ̂(ESD)
		30 Days	90 Days	180 Days
Initial Prob.
πA	0.80	0.787 (0.006)	0.778 (0.007)	0.754 (0.006)
πB	0.10	0.109 (0.005)	0.120 (0.006)	0.143 (0.005)
πC	0.07	0.073 (0.003)	0.071 (0.004)	0.071 (0.004)
πD	0.03	0.031 (0.002)	0.031 (0.003)	0.032 (0.003)

Table 23.

Parameter estimates with MNAR1 missing mechanism

	True value	θ̂(ESD)	θ̂(ESD)	θ̂(ESD)
		30 Days	90 Days	180 Days
Transition Prob.
γAA	0.90	0.891 (0.0004)	0.892 (0.0010)	0.895 (0.0021)
γAB	0.07	0.075 (0.0003)	0.076 (0.0009)	0.076 (0.0019)
γAE	0.03	0.030 (0.0002)	0.030 (0.0006)	0.029 (0.0011)
γBA	0.03	0.031 (0.0004)	0.032 (0.0011)	0.031 (0.0024)
γBB	0.85	0.840 (0.0008)	0.838 (0.0020)	0.838 (0.0045)
γBC	0.09	0.092 (0.0006)	0.096 (0.0015)	0.103 (0.0034)
γBE	0.03	0.030 (0.0003)	0.030 (0.0009)	0.029 (0.0017)
γCB	0.03	0.030 (0.0005)	0.031 (0.0017)	0.031 (0.0032)
γCC	0.80	0.804 (0.0011)	0.796 (0.0033)	0.796 (0.0063)
γCD	0.14	0.135 (0.0010)	0.140 (0.0028)	0.141 (0.0055)
γCE	0.03	0.031 (0.0003)	0.033 (0.0011)	0.033 (0.0031)
γDC	0.03	0.031 (0.0007)	0.031 (0.0021)	0.030 (0.0049)
γDD	0.75	0.752 (0.0017)	0.756 (0.0043)	0.767 (0.0099)
γDE	0.22	0.217 (0.0016)	0.213 (0.0038)	0.203 (0.0084)

Table 24.

Parameter estimates with MNAR1 missing mechanism

	True value	θ̂(ESD)	θ̂(ESD)	θ̂(ESD)
		30 Days	90 Days	180 Days
State-dep. Prob.
pA1	0.90	0.905 (0.0017)	0.905 (0.0020)	0.906 (0.0024)
pA2	0.10	0.095 (0.0017)	0.095 (0.0020)	0.094 (0.0024)
pB1	0.10	0.104 (0.0022)	0.100 (0.0026)	0.099 (0.0034)
pB2	0.80	0.806 (0.0028)	0.814 (0.0030)	0.823 (0.0035)
pB3	0.10	0.090 (0.0020)	0.086 (0.0024)	0.078 (0.0032)
pC2	0.10	0.099 (0.0020)	0.085 (0.0031)	0.074 (0.0047)
pC3	0.80	0.814 (0.0027)	0.840 (0.0036)	0.855 (0.0056)
pC4	0.10	0.087 (0.0018)	0.075 (0.0027)	0.071 (0.0050)
pD3	0.10	0.105 (0.0028)	0.103 (0.0046)	0.093 (0.0083)
pD4	0.90	0.895 (0.0028)	0.897 (0.0046)	0.907 (0.0083)

Table 25.

Parameter estimates with MNAR2 missing mechanism

	True value	θ̂(ESD)	θ̂(ESD)	θ̂(ESD)
		30 Days	90 Days	180 Days
Initial Prob.
πA	0.80	0.791 (0.006)	0.781 (0.006)	0.757 (0.006)
πB	0.10	0.105 (0.005)	0.116 (0.005)	0.139 (0.005)
πC	0.07	0.073 (0.004)	0.072 (0.004)	0.072 (0.004)
πD	0.03	0.031 (0.002)	0.031 (0.002)	0.032 (0.003)

Table 26.

Parameter estimates with MNAR2 missing mechanism

	True value	θ̂(ESD)	θ̂(ESD)	θ̂(ESD)
		30 Days	90 Days	180 Days
Transition Prob.
γAA	0.90	0.892 (0.0004)	0.892 (0.0010)	0.894 (0.0021)
γAB	0.07	0.074 (0.0003)	0.076 (0.0009)	0.077 (0.0017)
γAE	0.03	0.030 (0.0002)	0.032 (0.0005)	0.029 (0.0011)
γBA	0.03	0.032 (0.0004)	0.032 (0.0012)	0.032 (0.0027)
γBB	0.85	0.836 (0.0008)	0.835 (0.0024)	0.835 (0.0042)
γBC	0.09	0.096 (0.0005)	0.100 (0.0019)	0.106 (0.0030)
γBE	0.03	0.036 (0.0003)	0.033 (0.0010)	0.027 (0.0018)
γCB	0.03	0.030 (0.0004)	0.031 (0.0017)	0.031 (0.0033)
γCC	0.80	0.805 (0.0010)	0.800 (0.0035)	0.796 (0.0064)
γCD	0.14	0.133 (0.0009)	0.137 (0.0030)	0.140 (0.0048)
γCE	0.03	0.032 (0.0003)	0.032 (0.0012)	0.033 (0.0030)
γDC	0.03	0.031 (0.0008)	0.031 (0.0026)	0.031 (0.0057)
γDD	0.75	0.752 (0.0017)	0.756 (0.0053)	0.766 (0.0085)
γDE	0.22	0.217 (0.0015)	0.213 (0.0047)	0.203 (0.0074)

Table 27.

Parameter estimates with MNAR2 missing mechanism

	True value	θ̂ (ESD)	θ̂ (ESD)	θ̂ (ESD)
		30 Days	90 Days	180 Days
State-dep. Prob.
pA1	0.90	0.904 (0.0018)	0.904 (0.0019)	0.905 (0.0024)
pA2	0.10	0.096 (0.0018)	0.096 (0.0019)	0.095 (0.0024)
pB1	0.10	0.104 (0.0021)	0.102 (0.0031)	0.103 (0.0044)
pB2	0.80	0.805 (0.0026)	0.809 (0.0034)	0.815 (0.0050)
pB3	0.10	0.091 (0.0020)	0.089 (0.0026)	0.082 (0.0032)
pC2	0.10	0.097 (0.0019)	0.084 (0.0033)	0.073 (0.0047)
pC3	0.80	0.813 (0.0023)	0.838 (0.0038)	0.854 (0.0054)
pC4	0.10	0.090 (0.0019)	0.078 (0.0029)	0.073 (0.0046)
pD3	0.10	0.101 (0.0023)	0.099 (0.0049)	0.090 (0.0072)
pD4	0.90	0.899 (0.0023)	0.901 (0.0049)	0.910 (0.0072)

Simulation Results: Scheme 3

Table 28.

The average computation time (seconds)

Missing Mechanism	30 Day	90 Day	180 Day
MAR	9359	2682	1560
MNAR1	8631	3574	2125
MNAR2	9864	2703	1592

Table 29.

Parameter estimates with MAR missing mechanism

	True value	θ̂(ESD)	θ̂(ESD)	θ̂(ESD)
		30 Days	90 Days	180 Days
Initial Prob.
πA	0.80	0.799 (0.006)	0.794 (0.006)	0.773 (0.007)
πB	0.10	0.102 (0.006)	0.108 (0.005)	0.128 (0.006)
πC	0.07	0.069 (0.004)	0.068 (0.004)	0.068 (0.004)
πD	0.03	0.030 (0.002)	0.030 (0.002)	0.031 (0.002)

Table 30.

Parameter estimates with MAR missing mechanism

	True value	θ̂(ESD)	θ̂(ESD)	θ̂(ESD)
		30 Days	90 Days	180 Days
Transition Prob.
γAA	0.90	0.895 (0.0003)	0.895 (0.0011)	0.895 (0.0022)
γAB	0.07	0.071 (0.0003)	0.073 (0.0009)	0.075 (0.0018)
γAE	0.03	0.031 (0.0002)	0.032 (0.0005)	0.030 (0.0010)
γBA	0.03	0.030 (0.0004)	0.030 (0.0014)	0.029 (0.0029)
γBB	0.85	0.840 (0.0007)	0.835 (0.0022)	0.833 (0.0044)
γBC	0.09	0.093 (0.0005)	0.101 (0.0016)	0.109 (0.0031)
γBE	0.03	0.037 (0.0003)	0.029 (0.0010)	0.029 (0.0019)
γCB	0.03	0.029 (0.0005)	0.027 (0.0018)	0.026 (0.0030)
γCC	0.80	0.799 (0.0010)	0.793 (0.0039)	0.795 (0.0066)
γCD	0.14	0.140 (0.0009)	0.145 (0.0031)	0.144 (0.0054)
γCE	0.03	0.032 (0.0004)	0.034 (0.0013)	0.035 (0.0031)
γDC	0.03	0.029 (0.0007)	0.029 (0.0023)	0.026 (0.0048)
γDD	0.75	0.758 (0.0017)	0.762 (0.0047)	0.773 (0.0090)
γDE	0.22	0.213 (0.0016)	0.209 (0.0040)	0.201 (0.0080)

Table 31.

Parameter estimates with MAR missing mechanism

	True value	θ̂(ESD)	θ̂(ESD)	θ̂(ESD)
		30 Days	90 Days	180 Days
State-dep. Prob.
pA1	0.90	0.906 (0.0019)	0.914 (0.0019)	0.925 (0.0025)
pA2	0.10	0.094 (0.0019)	0.086 (0.0019)	0.075 (0.0025)
pB1	0.10	0.104 (0.0023)	0.112 (0.0032)	0.126 (0.0047)
pB2	0.80	0.830 (0.0026)	0.849 (0.0036)	0.847 (0.0048)
pB3	0.10	0.066 (0.0018)	0.039 (0.0022)	0.027 (0.0023)
pC2	0.10	0.139 (0.0024)	0.191 (0.0048)	0.203 (0.0069)
pC3	0.80	0.800 (0.0028)	0.766 (0.0046)	0.755 (0.0073)
pC4	0.10	0.061 (0.0018)	0.043 (0.0024)	0.042 (0.0040)
pD3	0.10	0.149 (0.0029)	0.172 (0.0054)	0.160 (0.0115)
pD4	0.90	0.851 (0.0029)	0.828 (0.0054)	0.840 (0.0115)

Table 32.

Parameter estimates with MNAR1 missing mechanism

	True value	θ̂(ESD)	θ̂(ESD)	θ̂(ESD)
		30 Days	90 Days	180 Days
Initial Prob.
πA	0.80	0.788 (0.007)	0.778 (0.007)	0.754 (0.007)
πB	0.10	0.109 (0.005)	0.120 (0.006)	0.143 (0.006)
πC	0.07	0.073 (0.003)	0.071 (0.004)	0.071 (0.004)
πD	0.03	0.030 (0.003)	0.031 (0.002)	0.032 (0.003)

Table 33.

Parameter estimates with MNAR1 missing mechanism

	True value	θ̂(ESD)	θ̂(ESD)	θ̂(ESD)
		30 Days	90 Days	180 Days
Transition Prob.
γAA	0.90	0.891 (0.0004)	0.892 (0.0012)	0.894 (0.0019)
γAB	0.07	0.075 (0.0004)	0.076 (0.0010)	0.077 (0.0018)
γAE	0.03	0.034 (0.0002)	0.032 (0.0005)	0.029 (0.0011)
γBA	0.03	0.031 (0.0004)	0.031 (0.0013)	0.031 (0.0025)
γBB	0.85	0.841 (0.0007)	0.838 (0.0022)	0.838 (0.0039)
γBC	0.09	0.092 (0.0005)	0.097 (0.0015)	0.102 (0.0030)
γBE	0.03	0.036 (0.0003)	0.034 (0.0010)	0.029 (0.0018)
γCB	0.03	0.031 (0.0005)	0.030 (0.0017)	0.030 (0.0035)
γCC	0.80	0.802 (0.0010)	0.799 (0.0030)	0.797 (0.0061)
γCD	0.14	0.136 (0.0009)	0.138 (0.0026)	0.140 (0.0051)
γCE	0.03	0.031 (0.0003)	0.033 (0.0013)	0.033 (0.0032)
γDC	0.03	0.031 (0.0007)	0.031 (0.0023)	0.030 (0.0050)
γDD	0.75	0.755 (0.0015)	0.756 (0.0049)	0.768 (0.0085)
γDE	0.22	0.214 (0.0014)	0.213 (0.0040)	0.202 (0.0076)

Table 34.

Parameter estimates with MNAR1 missing mechanism

	True value	θ̂(ESD)	θ̂(ESD)	θ̂(ESD)
		30 Days	90 Days	180 Days
State-dep. Prob.
pA1	0.90	0.905 (0.0017)	0.905 (0.0021)	0.906 (0.0025)
pA2	0.10	0.095 (0.0017)	0.095 (0.0021)	0.094 (0.0025)
pB1	0.10	0.104 (0.0020)	0.101 (0.0030)	0.098 (0.0042)
pB2	0.80	0.807 (0.0026)	0.814 (0.0037)	0.823 (0.0042)
pB3	0.10	0.089 (0.0019)	0.085 (0.0026)	0.078 (0.0033)
pC2	0.10	0.099 (0.0019)	0.085 (0.0030)	0.075 (0.0043)
pC3	0.80	0.814 (0.0022)	0.840 (0.0035)	0.856 (0.0054)
pC4	0.10	0.087 (0.0018)	0.075 (0.0029)	0.069 (0.0042)
pD3	0.10	0.105 (0.0027)	0.103 (0.0043)	0.095 (0.0087)
pD4	0.90	0.895 (0.0027)	0.897 (0.0043)	0.905 (0.0087)

Table 35.

Parameter estimates with MNAR2 missing mechanism

	True value	θ̂(ESD)	θ̂(ESD)	θ̂(ESD)
		30 Days	90 Days	180 Days
Initial Prob.
πA	0.80	0.791 (0.006)	0.781 (0.007)	0.757 (0.006)
πB	0.10	0.106 (0.005)	0.115 (0.006)	0.139 (0.005)
πC	0.07	0.073 (0.003)	0.072 (0.004)	0.071 (0.004)
πD	0.03	0.030 (0.002)	0.032 (0.003)	0.033 (0.003)

Table 36.

Parameter estimates with MNAR2 missing mechanism

	True value	θ̂(ESD)	θ̂(ESD)	θ̂(ESD)
		30 Days	90 Days	180 Days
Transition Prob.
γAA	0.90	0.892 (0.0004)	0.892 (0.0010)	0.895 (0.0021)
γAB	0.07	0.074 (0.0003)	0.076 (0.0009)	0.076 (0.0020)
γAE	0.03	0.030 (0.0002)	0.032 (0.0005)	0.029 (0.0011)
γBA	0.03	0.032 (0.0004)	0.032 (0.0012)	0.032 (0.0027)
γBB	0.85	0.837 (0.0007)	0.835 (0.0024)	0.835 (0.0044)
γBC	0.09	0.096 (0.0005)	0.100 (0.0017)	0.105 (0.0032)
γBE	0.03	0.035 (0.0003)	0.033 (0.0008)	0.028 (0.0016)
γCB	0.03	0.030 (0.0005)	0.031 (0.0015)	0.031 (0.0038)
γCC	0.80	0.805 (0.0011)	0.799 (0.0029)	0.796 (0.0063)
γCD	0.14	0.134 (0.0010)	0.137 (0.0026)	0.140 (0.0053)
γCE	0.03	0.031 (0.0004)	0.032 (0.0012)	0.033 (0.0025)
γDC	0.03	0.030 (0.0007)	0.030 (0.0026)	0.031 (0.0054)
γDD	0.75	0.752 (0.0016)	0.756 (0.0047)	0.766 (0.0093)
γDE	0.22	0.218 (0.0013)	0.214 (0.0045)	0.203 (0.0077)

Table 37.

Parameter estimates with MNAR2 missing mechanism

	True value	θ̂(ESD)	θ̂(ESD)	θ̂(ESD)
		30 Days	90 Days	180 Days
State-dep. Prob.
pA1	0.90	0.904 (0.0017)	0.904 (0.0018)	0.906 (0.0025)
pA2	0.10	0.096 (0.0017)	0.096 (0.0018)	0.094 (0.0025)
pB1	0.10	0.104 (0.0026)	0.101 (0.0033)	0.102 (0.0042)
pB2	0.80	0.805 (0.0027)	0.810 (0.0039)	0.816 (0.0045)
pB3	0.10	0.091 (0.0019)	0.088 (0.0029)	0.082 (0.0035)
pC2	0.10	0.097 (0.0021)	0.083 (0.0028)	0.073 (0.0052)
pC3	0.80	0.813 (0.0025)	0.838 (0.0039)	0.854 (0.0061)
pC4	0.10	0.090 (0.0020)	0.079 (0.0030)	0.073 (0.0048)
pD3	0.10	0.101 (0.0023)	0.099 (0.0051)	0.090 (0.0082)
pD4	0.90	0.899 (0.0023)	0.901 (0.0051)	0.910 (0.0082)