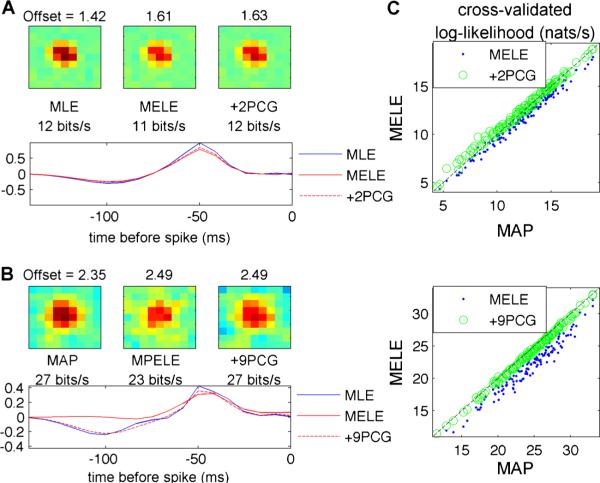
Fig. 3.

The MPELE provides a good initializer for finding approximate MAP estimators using fast gradient-based optimization methods in the LNP model. a The spatiotemporal receptive field of a typical retinal ganglion cell (RGC) in our database responding to binary white-noise stimuli and fit with a linear-nonlinear Poisson (LNP) model with exponential non-linearity, via the MLE. The receptive field of the same cell fit using the MELE is also plotted. The goodness-offit of the MLE (measured in terms of cross-validated log-likelihood; see Appendix) is slightly higher than that of the MELE (12 versus 11 bits/s). However, this difference disappears after a couple pre-conditioned conjugate gradient (PCG) iterations using the true likelihood initialized at the MELE (see label +2PCG). Note that we are only showing representative spatial and temporal slices of the 9×9×10 dimensional receptive field, for clarity. b Similar results hold when the same cell responds to 1/f correlated Gaussian noise stimuli (for correlated Gaussian responses, the MAP and MPELE are both fit with a ridge penalty). In this case 9 PCG iterations sufficed to compute an estimator with a goodness-of-fit equal to that of the MAP. c These results are consistent over the observed population. (top) Scatterplot of cross-validated log-likelihood across a population of 91 cells, responding to binary white-noise stimuli, each fit independently using the MLE, MELE or a couple PCG iterations using the true likelihood and initialized at the MELE. (bottom) Log-likelihood for the same population, responding to 1/f Gaussian noise, fit independently using an L2 regularized MAP, MPELE or 9 PCG iterations using the true regularized likelihood initialized at the MPELE