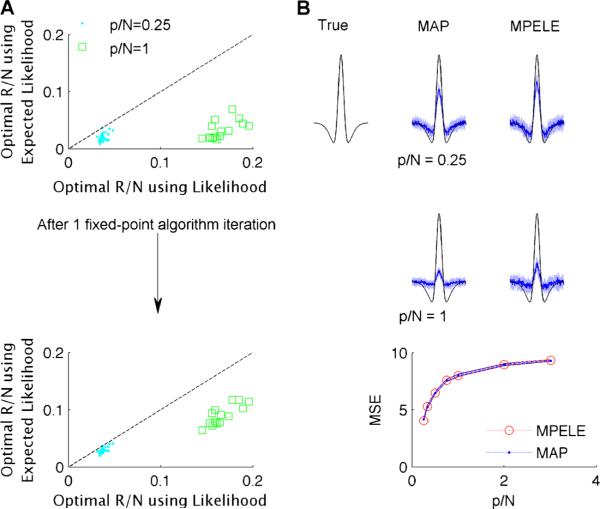
Fig. 5.
The EL can be used for fast model selection via approximate maximum marginal likelihood. Thirty simulated neural responses were drawn from a linear-nonlinear Poisson (LNP) model, with stimuli drawn from an independent white-noise Gaussian distribution. The true filter (shown in black in B) has p = 250 parameters and norm 10. a Optimal hyper-parameters R (the precision of the Gaussian prior distribution) which maximize the marginal likelihood using the EL (top left column, vertical axis) scale similarly to those which maximize the full Laplace-approximated marginal likelihood (top left column, horizontal axis), but with a systematic downward bias. After a single iteration of the fixed point algorithm used to maximize the full marginal likelihood (see text), the two sets of hyper-parameters (bottom left column) match to what turns out to be sufficient accuracy, as shown in (b): the median filter estimates (blue lines) (± absolute median deviation (light blue), based on 30 replications) computed using the exact and one-step approximate approach match for a wide range of . The MSE of the two approaches also matches for a wide range of