Replicability and Robustness of GWAS for Behavioral Traits

Abstract

A recent genome-wide association study (GWAS) of educational attainment identified three single-nucleotide polymorphisms (SNPs) that, despite their small effect sizes (each R² ≈ 0.02%), reached genome-wide significance (p < 5×10⁻⁸) in a large discovery sample and replicated in an independent sample (p < 0.05). The study also reported associations between educational attainment and indices of SNPs called “polygenic scores.” We evaluate the robustness of these findings. Study 1 finds that all three SNPs replicate in another large (N = 34,428) independent sample. We also find that the scores remain predictive (R² ≈ 2%) with stringent controls for stratification (Study 2) and in new within-family analyses (Study 3). Our results show that large and therefore well-powered GWASs can identify replicable genetic associations with behavioral traits. The small effect sizes of individual SNPs are likely to be a major contributing explanation for the striking contrast between our results and the disappointing replication record of most candidate gene studies.

Introduction

The discovery of genetic variants associated with behavioral traits could eventually be transformative for the social sciences, but the first step is identifying the specific genes associated with a trait. In psychology, the standard approach is the “candidate gene study.” In a candidate gene study, a small set of genetic variants (“polymorphisms”) is selected based on their hypothesized or known biological function, and these polymorphisms are tested for association with the trait. Most candidate gene studies are based on samples of several hundred participants and apply a significance threshold of 0.05 (for a review, see Ebstein, Israel, Chew, Zhong, & Knafo, 2010).

Despite the fact that such studies continue to be published in prominent journals, the successful replication of published genetic associations with behavioral traits is the exception, not the rule (Benjamin et al., 2012; Hewitt, 2012). In fact, the situation is so alarming that the editor of the leading field journal Behavior Genetics recently issued an editorial policy on candidate gene studies of behavioral traits that began “The literature on candidate gene associations is full of reports that have not stood up to rigorous replication” and went on to say “…it now seems likely that many of the published findings of the last decade are wrong or misleading and have not contributed to real advances in knowledge” (Hewitt, 2012). Psychological Science has adopted the same strict standards for evaluating candidate-gene studies.

Why the findings from candidate gene studies of complex behaviors replicate inconsistently remains an open question, but it is commonly believed that low statistical power is a major contributing factor, and that the problem of low power is further compounded if the reported p-values correct for only a subset of the multiple hypotheses that were tested (Hewitt, 2012; Ioannidis, 2005). Candidate gene studies also cannot always adequately control for the well-known problem of “population stratification”: genotypes may covary with unobserved environmental factors (Hamer & Sirota, 2000). For example, individuals with shared genetic ancestry (say, from the same ethnic group or from the same ancestral region) may also be more likely to share values, cultural practices, or exposure to other unobserved environmental confounds. Population stratification can give rise to associations driven by the shared environmental factors but spuriously attributed to the shared genotype (Cardon and Palmer, 2003). A finding may be confounded by population stratification even though it successfully replicates if the population structure that caused a spurious genetic discovery is also present in the replication samples.

As a result of the methodological limitations of candidate gene studies and the dramatic decline in the cost of genotyping, a paradigm shift took place around 2005 in medical research away from candidate gene studies to what are called “genome-wide association studies” (GWAS) (McCarthy et al., 2008; Pearson & Manolio, 2008; Visscher, Brown, McCarthy, & Yang, 2012). These are hypothesis-free studies in which researchers test the phenotype of interest for association with all of the (typically millions of) measured single-nucleotide polymorphisms (SNPs). Because of the large number of hypotheses tested, an association is only considered established if the SNP (i) reaches the “genome-wide significance” threshold of p < 5×10⁻⁸, and (ii) is subsequently successfully replicated in an independent sample at a nominal significance level of 0.05 (McCarthy et al., 2008).

Advocates of GWA studies argue that they overcome or mitigate many of the limitations of candidate gene studies. First, the large number of SNPs that are tested for association makes transparent the need to correct for multiple-hypothesis testing, which is achieved by imposing the genome-wide significance threshold of p < 5×10⁻⁸ (McCarthy et al., 2008). Moreover, GWA studies, as a practical matter, tend to be based on larger samples (as indeed they must be to have any hope of identifying a SNP that reaches genome-wide significance).

Second, Bayes’ Rule implies that conditional on observing an association at the genome-wide significance level, the association is likely to be true even if the study had only modest statistical power to detect the association in the first place; see Benjamin et al. (2012) for calculations.

Third, GWA data can be used to mitigate the potential confound of population stratification. In particular, it has become a common practice in GWASs to (a) estimate the first four principal components (PCs) of all the genotypes measured by the gene chip (the number four having emerged as a convention), (b) drop individuals who are genetic outliers as measured by these PCs, and then (c) include the PCs as control variables in the genetic association analysis. Intuitively, the PCs capture axes of correlation across the genome resulting from common ancestry. The PCs often have a geographic interpretation (Abdellaoui et al., 2013; Price et al., 2006, 2009). Controlling for PCs has become standard in GWA studies since Price et al. (2006) showed through simulation and empirical examples that doing so can eliminate spurious associations that are due to population structure. In Section S-5 of the Supplemental Material, we illustrate the effectiveness of PCs using a simple placebo test. Specifically, we show that controlling for PCs eliminates a spurious association between educational attainment and a SNP for lactose intolerance that is known to vary in frequency across individuals with different ancestries (Bersaglieri et al., 2004; Campbell et al., 2005). (In contrast, the most common way of addressing population stratification in candidate-gene studies, namely including controls for self-identified race, does not eliminate the spurious association.)

There are thus many reasons to expect findings from GWA studies to replicate more consistently than findings from candidate gene studies. And experiences from the literature on complex anthropometric and medical traits suggest that GWA findings do in fact have a vastly superior replication record (Visscher et al., 2012). But do positive GWA findings from studies of complex behavioral traits similarly identify credible genetic associations that replicate consistently? And if the findings do replicate consistently, do they replicate consistently because what is being observed is a real genetic signal, or could it be that population stratification generates a spurious association in both the discovery sample and the replication sample? If GWA studies do identify credible and replicable genetic associations, then they are a promising response to the non-replicability problem in gene-discovery research in the social sciences.

Until recently, virtually all GWA studies with positive findings have been studies of anthropometric or medical traits. For this reason, it may be inappropriate to infer from the superior replication record of GWA studies of medical traits that positive findings from GWA studies of behavioral traits are going to replicate consistently. If true genetic associations with behavioral traits have smaller effect sizes than true associations with anthropometric and medical traits, then GWA studies on behavioral traits will tend to generate less reliable results because they have lower power to detect true associations. Furthermore, while the convention of controlling for four PCs may be sufficient to minimize population-stratification concerns for anthropometric and medical traits, it might not be sufficient for behavioral traits, which may be characterized by more subtle population stratification.

While earlier GWA studies of behavioral traits (Benyamin et al., 2014; de Moor et al., 2012) have largely come up empty-handed (probably due to lack of power), a recent GWAS on educational attainment with a combined sample of over 100,000 individuals (Rietveld et al., 2013) identified three SNPs that meet the standard criteria for establishing a GWAS association, (i) and (ii) listed above. The effect sizes of the associations identified by Rietveld et al. are indeed small: the largest effect size corresponds to an R² of only approximately 0.02% (equivalent to about one month of schooling per allele). This is far smaller than the effect sizes for medical and anthropometric traits, for example, it is less than one tenth the R² of the largest associations discovered for height (R² = 0.4%; Lango Allen et al., 2010) and BMI (R² = 0.3%; Speliotes et al., 2010). The Rietveld et al. results therefore can serve as a test case for the robustness of the GWA approach to behavioral traits.

We sought to investigate (a) whether the Rietveld et al. results replicate in an independent sample with far more stringent controls for population stratification than are typically applied in GWA studies of medical and anthropometric traits, and (b) whether there is any evidence overall that the meta-analytic results are contaminated by unaccounted-for population stratification.

Study 1 – Replication of Specific SNPs in 23andMe with Extensive Controls for Stratification

Method

Study 1 sought to replicate the three genome-wide significant SNPs identified by Rietveld et al. in a new independent sample. The Rietveld et al. study tested approximately J = two million SNPs for association with educational attainment by running the following regression separately for each SNP j ε {1, 2, …, J}:

$$y_i={\mu }_j+{\beta }_j{x}_{ij}+{\gamma }_j{\mathit{Z}}_i+{\epsilon }_{ij},$$ (1)

where y_i is the dependent variable (the phenotype); μ_j is a constant term; x_ij is the number of reference alleles (0, 1, or 2) individual i is endowed with at SNP j; β_j is the coefficient of interest; and Z_i is a vector of controls, which include age, sex, and the first four PCs of the variance-covariance matrix of the genotypic data. Rietveld et al. studied two dependent variables: EduYears, a measure of the number of years of schooling completed by the individual, and College, a binary variable equal to one if the individual had completed a college degree or its equivalent. (The point biserial correlation between the two measures is roughly 0.8; see Supplemental Materials S-1.) The tests of association with EduYears were conducted by running the linear regressions described above, and the tests of association with College were conducted analogously using logistic regressions.

We sought to replicate the original associations using data provided by 23andMe, a cohort based on a sample of volunteer participants (Eriksson et al., 2010) that was not included in the Rietveld et al. study. After applying quality-control filters and restricting to individuals of European descent who responded to a survey question about educational attainment, the sample size is N = 34,428. Because of the small effects, replication samples of this magnitude are required for adequate power. Given the sample size of 34,428, our power to replicate an association with R² = 0.02% at p < 0.05 is 75% (see Supplemental Materials S-6).

We used the same regression models (1) as in Rietveld et al., except that in our analysis, the vector of controls Z_i includes (in addition to age and sex) the first 25 PCs from the sample genotype covariance matrix—compared to only 4 PCs in Rietveld et al.—in order to reduce potential population-stratification confounding by partialing out more of the population structure.

Results

As shown in Table 1, all three SNP associations reported in Rietveld et al. replicate at a nominal significance level of 0.05, in the same direction and with similar effect sizes as in the original report. The replication of effect sizes suggests that the additional controls for population stratification from including more than 4 PCs made little difference (for related evidence, see also Supplemental Material S-5). As a caveat, we note that since all research participants are completely anonymous to us, we cannot rule out overlap between the 23andMe sample and the Rietveld et al. discovery or replication sample, in which case the new results would not be fully independent from the Rietveld et al. results. We believe, however, that such potential overlap is likely to be miniscule and is therefore unlikely to drive our replication findings.

Table 1.

Replication in 23andMe Data

College	23andMe			Rietveld et al. Discovery			Rietveld et al. Replication
	OR	S.E.	p-value	OR	S.E.	p-value	OR	S.E.	p-value
rs12206087	1.035	0.018	0.046	1.049	0.011	1.06×10−5	1.042	0.021	0.022
rs11584700	0.954	0.020	0.025	0.924	0.012	2.07×10−9	0.923	0.022	4.86×10−4
rs4851266	1.071	0.019	0.0001	1.069	0.012	2.20×10−9	1.058	0.022	0.003
N		34,428		95,407–95,419			23,663–23,668
EduYears	23andMe			Rietveld et al. Discovery			Rietveld et al. Replication
	Beta	S.E.	p-value	Beta	S.E.	p-value	Beta	S.E.	p-value
rs12206087	0.058	0.020	0.004	0.106	0.018	4.19×10−9	0.077	0.034	0.012
rs11584700	−0.053	0.025	0.032	−0.086	0.021	2.98×10−5	−0.126	0.041	9.61×10−4
rs4851266	0.086	0.021	4.28×10−5	0.076	0.018	3.64×10−5	0.103	0.035	0.002
N		34,428		101,048–101,061			23,523–23,573

Notes: Beta is the effect of an increase in one reference allele on years of schooling estimated by the linear regression model (1) for EduYears, and OR is the odds ratio (the relative likelihood of attending college for an individual with one more reference allele) estimated by the analogous logistic regression for College. The Rietveld et al. sample sizes are given by a range because different sample sizes are available for the three SNPs. In Rietveld et al., rs9320913 is significantly associated with EduYears and rs11584700 and rs4851266 with College. Because rs9320913 is unavailable in the 23andMe data, we use rs12206087 as a (very reliable) proxy for rs9320913 (R² = 0.99; see Supplemental Materials S-2.3); the “rs12206087” results for Rietveld et al. are actually the results for rs9320913. The bold rows in the College panel indicate the SNPs found by Rietveld et al. to be associated with College in their discovery sample; analogously for the EduYears panel.

Study 2 – Robustness of Polygenic Scores in STR and QIMR with Two Distinct Methods of Controlling for Stratification

Method

While Study 1 used a new dataset to replicate the three genome-wide significant SNPs reported by Rietveld et al., Study 2 used some of the same data as in the original report to probe the robustness of Rietveld et al.’s reported “polygenic score” results to potential confounding from population stratification. Following Purcell et al. (2009), polygenic scores are commonly constructed in the GWA literature in order to allow investigators to evaluate the joint predictive power of a large number of SNPs (possibly including SNPs whose effects are too small or estimated too imprecisely to reach genome-wide significance).

Following a common approach in the genetics literature (Purcell et al., 2009; Yang et al., 2012), Rietveld et al. constructed a polygenic score (ĝ_i) for each individual i as equal to a weighted sum of the number of reference alleles (0, 1, or 2) across a set of SNPs, where the weights are derived from the regression coefficients from a GWAS of either EduYears or College. They then evaluated the predictive power of an individual’s score ĝ_i for the individual’s educational attainment using two hold-out samples (i.e., samples excluded from the GWAS used for estimating the weights): the Swedish Twin Registry (STR) sample and the Queensland Institute of Medical Research (QIMR) sample. Although the original datasets are family-based samples, one member from each family was selected at random to be included in the analyses. In each sample (and for scores constructed using GWASs of each of EduYears and College), Rietveld et al. tested four scores constructed from increasingly large sets of SNPs, the sets of SNPs whose GWAS associations with educational attainment fell below the respective p-value thresholds: 5×10⁻⁸ (i.e., only the genome-wide significant SNPs), 5×10⁻⁵, 5×10⁻³, and 1 (i.e., all SNPs). For each polygenic score ĝ_i, Rietveld et al. examined its predictive power by running the regression:

$${\mathit{\text{EduYears}}}_i=\mu +\beta {ĝ}_i+\gamma {\mathit{Z}}_i+{\epsilon }_i,$$ (2)

where the dependent variable is always EduYears (never College), μ is a constant term; β is the coefficient of interest; and Z_i is a vector of controls, which include age, sex, and age×sex, but no PCs (though PCs were included as controls in the GWA analyses that generated the weights for constructing the ĝ_i’s). Rietveld et al. found that the incremental predictive power of the score (i.e., the increase in R² from estimating regression (2) with the score as an independent variable relative to the R² without the score) was larger when more SNPs were included in the score. The score containing all SNPs, which had the largest incremental predictive power, accounted for approximately 2% of the variance across individuals in educational attainment.

To explore the robustness of original prediction findings, we re-ran these prediction analyses using two distinct methods that control more stringently for population stratification. In the first, we estimated the same regression model (2), except that we additionally included in the vector of controls the first 20 PCs as control variables. In the second, we estimated mixed linear models (Kang et al., 2010) in place of the regression models. Conceptually, these models involve two steps: (i) the genome-wide data are used to estimate the degree of genetic similarity between each pair of individuals in the sample, and (ii) unlike in standard regression where the covariance of the error term (in an educational-attainment regression) between any two individuals is assumed to be zero, the covariance is fitted as an increasing linear function of the individuals’ genetic similarity. In other words, to the extent that two individuals are more recently descended from a common ancestor (as very accurately measured by overall genetic similarity)—and thus are more likely be similar on unobserved environmental factors—these individuals are treated as correlated observations on the relationship between educational attainment and the score.

Results

The results are shown in Table 2. The upper panel shows the results from the association analyses with the scores constructed using different p-value thresholds. We separately report results from the STR and QIMR samples and separately for scores constructed from weights estimated using College and EduYears. The middle and lower panels show results, respectively, from regressions with 20 PCs included as controls and from mixed linear models. Each coefficient is the estimated effect of a one-standard-deviation increase in the score.

Table 2.

Results from Additional Analyses of Polygenic Scores in QIMR and STR Data

			Queensland Institute of Medical Research (QIMR)				Swedish Twin Registry (STR)
Threshold for inclusion of SNPs in PGS			< 5×10−8	< 5×10−5	< 5×10−3	All SNPs	< 5×10−8	< 5×10−5	< 5×10−3	All SNPs
No PC Adjustment	College	Beta	0.0495	0.1502	0.3581	0.5630	0.1706	0.1984	0.3469	0.5506
		S.E.	0.0554	0.0554	0.0551	0.0545	0.0496	0.0496	0.0496	0.0492
		p-value	0.3702	0.0067	9.1×10−11	1.4×10−24	6.1×10−4	6.9×10−5	3.1×10−12	1.2×10−28
		ΔR2	0.0002	0.0021	0.0118	0.0291	0.0017	0.0023	0.0072	0.0180
	EduYears	Beta	−0.0221	0.2478	0.3326	0.5544	0.1353	0.2481	0.3194	0.5617
		S.E.	0.0554	0.0551	0.0551	0.0548	0.0496	0.0496	0.0496	0.0492
		p-value	0.6894	7.6×10−6	1.7×10−9	7.1×10−24	6.5×10−3	6.4×10−7	1.3×10−10	1.0×10−29
		ΔR2	0.0000	0.0056	0.0102	0.0282	0.0011	0.0037	0.0061	0.0188
Controlling for 20 PCs	College	Beta	0.0502	0.1617	0.3567	0.5508	0.1640	0.1968	0.3407	0.5445
		S.E.	0.0554	0.0554	0.0551	0.0548	0.0496	0.0496	0.0496	0.0492
		p-value	0.3671	3.5×10−3	1.1×10−10	1.5×10−23	9.9×10−3	7.8×10−5	7.3×10−12	4.9×10−28
		ΔR2	0.0002	0.0024	0.0117	0.0278	0.0016	0.0023	0.0069	0.0176
	EduYears	Beta	−0.0043	0.2604	0.3122	0.5372	0.1410	0.2423	0.3059	0.5588
		S.E.	0.0554	0.0554	0.0551	0.0548	0.0496	0.0496	0.0496	0.0492
		p-value	0.9400	2.6×10−6	1.7×10−8	1.8×10−22	4.6×10−3	1.1×10−6	7.8×10−10	2.0×10−29
		ΔR2	0.0000	0.0062	0.0090	0.0265	0.0012	0.0035	0.0056	0.0186
Mixed Linear Model Analysis	College	Beta	0.0538	0.1505	0.3383	0.4920	0.1697	0.1902	0.3387	0.5601
		S.E.	0.0571	0.0581	0.0574	0.0581	0.0504	0.0500	0.0500	0.0508
		p-value	0.3479	0.0096	3.8×10−9	2.5×10−17	7.5×10−4	1.4×10−4	1.1×10−11	2.4×10−28
		ΔR2	0.0003	0.0021	0.0105	0.0222	0.0017	0.0022	0.0068	0.0187
	EduYears	Beta	−0.0083	0.2303	0.2666	0.4947	0.1410	0.2403	0.3104	0.5662
		S.E.	0.0581	0.0584	0.0561	0.0587	0.0513	0.0504	0.0500	0.0504
		p-value	0.8863	7.9×10−5	1.9×10−6	3.7×10−17	6.0×10−3	1.9×10−6	5.1×10−10	2.4×10−29
		ΔR2	0.0000	0.0049	0.0065	0.0225	0.0012	0.0034	0.0057	0.0191
		N	3,544				6,770

Notes: Beta is the effect of a one-standard-deviation increase in the polygenic score on years of schooling estimated by the linear regression model (2) (the first two panel rows) or by the mixed linear model analysis (the last panel row); if Beta is positive, the score predicts EduYears in the same direction in the replication sample as in the discovery sample. S.E. is the estimated standard error of Beta, and the p-value is for a two-sided test. ΔR² is the increase in R² (in units of percentage points) from estimating a model that includes the polygenic score as an independent variable relative to estimating a model that excludes it.

When all SNPs are used to construct the score, it has the predicted sign in all analyses and accounts for approximately 2% of the variance in educational attainment. In STR (the larger and therefore better-powered cohort), the polygenic score is statistically significant in all scenarios, even when only genome-wide significant SNPs are included. The joint effect of the SNPs with p < 5×10⁻⁸ is approximately 0.1%–0.2% of variance in EduYears in STR. Since this polygenic score includes 3 SNPs (when constructed using College) or 5 SNPs (when constructed using EduYears), the results are roughly consistent with Rietveld et al.’s estimate that each of the most strongly associated SNPs explains approximately 0.02% of variance in EduYears. Overall, there is no systematic tendency for the predictive power of the scores to change when additional controls for stratification are included.

Study 3 – Replication and Within-Family Robustness of Polygenic Scores in FHS

Method

The gold standard for ruling out concerns about population stratification is to show that the association holds within families. The original Rietveld et al. study reported within-family analysis using the pooled STR and QIMR sample. For this within-family analysis, the linear polygenic score constructed using all SNPs in the GWAS of EduYears is strongly associated with educational attainment, and the score constructed using a p-value threshold of 5×10⁻³ is marginally significant. Power was too low to draw conclusions about the scores constructed using p-value thresholds of 5×10⁻⁵ and 5×10⁻⁸ (which contain information from fewer SNPs). The STR and QIMR analyses were based on sample sizes of 2,774 DZ twin pairs and 572 full sibling pairs, respectively.

In Study 3, we use data from an independent sample, the Framingham Heart Study (FHS), to attempt to replicate the within-family analyses of the linear polygenic scores. FHS is an epidemiological study on three generations of individuals in the Massachusetts town of Framingham that was not included in any of Rietveld et al.’s analyses (see Supplemental Material S-4). In this sample, there are 395 families with two or more full biological siblings. Fewer SNPs are available in FHS than in STR and QIMR (see Supplemental Material S-4.1). Consequently, the polygenic scores in Study 3 are expected to have lower explanatory power than the analogous scores from Study 2. Our focus here is on examining, within the FHS dataset, how the estimated effect of the score is affected by restricting the analysis to within-family variation.

Our analyses proceeded in three steps. First, we applied quality controls to the data, pruned the SNPs for linkage disequilibrium, and then constructed the polygenic score using the meta-analytic results from Rietveld et al. Second, we identified all biological full siblings. Finally, we tested the score (ĝ_i) within-family by running regressions of the following form:

$${\mathit{\text{EduYears}}}_i=\beta {ĝ}_i+{\sum }_{k=1}^K{\gamma }_k{X}_{ik}+{\epsilon }_i,$$ (3)

where i indexes individuals, k indexes families, and X_ik is an indicator variable that takes the value 1 if individual i belongs to family k and 0 otherwise. Including the “family fixed-effect” X_ik is equivalent (except for the resulting R²) to running a regression after both EduYears_i and the score ĝ_i are demeaned at the family level; hence the analysis uses only the within-family variation in EduYears and the within-family variation in the score. To account for the non-independence of the error term among siblings, we cluster the standard errors (Liang & Zeger, 1986) at the level of the family. Since we expected to have less power for this analysis than Rietveld et al. due to the smaller number of individuals and the smaller number of SNPs, we only ran these analyses for two scores, one constructed from all SNPs in the sample and one using a p-value threshold of 5×10⁻³. (We did not conduct within-family tests of the individual SNPs because our statistical power would be less than 7%—too low to draw a meaningful conclusion regardless of how the analysis turns out; see Supplemental Material S-6.)

Results

Each coefficient in Table 3 is the estimated effect of a one-standard-deviation increase in the score. Columns 1 and 2 report the results from the new within-family analyses using the FHS data: whether or not we control for 20 PCs, both polygenic scores constructed from all SNPs and from SNPs reaching p < 5×10⁻³ are positively and significantly associated with educational attainment. In columns 3 and 4 we also report analyses analogous to those from Study 2 (i.e., excluding the family fixed effects, thus leveraging both between- and within-family variation in the score). In these analyses, both scores are positively associated with educational attainment, again with similar results with and without the PC controls. The score from SNPs reaching p < 5×10⁻³ is marginally significant, and the score from all SNPs is highly statistically significant.

Table 3.

Results from Analyses of Polygenic Scores for EduYears in FHS

		Within-Family Variation Only		Between- and Within- Family Variation
		(1)	(2)	(3)	(4)
Threshold for inclusion of SNPs in PGS		< 5×10−3	All SNPs	< 5×10−3	All SNPs
No PC Adjustment	Beta	0.2386	0.2677	0.1142	0.2448
	S.E.	0.0934	0.1034	0.0637	0.0614
	p-value	0.011	0.010	0.073	7.44×10−5
	ΔR2	0.0036	0.0037	0.0031	0.0141
Controlling for 20 PCs	Beta	0.2308	0.2642	0.1173	0.2534
	S.E.	0.0947	0.1044	0.0634	0.0621
	p-value	0.015	0.012	0.065	5.13×10−5
	ΔR2	0.0033	0.0036	0.0031	0.0140
N, #individuals		1,256		1,256
N, #families with ≥ 2 children		395		395

Notes: Beta is the effect of a one-standard-deviation increase in the polygenic score on years of schooling estimated by the linear regression model (3) (columns 1 and 2) or by linear regression model (2) (columns 3 and 4); if Beta is positive, the score predicts EduYears in the same direction in the replication sample as in the discovery sample. S.E. is the estimated standard error of Beta, and the p-value is for a two-sided test. ΔR² is the increase in R² (in units of percentage points) from estimating a model that includes the polygenic score as an independent variable relative to estimating a model that excludes it.

Summary

To summarize, in Study 1 we replicate in an independent sample the associations between educational attainment and Rietveld et al.’s (2013) three genome-wide significant SNPs, using more stringent controls for population stratification than is typical in the GWA literature; the next two studies show that polygenic scores robustly replicate in regressions with controls for population stratification and in within-family analyses.

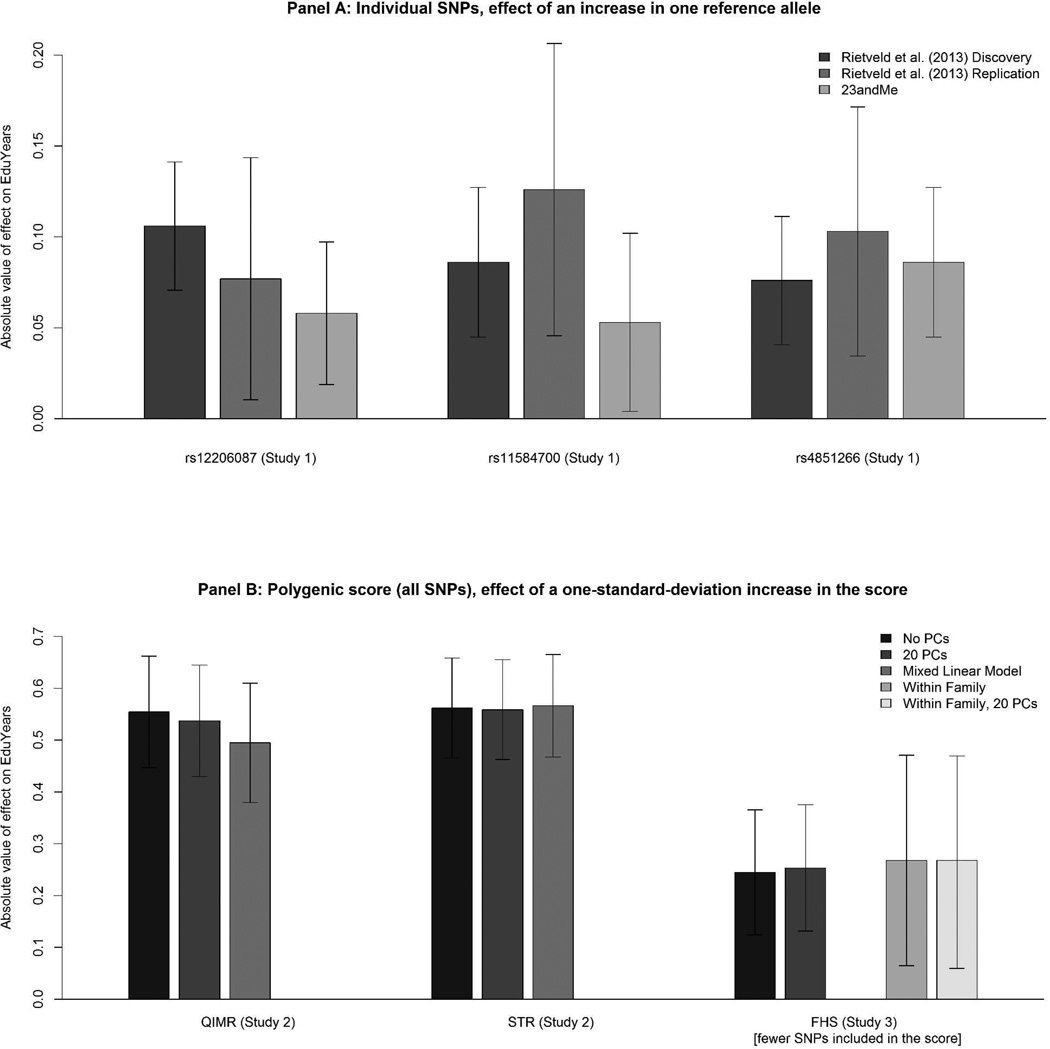
To facilitate comparing the effect sizes across Studies 1–3 and Rietveld et al.’s analyses, Figure 1 shows 95% confidence intervals for the effect on EduYears. An effect size of 0.1, for example, is approximately 1 month of schooling. For the individual SNPs, the effects are per reference allele, and for the polygenic score containing all SNPs, the effects are per one-standard-deviation increase in the score. Panel A shows that the effect sizes of the genome-wide significant SNPs are comparable across datasets. The effect sizes of the polygenic scores in Panel B are also similar in QIMR and STR across the two different datasets and methods to control for population stratification. The effect sizes of the polygenic score in FHS (Study 3) are not comparable to those from QIMR and STR; the effect sizes are attenuated in FHS because the scores are constructed from the smaller number of SNPs available in this sample (see Supplemental Material S-4). Within FHS, the effect sizes remain similar across different methods to control for population stratification, including the within-family analyses.

Figure 1.

Comparison of effect sizes across studies

Notes: Panel A shows the (absolute value of the) effect on years of schooling of a change in one reference allele for each of the three individual SNPs, with 95% confidence intervals. The results are a visual representation of the numbers in Table 1. Panel B shows the (absolute value of the) effect on years of schooling of a change in one standard deviation of the polygenic score that includes all SNPs, with 95% confidence intervals. The results for QIMR and STR are a visual representation of the numbers in the “all SNPs” columns of Tables 2. Similarly for the results for FHS and the “all SNPs” column of Table 3 (but note that the score in FHS is not comparable with the other two scores, since it is based on fewer SNPs).

While these results are encouraging, we also note a potential limitation of this study. Our evidence, especially the finding that the score is significantly associated with educational attainment in within-family analyses, suggests that it is extremely unlikely that the findings of Rietveld et al. are largely an artifact of stratification. However, biases due to very subtle population stratification may still account for some of the observed relationships between educational attainment and some of the individual SNPs. This possibility cannot be conclusively ruled out until large enough family samples (e.g., N = 47,000 sibling pairs, see Supplemental Material S-6) are available to enable adequately powered within-family tests of association with individual SNPs. This potential limitation applies to all GWA studies. Our findings suggest, however, that the individual SNP associations with educational attainment are robust even when we include substantially more stringent controls than is standard in medical genetics.

Discussion

The contrast between the robustness of our findings and the disappointing replication record of most candidate gene studies of behavioral traits is striking. To draw the appropriate methodological conclusions, it is necessary to understand the causes of this difference.

A first major contributing factor is that the Rietveld et al. analyses were based on a sample size that was unprecedentedly large by the standards of social-science genetics. If, as now seems likely, the effects of individual genetic variants on most behavioral traits are small, much larger samples than are generally used are required to produce credible findings. This is a methodological lesson that applies to all studies whether they be GWA studies or not. However, as an empirical matter, candidate gene studies tend to be based on much smaller samples. Though it seems clear that much larger samples are needed, it is important to recognize that statistical power also depends on the reliability of the available phenotypic measure. Researchers will sometimes face a tradeoff between studying a studying a cruder variable available in a large sample (e.g., educational attainment) or more proximal variables available in a smaller sample (e.g., cognitive ability). Rietveld et al. (2013, SOM Section 7) provide a framework for quantifying this tradeoff.

A second contributing factor is that some of the discipline that comes from the hypothesis-based research of existing candidate gene studies is illusory: because a vast majority of genes are expressed in the brain (Ramsköld, Wang, Burge, & Sandberg, 2009), it is usually possible to create an ex post rationalization for an observed association between a candidate gene and a behavioral trait that sounds at least superficially biologically plausible. Thus, the main advantage of the candidate gene approach—namely the theoretical discipline that it imposes on the investigator—may be exaggerated.

We believe there are two key implications of our findings for research on genetics of behavioral traits. First, our results suggest that standard GWAS protocols from epidemiological research can indeed be successfully applied to the study of behavioral traits and may therefore offer a way to avoid the replication failures that are plaguing much research on the genetics of complex behavior. Second, even if (given the current state of biological knowledge) current candidate-gene approaches are not bearing fruit, this does not rule out an eventual “comeback” for hypothesis-based research in the genetics of behavioral traits. In fact, we envision that as the number of credibly established associations from GWA studies rises, these discoveries will usher in a new era of “empirical candidate gene” studies in which the candidates are drawn from among the SNPs identified by GWA studies of related phenotypes. For example, the SNPs associated with educational attainment could be used as candidates to study cognitive and personality traits that may be part of the causal pathway. Such follow-up studies will of course need to be adequately powered to produce robust results, but since the GWAS results restrict the number of SNPs that are subsequently tested for association, the p-value threshold can be set much more liberally than the level of genome-wide significance.

What does the finding of small effect sizes—reported by Rietveld et al. and replicated here—imply about how genetic research in psychology should be conducted and what its payoffs will be for the field? An immediate implication is that current research using genotypic data in laboratory experiments is almost certainly underpowered, and therefore psychology should accelerate its move away from such methods, as they are unlikely to yield robust findings. A more subtle implication of the small effect sizes is that—as Turkheimer (2012) has persuasively argued—exuberant forecasts that the availability of genetic data will quickly transform the social sciences should be viewed skeptically. In principle, a genetic variant identified in an association study can explain a tiny part of the variation in the phenotype and yet point to an interesting biological system (and this has happened several times in medical genetics). In practice, it seems likely that SNPs with smaller effect sizes, on average, are more likely to operate on the phenotype through distal causal pathways involving a large number and many layers of mediating environmental factors. Therefore, it is conceivable that the identification of SNPs with very small effects will not lead to a useful psychological theory of the phenotype.

At present, it remains an open question to what extent the identification of individual SNPs will reveal new biological and psychological insights for highly polygenic behavioral traits. But we believe it is likely that genetic-association research will benefit psychology in the long run for at least two other reasons. First, even if genetic associations can only be discovered in samples of many tens of thousands of individuals, once the genetic variants to focus on have been identified, large-but-attainable samples of a few thousand individuals will provide sufficient statistical power to address interesting research questions, such as the nature and magnitude of gene-environment interactions.

Second, even though individual genetic variants have very small effects, polygenic scores can have large enough effects to be usable even in relatively small samples. The polygenic score explored here has modest explanatory power (R² ≈ 2%), but when the weights for constructing the score are estimated in larger samples, the explanatory power will be much greater. For example, Rietveld et al. (Table S26 in SOM) estimate that a polygenic score constructed using results from a discovery sample with N = 500,000 will have R² ≈ 12%. We anticipate that such sample sizes will be attainable in the next few years, making it possible to construct such a score. Once a polygenic score with R² = 12% can be calculated for each genotyped participant in a study, a sample of only 62 participants will be needed for 80% power to detect its effect.

In summary, our results suggest that in psychology, a shift away from candidate gene studies and toward GWA studies is likely to be fruitful. However, before the potential payoffs can be realized, the focus of much research on the genetics of behavioral traits will need to be reoriented, and new research infrastructures will need to be created—for example, to build much larger sample sizes than most GWA studies of behavioral traits have had access to. Nevertheless, we believe that this investment is worth making because it may lead to accumulation of reliable and replicable knowledge about the genetics of behavioral traits.