Figure 1.

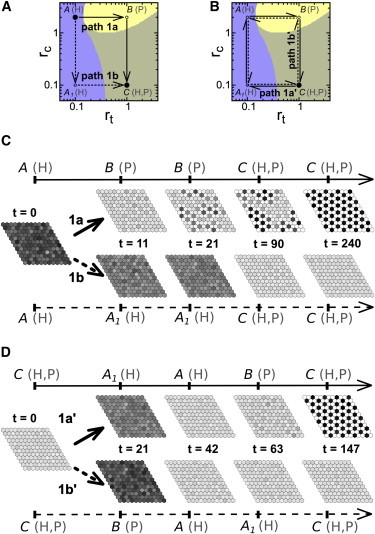
Pattern selection achieved through a specific global path. (A and B) Paths (arrows) across the parameter space of trans r_t and cis r_c interaction strengths. (Solid circles) Initial and final points of the paths; (open circles) intermediate vertex points. The temporal evolution of the paths is shown in Fig. S4. It is indicated within parentheses at relevant points of the path (denoted by letters A, B, A₁, and C) whether the homogeneous (H) and/or the salt-and-pepper (P) patterns are stable. The paths cross different domains (colors) each defined by which of these patterns are stable: H (blue), P (yellow), or H and P (gray). These domains have been plotted using data for deterministic dynamics with periodic boundary conditions in Formosa-Jordan and Ibañes (22). Stability of these patterns for stochastic dynamics is found in Fig. S5. (A) Paths 1a (continuous line) and 1b (dashed line) start at point A and end at point C. (B) Paths 1a′ and 1b′ start and finish at the same point C. Path 1a′ (continuous line) is clockwise whereas path 1b′ (dashed line) is counterclockwise. (C and D) Snapshots of the tissue state over time (t) when the same signal acts in all cells of the tissue at the same time (Scenario 1) and changes the values of the parameters (C) permanently according to paths 1a or 1b, or (D) transiently according to paths 1a′ and 1b′. The system initially (t = 0) exhibits the H-pattern. The parameter space points, and whether the H- or P-patterns are stable for these parameter values, are indicated at each depicted time. Additional parameter values are τ = 10, t_up = 11, t_prop = 0, b = 1000, n = 2, V = 1000, and those detailed in Table S1 and Materials and Methods. To see this figure in color, go online.