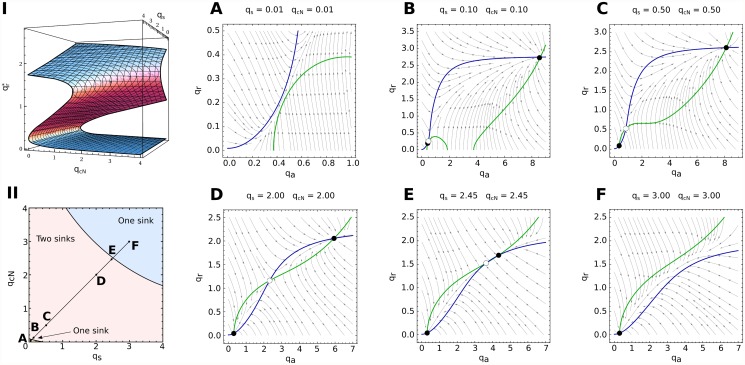
Fig 4. Adiabatic elimination of the fast variables q r and q a.
Due to the fast dynamics that HetR and NtcA exhibit, we can approach the treatment of the system by adopting a point of view that follows the slower variables q s and q n. From this viewpoint, the time-evolution of the pair (q s(t), q n(t)) is considered by assuming that q r and q a instantaneously relax to an equilibrium, which corresponds to a sink (, ) for the fixed pair (q s(t), q n(t)). Depending on the region of the (q s, q n)-plane, there are three fixed points (two sinks corresponding to the highest and the lowest concentrations respectively and a saddle in the middle) or one (a sink) for q r and q a (I and II). There are two one-sink regions that are separated from the two-sink region by saddle-node bifurcations (A-F). Sinks and saddles are represented by filled and unfilled circles respectively and arrows indicate the flow of the dynamics. We can then imagine the dynamics of q s and q n as evolving either in the bottom or in the top branch of I. In the two-sink region, both branches are plausible and the history of the dynamics determine the solution (hysteresis effect): a dynamics in a branch will continue in it until experiencing a bifurcation in the (q r, q a) plane (see Fig. 5 for examples).