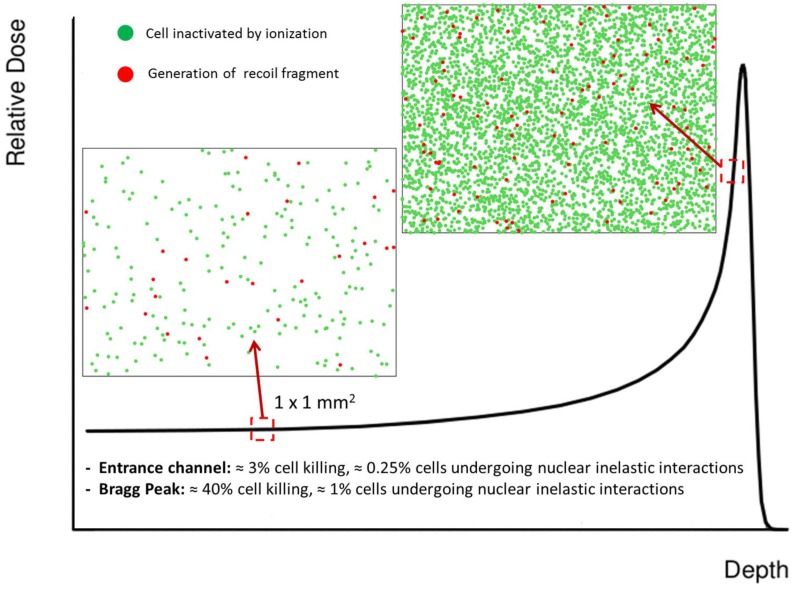
Figure 5.
The figure schematically shows the impact of ionization and target fragmentation in tissue sections of 1 × 1 mm2. The effect is considered at two different positions along the depth-dose profile. The LEM code was used to estimate cell survival probability [14,15]. The expected contribution of target fragments is calculated assuming that in water about 1% of primary protons undergo nuclear inelastic interactions per traversed cm. We chose a fluence of 2.5 × 108 p/cm2 for the primary beam, and assumed that cell nuclei cover an area of ≈100 μm2. This means that we can expect an average of 250 particles traversing a nucleus. When following protons traversing 1 mm of tissue (stack of 100 cells), we thus expect an average of 0.25 protons undergoing inelastic nuclear reactions. In other words, we will have one fragmentation event every fourth stack of cells, which translates to what is shown in the figure. Importantly, we only show cells where target fragments are generated, but a fraction of those fragments might have enough energy to traverse a few cell nuclei before coming to rest. This is true especially for light fragments (see also Table 1). Even though both the contributions of ionization and fragmentation increase when approaching the Bragg peak, at that position the biological effect is mainly due to ionization events. On the contrary, in the entrance channel the predicted survival is high, and therefore a significant role might be played by low-energy target fragments.