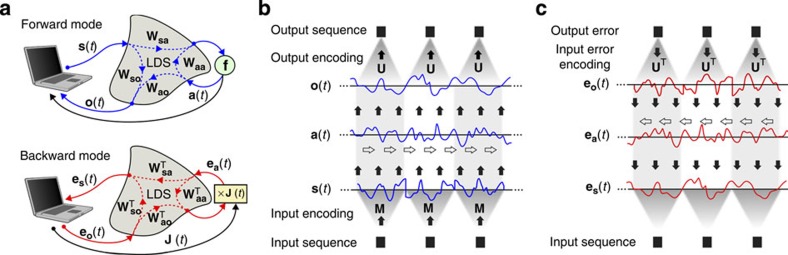
Figure 1. Schematic of physically implemented backpropagation.

(a) Illustration of the most general set-up of the physical neural network studied in this paper. The top diagram shows how the signals propagate through the system and the nonlinear feedback with blue arrows during the forward pass. The filter operations are depicted with dashed lines running through the LDS, which is depicted as a grey blob. The bottom diagram shows the error backpropagation phase, where the signal runs backwards through all functional dependencies. Here filter operations run in the opposite direction such that they are represented by the transpose of their impulse response matrices. Note that the computer is not in the loop during the forward or backward pass, but only serves to send out a predefined signal, and to record at the same time. (b) Depiction of the masking principle in the forward direction. At the bottom, we see three consecutive instances of an input time series. Each of these is converted into a finite time segment through the masking signals M(t). These segments are next concatenated in time and serve as the input signal s(t) for the dynamical system (where time runs according to the white arrows), and which in turn generates an output signal o(t). The output signal o(t) is divided into finite length pieces, which are decoded into output instances of an output time series using the output masks U(t). (c) The backpropagation process happens in a completely similar manner as in the forward direction. This time, the transpose of the output masks serve as the encoding masks. Finally, the input error signal e_s(t) is also segmented in time before it is used to determine the gradients w.r.t. M(t).