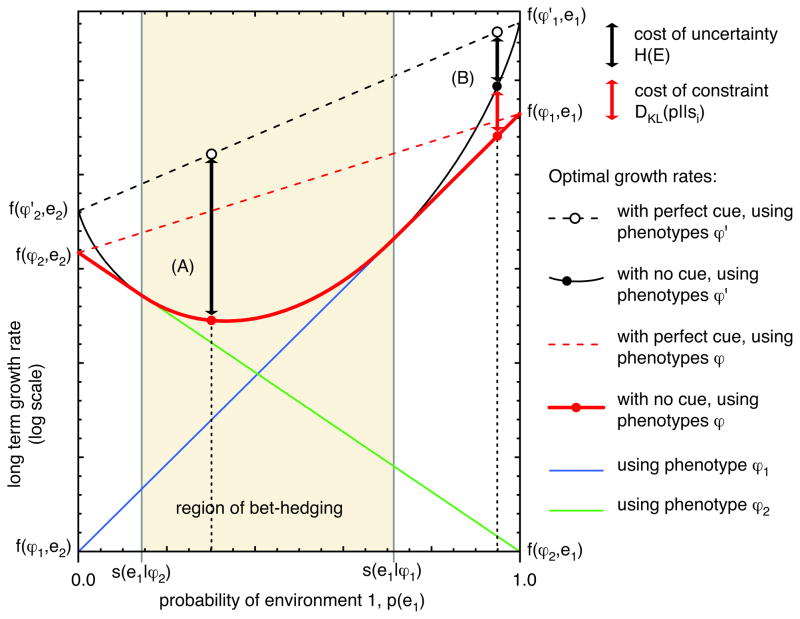
Figure 2.

Maximal growth rate when choosing the wrong phenotype is not fatal. The red solid line indicates the maximal growth rate using the two phenotypes ϕ₁ and ϕ₂. The black solid line is the growth rate that could be achieved with an unconstrained strategy, using the hypothetical phenotypes ${\varphi }_1^{\prime }$ and ${\varphi }_2^{\prime }$. Since the hypothetical phenotypes are fatal in the wrong environment, the optimal unconstrained strategy always uses proportional betting. In contrast, the optimal constrained strategy bet-hedges only in an intermediate range of environmental frequencies, labeled the “region of bet-hedging”. Outside that region, it uses the single phenotype that does best on average. (A) Within the region of bet-hedging, the constrained strategy does just as well as the unconstrained strategy. Compared to an unconstrained strategy that can perfectly predict the environment, both strategies incur a cost of uncertainty equal to the entropy of the environment H(E) (see Equations 8 and 15.) (B) Outside the region of bet-hedging, the constrained strategy does worse than the constrained strategy, since it cannot bet-hedge anymore. It always uses phenotype ϕ₁ on the right of the region, where environment e₁ is more common, and ϕ₂ on the left. The growth rate achieved is therefore exactly as with the decision-theoretic strategy, optimizing fitness in just one generation. In this case, the constrained strategy pays not only the cost of uncertainty, H(E), but also a cost of constraint that arises from the inability to bet strongly enough on the most common environment. This constraint further reduces the growth rate by the Kullback-Leibler divergence D_KL(p||s_i), which gets larger as we get farther from the boundary of the region of bet-hedging (see Equation 14.)