Figure 3.

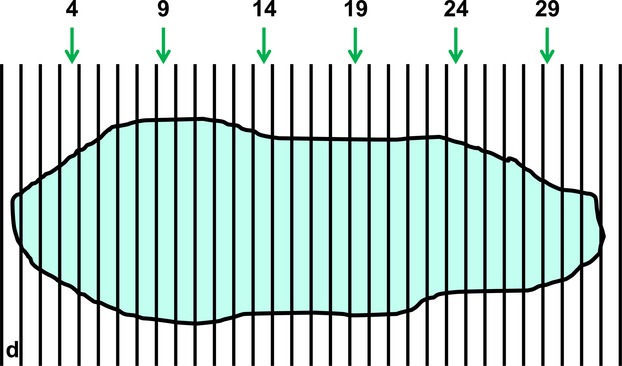
The principle of SUR sampling: sub-sampling from an exhaustive set of serial slices. In many forms of tomography, the whole specimen (or a part thereof) is reconstructed from an exhaustive set of serial slices through it. The slices might be obtained mechanically, optically or by medical imaging. Where 3D structural quantities are required from the specimen, it is much more efficient to make stereological estimates based on a SUR subset of these slices. Here, a specimen (e.g. an organ) has been serially cut into just 32 slices of thickness d with a random start position between 0 and d. Taking a SUR sample of every 5th slice with a random start between 1 and 5 (here, 4) yields slices 4, 9, 14, 19, 24 and 29. Using the right-facing section plane of each slice as the viewing plane, the resulting precision of estimation (for, say, specimen volume) is unlikely to overwhelm the natural variation between independent specimens belonging to the same study group. Indeed, the total observed variation (equal to the natural variation + estimation precision) depends more crucially on the number of specimens examined within a group.