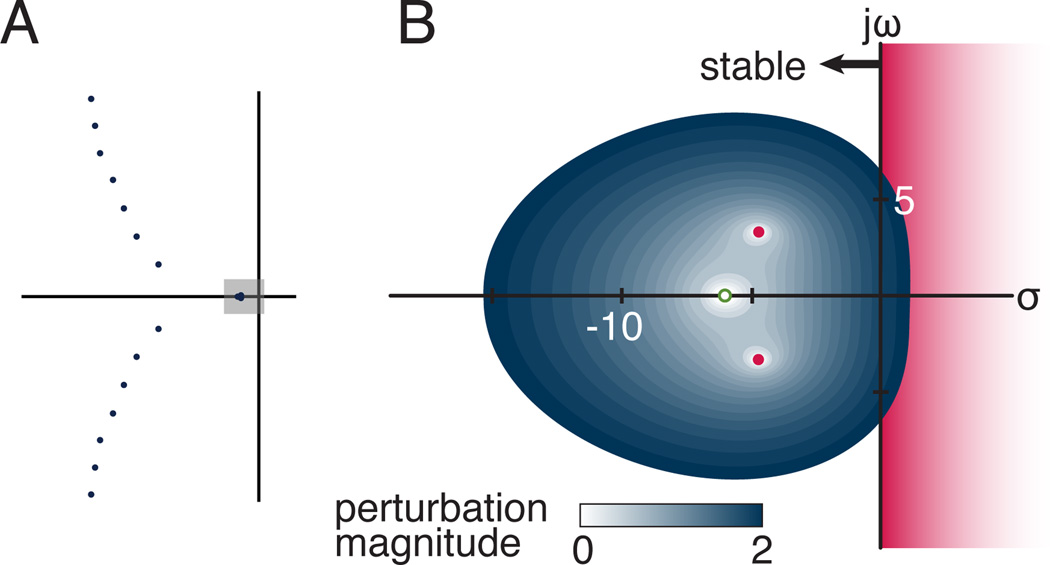
Figure 2.
Eigenvalues and pseudospectra for a single feedback gain pair at the nominal stance width. (A) A subset of the infinite number of eigenvalues for the delayed four-bar linkage model (S/W=2, kp=243 N-m/rad, and kv=57 N-m/rad/s). Shaded box is complex region surrounding the three dominant eigenvalues and enlarged in (B) The pseudospectra corresponding to a perturbation that caused the eigenvalues to go unstable is represented by dotted lines. The value of the smallest perturbation to cause any of the eigenvalues to go unstable was the stability radius for this system. For the neuromechanical system modeled here, the more negative eigenvalue (unfilled dot) went unstable at a lower level of perturbation than the dominant eigenvalues that were closer to the imaginary axis (filled dots).