MAGE: Matching Approximate Patterns in Richly-Attributed Graphs

Abstract

Given a large graph with millions of nodes and edges, say a social network where both its nodes and edges have multiple attributes (e.g., job titles, tie strengths), how to quickly find subgraphs of interest (e.g., a ring of businessmen with strong ties)? We present MAGE, a scalable, multicore subgraph matching approach that supports expressive queries over large, richly-attributed graphs. Our major contributions include: (1) MAGE supports graphs with both node and edge attributes (most existing approaches handle either one, but not both); (2) it supports expressive queries, allowing multiple attributes on an edge, wildcards as attribute values (i.e., match any permissible values), and attributes with continuous values; and (3) it is scalable, supporting graphs with several hundred million edges. We demonstrate MAGE's effectiveness and scalability via extensive experiments on large real and synthetic graphs, such as a Google+ social network with 460 million edges.

I. Introduction

Graphs are a convenient and ubiquitous means to represent many naturally occurring patterns. Rich with information, many graphs contain subgraph patterns that capture interesting dynamics among entities, but because of the size and complexity of these graphs, spotting such interesting patterns can be a difficult task. An analyst may want to analyze an intelligence network of various entities (e.g., people or events) connected with edges denoting gathered intelligence (as in Figure 1). The analyst will have some ideas about the structure of criminal behavior which drive the use of subgraph matching techniques to find potentially dangerous individuals.

Fig. 1.

An illustrative example of how MAGE finds patterns in an intelligence graph (left) with node and edge attributes. Node attributes: Person, Event, or Location. Edge attributes (amount of gathered intelligence for a pair of entities): Confirmed, Suspected, or Unlikely. A query (middle) looks for two indirectly related individuals, who were both confirmed at an event location and are believed to have attended the event (two lines connecting the corresponding nodes). The node with a star indicates a wildcard, which can take any attribute value. (All figures best viewed in color.) The rightmost figure shows an approximate match.

A Motivating Example

In Figure 1, the node attributes are the entity types, which can be a Person (orange circle), an Event (green square), or a Location (purple triangle), and the edge attributes are the confidence of intelligence for a pair of entities, which can be Confirmed (dotted line), Suspected (wavy line), and Unlikely (line with pluses). The graph labeled “Query ” shows a query that our analyst may issue, which looks for two indirectly related people, who appeared at the same location (thus, “confirmed” to be linked to a location), and were suspected of having attended an event together.

One challenge here is that the analyst might not know what values to assign to some of the nodes and edges in the query; so instead of guessing or assigning an arbitrary value, the analyst may want to assign a node or an edge with a wildcard attribute value, a feature that would allow the analyst to explore different hypotheses. However, it is not supported by many existing subgraph matching techniques.

The existing subgraph matching approaches that return only exact matches (if any) will not help the analyst solve complex tasks where attribute uncertainty is present. For the query in Figure 1, the system should be able to return a match filling in the wildcard, e.g., the person entity corresponding to node 3 in the result. Even with the wildcard, the exact specified structure may not exist in in the graph; under this scenario the system would return a “best-effort” match or approximation of the query. By generating both exact and near matches, we can provide the user with the top-k most closely matched subgraphs even if the initial query was not exactly present in the input graph.

Limitations of Existing Techniques

A representative set of early work on inexact pattern matching on graphs is G-Ray by Tong et al. [1], TALE by Tian and Patel [2], and SIGMA by Mongioví et al. [3]. More recently, Khan et al. proposed the NeMa approach [4], Fan et al. proposed a set of incremental pattern matching algorithms [5], [6] and the TopKDiv approach [7], and Cheng et al. proposed the kGPM framework [8]. The main limitations of these techniques are that they either (i) do not support edge attributes, (ii) need computationally-heavy indexes precomputed for the input graph, or (iii) return results that can significantly deviate from the query pattern, which may be difficult for users to comprehend.

Our Contributions

We present MAGE, short for Multi-Attribute Graph Engine, a pattern matching system for graphs with node and edge attributes that overcomes many of the challenges and limitations outlined above. It produces top-k closest subgraph matches for a variety of attributed input graphs. Our experimental evaluation shows that MAGE is a scalable tool that works for graphs from different domains, from intelligence applications to understanding the patterns of movie success. MAGE's major contributions include:

1. Support for node and edge attributes, expanding the effectiveness on real world data and increasing the types of questions that can be answered through graph querying.

2. Support for flexible queries with rich attributes, supporting queries with wildcards and multiple categorical attributes.

3. A fast & scalable multicore algorithm, handling real and synthetic graphs with hundreds of millions of edges, using random walk with restart (RWR) steady-state probabilities as proximity scores between nodes to determine how well a subgraph matches the query.

II. Problem Definition and Notation

Here, we formalize the subgraph matching problem that MAGE aims to solve. In its general form, we are given two graphs and and we wish to know if contains a subgraph that is equivalent to 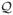. Table I describes the symbols used in the paper. This problem is often referred to as the subgraph isomorphism problem. Unfortunately, this problem is NP-Complete [9], making all general solutions computationally infeasible for even modest sized graphs. The problem we tackle is subtly different than the subgraph isomorphism problem and can be formally stated as follows:

Table I. Symbols and terminology used in this work.

Symbol	Description
	n × n adjacency matrix for
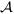
	n × t node-attribute matrix for graph
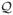
	Query subgraph to be extracted from
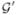
	(m + n) × (m + n) linegraph-modified bipartite graph
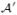
	Node-edge-attribute matrix for graph
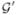
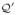
	Query subgraph after edge augmentation
M	A bijective mapping between edges of and edge-nodes in
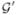
〈s, t〉	An edge leading from node s to node t
n	Number of nodes in
m	Number of edges in
t	Number of distinct categorical attributes
i,j & u,v	Indices of nodes 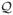in and in respectively.
λ	Ratio of approximated nodes and edges with correct attributes to the total number in a result

Given: (i) A graph whose nodes and edges have categorical attributes, (ii) a query graph 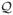showing the desirable configuration of nodes connected with edges, each assigned one or more attribute values (or a wildcard), and (iii) the number of desired matching subgraphs k.

Find: k matching subgraphs 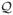_i (i = 1, …, k) that match query graph 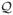as closely as possible, according to a goodness metric (which we cover in the Methodology section).

A. Preliminary: Querying on Node Attributes

Several approaches have been proposed to subgraph isomorphism problem. The work by Tong et al. proposes the G-Ray algorithm [1], which is a best-effort inexact subgraph matching approach that relies on RWR or personalized page rank values as the selection criterion when constructing query results. This approach carefully uses nodes as restarts when calculating the RWR values. We leverage this approach, but considerably modify it to allow multiple attributes as restarts in the RWR approximations (see Section IV-D). Approximate RWR is still a computationally expensive step that must be performed often. In Section IV-A, we show our approach to reducing query latency by decreasing RWR calculation times.

While G-Ray is an integral facet of MAGE, the limitations of the original algorithm are far too constrictive. The G-Ray algorithm is inadequate in supporting expressive querying as it does not support attributed edges, unknown query attributes, multiple attributes, and it incurs sizable query latencies on large graphs. We address these issues with MAGE. Using our linegraph augmentation approach, we support node and edge attributes with limited information by offering, wildcards and multiple attributes. To address the speed and scalability we utilize an approximate parallel RWR technique to quickly calculate the data needed to find good candidate matches.

III. Mage Overview

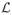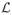In order to cover both edge and node attributes in we use an edge-augmentation method based on intuition from the linegraph transformation [10]. Under the canonical linegraph transformation, each vertex in the line graph of is an edge from . Two vertices in are connected if and only if their corresponding edges (from ) share a common endpoint in . Figure 2 demonstrates an example transformation with the key linegraph transformation occurring in (c).

Fig. 2.

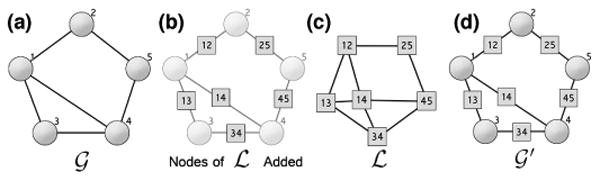
Linegraph transformation and edge augmentation used to support edge and node attributes in MAGE. (a) Input graph. (b) Intermediate step of linegraph transformation of , where a node for each original edge is created. (c) 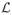( ) or 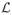is the linegraph of in which all edges from that shared a node in are now connected as nodes of 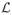. (d) Edge augmentation wherein we embed the edge-nodes of 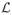( ) directly into to create .

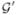By making use of the line-graph transformation on the starting graph , we can produce an attributed line graph 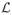where each of the edges in is represented by a node in 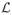. Rather than working with both 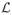and , we create 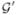which combines aspects of both and 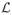. We insert a new edge-node on each edge of such that it is connected to the same vertices in 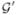that it connected to as an edge of . This process is illustrated with a toy graph in Figure 2d, where the edge-nodes are the square nodes splitting each edge of . Under this formulation, no two nodes in will be directly connected in 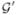. The same holds for all new edge-nodes in 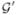. The newly created 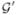is bipartite between the set of original nodes and the set of new edge-nodes; a fact we will use later in approach.

A. MAGE Subroutines

We divide the process of discovering matching subgraphs into several key steps: (i) finding the initial nodes to start our localized search, then (ii) finding nearby nodes that fulfill or approximate the desired attributes and (iii) approximating the structure of the edges interconnecting nodes from steps i and ii.

Detect-Candidate

The first node of each query approximation is located in the graph using Detect-Candidate in line 3 of Algorithm 3. This routine leverages attribute filtering, but primarily subgraph centerpieces suggested in [11]. Detect-Candidate selects the most central node of the query first to help narrow the scope of the candidate search.

Local-Search

Given a partially fulfilled set of query nodes, Local-Search (line 7 of Algorithm 3) will locate a node in 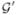corresponding to an unfulfilled node from 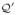. We generate heuristic scores (using RWR values) to pick the best candidate nodes. This approach will select nodes closer to the approximated query, keeping the selected nodes in the local area of the current approximated nodes.

Linker

The Linker, line 8 in Algorithm 3, approximates the query's edges in the dictionary graph. If the two selected nodes of the real graph are connected the edge is returned; otherwise, the shortest path is used as an approximation of the edge. This shortest path may introduce additional nodes in order to complete the pattern.

IV. Methodology

A. Random Walk with Restart (RWR)

MAGE uses proximity scores between nodes in data graph and query graph 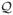to construct a subgraph 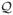_i approximating 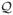. Specifically, the proximity between nodes i and j in a graph is the RWR value when node i is used as the restart point. The number of RWR values needed to find a matching subgraph is significant, because we use them to rank possible candidate nodes. Calculating RWR values is the most expensive step MAGE. Let F̂′ be our RWR values (see Equation 1). They are used to rank the goodness of nearby candidate nodes; unselected nodes that are near to the partially constructed query receiver higher RWR values and are therefore more likely to be chosen.

We have implemented a parallelized, sparse, power method that allows the fast calculation of RWR vectors. The canonical power-iteration method is a common approach to determine the RWR values (see Equation 1). Decompose row-wise into p submatrices each with m/p rows (call them ₁ … _p). Each _i is zero everywhere except its m/p rows such that they sum to , see Equation (2).

$${\hat{F}}_{k+1}=\alpha \mathcal{G}·{\hat{F}}_k+\hat{Y}$$ (1)

$${\hat{F}}_{k+1}=\alpha ({\mathcal{G}}_1+{\mathcal{G}}_2+\dots +{\mathcal{G}}_p)·{\hat{F}}_k+\hat{Y}$$ (2)

$${\hat{F}}_{k+1}=\alpha {\mathcal{G}}_1·\hat{F}+\alpha {\mathcal{G}}_2·{\hat{F}}_k+\dots +\alpha {\mathcal{G}}_p·{\hat{F}}_k+\hat{Y}$$ (3)

For each node considered as a restart location the vector Ŷ is set to the random restart probability 1 − α. Now using Equation (3) each submatrix-vector multiplication can be calculated separately in parallel and the results aggregated. Each iteration F_k+1 is normalized to unit length and used in the next iteration. In hopes to maximize memory bandwidth during the calculation, we synchronize the parallel computation at the end of each iteration rather than during it. We recommend choosing p as the number of available cores.

B. Primary Subsystems

Detect-Candidate and Local-Search

Both detecting the initial candidates and searching for nearby candidates follow the same general approach in our algorithm. The equation selects new nodes heuristically based on their RWR scores, higher scores means a higher chance of being selected. Given two nodes from 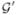the Linker computes a path connecting them. The implementation is an efficient modification of Prim's algorithm. We consider the “best path” as the path connecting the two nodes with largest RWR value when a direct link–one unused in the approximate solution–is not available. This score is the sum of RWR values over the whole length of the path.

C. Supporting Edge Attributes

In order to support edge attributes, we have chosen to embed an edge-node in each edge of . The Linegraph-Augmentation algorithm iterates over all original edges of and appends new edge-nodes to 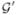. The algorithm operates in O(m) where m is the number of edges from . This is precomputed a single time before querying begins and is then used as the main input graph for querying.

This transformation creates 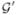, a (m + n) × (m + n) adjacency matrix. Expanding both dimensions of our adjacency matrix by a factor of m may seem expensive in memory usage; however, 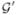is guaranteed to be bipartite between the original nodes and the new edge-nodes. Because only original nodes can be connected to edge-nodes, we have only the m × n and n × m regions of our augmented matrix that can contain values. We can derive the maximum matrix density, ρ_max, as follows: ρ_max = 2mn/(m² + 2mn + n²) if the graph is undirected only mn edges need to be stored. Because we use sparse data structures, the memory for this augmentation grows at a linear rate with the number of edges.

The matched subgraph results produced by MAGE are embedded with edge-nodes and must be converted to the original graph format. The linegraph-reverter converts the edge-nodes back to edges from as the mapping is one-to-one.

D. Supporting Multiple Attributes and Wildcards

The categorical attribute matrix 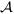is an n × t sparse matrix where there are t distinct attribute categories for each of n nodes. Each row of 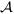represents a node while each column represents a single categorical variable. In general 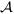is sparse so it utilizes a minor amount of memory. We support multiple attributes on each node and edge, and allow them to be selected via logical OR. The attributes are leveraged during the attribute-centric RWR carried out in line 5 of Procedure 4. By serving as restart sources during the RWR calculations, the correctly attributed nodes are given larger proximity scores and therefore are more likely to be selected as a result. Wilcards allow MAGE to effectively ignore the attribute and use the most structurally coherent node or edge during approximation. To support the wildcard attribute we have created a universal attribute applied to all nodes and edges. The function labeled Wildcard-Attribute-Inserter on line 4 of Procedure 4 works by inserting a new and distinct attribute node in the attribute matrix A that points to all nodes. When there are multiple choices to fulfill a wildcard the one with largest RWR value is selected, otherwise ties are broken by random selection.

V. Evaluation

We evaluated multiple important aspects of MAGE, such as speed, memory usage, and effectiveness on both large real and synthetic graph datasets, e.g., 460 million edge Google+ graph [12], [13]. Experimenting on real graphs allows us to better understand how MAGE works in practice, while experimenting on synthetic ones let us carefully control experimental parameters and observe MAGE's responses. Besides investigating how MAGE's speed scale with the graph size, we also study how supporting wildcards and multiple attributes in the graph queries would affect speed. All tests were run on Linux using an Intel Core i5-4670K (3.8 GHz) and 32GB of RAM.

A. Graph Datasets

Real Graphs

We have examined the scalability of our system using the attributed social network from Google+ [12], [13]. The dataset consists of four snapshots (ranging in size from 4.6M nodes, 47M edges to 28M nodes, 460M edges) each taken at different months of 2011. In order to test the practicality of MAGE, we also queried an undirected graph constructed out more than 20,000 of the Rotten Tomatoes (RT) movies in Figure 6. We used RT movie similarity to form the edges; however, MAGE operates on categorical attributes, so continuous fields must be encoded categorically by any approach to discretize continuous fields; we used quartiles.

Fig. 6.

Rotten Tomatoes queries and results. Nodes are movies; an edge connects two similar movies. Edge classes (see legend) were derived from user-contributed similarity scores. Exact matches are in green, partial matches in purple.

Synthetic graphs

We used stochastically generated Erdős-Rényi (ER) random graphs (parameterized by the number of nodes n and edges m) and Watts-Strogatz (WS) graphs (parameterized by the number of nodes n, the node degree k, and the rewiring probability p) [14], [15]. All WS graphs used p = .01 rewiring chance. Their attributes were chosen uniformly at random.

B. Scalability and Speed

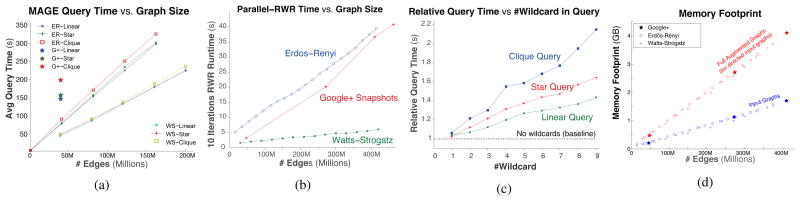
RWR requires two parameters; the fly-out or restart-probability and the number of iterations, which we set to 0.15 and 10 respectively. MAGE performs queries in linear time with the number of edges in each graph. For both synthetic graph types, the increase in query time is linear in the number of edges, suggesting good scalability. Three general query structures are explored for various sizes of graph; a 5-node 4-edge linear query, a 5-node 4-edge star, and a 5-node clique.

1) RWR Results

The timely calculation of RWR values are essential to the MAGE algorithm. We test our approach on synthetic graphs and various G+ snapshots. The synthetic graphs were generated with increasing numbers of edges. Each measurement is an average of the runtime for multiple networks at each m. The results for our parallelized RWR implementation are presented in Figure 5b. The ER graphs exhibit worse performance than WS graphs due to the constant random memory accesses during the parallelized matrix multiplication. Our experimental results, both on real and synthetic graphs suggest excellent scalability of the core RWR algorithm.

Fig. 5.

(a) MAGE query time on real and synthetic graphs of varying sizes for a linear, star, and clique query. The average query time, over 10 runs, increases linearly with the (augmented) graph's size for each query type. (b) The runtimes for 10 iterations of the random walk with restart module over Erdős-Rényi, Watts-Strogatz, and Google+ graphs of varying sizes, which increase linearly with the number of edges, even into several hundred millions nodes and edges. (c) The relative response time for queries containing wildcards tested on an Erdős-Rényi graph with 10M nodes and edges, compared against the baseline query without wildcard (horizontal black dotted line). Query time is linear in the number of wildcards in the query. (d) MAGE memory usage for Erdős-Rényi and Google+ graphs, before and after edge augmentation, which increases linearly with the number of edges.

2) Wildcard and Multi-attribute Cost

We tested the overhead introduced by increasing the number of wildcards in a fixed set of queries. Figure 5c shows the query time, when using wildcards, relative to a query with only normal attributes. The wildcard overhead increases linearly with each new wildcard, suggesting that large queries can safely incorporate wildcards.The queries used were a 6-node linear query, a 6-node star and a 5-clique. Each data point is an average over multiple runs where the wildcards were assigned at random over edges and nodes. Multi-attributes are represented as multiple 1's in and can be easily added for little overhead. Data-rich graphs can be queried in MAGE with minor increases in query latency and memory footprint.

C. Memory Usage

We performed an experiment to measure the memory usage of edge-augmentation, a memory-intensive step. In the directed case the full augmented matrix must be stored; however, in the undirected case only half of the matrix is necessary. In Figure 5d, we compare the memory footprint of each graph before and after edge augmentation (as previously explained in Secton IV-C) for graphs of increasing size.

D. Effectiveness

Measuring the effectiveness of approximate graph queries is a nontrivial task with two major challenges. The first problem stems from measuring similarity between the result and query, considering both structure and attributes. The second challenge is that the usefulness of a result is highly subjective. Human evaluation will be important in proving the overall effectiveness of our approach and we plan to perform it in our future work.

Method

Taking inspiration from related pattern matching work (e.g., [16]), we chose to modify graphs by injecting new patterns into them and then seeking those patterns with MAGE. We tested our approach against synthetic graphs and the RT movie graph. The synthetic graphs were generated as before (see Section V-A); however, the patterns were generated with 6 edge and 12 node attributes, which were assigned randomly during graph generation. In the RT graph, attributes were randomly sampled from the empirical distributions. In Table II, we present 5 general query types: (i) a short line of 6 nodes, (ii) a long line of 15 nodes, (iii) a star with 15 spokes, (iv) a barbell with two 3-cliques connected by a path of length 3, and (v) a 7-clique [1].

Table II.

The similarity between the query and first 20 results. The λ similarity is a modification of the Jaccard index. Values close to 1 mean the results matched exactly, while lower scores mean a worse approximation. MAGE produces results with high similarity to the query.

Graph Type	Query Shape	% Extra Nodes	% Extra Edges	A Score
Erdős-Rényi (ER)	Line (short)	11 ± 0.7	14 ± 0.9	0.89
	Line (long)	20 ± 0.8	26 ± 1.1	0.81
	Barbell	18 ± 0.7	18 ± 0.6	0.84
	Star	39 ± 0.8	44 ± 1.1	0.71
	Clique	64 ± 1.8	17 ± 0.1	0.77
Rotten Tomatoes (RT)	Line (short)	66 ± 1.8	30 ± 1.3	0.73
	Line (long)	84 ± 1.6	87 ± 2.2	0.54
	Barbell	96 ± 2.9	95 ± 1.9	0.51
	Star	104 ± 2.8	109 ± 2.6	0.50
	Clique	110 ± 3.4	103 ± 4.9	0.49

Table II displays the average %-difference in size between the queries and their matches over the top 20 results. We measure the quality of results using λ, a modified Jaccard Index over categorical variables which was used in [17]. We compose the λ-similarity by taking the size of the set-intersection of nodes and edges from the query with the result and normalize it by the size set-union of the same query-result pair. When a result closely matches the query, λ → 1, if the result has either extra nodes or nodes with different attributes then λ < 1.

MAGE's goal is to detect approximate matches to a user's desired query; Table II shows that the algorithm is capable of extracting results with good similarity. The WS graphs work well with linear queries, because their construction guarantees consistent paths. The RT queries generally perform worse than the synthetic graphs, because the RT contains several very low occurrence attributes that often require an approximation include, decreasing the λ-similarity. Detecting exact and approximate cliques is a very challenging problem. When discovering initial candidate nodes for the results, MAGE may pick a structurally coherent (likely to be a clique) match, but with only some exactly matched attribute nodes. This means that some of the edges or nodes of the result will not be directly connected and will introduce some new nodes and edges. Even with the complexity of approximating 7-clique MAGE is still able to return good approximations, albeit with many extra nodes and edges, demonstrating MAGE's main strength is in finding approximate matches to help the user explore different hypotheses.

For the purposes of demonstrating the semantic result quality, we present visualized query results from the RT movie data in Figure 6. To demonstrate MAGEs effectiveness, our evaluation used multiple graphs, including a real RT movie similarity graph, where MAGE finds movies matching interesting criteria (e.g., finding a cult movie that has horror and comedy ingredients). MAGE was able to find the movie Carrie that fits this query (see Fig 12, bottom row), which is mostly horror, with a few funny scenes; it indeed generated a cult following. Similarly, we also used MAGE to find movies that occupy the intersect of the genres of drama, sci-fi and action (as seen in Figure 6, top row) and it returned two popular films Underworld and Beowolf that fit this description very well. This experiment with the RT graph suggests that MAGE has the potential to be used in consumer-facing, main-stream applications such as movie recommendation.

VI. Related Work

Our work draws from several research areas including, subgraph matching, graph similarty, and graph databases. Methods in indexing have been proposed to improve the capabilities and responsiveness of graph query tools [18]. Some graph proximity measures include random-walk based approaches [19], [20], conductance-based approaches [21], and meta-path based approaches [22], [23], among others.

Matching attributed graphs has been studied in [24] again as an approach for the intelligence industry. With this idea an analyst to specify a particular pattern in an attributed relational graph and scour a much larger dataset for occurrences of such a structure. Approximate matching is a common relaxation to the subgraph isomorphism problem and has been researched heavily [2], [3].

There are a host of purely structural graph matching systems exploring polynomial time solutions to variants of the subgraph isomorphism problem [25]-[27]. These approaches generally do not utilize any semantic content from the graphs themselves, making it challenging for these approaches to extend fully to our problem formulation.

There are few algorithms that combine the aforementioned techniques to tackle inexact matching in large, attributed graphs with highly variable content. Recent works include [7] and [4], however the former requires the user to specify a “focus”node in the query and the latter returns results that do not adhere to the query structure. The closest work is that by Tong et al. [1], which proposes graph X-ray or G-Ray, a method that finds approximate subgraphs. G-Ray uses RWR to estimate the quality of a match between a subgraph and a query graph [19] which is used to rank the results extracted from the graph. G-Ray also uses the CenterPiece Subgraphs idea [11]. The main drawback of G-Ray is that it only supports graphs with node attributes. This is a significant limitation, considering the additional semantics contributed to the graphs by the edge attributes. We have leveraged some of the ideas and techniques proposed in this work to create MAGE.

VII. Conclusion

To the best of our knowledge, MAGE is the first approach that supports exact and approximate subgraph matching on graphs with both node and edge attributes, for which wildcards and multiple attribute values are permissible. Our experiments on large real and synthetic graphs (e.g., 460M edge Google+ graph) demonstrate that MAGE is both effective and scalable. Using multiple node or edge attributes in a query incurs negligible costs, and MAGE scales linearly with the number of wildcards. To demonstrate MAGE's generalizability, our effectiveness evaluation used multiple graphs, including a real Rotten Tomatoes movie similarity graph, where MAGE finds movies matching interesting criteria (e.g., finding a cult movie that has horror and comedy ingredients). We believe MAGE can be a helpful tool for exploring large, real-world graphs.

Fig. 3.

An overview of the approach used in finding an approximate subgraphs.

Fig. 4. Detailed MAGE Algorithm.