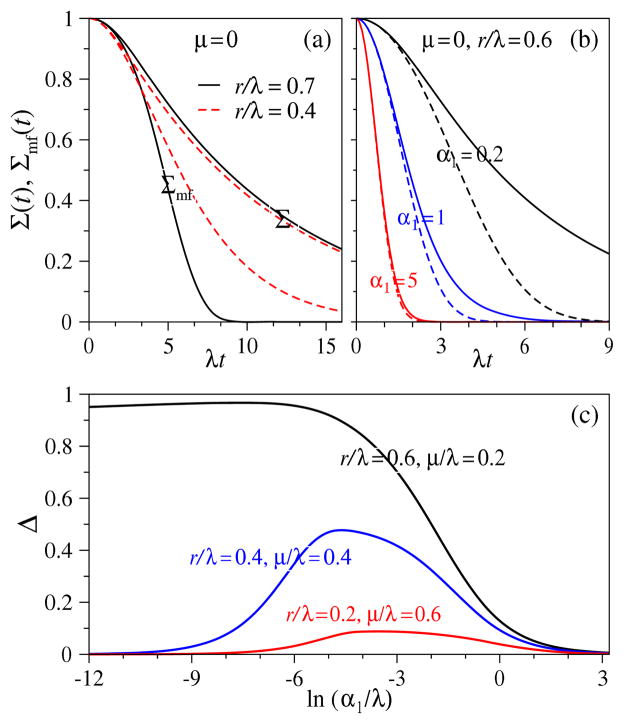
Figure 5.

Comparison between exact solutions and mean-field approximations for L = 1. (a) Σ(t) and Σ_mf (t) for μ = 0 and r/λ = 0.7 (solid) and r/λ = 0.4 (dashed). As expected, differences are larger for larger values of r/λ, where survival probability and the mean occupation 〈n₁(t)〉 share more correlations. (b) Σ(t) (solid) and Σ_mf (t) (dashed) for different values of single-particle immigration α₁ and fixed α₂ = μ = 0, r/λ = 0.6, and (p + q + ν)/λ = 0.4. The difference is largest for smaller α₁ where immigration is rate limiting, and the first arrival at the absorbing state k = 2 is more likely from particles that have replicated at k = 1. (c) Relative errors of MFPTs Δ ≡ (T − T_mf)/T as a function of α₁ for the combinations of r/λ, μ/λ indicated. When rates of nonlinear processes (r in this case) are large, the error is large. In the limit of vanishing r/λ, mean-field theory becomes exact and Δ vanishes.