Figure 1.

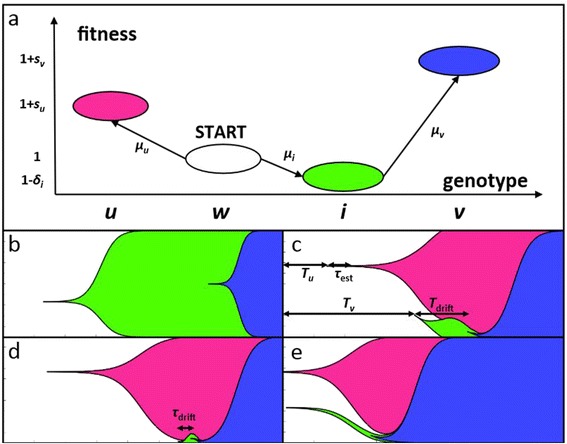
Model and characteristic trajectories. (a) The model to study fitness valley crossing prevalence. The population starts as wild type (w), and then acquires uphill mutations (u) at rate μ _u that confer an immediate fitness advantage s _u, and acquires deleterious fitness valley intermediates (i) at rate μ _i with fitness deficit δ _i on which background double-mutants (v) with fitness s _v>s _u arise at rate μ _v. (b)-(e) The four main forms of fitness valley crossing. (b) Small populations are characterized by low genetic diversity and strong genetic drift, leading sequential fixation of intermediates to dominate the dynamics. (c) For larger populations, genetic diversity is maintained longer, and double mutants will tend to arise on transient single-mutant backgrounds, in a process known as stochastic tunneling. (d) If the drift time is small compared to the maximal rate of change in background fitness, we can approximate the drift time of the intermediate by its expectation, dramatically simplifying the mathematical analysis. (e) For very large populations, we can treat single-mutants deterministically, in a process dubbed semi-deterministic tunneling.