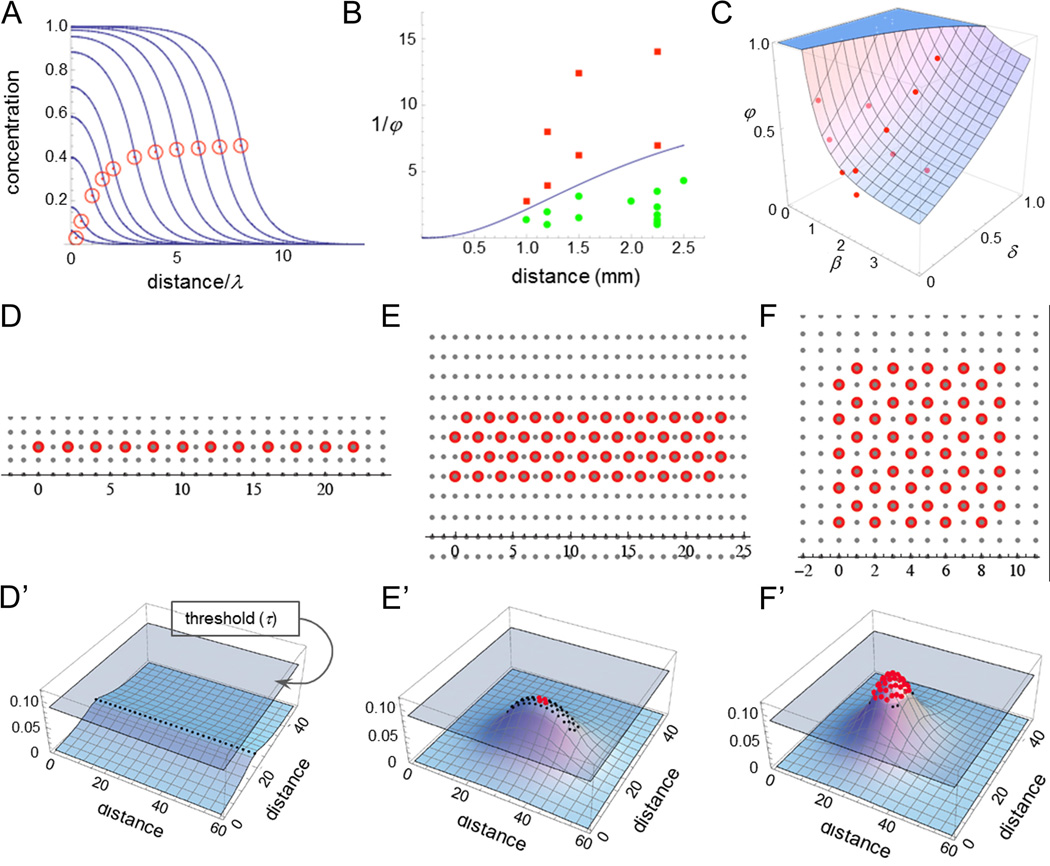
Fig. 2. Mathematical modeling identifies the decay length of a putative quorum signal.

(A) Calculated steady state concentrations for a diffusible substance produced within injury fields in proportion to the numbers of plucked HF. Each curve represents a different sized circular injury field, with the red circle placed at the value on the abscissa corresponding to the injury field radius, in units of the diffusing substance decay length. Specifically, the 11 curves represent increasing field sizes of 0.25, 0.5, 1, 1.5, 2, 3, 4, 5, 6, 7 and 8 decay lengths. As plucked regions grow larger, the value at the boundary asymptotes to one half the value at the center. λ is a decay length. Please see Results and supplements for more explanation. (B) Data from a variety of regeneration experiments involving circular wound fields are plotted as a function of the inverse of the plucked fraction (φ) and the radius of the wound field. The curve drawn between the points corresponding to cases of successful (green) and unsuccessful (red) regeneration was obtained from the equations that produced the curves in panel A, by fitting two parameters, the decay length and the threshold concentration for regeneration. The range of possible values consistent with the data was manually explored to yield a range of decay length estimates. (C) The same model was used as in panel B, but the data that were fit consisted of the distances, δ, just beyond the edges of injury fields at which initial regeneration was seen. (β, radius of the injury field; φ, the plucked fraction). The plotted surface represents a least-squares best fit to the data. (D–F, D’–F’) Effects of injury field shape. 50 hairs were plucked evenly, at a density of every other hair, either in a straight line (D, D’), a narrow rectangle (6:1 aspect ratio; E, E’) or a square (F, F’). In D’–F’, a discrete form of the equation used in panels A–C, in which each HF is modeled as a discrete source, was used to plot the steady-state spatial distributions of a distressor released by plucked follicles (distances are plotted in units of the inter-follicular distance, about 0.15 mm). Wherever plotted surfaces extend above a regeneration concentration threshold (grey plane), red dots mark the location of each HF indicating successful regeneration. The requirement that these curves be consistent with the observed regeneration patterns in all three cases was sufficient to provide yet a third estimate of the distressor decay length. See also supplement on mathematical model.