A regression tree approach to identifying subgroups with differential treatment effects

Abstract

In the fight against hard-to-treat diseases such as cancer, it is often difficult to discover new treatments that benefit all subjects. For regulatory agency approval, it is more practical to identify subgroups of subjects for whom the treatment has an enhanced effect. Regression trees are natural for this task because they partition the data space. We briefly review existing regression tree algorithms. Then we introduce three new ones that are practically free of selection bias and are applicable to data from randomized trials with two or more treatments, censored response variables, and missing values in the predictor variables. The algorithms extend the GUIDE approach by using three key ideas: (i) treatment as a linear predictor, (ii) chi-squared tests to detect residual patterns and lack of fit, and (iii) proportional hazards modeling via Poisson regression. Importance scores with thresholds for identifying influential variables are obtained as by-products. A bootstrap technique is used to construct confidence intervals for the treatment effects in each node. The methods are compared using real and simulated data.

1 Introduction

For many diseases, such as cancer, it is often difficult to find a treatment that benefits all patients. Current thinking in drug development is to find a subject subgroup, defined by individual characteristics, that shows a large treatment effect. Conversely, if a treatment is costly or has potential negative side effects, there is interest to look for subgroups for which it is ineffective. This problem of searching for subgroups with differential treatment effects is known as subgroup identification [1–3].

To fix ideas, suppose that the response variable Y is uncensored and the treatment variable Z takes values l = 1, 2, . . . , L. Let X denote a vector of covariates. Given a subgroup S defined in terms of X, let R(S) = max_i,j |E(Y |Z = i, S) − E(Y| Z = j, S)| denote the effect size of S. The goal is to find the maximal subgroup with−the largest value of R(S), where the size of S is measured in terms of its probability of occurrence P(S). If Y is subject to censoring, we replace the mean of Y by the log-hazard rate so that R(S) is the largest absolute log-hazard ratio between any two treatments.

Consider, for example, data from a randomized trial of the German Breast Cancer Study Group [4, 5] with 686 subjects where the response is recurrence-free survival time in days. The trial was designed as a 2 × 2 factorial comparing 3 vs. 6 cycles of chemotherapy and presence vs. absence of hormone therapy, but the data contain no information on the number of cycles, presumably because it was previously found not significant [6]. Median follow-up time was nearly 5 years and 387 subjects did not experience a recurrence of the disease during the trial (54 percent censoring). The variables are hormone therapy (horTh: yes, no), age (21–80 years), tumor size (tsize: 3–120 mm), number of positive lymph nodes (pnodes: 1–51), progesterone receptor status (progrec: 0–2380 fmol), estrogen receptor status (estrec: 0–1144 fmol), menopausal status (menostat: pre, post), and tumor grade (tgrade: 1, 2, 3). A standard proportional hazards regression model finds hormone therapy to have a significant positive effect on survival, with and without adjusting for the covariates [7, 8]. It is interesting, however, to find out if a subgroup exists where the treatment has no effect.

Parametric and semi-parametric models such as the proportional hazards model do not easily lend themselves to this problem. Besides, if there are more variables than observations, such as in genetic data, these models cannot be used without prior variable selection. Regression tree models are good alternatives, because they are nonparametric, naturally define subgroups, scale with the complexity of the data, and are not limited by the number of predictor variables.

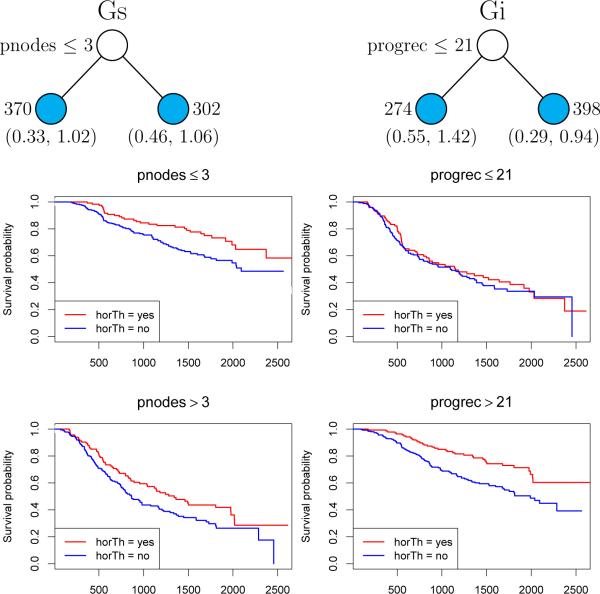
Following current medical literature [9, 10], we call a variable prognostic if it provides information about the response distribution of an untreated subject. That is, it has marginal effects on the response but does not interact with treatment. Examples are age, family history of disease, and prior therapy. A variable is predictive if it defines subgroups of subjects who are more likely to respond to a given treatment. That is, it has interaction effects with the treatment variable. Figure 1 shows two regression tree models and the Kaplan-Meier curves in the terminal nodes of the trees. In the Gs model on the left, variable pnodes is prognostic: recurrence probability is reduced if pnodes > 3, with and without treatment. In the Gi model on the right, variable progrec is predictive: hormone therapy has little effect if progrec ≤ 21 and an enhanced effect otherwise.

Figure 1.

Gs (left) and Gi (right) tree models and Kaplan-Meier curves for breast cancer data. At each intermediate node, an observation goes to the left child node if and only if the displayed condition is satisfied. Sample sizes are beside terminal nodes; 95% bootstrap confidence intervals of relative risks for therapy versus no therapy are below nodes.

The main goal of this article is to introduce the algorithms that yield the models in Figure 1 and to compare them against existing solutions, which are briefly reviewed in Sec. 2. Sec. 3 presents the new algorithms for uncensored response variables. Sec. 4 compares the selection bias and accuracy of the new and old methods and Sec. 5 proposes a bootstrap technique for computing confidence intervals of treatment and other effects in the subgroups. Sec. 6 extends the algorithms to censored survival data and Sec. 7 obtains importance scores for ranking the variables and and thresholds for identifying the unimportant ones. Sec. 8 gives an application to a retrospective candidate gene study where there are large numbers of missing values and Sec. 9 concludes the article with some closing remarks. It is assumed throughout that the data are obtained from randomized experiments (see, e.g., Su et al. [11] for regression tree models for observational data).

2 Previous work

Let u_i and x_i denote the (actual but possibly unobserved) survival time and covariate vector of subject i. Let s_i be an independent observation from some censoring distribution and let δ_i = I(u_i < s_i) be the event indicator. The observed data vector of subject i is (y_i, δ_i, x_i), where y_i = min(u_i, s_i), i = 1, 2, . . . , n. Let (y, x) denote the hazard function at x = (x₁, x₂, . . . , x_M). The proportional hazards model specifies that λ(y, x) = λ₀(y) exp(η), where λ₀(y) is a baseline hazard and η = β′x is a linear function of the covariates.

Assuming that the treatment has two levels (denoted by z = 0, 1), one approach [12] splits each node t into left and right child nodes t_L and t_R to maximize the Cox partial likelihood ratio statistic for testing H₀ : λ(y, x) = _0,t(y) exp{β₀zI(x ∈ t)} against H₁ : λ(y, x) = λ_0,t(y) exp{β₁zI(x ∈ t_L) + β₂zI(x ∈ t_R). A related approach, called interaction trees (IT) [13, 14], chooses the split that minimizes the p-value from testing H₀ : β₃ = 0 in the model λ(y, x) = λ_0,t(y) exp{β₁z + β₂I(x ∈ t_L) + β₃zI(x ∈ t_L)}. If there is no censoring, the model is E(y) = β₀+β₁z+β₂I(x ∈ t_L)+β₃zI(x ∈ t_L). Both methods employ the greedy search paradigm of evaluating all splits t_L = {x_j ∈ S} and t_R = {x_j ∉ S} on every x_j and every S, where S is a half line if x_j is ordinal and is a subset of values if x_j is categorical. As a result, they are computationally expensive and biased toward selecting variables that allow more splits. Further, because λ_0,t(y) is a function of t and hence of x, the tree models do not have proportional hazards and regression coefficients in different nodes cannot be compared.

Given a binary response variable Y = 0, 1, the virtual twins (VT) method [2] first uses a random forest [15] model, with Z,X₁, . . . ,X_M, ZX₁, . . . , ZX_M, (1 − Z)X₁, . . . , (1 − Z)X_M as split variables, to estimate the treatment effect τ = P(Y = 1 | Z = 1) − P(Y = 1 | Z = 0) of each subject. Categorical variables are converted to dummy 0-1 variables for splitting. Then RPART [16] is used to construct a classification or regression tree model to predict τ for each subject and to obtain the subgroups. If a classification tree is used, the two classes are defined by the estimated τ being greater or less than a pre-specified constant; if a regression tree is used, the subgroups are the terminal nodes with estimated τ greater than a pre-specified constant. Although the basic idea is independent of random forest and RPART, their use results in VT inheriting all their weaknesses, such as variable selection bias and (for random forest) lack of a preferred way to deal with missing values.

The subgroup identification based on differential effect search (SIDES) method [3] finds multiple alternative subgroups by identifying the best five (default) splits of each node that yield the most improvement in a desired criterion, such as the p-values of the differential treatment effects between the two child nodes, the treatment effect size in at least one child node, or the difference in efficacy and safety between the two child nodes. For each split, the procedure is repeated on the child node with the larger improvement. Heuristic and resampling-based adjustments are applied to the p-values to control for multiplicity of splits and correlations among the p-values. The method appears to be most useful for generating candidate subgroups with large differential effects, but because only variables that have not been previously chosen are considered for splitting each node, the method may not be effective if the real subgroups are defined in terms of interval sets of the form {a_j < X_j ≤ b_j}.

Most methods can control the minimum node sample size so that the subgroups have sufficient numbers of observations. The qualitative interaction tree (QUINT) method [17] deals with this directly by optimizing a weighted sum of a measure of effect size and a measure of subgroup size. It looks for “qualitative interactions,” where one treatment performs better than another in one subgroup and worse in another subgroup. Like the above methods, QUINT finds the subgroups by searching over all possible splits on all predictor variables and hence is subject to selection bias in its splits. QUINT is currently limited to ordinal X_i and uncensored Y variables. All the methods are limited to two-level treatment variables.

3 Uncensored data

It is well known that evaluating all possible splits on all variables to optimize an objective function leads to a bias toward selecting variables that allow more splits [18–20]. This is due to an ordinal variable with k unique values yielding k − 1 splits and a categorical variable with the same number of unique values yielding 2^k−1 −1 splits. As a result, a variable that allows more splits has a greater chance to be selected than one with fewer splits. Besides increasing the chance of spurious splits, the bias can undermine the credibility of the results. SIDES tries to control the bias with Bonferroni-type adjustments, but this can lead to over correction, as in the CHAID [21] classification tree algorithm, which is biased toward selecting variables with few splits.

The GUIDE algorithm [19, 22] overcomes this problem by using a two-step approach to split selection: first find the split variable and then search for the best split on the selected variable. The first step yields substantial computational savings, because there is no need to find the best split on each of the other variables. It also eliminates selection bias, at least in principle, by using chi-squared tests to select the split variable. QUEST [18], CRUISE [23], CTREE [24], and MOB [25] are other algorithms that employ significance tests for variable selection. In this section we introduce three ways to extend GUIDE to subgroup identification for the case where Y is not censored.

3.1 Gc: classification tree approach

This method requires that Y and Z are binary, taking values, 0, and 1, say. Then a classification tree may be used to find subgroups by defining the class variable as V = Y +Z mod 2:

$$V=\{\begin{array}{cc}0,\hfill & \text{if}\{Y=1\text{and}Z=1\}\text{or}\{Y=0\text{and}Z=0\},\hfill \\ 1,\hfill & \text{if}\{Y=0\text{and}Z=1\}\text{or}\{Y=1\text{and}Z=0\},\hfill \end{array}\phantom{\}}$$

This is motivated by the observation that the subjects for which V = 0 respond differentially to treatment and those for which V = 1 do not. Thus a classification tree constructed with V as the response variable will likely identify subgroups with differential treatment effects. Although any classification tree algorithm may be used, we use GUIDE [22] here because it does not have selection bias, and call it the Gc method (“c” for classification).

3.2 Gs and Gi: regression tree approach

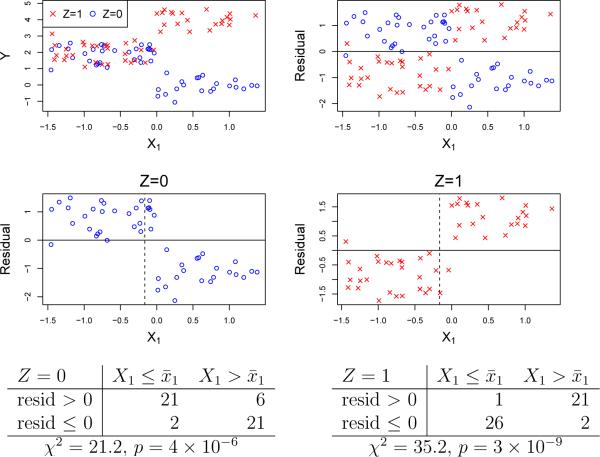
GUIDE linear regression tree [19] offers an alternative approach that permits Y and Z to take more than two values each. At each node, we fit a model linear in Z (with dummy coding) and select a variable to split by examining the residual pattern for each level of Z. Suppose, for example, that data (X₁, X₂, . . . , Y, Z) are generated from the model

$$Y=1.9+0.2I(Z-1)-1.8I(X_1>0)+3.6I(X_1>0,Z=1)+\epsilon$$ (1)

where Z = 0, 1 and ε is independent normal. The true subgroup being X₁ > 0, we should split the data using X₁. Figure 2 shows how this conclusion can be reached by looking at the data. The top row plots Y and the residuals from fitting the model EY = β₀ + β₁Z. The middle row plots the residuals vs. X₁ for each level of Z. The opposite trends in the residual plots indicate that X₁ has an interaction with Z. No other X variable shows such strong patterns. We can quantify the strength of the interaction by forming a contingency table with the residual signs as rows and grouped values of X₁ (obtained by dividing its values at the sample mean) as shown in the bottom row of the figure and summing the chi-squared statistics over the levels of Z. By applying this procedure to each X_i, we can rank the variables and select the one with the largest summed chi-squared to split the data. We call this the Gs method (“s” for sum).

Figure 2.

Plots of Y and residuals vs. X₁ after fitting EY = β₀+ β₁Z to data from model (1); vertical dashed lines indicate sample mean of X₁

Contingency table tests are convenient because they are quick to compute, can detect a large variety of patterns, and are applicable to categorical X variables, where we use their values for the columns. Because the latter changes the degrees of freedom (df) of the chi-squared statistics, we need to adjust for differences in df before summing them. We do this by following GUIDE which uses a double application of the Wilson-Hilferty approximation [26] to convert each contingency table chi-squared statistic to a 1-df chi-squared quantile. Specifically, let x and y be chi-squared quantiles with ν df and μ, respectively, degrees of freedom. Then [22]

$$y\approx \mu {\left[1-2∕\left(9\mu \right)+\sqrt{\nu ∕\mu }\{{(x∕\nu )}^{1∕3}-1+2∕\left(9\nu \right)\}\right]}^3.$$ (2)

The approximation provides a ranking of the variables without the need for chi-squared p-values that can be extremely small and hard to compute accurately. After a variable is selected, a search is carried out for the best split on the variable that minimizes the sum of squared residuals in the two child nodes and the process is applied recursively to each node. One distinct advantage of contingency tables is that missing values can be dealt with easily as detailed in the following algorithm.

4 Bias and accuracy

4.1 Selection bias

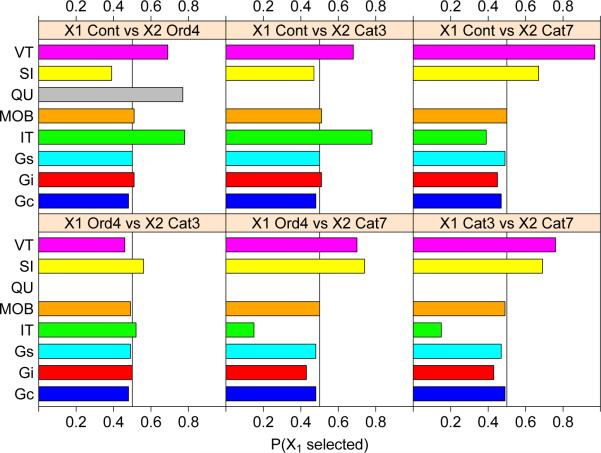
It is obviously important that a tree model not have selection bias if it is used for subgroup identification. At the minimum, this requires that if all the variables are independent of Y, each X_i has the same probability of being selected to split each node. We carried out a simulation experiment to compare the methods on this property. The experiment employed two predictors, X₁ and X₂, and Bernoulli response and treatment variables Y and Z each with success probability 0.50. All variables are mutually independent. The distributions of X₁ and X₂ ranged from standard normal, uniform on the integers 1–4, and equi-probable categorical with 3 and 7 levels, as shown in Table 1.

Table 1.

Four types of distributions of X₁ and X₂.

Notation	Type	Distribution
Cont	Continuous	Standard normal
Ord4	Ordinal	Discrete uniform with 4 levels
Cat3	Categorical	Discrete uniform with 3 levels
Cat7	Categorical	Discrete uniform with 7 levels

Based on 2500 simulation iterations with a sample size of 100 in each iteration, Figure 4 shows the frequency that each method selects X₁ to split the root node. Simulation standard errors are less than 0.01. An unbiased method should select X₁ or X₂ with equal probability regardless of their distributions. The results show that IT, QUINT, SIDES and VT have substantial selection biases (QUINT is limited to ordinal X_i). IT and QUINT are biased towards selecting the variable that has more splits while SIDES and VT are the opposite. In contrast, the selection frequencies of Gc, Gs, and MOB are all within three simulation standard errors. The frequencies of Gi are also within three standard errors, except when X₂ is categorical with 7 levels where it has a slightly higher chance to be selected.

Figure 4.

Simulated probabilities that X₁ is selected to split the root node; simulation standard errors less than 0.01. A method is unbiased if it selects X₁ with probability 0.50. SI and QU refer to SIDES and QUINT, respectively. The latter is not applicable to categorical variables.

4.2 Accuracy

We use three simulation models to compare the methods in terms of their accuracy in selecting the correct variables and the correct subgroups. Each model employs a binary treatment variable Z with P (Z = 0) = P (Z = 1) and 100 variables X = (X₁, X₂, . . . , X₁₀₀), all mutually independent. Each X_i takes categorical values 0, 1, or 2 (simulating genetic markers with genotypes AA, Aa, and aa), with X₁ and X₂ having identical marginal distribution P (X₁ = 0) = 0.4, P (X₁ = 1) = 0.465 and P (X₁ = 2) = 0.135. The others have marginal distributions P (X_j = 0) = (1 − π^j)², P (X_j = 1) = 2π_j(1 − π_j) and $P(X_j=2)={\pi }_j^2$ with π_j (j = 3, 4, . . . , 100) independently simulated from a beta distribution with density f(x) ∝ x(1 − x)². The models for Y are:

• M1: P (Y = 1 | X) = 0.4 + 0.05I(Z = 1){4I(X₁ 6= 0) + 3I(X₂ 6= 0) + I(X₁ 6= 0, X₂ 6= 0)}

• M2: P (Y = 1 | X) = 0.3 + 0.2[{2I(Z = 1) − 1}I(X₁ 6= 0, X₂ 6= 0) + I(X₃ 6= 0) + I(X₄ 6= 0)]

• M3: P (Y = 1 | X) = 0.5 + 0.1[2{I(Z = 1) + I(X₁ 6= 0) + I(X₂ 6= 0)} − 3].

Figure 5 shows the values of P (Y = 1 | X) for models M1 and M3. Variables X₁ and X₂ are predictive in M1 but prognostic in M3. Figure 6 shows the values for model M2 which is more complex; X₁ and X₂ are predictive and X₃ and X₄ are prognostic. M2 tests the ability of a method to distinguish between prognostic and predictive variables.

Figure 5.

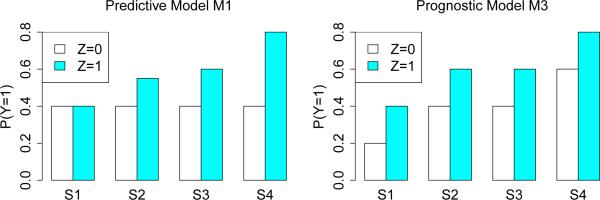
Models M1 and M3. Sets S1 = {X₁ = 0, X₂ = 0 , S2 = {X₁ = 0, X₂ > 0}, S3 = {X₁ > 0, X₂ = 0}, and S4 = {X₁ > 0, X₂ > 0}.

Figure 6.

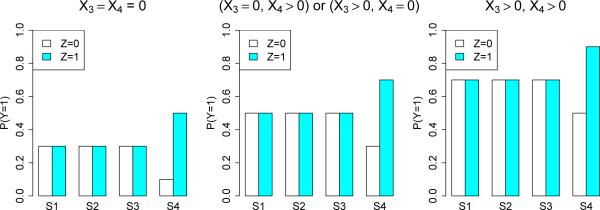
Model M2, with predictive X₁ and X₂ and prognostic X₃ and X₄. Sets S1 = {X₁ = 0, X₂ = 0}, S2 = {X₁ = 0, X₂ > 0} and S3 = {X₁ > 0, X₂ = 0}, and S4 = {X₁ > 0, X₂ > 0}

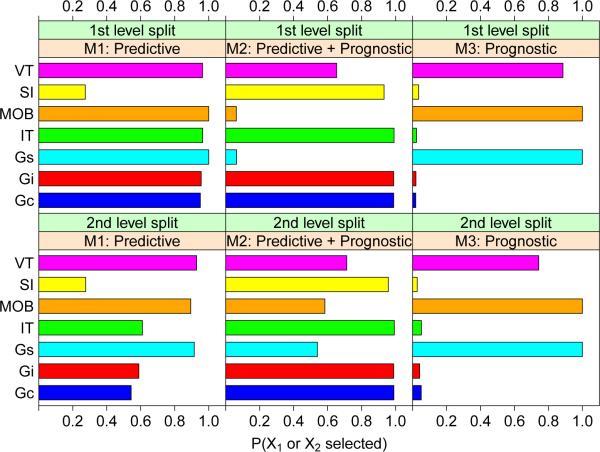
First we compare the frequencies that X₁ and X₂ are chosen at the first two levels of splits of a tree. For each of 1000 simulation iterations, 100 observations of the vector (X, Y, Z) are simulated from each model and a tree is constructed using each method. The frequencies that X₁ or X₂ is selected to split the root node (1st level split) as well as one or both of its child nodes (2nd level split) are graphed in Figure 7. QUINT is excluded because it does not allow categorical variables. The AIC pruning penalty is used instead of the default BIC for IT because the the AIC yields trivial trees less often.

Figure 7.

Probabilities that X₁ or X₂ are selected at first and second level splits of trees for models M1, M2, and M3. Long bars are better for M1 and M2, and short bars are better for M3. SI stands for SIDES.

For model M1, where X₁ and X₂ are predictive and there is no other variable associated with Y , all but SIDES select X₁ or X₂ to split the root node with comparably high frequency. At the second split level, the frequencies of Gs, MOB, and VT are distinctly higher than those of Gc, Gi, and IT, while that of SIDES remains low. Therefore Gs, MOB, and VT are best and Gc, Gi and IT second best for model M1 on this criterion. The situation is different in M2 which has two predictive and two prognostic variables. Now Gc, Gi, and IT are excellent with SIDES close behind and Gs and MOB are very poor. This shows that the latter two do not distinguish between predictive and prognostic variables. This is confirmed in M3 which has no predictive variables. Here the probability that X₁ or X₂ is selected to split the nodes should not be different from that of the other 98 variables, but Gs, MOB and VT pick the former with high frequencies. Only Gc, Gi, IT, and SIDES perform reliably in this case.

Next we compare the power of the methods in identifying the correct subgroup. Let S be any subgroup. Recall from the Introduction that the effect size is R(S) = |P (Y = 1 | Z = 1, S) − P (Y = 1 | Z = 0, S)|. The “correct” subgroup S* is defined as the maximal (in probability) subgroup S with the largest value of R(S). For models M1 and M2, S* = {X₁ ≠ 0, X₂ ≠ 0}; for M3, S* is trivially the whole space because the effect size is constant.

To estimate accuracy, let n(t, y, z) denote the number of training samples in node t with Y = y and Z = z and define $n(t,+,z)={\sum }_{y}n(t,y,z)$ and $n_t={\sum }_{z}n(t,+,z)$. Let S_t be the subgroup defined by t. The value of R(S_t) is estimated by R̂_(St) = n(t, 1, 1)/n(t, +, 1) − n(t, 1, 0)/n(t, +, 0)|. The estimate Ŝ of S* is the subgroup S_t such that R̂_(St) is maximum among all terminal nodes. If Ŝ is not unique, we take their union. The “accuracy” ofŜ is defined to be P (Ŝ_)/P (S*) if Ŝ ⊂ S* and 0 otherwise.

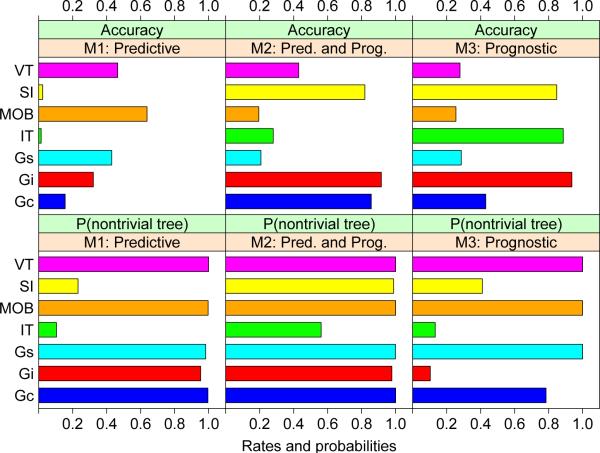
Table 2 and Figure 8 show the estimated accuracies and probabilities of nontrivial trees based on samples of size 100 and 1000 simulation iterations. We see that:

• Model M1. MOB, VT, Gs, and Gi are best, in that order. IT and SIDES have very low accuracy, due to their high tendency to yield trivial trees and hence no subgroups. The other four methods almost always give nontrivial subgroups.

• Model M2. Gi has the highest accuracy, at 0.91, followed by Gc and SIDES at 0.86 and 0.82, respectively. Gs, MOB, IT and VT have difficulty distinguishing predictive from prognostic variables; all yield nontrivial trees almost all the time, except for IT which gives a nontrivial tree 56% of the time.

• Model M3. Because S* is the whole space, the ideal tree is trivial. Gi and IT are best, yielding trivial trees 90% of the time. In terms of accuracy, Gi, IT, and SIDES are best, having values of 0.94, 0.87, and 0.85, respectively. Gs, MOB, and VT are the worst, because they produce nontrivial trees all the time.

Table 2.

Accuracy rates of subgroup selection and frequencies of nontrivial trees. Larger values are better.

Model	Type	Gi	Gs	Gc	IT	SIDES	VT
M1	Accuracy	0.322	0.430	0.150	0.015	0.024	0.465
M1	P(nontrivial tree)	0.953	0.983	0.990	0.105	0.232	1.000
M2	Accuracy	0.913	0.204	0.855	0.280	0.819	0.430
M2	P(nontrivial tree)	0.979	0.999	1.000	0.562	0.988	1.000
M3	Accuracy	0.939	0.285	0.519	0.886	0.848	0.279
M3	P(nontrivial tree)	0.104	1.000	0.693	0.133	0.410	1.000

Figure 8.

Accuracy rates of subgroup identification and frequencies of nontrivial trees for models M1, M2, and M3. For accuracy, long bars are better. For frequencies of nontrivial trees, long bars are better for M1 and M2 and short bars are better for M3. SI stands for SIDES.

The above results suggest that Gi is the overall best method in terms of accuracy. It is best in models M2 and M3 and fourth best in model M1, where it loses to Gs, MOB, and VT, which are more accurate when there are no prognostic variables. Gc, IT, and SIDES are dominated by Gi in all three models.

5 Bootstrap confidence intervals

Naïve point and interval estimates of the treatment means and differences can certainly be calculated from the training data in each node. Let μ(t, z) denote the true mean response for treatment z in node t and let (y_i, z_i), i = 1, 2, . . . , n_t, be the observations in t. Let k_z denote the number of observations in t assigned to treatment z. Then $\widehat{\mu }(t,z)=k_z^{-1}{\sum }_{z_i=z}{y}_i$ is the naïve estimate of μ(t, z). If $\widehat{\sigma }(t,z)$ denotes the sample standard deviation of the y_i among the treatment z observations in t, then $\widehat{\mu }(t,z)\pm 2k_z^{-1∕2}\widehat{\sigma }(t,z)$ is a naïve 95% confidence interval for μ(t, z). If Z takes only two values, let d(t) = μ(t, 1)−μ(t, 0). Then $\widehat{d}\left(t\right)=\widehat{\mu }(t,1)-\widehat{\mu }(t,0)$ is the naïve estimate of the treatment effect and a naïve confidence interval for d(t) is the usual two-sample t-interval. Because the nodes in the tree are not fixed in advance but are typically produced by a complex search procedure, however, the validity of these estimates cannot be taken for granted. For example, SIDES employs adjustments to the naïve p-values of treatment effects in the nodes to control bias.

To see the extent of the bias for Gi and Gs, we carried out a simulation experiment using models M1 and M2. The experimental design is an r-replicate (r = 2, 4) of a 3⁴ factorial in variables X₁, X₂, X₃, X₄, each taking values 0, 1, and 2, and Z independent Bernoulli with probability 0.50. The binary response Y is simulated according to models M1 or M2. In each simulation trial, a Gi or Gs tree T is constructed from the training data. If T is nontrivial, we record the average values of $\widehat{\mu }(t,z)-\mu (t,z)$ and d̂_(t) − d(t) over terminal nodes t and the proportions of times each naïve confidence interval contains the true estimand. Columns 3–8 of Table 3 show the estimated bias and coverage probabilities of the intervals over 2000 simulation trials that result in nontrivial trees. The biases are remarkably small (the true means range from 0.30 to 0.90). We attribute this to Gi and Gs not finding splits that directly maximize or minimize the treatment effect, unlike SIDES and QUINT. The coverage probabilities, on the other hand, are all too low, although there is a perceptible improvement as r increases.

Table 3.

Bias of estimated treatment means and their difference (averaged over nodes of each tree) and coverage probabilities of naïve and bootstrap 95% intervals, based on 1000 simulations trials of nontrivial trees, with 100 bootstrap iterations per trial. r is the number of replicates of a 3⁴ design.

		Bias of naïve estimates of means and difference			Coverage probabilities of 95%
					naïve intervals			bootstrap intervals
r	Expt	μ(t, 0)	μ(t, 1)	d(t)	μ(t, 0)	μ(t, 1)	d(t)	μ(t, 0)	μ(t, 1)	d(t)
2	M1-Gi	6.8E-3	−2.2E-2	−2.9E-2	0.821	0.811	0.818	0.892	0.955	0.934
	M1-Gs	4.4E-3	−1.9E-2	−2.3E-2	0.819	0.800	0.857	0.907	0.952	0.935
	M2-Gi	6.8E-3	−2.0E-2	−2.6E-2	0.835	0.846	0.836	0.937	0.947	0.941
	M2-Gs	3.5E-4	−1.5E-2	−1.5E-2	0.871	0.861	0.907	0.953	0.965	0.942
4	M1-Gi	3.0E-2	−1.6E-2	−1.9E-2	0.880	0.874	0.889	0.903	0.972	0.957
	M1-Gs	3.7E-3	−1.5E-2	−1.9E-2	0.869	0.862	0.888	0.916	0.967	0.955
	M2-Gi	1.1E-3	−7.5E-3	−8.6E-3	0.896	0.915	0.911	0.966	0.967	0.963
	M2-Gs	−3.8E-3	−9.4E-3	−5.7E-3	0.888	0.913	0.916	0.968	0.973	0.950

To obtain intervals with better coverage, we use a bootstrap method to estimate the standard deviations of the naïve estimates. Let $\mathcal{L}$ denote a given data set and let T denote the regression tree constructed from it. Let ${\mathcal{L}}_j^{\ast }(j=1,2,\dots ,J)$ be a bootstrap training sample from $\mathcal{L}$ and let $T_j^{\ast }$ be the tree constructed from ${\mathcal{L}}_j^{\ast }$ with naïve estimates ${\widehat{\mu }}_j^{\ast }(t^{\ast },z)$ for terminal nodes t* in $T_j^{\ast }$. Let $n_z(t\cap t^{\ast })$ be the number of treatment z observations from $\mathcal{L}$ that belong to $t\cap t^{\ast }$ and define

$${\stackrel{‒}{\mu }}_j^{\ast }(t,z)={\sum }_{t^{\ast }}{n}_z(t\cap t^{\ast }){\widehat{\mu }}_j^{\ast }(t^{\ast },z)∕{\sum }_{t^{\ast }}{n}_z(t\cap t^{\ast })$$

The bootstrap estimate of the variance of $\widehat{\mu }(t,z)$ is the sample variance $s_{\mu }^2(t,z)$ of $\{{\stackrel{‒}{\mu }}_1^{\ast }(t,z),{\stackrel{‒}{\mu }}_2^{\ast }(t,z),\dots ,{\stackrel{‒}{\mu }}_J^{\ast }(t,z)\}$ and a 95% bootstrap confidence interval for μ(t, z) is $\widehat{\mu }(t,z)\pm 2s_{\mu }(t,z)$. If Z takes values 0 and 1, let ${\stackrel{‒}{b}}_j^{\ast }\left(t\right)={\stackrel{‒}{\mu }}_j^{\ast }(t,1)-{\stackrel{‒}{\mu }}_j^{\ast }(t,0)$. Then a 95% confidence interval for d(t) is d̂(t) ± 2s_d(t) where $s_d^2\left(t\right)$ is the sample variance of $\{{\stackrel{‒}{d}}_1^{\ast }\left(t\right),{\stackrel{‒}{b}}_2^{\ast }\left(t\right),\dots ,{\stackrel{‒}{d}}_J^{\ast }\left(t\right)\}$.

The rightmost three columns of Table 3 give the simulated coverage probabilities of the bootstrap intervals using J = 100. There is a clear improvement over the naïve intervals. In particular, the coverage probabilities of the bootstrap intervals for the treatment effect d(t) are remarkably accurate across the two models and two methods. The worst performance occurs in model M1 for Z = 0, where the true treatment mean is 0.40 in all nodes (see Figure 5).

6 Censored data

Several obstacles stand in the way of direct extension of Gi and Gs to data with censored response variables. The obvious approach of replacing least squares fits with proportional hazards models in the nodes [12, 13] is problematic because Gs employs chi-squared tests on residuals and their signs. Although there are many definitions of such residuals [29], it is unclear if any will serve the purpose here. Besides, as noted earlier, fitting a separate proportional hazards model in each node yields different baseline cumulative hazard functions. As a result, the whole model no longer has proportional hazards and hence regression coefficients between nodes cannot be compared. To preserve this property requires a common estimated baseline cumulative hazard function. We solve these problems with the old trick of using Poisson regression to fit proportional hazards models.

Let u_i and x_i denote the survival time and covariate vector of subject i. Let s_i be an independent observation from some censoring distribution and let δ_i = I(u_i < s_i) be the event indicator. The observed data vector corresponding to subject i is (y_i, δ_i, X_i), where y_i = min(u_i, s_i), i = 1, 2, . . . , n. Let F (u, x) and (u, x) denote the distribution and hazard functions, respectively, at x. The proportional hazards model specifies that λ(u, x) = λ₀(u) exp(η), where λ₀(u) is the baseline hazard and η = β′x is a linear function of the covariates. Let $\Lambda (u,\mathbf{x})={\int }_{-\infty }^u\lambda (z,\mathbf{x})dz$ denote the cumulative hazard function and let Γ₀(u) = Γ(u, 0) be the baseline cumulative hazard. Then the density function is f(u, x) = λ₀(u) exp{η− Γ₀(u) exp(η)}. Letting μ_i = Γ₀(y_i) exp(η_i), the loglikelihood can be expressed as

$$\begin{array}{c}\sum _{i=1}^n{\delta }_i\log f(y_i,{\mathbf{x}}_i)+\sum _{i=1}^n(1-{\delta }_i)\log \{1-F(y_i,{\mathbf{x}}_i)\}\\ =\sum _{i=1}^n[{\delta }_i\{\log {\Lambda }_0\left(y_i\right)+{\eta }_i\}-{\Lambda }_0\left(y_i\right)\exp \left({\eta }_i\right)+{\delta }_i\log \{{\lambda }_0\left(y_i\right)∕{\Lambda }_0\left(y_i\right)\}]\\ =\sum _{i=1}^n({\delta }_i\log {\mu }_i-{\mu }_i)+\sum _{i=1}^n{\delta }_i\log \{{\lambda }_0\left(y_i\right)∕{\Lambda }_0\left(y_i\right)\}.\end{array}$$

The first term on the right is the kernel of the loglikelihood for n independent Poisson variables δ_i with means μ_i and the second term is independent of the covariates (see, e.g., [30, 31]). If the Γ₀(y_i) values are known, the vector β may be estimated by treating the event indicators δ_i as independent Poisson variables distributed with means Γ₀(y_i) exp(β′x_i).

Thus we can construct a proportional hazards regression tree by iteratively fitting a Poisson regression tree [32, 33], using δ_i as Poisson responses, the treatment indicators as predictor variables, and log Γ₀(y_i) as offset variable. Gi employs loglinear model goodness-of-fit tests [34, p. 212] to the fitted values to obtain the split variables and split points. At the first iteration, Γ₀(y_i) is estimated by the Nelson-Aalen [35, 36] method. After each iteration, the estimated relative risks of the observations from the tree model are used to update Γ₀(y_i) for the next iteration (see, e.g., [37, p. 361]). The results reported here are obtained using five iterations.

The results of applying these techniques to the breast cancer data were shown earlier in Figure 1. Gi and Gs each splits the data once, at progrec ≤ 21 and pnodes ≤ 3, respectively. The corresponding Kaplan-Meier curves in the figure show that progrec is predictive and pnodes is prognostic. The 95% bootstrap confidence intervals of exp(β), the relative risk of hormone therapy versus no therapy, are shown beneath the terminal nodes of the trees. They are constructed as for uncensored response data, with the regression coefficient replacing the mean response. Specifically, let $\mathcal{L}$ and T denote the training sample and the tree constructed from it. Let ${\mathcal{L}}_j^{\ast }$ and $T_j^{\ast }$ denote the corresponding jth bootstrap sample and tree, for j = 1, 2, . . . , J. Let $\widehat{\beta }\left(t\right)$ and ${\widehat{\beta }}_j^{\ast }\left(t^{\ast }\right)$ denote the estimates of in nodes t ∈ T and $t^{\ast }\in T_j^{\ast }$ based on $\mathcal{L}$ and ${\mathcal{L}}_j^{\ast }$, respectively, and let n(A) denote the number of cases in $\mathcal{L}$ that belong to any set A. Define ${\stackrel{‒}{\beta }}_j^{\ast }\left(t\right)={\sum }_{t^{\ast }}n(t\cap t^{\ast }){\widehat{\beta }}_j^{\ast }\left(t^{\ast }\right)∕{\sum }_{t^{\ast }}n(t\cap t^{\ast })$. The bootstrap estimate of the variance of $\widehat{\beta }\left(t\right)$ is the sample variance $s_{\beta }^2\left(t\right)$ of$\{{\stackrel{‒}{\beta }}_1^{\ast }\left(t\right),{\stackrel{‒}{\beta }}_2^{\ast }\left(t\right),\dots ,{\stackrel{‒}{\beta }}_J^{\ast }\left(t\right)\}$ and a 95% bootstrap confidence interval for β(t) is $\widehat{\beta }\left(t\right)\pm 2s_{\beta }\left(t\right)$.

7 Importance scoring and thresholding

When there are many variables, it may be useful or necessary to reduce their number by some form of variable selection. One way to accomplish this is to rank them in their order of importance and select a top-ranked subset. Lack of a proper definition of “importance” has led to many scoring methods being proposed, but few include thresholds for identifying the noise variables. For example, CART and random forest use the information from surrogate splits to compute scores but not thresholds.

Following [38], we score the importance of a variable X in terms of the 1-df chi-squared statistics computed during variable selection. Specifically, let q_t(X) be the value of q(X) (see Algorithms 1 and 2) at node t and n_t be the number of observations in t. We define the importance score of X to be $\mathrm{Imp}\left(X\right)={\sum }_t{n}_t{q}_t\left(X\right)$ and approximate its null distribution with a scaled chi-squared using the Satterthwaite method [39]. This procedure is similar to that in [38] except for two changes. First, the latter employs the weight $\sqrt{n_t}$ instead of n_t in the definition of Imp(X). The new definition increases the probability that the variable selected to split the root node is top-ranked. The other change is in the choice of threshold. In [38], the threshold is the K⁻¹(K − 1)-quantile of the approximating distribution of Imp(X), where K is the number of predictor variables, the motivation being that 1/K of the unimportant variable are expected to be found important. It is difficult to compute the K⁻¹(K − 1)-quantile of the distribution, however, if K is large. Therefore the threshold is defined to be the 0.95-quantile instead. For the breast cancer data, Gi identifies only progrec as important whereas Gs identifies pnodes, progrec, and estrec, in descending order.

8 Application to data with missing values

Missing values pose two problems for tree construction. The first is how to deal with them during split selection and the second is how to send observations with missing values through a split. CART uses a system of surrogate splits that is biased toward choosing variables with few missing values [23, 40]. For variable selection, Gc, Gi, and Gs create a “missing” category in each contingency table. Each split has the form x ∈ S, where the set S may contain the missing values. There is some evidence that this technique is best among classification tree methods if the response variable takes two values [41].

We illustrate the method on a real data set from a retrospective candidate gene study. Owing to confidentiality reasons, the data and solutions are described in general terms here. A total of 1504 subjects were randomized to treatment or placebo and the response is survival time in days, with sixty-three percent censored. The explanatory variables consist of 17 continuous-valued baseline measures (a1, a2, and b01–b15) and 288 categorical variables, of which 6 are baseline measures (c0–c5) and the rest are genetic variables (g001–g282), each having two or three levels. More than 95% (1435/1504) of the subjects have values missing in one or more explanatory variables; only 7 variables (a1, a2, b3, c0, c4, b15, g272) are completely observed.

Although the overall treatment effect is statistically significant (p-value 0.008), its magnitude is small. The question is whether there is a subgroup for which the treatment effect is larger. Owing to the large number of variables, a traditional Cox proportional hazards model is inapplicable without some sort of variable selection, even if restricted to the subset of complete observations.

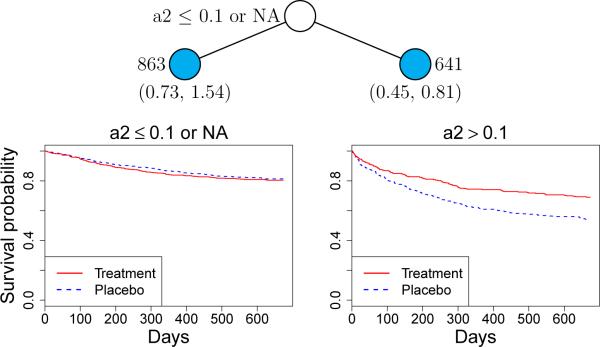
The Gs model, shown in Figure 9, splits only once, on a2. If the latter is less than 0.1 or missing, there is little difference in survival probability between treated and untreated, as shown by the Kaplan-Meier curves below the node. Otherwise, the difference is statistically significant: a 95% bootstrap confidence interval (based on 100 bootstrap iterations) for relative risk (treatment vs. placebo) is (0.45, 0.81). The importance scoring method identifies 27 and 28 important variables for Gi and Gs, respectively. The trees constructed from these variables, however, are unchanged.

Figure 9.

Gs model for gene data. At each node, a case goes to the left child node if and only if the stated condition is satisfied. Sample sizes are beside terminal nodes and 95% bootstrap intervals for relative risk of recurrence for treatment versus placebo are below the nodes.

9 Conclusion

Regression trees are natural for subgroup identification because they find subgroups that are interpretable. But interpretability is advantageous only of the algorithms that produce the trees do not possess selection bias. We have introduced three algorithms that are practically unbiased in this respect. Gc is simplest because it can be implemented with any classification tree algorithm (preferably one without selection bias) by appropriate definition of a class variable. It is limited, however, to binary-value response and treatment variables. Further, some modification of the classification tree algorithm is needed to disallow splits that yield nodes with pure classes.

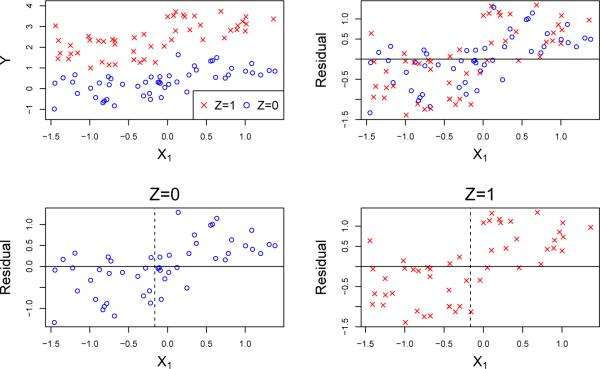
Gs is a direct descendant of the GUIDE regression tree algorithm. As a result, it is more general than Gc, being applicable to any kind of ordinal response variables, including those subject to censoring, to multi-valued treatment variables, and to all types of predictors variables, with or without missing values. If there is no censoring, Gs borrows all the ingredients of GUIDE. The main differences lie in the use of the treatment variable as the sole predictor in a linear model fitted to each node, the construction of a separate chi-squared test of the residuals versus each predictor for each treatment level, and the sum of the Wilson-Hilferty transformed chi-squared statistics to form a single criterion for split variable selection at each node. As the example in Figure 3 demonstrates, however, Gs can be negatively affected by the presence of prognostic variables.

Figure 3.

Plots of data and residuals from the model (4) where X₁ is prognostic

Gi is our preferred solution if the goal is to find subgroups defined by predictive variables only. To avoid being distracted by prognostic variables, Gi uses a chi-squared test of treatment-covariate interaction to select a split variable at each node. It is therefore similar in spirit to the IT method. But unlike the latter, which searches for the split variable and the split point at the same time, Gi uses the chi-squared test for variable selection only. Besides avoiding selection bias, this approach allows missing predictor values and saves much computation time.

We extend Gi and Gs to censored time-to-event data by fitting a tree-structured proportional hazards model to the data using Poisson regression. Poisson residuals are easier to employ for our purposes than those from proportional hazards models. Further, this approach gives a common baseline cumulative hazard function, thereby allowing comparisons of treatment effects between nodes. The price is increased computing time due to the need for iterative updates of the estimated baseline cumulative hazard function, but the expense is not large relative to the other methods, as shown by the average computing times to construct one tree for model M1 in Table 4. (Recall that the predictor variables in M1 take three values each; the speeds of Gc, Gi, and Gs relative to the other methods would be greater if the variables take more values.)

Table 4.

Average times (sec.), over 500 simulation trials of model M1, to construct one tree on a 2.66GHz Intel processor; QUINT does not allow categorical variables

MOB	Gs	Gi	Gc	IT	VT	SI	QU
1.4	4.3	7.0	17.5	127.8	341.1	1601.5	NA

Subgroup identification may be prone to error, especially if the number of predictor variables is large, because the chance of finding the correct variables can be small, as the results for model M1 in Figure 8 show. If the number of variables is large, it is often helpful to eliminate some of the irrelevant variables with importance score thresholds and then construct the trees with the remaining ones. our scoring and thresholding method is particularly convenient for this purpose because, unlike other approaches, it does not require data resampling and hence is much quicker.

To our knowledge, there has not been an effective method of confidence interval construction for the estimates in the nodes of a regression tree. the main difficulty is the numerous levels of selection typically involved in tree construction. not surprisingly, naïve intervals that ignore the variability due to selection are overly optimistic. to solve this problem, we have to account for this extra variability. we do this by using a bootstrap method to estimate the true standard errors of the estimated treatment effects. because each bootstrapped tree is likely different (and different from the original), we do not obtain an interval for each of its nodes. instead, we average the bootstrap treatment effects within each node of the original tree and use the averages to estimate the standard errors of the original treatment effects. we do not yet have theoretical proof of the consistency of this procedure, but the empirical results are promising.

The methods discussed here cannot be expected to provide definitive subgroup identification, because the error rates can be quite high in some situations (e.g., model M1). Of course, it would increase confidence if there is a procedure that can indicate the magnitude of the error rate. Until then, the main utility of the methods is in identifying potential subgroups for scrutiny by domain knowledge experts and validation by independent trials.

Gi and Gs are implemented in the GUIDE computer program which can be obtained from www.stat.wisc.edu/~loh/guide.html.

Algorithm 1 Gs split selection.

1. Fit the least squares model

   $$EY={\beta }_0+\sum _{z=1}^L{\beta }_{z}I(Z=z)$$ (3)

   to the data in the node and compute the residuals. Let S_z denote the set of observations with Z = z in the node.
2. For each X and z = 1, 2, . . . , L.

   • (a)
     Form a contingency table from the data in S_z using the signs (positive vs. non-positive) of the residuals as columns and the (grouped) X values as rows. If X is ordinal, divide its values into two groups at the mean. Otherwise, if X is categorical, let its values define the groups. If there are missing values, add an additional “missing value” row.
   • (b)
     Compute the chi-squared statistic W_z for testing independence, and let _z denote its degrees of freedom. Use (2) to convert W_z to the 1-df chi-squared quantile

     $$r_z\left(X\right)=\max \left(0,{\left[7∕9+\sqrt{{\nu }_z}\left\{{(W_z∕{\nu }_z)}^{1∕3}-1+2∕\left(9{\nu }_z\right)\right\}\right]}^3\right).$$
3. Treating ${\sum }_{z=1}^L{r}_z\left(X\right)$ as a chi-squared variable with L df, use (2) a second time to convert it to a 1-df chi-squared quantile

   $$q\left(X\right)=\max \left(0,{\left[7∕9+\sqrt{L}\left\{{\left(L^{-1}{\sum }_z{r}_z\left(X\right)\right)}^{1∕3}-1+2∕\left(9L\right)\right\}\right]}^3\right).$$
4. Let X* be the variable with the largest value of q(X).

   • (a)
     If X* is ordinal, let A denote the event that X* is missing (if any) andĀ its complement. Then search through the values of c for the split $A\cap \{X^{\ast }\le c\}$ or $\stackrel{‒}{A}\cap \{X^{\ast }\le c\}$ that minimizes the sum of the squared residuals of model (3) fitted to the two child nodes produced by the split.
   • (b)
     If X* is categorical, let g denote its number of categories (including the missing category, if any). If g < 10, search over all (2^g−1 −1) splits of the form X* ∈ S to find the one that minimizes the sum of squared residuals in the two child nodes. If g ≥ 10, limit the search to (g − 1) splits by following a technique in [27, p. 101] for piecewise constant least-squares regression as follows.

     1. Label an observation as belonging to class 1 if it has a positive residual and as class 2 otherwise.
     2. Order the X* values by their proportions of class 1 subjects in the node.
     3. Select the split along the ordered X* values that yields the greatest reduction in the sum of Gini indices.

   If there are no missing X* values in the training data, missing X* in cases to be predicted are imputed with the node mean.

Unlike the basic GUIDE algorithm [19] which divides the values of each ordered X variable into three or four groups in step 2a, we use only two groups here to avoid small cell counts, because each contingency table is constructed from the data for one treatment level only.

The MOB [25] method can be employed similarly, by fitting a linear model as in step 1 of the above algorithm and then using its own permutation-based procedures to select the split variables and split values. Because Gs and MOB are sensitive to both prognostic and predictive variables, however, they may be ineffective if we wish to find subgroups defined by predictive variables only. To see this, suppose now that the data (X₁, X₂, . . . , Y, Z) are generated from the true model

$$Y=2I(Z-1)+I(X_1>0)+\epsilon$$ (4)

with ε independent normal. The simulated data plots in Figure 3 show that Gs and MOB will choose X₁ with high probability even though it is prognostic but not predictive. IT overcomes this by adding the interaction I(Z = 1)I(X > c) to the fitted model and testing for its significance, but this approach requires searching over the values of c, which produces selection bias and may be impractical if Z takes more than two levels. To get around these problems, we instead test for lack of fit of the model

$$EY={\beta }_0+\sum _k{\beta }_{k}I(Z=k)+\sum _j{\gamma }_{j}I(H=j)$$ (5)

where H = X if it is categorical and is the indicator function I(X ≤ x̄) with x̄ being the sample mean of X at the node otherwise. Then we select the most significant X to split the data. Turning an ordinal X into a binary variable may lead to loss of power, but this is compensated by increased sensitivity to interactions of all kinds, including those that cannot be represented by cross-products of indicators, and by allowing missing values in X. We call this the Gi method (“i” for interaction). The procedure is given next.

Algorithm 2 Gi split selection.

1. For each X variable at each node:

   • (a)
     If X is ordinal, divide its values into two groups at its mean. If X is categorical, let its values define the groups. Add a group for missing X values if there are any. Let H denote the factor variable created from the groups.
   • (b)
     Carry out a “pure error” lack-of-fit test (see, e.g., Weisberg [28, Sec. 4.3]) of the model (5) on the data in the node and convert its p-value to a 1 df chi-squared statistic q(X).

2. Let X* be the variable with the largest value of q(X) and use the procedure in Algorithm 1 step 4 to find the split on X* that minimizes the sum of squared residuals of the model $EY=\eta +{\sum }_k{\beta }_{k}I(Z=k)$ fitted to the child nodes.

Applying the method to the data in Figures 2 and 3 yields p-values of 3 × 10⁻¹⁹ and 0.07, respectively.